相干信源的DOA空间谱估计研究

李君惠 杨志强 华 雷

(四川九洲空管科技有限责任公司 四川绵阳 621000)

0 引言

阵列信号处理中的一个重要且常用的领域就是DOA空间谱估计，想要对目标进行超分辨测向，必须计算出信号的空间谱。在实际空间环境中，由于反射遮挡等因素造成了多径干扰，因此存在大量的相干信源。当要进行DOA的信源完全相干的时候，接收数据的协方差矩阵的秩降为一，DOA的信源数就要大于DOA子空间，因此，传统的DOA算法，如MUSIC算法，不能对相干信号源进行分辨测向。DOA算法对相干信源的超分辨测向一直具有研究意义。

1 MUSIC算法原理以及仿真分析

1.1 MUSIC算法原理

当接收信号为窄带时，天线阵列传播期间接收到的信号的包络可以认为是恒定的。阵列天线为线阵时，天线阵列和信源为同一平面内，阵元间距为，接收的信号数目为，信源方向(=1,2,…,)入射根天线，如图1所示。

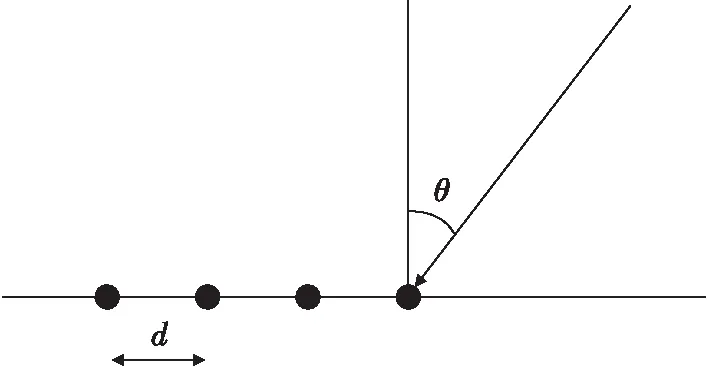
图1 均匀线阵

入射信号向量()为

()=((),(),…())

(1)

线阵响应矢量为

(2)

方向矩阵为

=[(),(),…,()]

(3)

接收到信号为

()=()()+…()()

(4)

实际中存在噪声，阵列接收信号为

()=()+()

(5)

式(5)中，()表示为白噪声向量；()表示为空间信号向量；()表示为接收数据向量；表示为方向矩阵。接收信号的空间相关矩阵可为

=[()()]=+

(6)

对式(6)中的进行特征值分解，其中,,…,为特征值，由此,,…,是对应的特征向量。其中与信号有关的特征值为,,…,，剩下的是与噪声有关的-特征值，综上可以定义噪声子空间表示为

=[+1,+2,…,]

由此，MUSIC的谱估计为

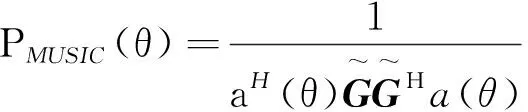
(7)

式(7)中，信号入射方向也就是MUSIC谱函数中的第个峰值相应的位置。

1.2 MUSIC算法仿真分析

利用Matlab仿真软件产生3路信源，并仿真MUSIC算法，仿真参数如表1所示。

表1 实验条件

在表1的条件下，用Matlab仿真给出了MUSIC测向结果，如图2所示。

图2 MUSIC算法仿真

图2(a)仿真采用3路非相干信源，图2(b)仿真采用两个相干信源，方向为-40°和方向为10°。图2的仿真结果可得出结论，MUSIC算法可以有效地对非相干信源进行测向，当信源为相干信源时，MUSIC算法失效。

2 相干算法原理及仿真分析

在处理强相干信源的方法中，主要分为两种：第一种方法采用非降维处理；第二方法采用降维处理。在这些方法中，空间平滑、矢量奇异值类、矩阵分解为降维处理算法；Toeplitz算法、改进MUSIC算法为非降维处理算法。

2.1 空间平滑SS-MUSIC算法原理

为解决相干信源的超分辨测向，提出了只适合于均匀线阵的空间平滑算法(SS-MUSIC)算法。SS-MUSIC算法为了恢复数据协方差矩阵，采用子阵平滑的方法，算法分为：

1)前向平滑MUSIC算法(FSS)；

2)后向平滑MUSIC算法(BSS)；

3)修正的空间平滑MUSIC算法(MSS)。

空间平滑技术是对付强相关信号的有效方法，其算法原理是将均匀线阵(阵元)分成个相互重叠的子阵，其中每一个子阵的阵元数为，因此=+-1，为恢复满秩协方差矩阵，需要求得各子阵协方差矩阵的均值。当相干信源数大于子阵的阵元数目时，前后向平滑数据协方差矩阵均是满秩矩阵。修正的空间平滑算法的实质对前后向平滑矩阵的平均。经过分析可知，FSS算法和BSS算法相比于MSS算法具有更大的孔径损失，同时FSS算法和BSS算法可分辨的信源数相较于MSS算法更少，因此本文只仿真MSS算法。

2.2 改进空间平滑ISS-MUSIC算法原理

在前述基础上进一步做相应的互相关处理，最后对处理后的数据进行加和平均，即得到其等效的空间平滑矩阵。在文献[6]中，作者改进了平滑空间算法，ISS-MUSIC算法首先对信号的协方差矩阵进行修正，然后根据修正后的空间平滑矩阵做波达方向估计计算，ISS-MUSIC算法具有更好的分辨力。

2.3 Toeplitz算法

阵列接收的数据在理想情况下，其协方差矩阵具有Toeplitz性质，然而在实际情况下，接收到的数据会受到误差的影响，尤其是信噪比很低的时候，接收数据的的协方差矩阵通常为对角占优的矩阵。因此要想得到接近真实的数据协方差矩阵可通过对其进行Toeplitz预处理。

Toeplitz算法与矩阵分解算法、空间平滑算法以及矢量重构算法不同，因为该算法的解相干的性能是通过改变协方差矩阵的数据结构获得的，不是由降低自由度而获得，因此，Toeplitz算法具有相对更高的阵列的孔径利用率。由于信号的先验信息没有在算法的数据重构中得到反应，故而当信号源功率不同时，算法的DOA估计精度就会相对不理想，以上分析会在其后的仿真中进一步展示说明。

2.4 矢量奇异值VSV-MUSIC算法

矢量奇异值算法基于定理：阵列接收的数据协方差矩阵特征值分解后，其特征值对应的特征矢量为各信号源导向矢量的一个线性组合，与信号源是否相干并没关系。分析得出，当信号源相干时，其数据的协方差矩阵秩是1，其特征值分解后，只有一个最大特征值，其对应的特征矢量包含所有相干源的信息，因此利用最大特征矢量来解相干。VSV-MUSIC算法需要找出一个矢量，并且这个矢量要含有所有信号源的信息，同样只适用于均匀线阵。

2.5 矩阵分解MD-MUSIC算法

矩阵分解算法的思想和空间平滑相似，只是矩阵分解类算法阵列接收数据的协方差矩阵，对其进行分块分解，然后增广重构。可以证明：理想情况下重构后的矩阵的秩等于信源数。MD算法是针对理想情况下的矩阵重构，与空间平滑技术相似，都是通过降低自由度获得的，同样只适用于均匀线阵。

2.6 相干算法仿真及对比

实验一：两相干源下MSS-MUSIC算法与传统MUSIC算法仿真测向对比。

利用Matlab软件仿真，阵列接收信号为-40°和10°的两个相干信源，仿真条件见表1所示，并进一步给出了MSS-MUSIC算法和传统MUSIC算法的测向结果，如图3所示。

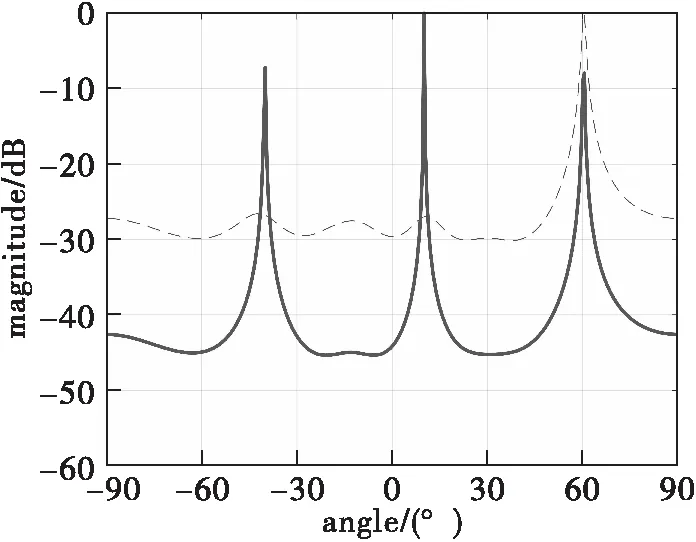
图3 MSS-MUSIC与MUSIC算法仿真(两相干信源)

图3中，虚线表示传统MUSIC仿真结果，实线表示MSS-MUSIC仿真结果，对比可知，当接收信号为相干信源时，传统MUSIC算法不能实现DOA测向，而MSS-MUSIC算法可以实现较好的DOA测向。

实验二：三相干源下MSS-MUSIC算法和ISS-MUSIC的仿真测向对比。

在表1的条件下，-40°、10°以及60°信源采用相干信源，按用Matlab仿真给出了平滑MSS-MUSIC测向结果和ISS-MUSIC测向结果，如图4所示。

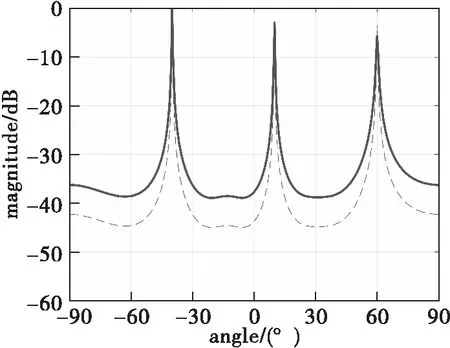
图4 两种平滑MUSIC算法仿真(相干信源)

根据图4对比分析可知，ISS-MUSIC算法形成的谱峰高度要高于MSS-MUSIC算法的谱峰，并且ISS-MUSIC算法的谱峰要比MSS-MUSIC算法的谱峰更尖锐，因此可以认为ISS-MUSIC算法的性能要比MSS-MUSIC优越。

实验三：三相干源下各类相干算法的仿真测向对比。

在表1的条件下，-40°、10°以及60°信源采用相干信源，用Matlab仿真给出了ISS-MUSIC测向结果、Toeplitz算法测向结果、VSV-MUSIC测向结果以及MD_MUSIC测向结果，如图5所示。

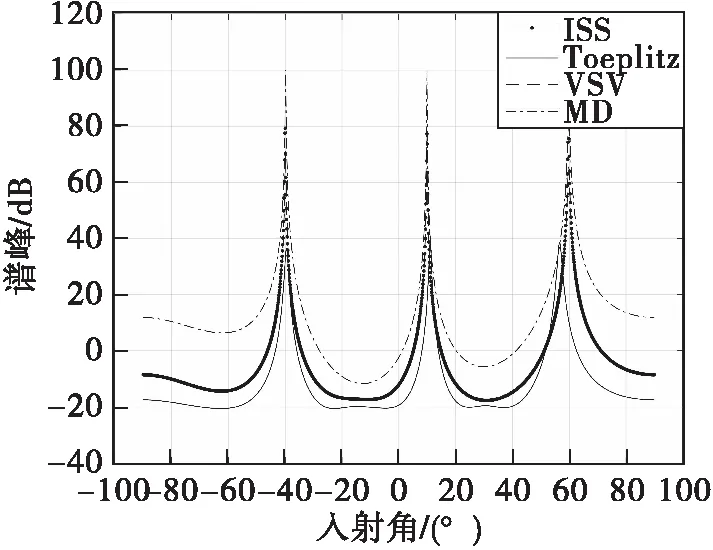
图5 四种平滑MUSIC算法仿真(相干信源)

图5可以看出，在三个相干源时，Toeplitz算法测向精度明显小于其他三种算法，且谱峰的峰值高度也明显低于其他三种算法，因此Toeplitz算法在三个相干源时，效果最差。在ISS-MUSIC、MD-MUSIC以及VSV-MUSIC测向算法中，MD-MUSIC谱峰值略高于ISS-MUSIC和VSV-MUSIC，图5可知ISS-MUSIC和VSV-MUSIC曲线几乎重合，测向精度三种算法大体相当，因此进一步分析在不同信噪比情况下的性能。

实验四：三相干源下各类相干算法的RMSE对比。

在表1的条件下，信噪比为-10dB到10dB。Matlab仿真给出了ISS-MUSIC测向结果、Toeplitz算法测向结果、VSV-MUSIC测向结果以及MD_MUSIC测向结果，如图5所示。

图6可以看出，在不同信噪比的情况下，Toeplitz算法的测向精度最高，且有相对较高的谱峰高度，其次是VSV-MUSIC和MD-MUSIC算法，其他的误差较大。因此在低信噪比下，Toeplitz算法最优。

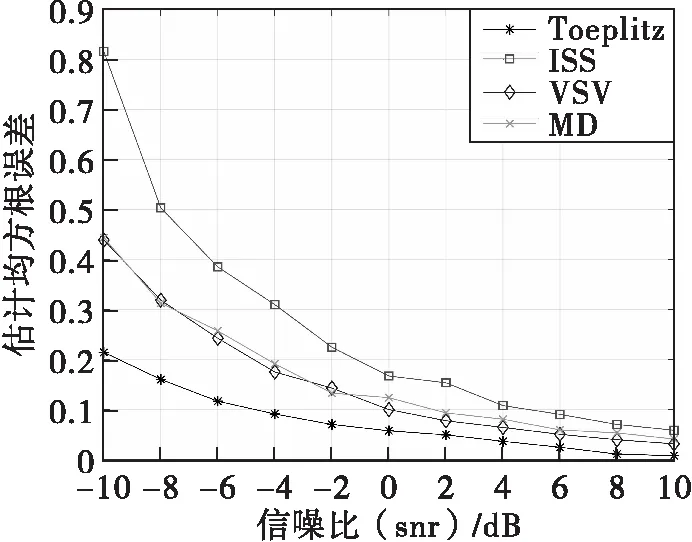
图6 四种滑MUSIC算法仿真(低信噪比)

3 结束语

根据以上分析，对八元超分辨给出以下建议：

1)若实际情况中，要估计三个相关源，且信噪比较高，优先选择VSV-MUSIC算法，其次是ISS-MUSIC算法以及MD-MUSIC算法。

2)若实际情况中，信噪比较低，且对分辨力和估计误差要求不高，应该选择Toeplitz算法。