基于助学案的融合课堂初探——以数学实验课皮克定理为例

◎张文珠 （无锡市新区第一实验学校，江苏 无锡 214000）

本节课是为苏科版《数学》七年级下册而设计的一节数学专题课.在授课形式上，本节课属于数学实验课.实验探究是学生积累数学基本活动经验的重要方式，也为同伴互助式课堂提供了很好的实验平台.在课时内容上，本节课选择的是格点问题.格点问题有助于学生理解基础知识，并且能够在提高学生基本技能的同时逐步培养学生的运算能力、空间想象能力、逻辑推理能力，以及学生的数学核心素养.课时内容打破了学科界限，融入了地理、美术等学科内容，达到了课程育人的目的.在学习形式上，采用的是基于助学案的同伴互助学习方式，发挥教师的主导作用，发挥学生的主体作用.这种学习方式可达到学习者个人和同伴的共同提高.下面，以数学实验课皮克定理为例，结合相关教学片段谈谈作者自己的认识.

学情分析：学生在小学阶段经常会使用钉子图或方格纸，进入初中阶段，在苏科版《数学》七年级上册《6.4 平行》《6.5 垂直》中也使用方格纸进行了平行线和垂线唯一性的探索，已经初步具有工具意识和数形结合思想.对于多边形面积的求法，无论是公式法还是割补法，学生已经有了一定的知识储备.这些，就是开展本节数学实验课的基础.

一、基于课型，“两案”相融，合二为一

初中阶段的数学实验有两类：实际操作型实验和逻辑推理型实验.实际操作型实验就是学生利用一些纸片、木棒、测量工具、计算机等实物进行量、折、拼等活动，经历观察、实验、猜想、证明、归纳等数学活动，获得数学知识和解决问题的方法.逻辑推理型实验就是学生不借助于实物工具，而是运用模拟、类比、联想等方法进行逻辑推理，以获得正确实验结果.数学实验既可以是教学片段，也可以设计成专题实验课.本课时属于实际操作型专题数学实验课.

课前设计时，根据本课时内容和课时类型，制定的是同伴互助型学习方式，并制作了“两案”：助学案和实验报告.本课时助学案的设计理念是“基于理解的逆向设计”，就是教师在考虑如何开展教与学活动之前，先努力思考学习要达到的目的到底是什么，以及哪些证据表明学习达到了目的，也就是“以终为始”，从学习结果开始逆向思考.助学案的这种设计理念，旨在促使学生参与探究活动，提升学习迁移能力，为学生提供理解的框架，帮助他们理解一些零散的知识，并揭示与内容相关的大概念.这种设计方式，对我们的教学研究从经验型转向实证型，对教学从知识为本转向核心素养为本，都是具有实际操作性和借鉴意义的.基于皮克定理是一节专题数学实验课，实验报告的设计与书写也是其重要组成部分.它不仅记录了学生的实验过程，也是学生学习过程的信息反馈.教师可以通过实验报告的反馈，了解教与学过程中的问题，及时解决问题.而实验报告的书写，也是学生在学习过程中需要掌握的一项重要的基本技能.它不仅仅是记录实验的过程，更重要的是它可以初步地培养和训练学生的逻辑归纳能力、综合分析能力和文字表达能力.

在课时设计时，发现“两案”有很多地方是相辅相成的，于是将“两案”合一，将实验报告融入助学案，给学生提供一个完整的实验过程（见表1）.

表1 “两案”合一的助学案设计

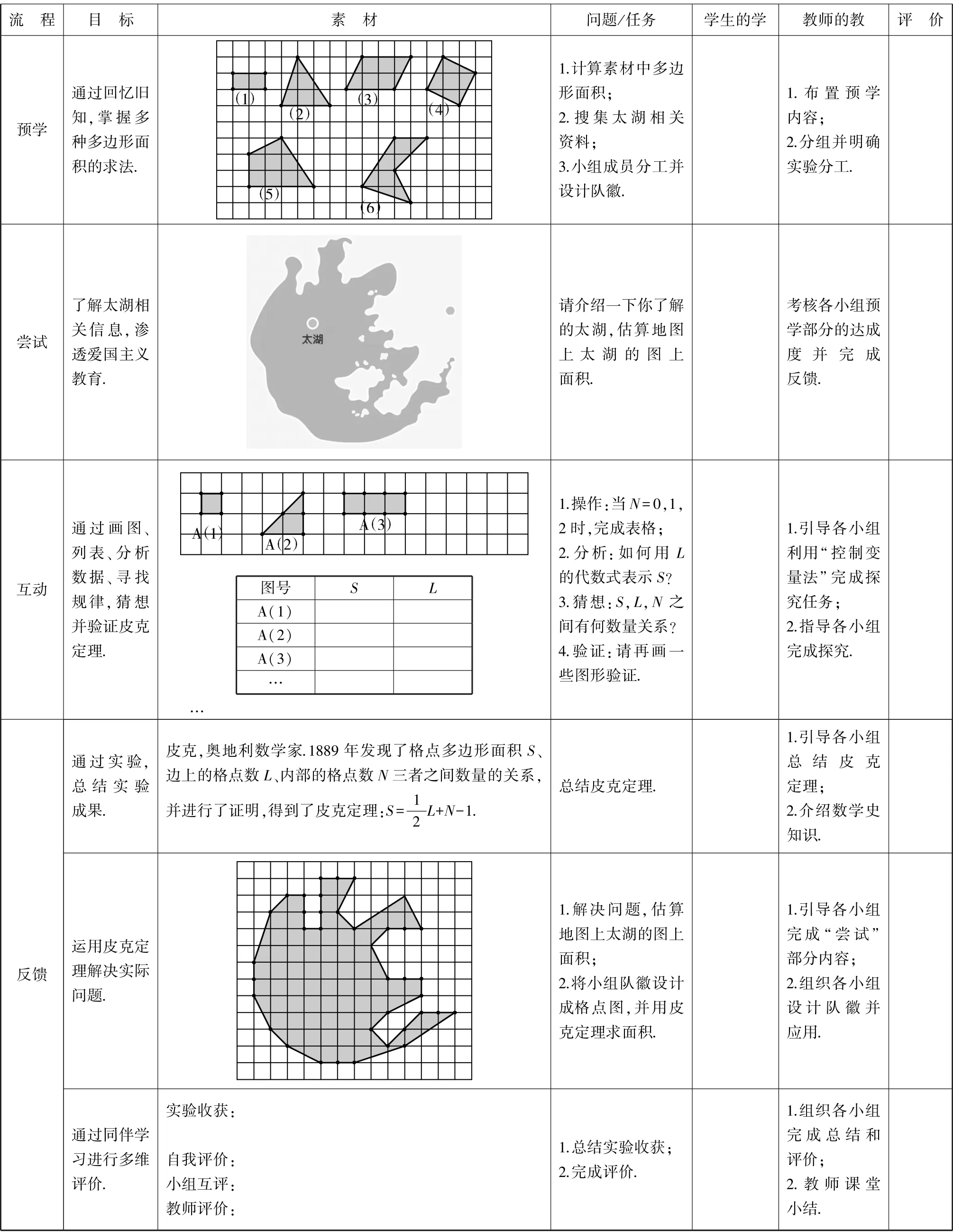
续 表

助学式实验报告由“预学、尝试、互动、反馈”四个助学环节构成，渗透“基于理解的逆向设计”理念，设计中“教、学、评”统一，让学生循序渐进展开互助学习.为了实验课能高效开展，实验报告在“预学”环节设计了三个任务：一是计算格点多边形的面积，让学生经历一个从“数格子”到“特殊多边形的面积公式”再到“割补法”的运用过程，从而达到知识唤醒的目的，为皮克定理提供探究基础.二是搜集太湖的相关资料，让学生在搜集资料的过程中增加相关地理知识，感受祖国大好河山的壮丽.三是进行小组分工，明确职责，设计队徽.小组队徽的设计也增加了小组的团队合作意识和凝聚力，为实验的开展做好了充分的准备工作.“尝试”环节设计是介绍太湖，估算地图上太湖的图上面积，让学生感受到已有知识和能力不足以解决这个实际问题，目的是让学生遇挫，从而顺利引入新知的探究.在“互动”环节设计完整的实验过程，探索和验证皮克定理的具体内容.这一环节，充分体现了学生的主体地位，教师以一个组织者、引导者与合作者的身份参与探究，引导学生经历一个“画图—列表—分析数据—寻找规律—猜想—验证”的过程，渗透“特殊到一般、变量控制、分类讨论、符号意识”等数学方法和素养.“反馈”环节设计了总结实验成果、新知应用、多维评价三个内容.小组在队徽的设计、计算面积的拓展活动中，充分发挥同伴互助的学习优势，最终解决问题.在助学式实验报告中，不仅有完整的实验过程，而且有一个完整的学习应用过程，让学生在实验中收获的不仅是数学知识，还有教师隐性的数学方法的指导、数学核心素养的培养.

二、基于学案，多维相融，实现课程育人

1.立足学科，以融合强学科

融合理念下的课程实施是以“学科知识＋”为基本形态的，这就是要打破学科局限，进行多学科融合，通过不同学科之间的融合生成对本学科新的认识，促进数学学科走向立体.无锡，位于太湖之滨，被称为“太湖明珠”，自古就是鱼米之乡，是吴文化的发源地.在助学案“尝试”板块中以此架构文化背景渗透爱国主义教育，在历史、地理知识的融合下，设计“估算地图上太湖的图上面积”的数学问题，将问题置于情境中.皮克定理是基于格点作图展开的探究，因此将生活中的图形、创作的图形设计成格点图解决问题是本节课的难点.这一过程又融合了学生的审美、创作、绘画能力，将美术课程的精髓融入了数学课堂.学科的融合，让有价值的知识打破学科界限，创生出新的领域或者对数学学科产生新的认识，促进数学学科走向丰盈，让学生在整体上把握知识的来龙去脉.

2.立足经验，以融合促经验

在学生参与的数学活动中，学生解决由生活走向课堂的、由学生结合自己经验设计的问题，获得的活动经验更加深刻，更有意义，融合度更高.以本课时为例，在助学案“反馈”板块中，要求学习小组将自主设计的队徽转换为格点图，并用所学皮克定理的知识计算队徽面积，是一个开放性问题.学生设计的队徽涉及体育、动物、工具、英文字母等.学生在解决问题的过程中，他们会综合课内课外、自身所学的知识，这样融合的不仅涵盖学科知识、生活常识，还有同学之间不同的技能（画画、创作、审美）等.除了这些显性的技能，一些隐性的经验也不可忽略.这节数学实验课，教师立足学生主体活动经验，带领学生经历了一个完整的解决问题的过程，让学生积累了解决问题的经验，学生在参与观察、实验、猜想、证明等数学活动中，清晰地表达自己的想法，发展了合情推理和演绎推理的能力.

3.立足育人，以融合铸素养

数学学科的教学不仅承载着传递数学知识、培养数学能力的重任，还肩负着数学育人的重任.这需要通过学科间、校内外、个体与社会之间的广泛融合，促进学生素养的培养，达到育人的最终目的.育人的最终指向要求学生关注生活现实，通过教师采取的真实任务驱动，实现学生素养的提升，这是融合理念下的融合课堂典型的共性特征.本课时中，太湖图上面积的估算以及小组队徽的设计和计算，都是源于现实世界的真实问题、真实需求，基于学科知识的融合，基于活动经验的融合，基于社会需求的融合.“数形结合、特殊到一般、符号意识”等数学思想方法的应用，为学生解决问题提供了专业的知识、技能和方法，在学生解决问题的过程中其素养也得到了提升.这是基于社会需求的融合，是立足社会发展的需求.

三、基于课堂，同伴学习，实现能力提升

融合课堂，不仅是学科与学科、经验与技能、方法和素养、学习与生活的融合，还是一个学生共学、共促、共享、共创、共赢的主阵地.在课堂上，学生发现问题、提出问题、分析问题、解决问题.在这个过程中，学生学会了尊重、合作与分享.本课时从课前的小组分工、资料搜集开始，学生就进入了一个团队角色扮演，这个团队有组织、有任务.在小组探究过程中，成员能力的参差不齐也给同伴互助学习创造了契机，从而取长补短，共克难关.皮克定理的探究过程有两个难点：一是学生在设计图形时，画出的图形不能满足内部点数的要求，得出数据直接影响实验结果.通过小组同伴互助学习，总结出的活动经验是先确定图形内部的点，然后根据点的位置来设计格点图形更方便.二是寻找，，之间的关系，小组内同学会有不同的结论，此时同伴之间可根据实验数据互相纠错，讨论并订正，直至找到正确的数量关系.这些活动经验的得出、问题的解决就是同伴互助学习的成果.

融合课堂重点关注的是综合所学解决实际问题，培养学生自主探究等超越学科的综合能力与品格.这样设计，学生由于亲自动手操作，从一个旁观者和听众变成了一个参与者，因此更容易对实验结果、产生结果的原因、新的知识以及新的方法等产生强烈的好奇心.在这种内驱力的推动下，他们会主动寻求同伴的帮助，并将自己的实验结果和同伴分享，在分享过程中不断完善实验过程和结论，达到一个共同进步的双赢状态.而这些，就是作为引导者的教师最期望看见的.