薄壁加劲钢管抗震性能有限元分析
祖庆芝,李 俊
(1.漳州职业技术学院建筑工程学院,福建 漳州 363000;2.四川轻化工大学土木工程学院,四川 自贡 643000)
引 言
在可再生能源技术中,风力发电机的使用呈指数级增长,以满足不断增长的电力需求。随着风力发电机设计和发电能力的不断增长,各种风电塔屈曲倒塌工程问题也逐渐暴露出来[1-3]。风电塔支撑结构作为典型的薄壁高耸结构,在地震及大风等突发荷载作用下极易发生屈曲,造成风电塔屈曲倒塌破坏,如图1所示。

图1 风电塔屈曲倒塌破坏
《钢结构设计标准》[4]13.1.2 条规定,圆钢管的外径与壁厚之比不应超过100ε2Κ(εΚ为钢号修正系数),该径厚比限值的设定范围较宽;《建筑抗震设计规范》[5]8.4.1条规定,在抗震等级为一级、二级、三级、四级时,对应的圆管外径与径厚比限值分别为38×(235/fay)、40×(235/fay)、40×(235/fay)、42×(235/fay),其中fay为消能梁段钢材的屈服强度。但实际工程中,作为主要承重结构的圆钢管结构,为满足大型钢材需求,外径与壁厚之比通常会超过100ε2Κ,这种情况下圆钢管结构的抗震性能存在诸多不确定性。对于较大径厚比钢管结构,日本道路协会[6]提出圆钢管或矩形钢管结构应设置内部加劲肋,以达到提高结构韧性的目的。同时,国内外也有诸多学者开展了这方面的研究。李海锋等[7]针对设置耗能壳板的新型高强钢圆管桥墩的受力机理进行了研究,发现设置耗能部件的结构,在轴向荷载作用下其承载能力和延性均有一定程度的提高。张丽娟等[8]对有/无环形加劲肋的输电塔节点缩尺模型进行了承载力对比试验研究,分析了环形加劲肋对该类节点屈服承载力和极限承载力的影响。王俊亮[9]研究了不同径厚比及长细比情况下圆钢管结构的滞回性能,对薄壁圆钢管桥墩的损伤滞回模型进行了相应修正。径厚比大的圆钢管结构在荷载作用下最易发生屈曲破坏。为了探究大径厚比圆钢管屈曲破坏形式及解决措施,牛奔[10]进行了大径厚比圆钢管的加劲肋试验,但试验只采用了传统的单调加载方式,并未研究在循环荷载作用下圆钢管结构的破坏形式,对于加劲肋横截面类型而言仅研究了一字型和槽型两种类型。Zhang 等[11]研究了考虑受压屈曲的圆钢管构件参数滞回模型。Kang 等[12]研究了可作为风力机支撑塔结构的大直径圆柱壳开孔对结构稳定性和极限强度的影响,分析了开孔周围一圈加劲肋厚度对结构极限强度的影响,提出了确定大直径圆柱壳圈加劲肋厚度的有效公式。Florent等[13]针对航空航天工业中出现的大型加劲圆柱壳结构,提出了一种新的加劲肋布置优化方式。小野潔及岡田誠司等[14-15]分别对圆形及矩形受轴压力钢管进行了拟静力试验,分析了不同壁厚及不同横截面类型的钢管结构的抗震性能,但所研究的钢管结构径厚比均为57,实验结论无法反映更大径厚比钢管结构的抗震性能。鉴于目前对于不同径厚比圆钢管结构加劲肋横截面类型的研究较为欠缺,相关规范也没有给出明确的类型选择,本文选取3 种不同径厚比圆钢管结构及3 种不同横截面类型的加劲肋,通过有限元软件ABAQUS 开展低周往复加载数值模拟,研究不同横截面类型的加劲肋对圆钢管结构刚度、延性和抗震性能等指标的影响规律。
1 结构选型与有限元模型建立
1.1 结构形式选择
选取外径均为500 mm,壁厚分别为10.0 mm、6.7 mm 和5.0 mm(ϕ500 × 10.0、ϕ500 × 6.7、ϕ500 ×5.0)的3 种圆钢管结构(径厚比分别为50、75 和100),结构高度均为1500 mm。每种圆钢管结构均分别设置槽型、半圆型和三角型3 种横截面类型加劲肋,加劲肋间隔成60°均匀分布。加劲肋横截面类型及几何尺寸如图2 所示,图中尺寸单位均为mm。圆钢管结构编号及参数见表1。
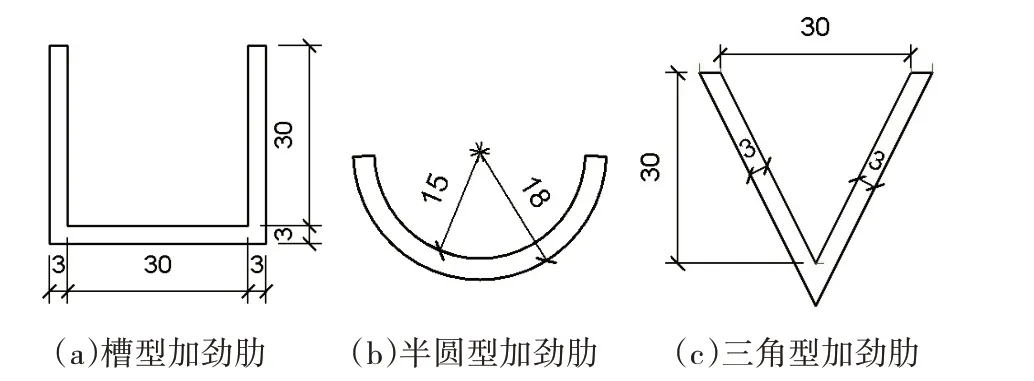
图2 加劲肋横截面类型及几何尺寸
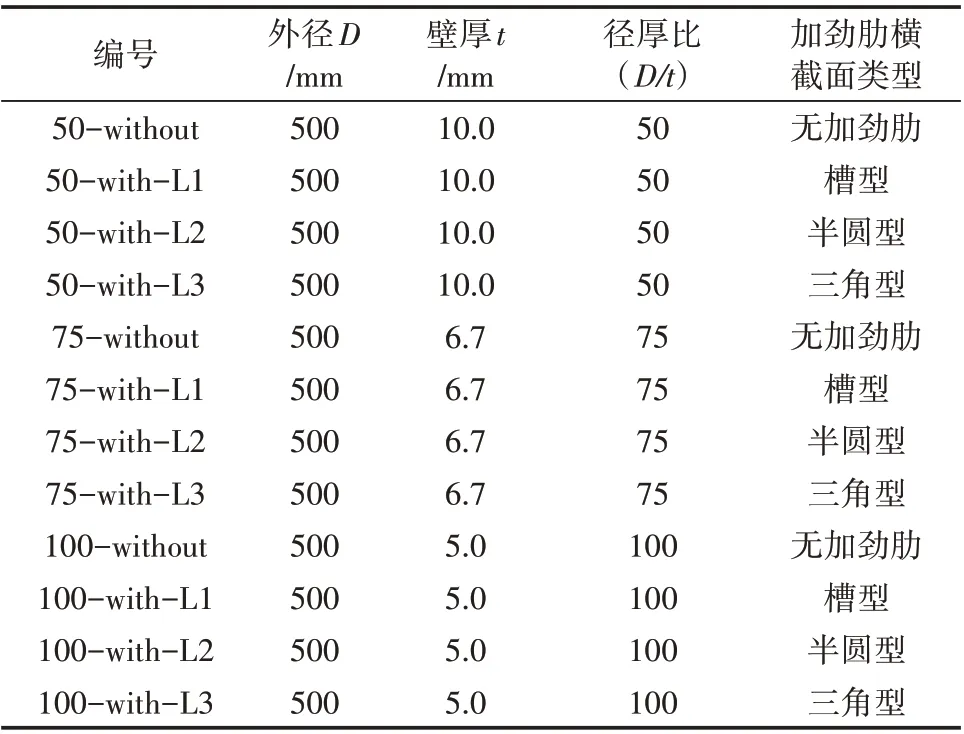
表1 圆钢管结构编号及参数
1.2 加载制度的确定
拟静力实验加载制度参照文献[5]及《建筑抗震试验规程》JGJ/T101-2015[16]确定,其中结构侧向屈服位移Δy按照式(1)~(2)计算:
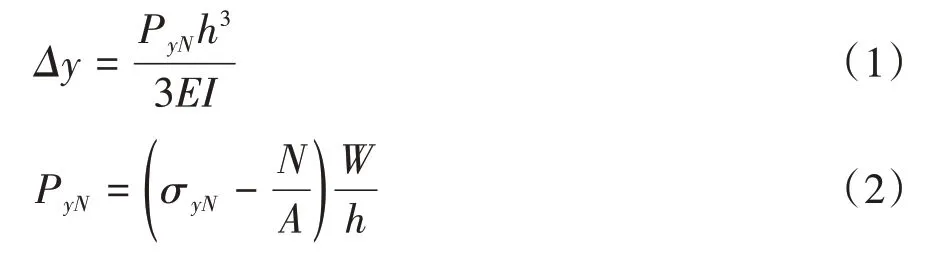
式中:Δy为结构侧向屈服位移,m;PyN为结构侧向屈服力,N;h为水平荷载作用高度,m;E为弹性模量,Pa;I为断面极惯性矩,m4;σyN材料屈服强度,Pa;N为轴向作用力,N;A为截面面积,m2;W为断面系数,m3。
侧向屈服位移计算结果见表2。
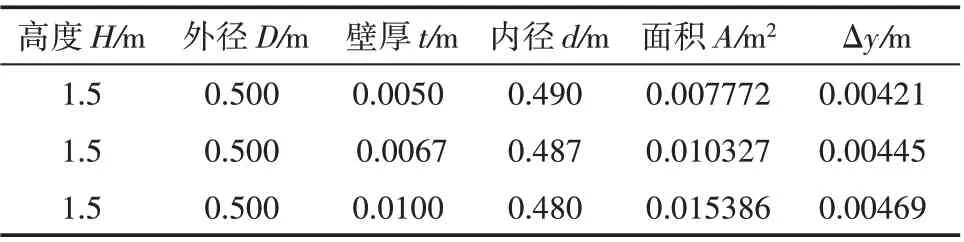
表2 结构尺寸及对应侧向屈服位移
如图3 所示,首先施加500 kN 的垂直向下的轴压力,采用位移控制的方式进行横向加载,结构屈服前以0.1Δy为增量进行逐级递增加载,屈服后采用整数倍Δy进行循环加载,加载到10Δy结束。加载幅值曲线,如图4所示。
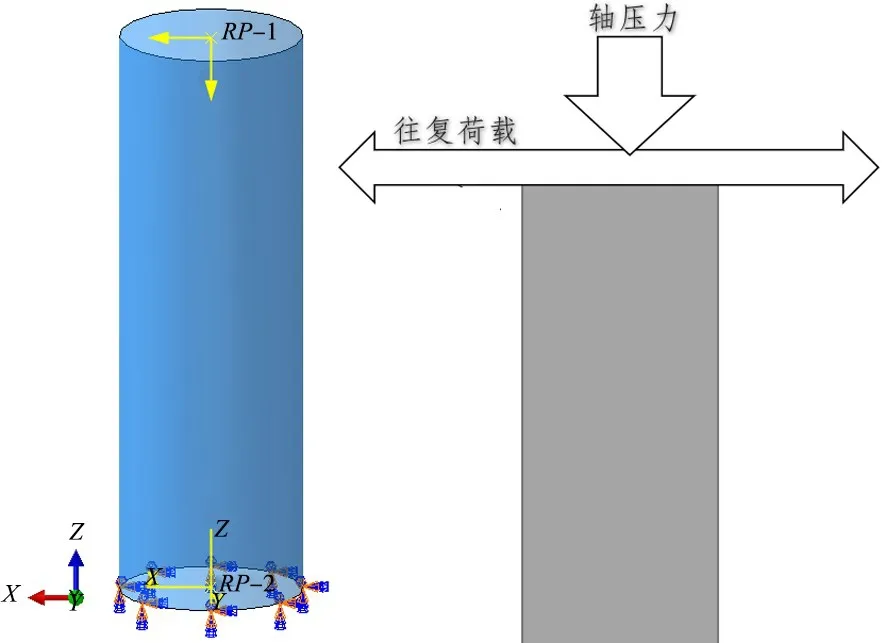
图3 加载方式
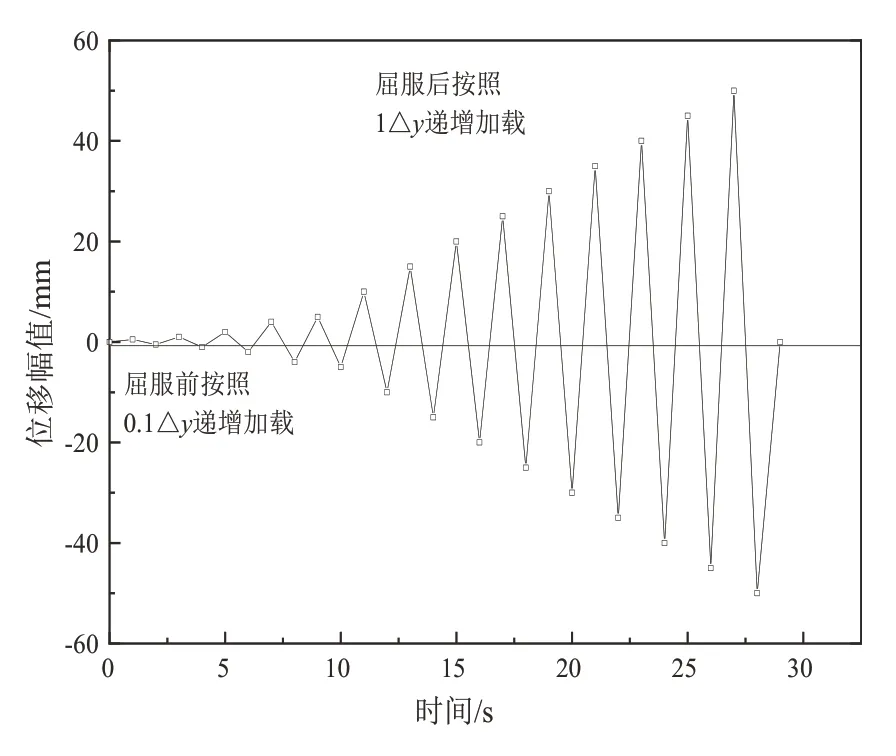
图4 加载幅值曲线
1.3 有限元分析模型的建立
利用有限元分析软件ABAQUS 建立不同壁厚圆钢筒模型,节点总数为6005,单元总数为5925,材料本构关系参考王萌[17-18]及王元清等[19]所做的Q345B 钢材在循环荷载作用下的应力-应变关系,如图5 所示。参考庄茁在《ABAQUS 非线性有限元分析与实例》[20]所介绍的方法计算出钢材的真实应力-真实塑性应变关系,利用有限元分析软件ABAQUS 中的Combined 模块输入Q345B 钢材本构参数(表3);单元类型选用S4R 壳单元,单元节点数目为4,厚度定义为构件壁厚。
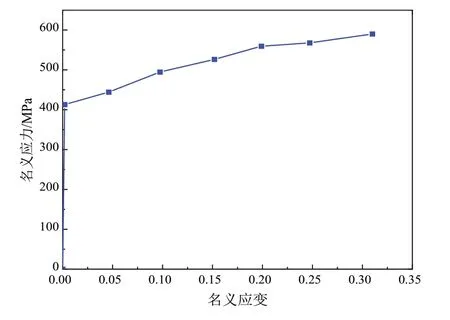
图5 Q345B钢材本构关系
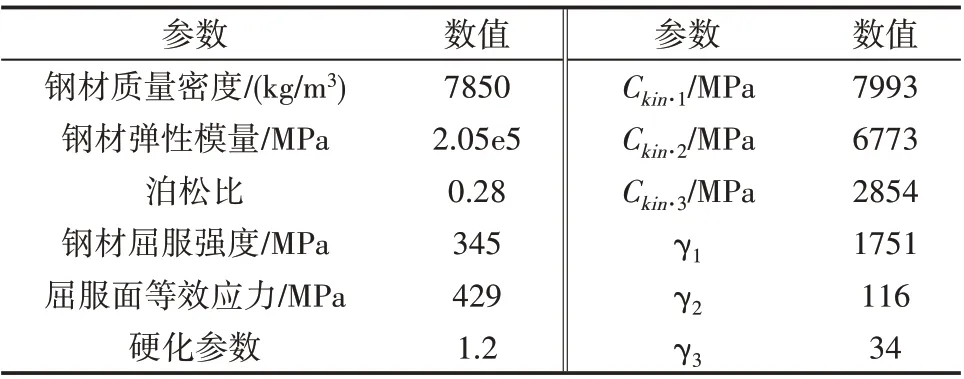
表3 Q345B钢材本构参数[17-19]
2 不同横截面类型加劲肋对圆钢管结构抗震性能的影响分析
为保证模拟结果的合理性,在建立上述模型的同时,参考小野潔[14]所做实验,建立外径400 mm、壁厚9 mm 的圆钢管构件有限元分析模型,按照文献[14]中实验加载方式进行有限元分析,实验和模拟结果如图6 所示。由图6(c)可知,模拟所得到的结构变形与文献[14]中实验得到的结构变形一致,均为“象足式屈曲”。从反力-位移曲线可以看出,模拟所得最大反力为355 N,屈服位移为25 mm;实验中结构最大反力为358 N,屈服位移为26 mm,可见模拟结果与实验结果吻合较好,数值模拟可以保证计算的合理性。
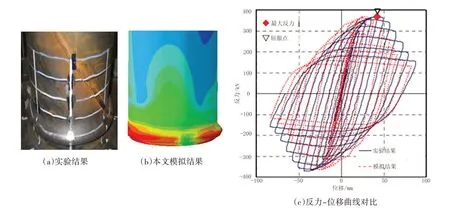
图6 实验与模拟结果对比
提取外径为500 mm、壁厚为10 mm 的设置横截面类型为槽型、半圆型和三角型加劲肋的不同圆钢管结构加载点反力-位移滞回曲线及相应Mises 应力云图,如图7所示。
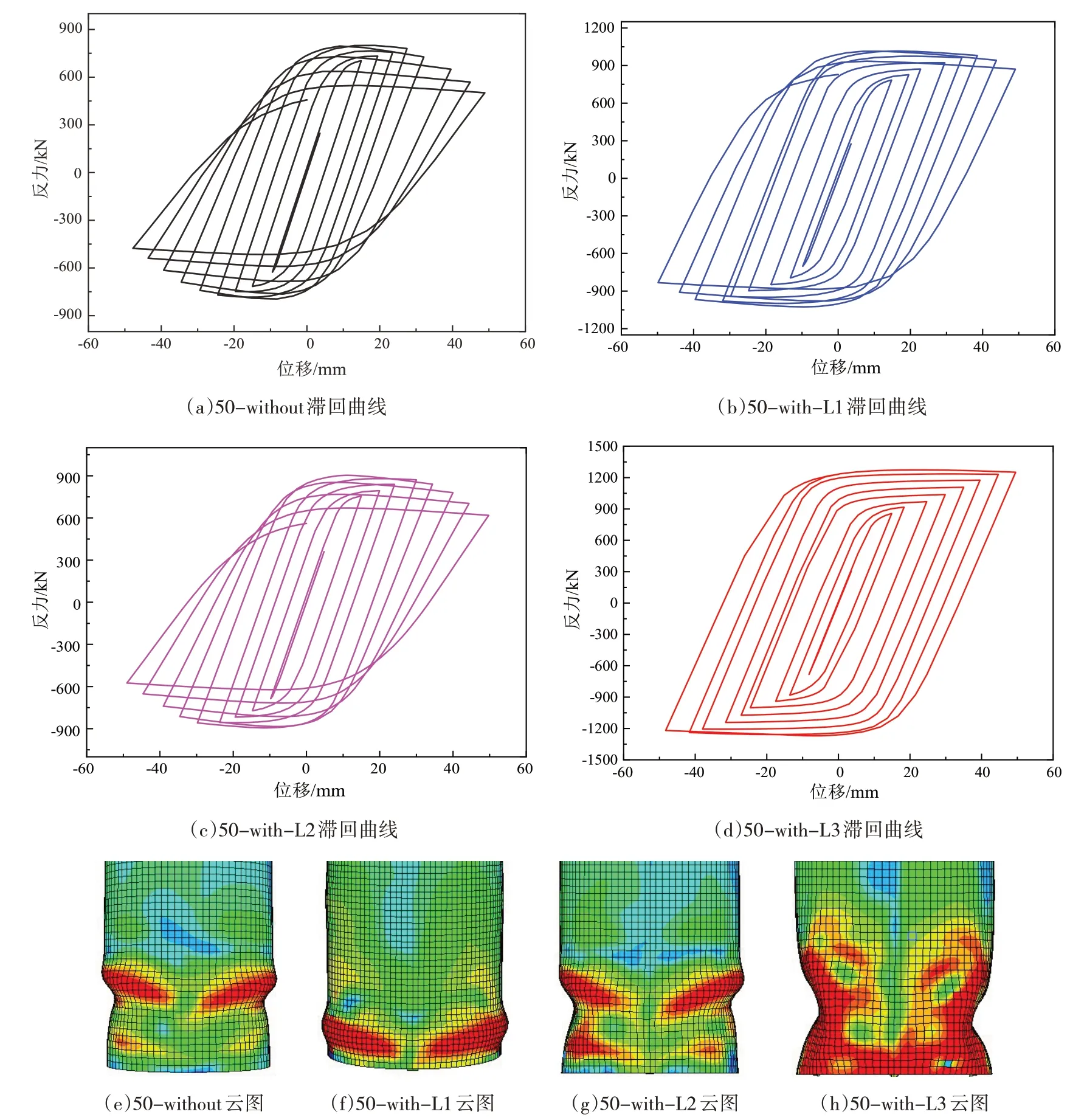
图7 结构反力-位移滞回曲线及Mises应力云图
由图7(a)可以看出,当径厚比为50 时,无加劲肋的结构最大反力为800 kN,最大反力对应的最大位移为27 mm,等于5.5Δy,当位移达到35 mm 时,结构反力下降到最大反力的85%;从图7(e)所示的Mises 应力云图可以看出,在距离结构底部300 mm处出现明显的“凹凸屈曲”,由于存在剪切效应,屈曲呈现非对称现象。
由图7(b)可以看出,设置槽型加劲肋的径厚比为50的圆钢管结构最大反力为1000 kN,最大反力对应的最大位移为38 mm,等于7.6Δy,当位移达到48 mm时,结构反力下降到最大反力的85%;从图7(f)所示的Mises应力云图可以看出,结构屈曲位置发生明显变化,屈曲部位距离底部100 mm,且仅出现“凸起屈曲”,屈曲较为对称,没有明显的剪切效应影响。
由图7(c)可以看出,设置半圆型加劲肋的径厚比为50的圆钢管结构最大反力为900 kN,最大反力对应的最大位移为30 mm,等于6Δy,当位移达到38 mm 时,结构反力下降到最大反力的85%,即结构发生破坏;从图7(g)所示的Mises 应力云图可以看出,结构屈曲位置与不设置加劲肋近似,在距离底部300 mm处出现屈曲。
由图7(d)可以看出,设置三角型加劲肋的径厚比为50 的圆钢管结构结构最大反力为1200 kN,在加载至10Δy时结构仍未发生破坏;从图7(h)所示的Mises应力云图可以看出,结构没有明显屈曲变形。
同理分析分别设置槽型、半圆形和三角型加劲肋的径厚比为75 及100 的圆钢管结构,并将其最大反力、破坏位移、屈曲形式及位置列入表4中。根据图7 及表4 可知,当圆钢管结构径厚比逐渐变大时,结构的屈曲形式由“凹凸双向屈曲”变为“仅凸出屈曲”。设置加劲肋可以有效提高结构最大反力,且从最大反力来看,三角型加劲肋优于槽型加劲肋,同时槽型加劲肋优于半圆型加劲肋,即三角型加劲肋可以为结构提供更高的承载力。由屈曲位置的变化可以看出:设置加劲肋的结构,其屈曲位置发生了明显变化;没有设置加劲肋的结构在往复荷载作用下形成屈曲铰,通过屈曲铰消耗输入的能量,但是在设置加劲肋后,结构屈曲区域变大,但未形成屈曲铰耗能,通过屈曲区域的扩展和材料的不断失效消耗外部的能量输入。
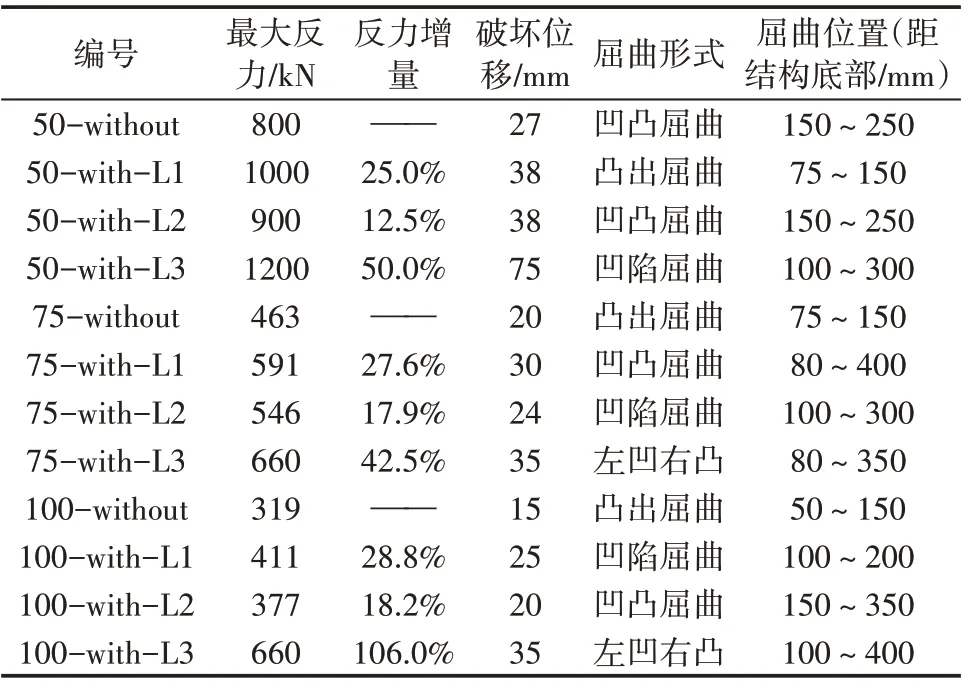
表4 不同结构反力及屈曲对比
3 结构刚度退化及延性分析
3.1 结构反力-位移骨架曲线及刚度计算
将结构反力-位移(F-Δ)滞回曲线各滞回环峰值反力及位移点相连,可得到不同结构的F-Δ 骨架曲线如图8所示。
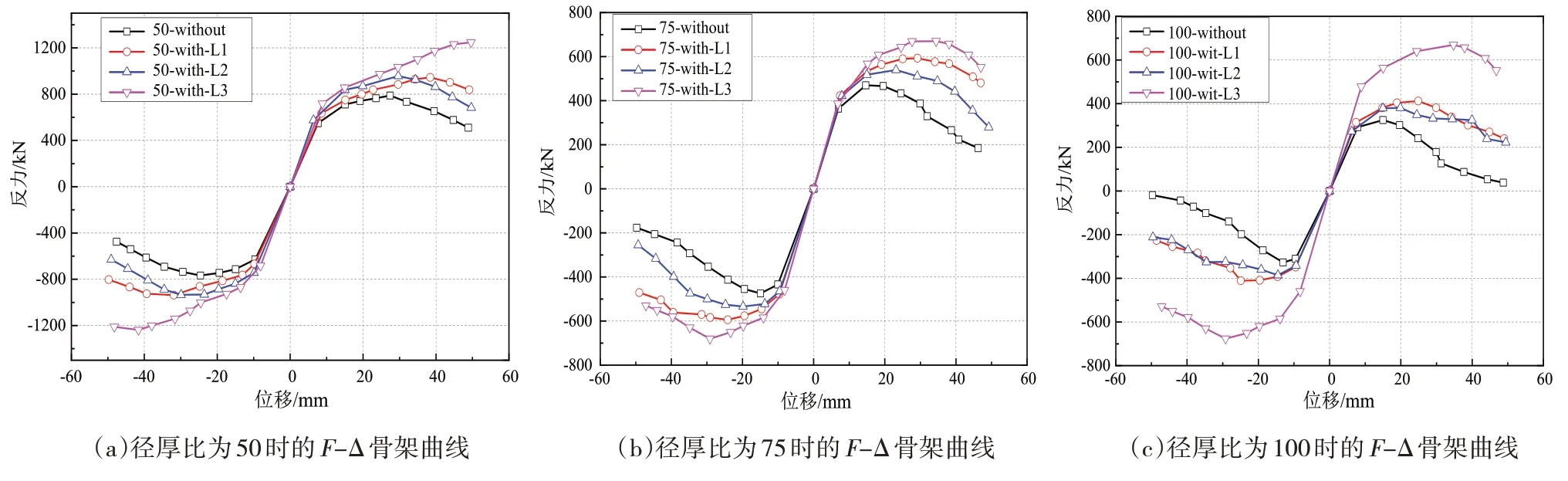
图8 不同结构的F-Δ骨架曲线
在轴压力及往复荷载作用下,结构出现屈曲破坏,导致结构反力及刚度变化;结构的屈曲不仅导致结构承载力下降,还导致结构刚度变为负值。从图8中可以看出,在往复荷载作用下,各种结构均经历了弹性、弹塑性及塑性破坏3 个阶段。在弹性阶段,F-Δ 骨架曲线均呈线性关系。随着位移幅值的增大,F-Δ 骨架曲线出现转折,结构刚度开始下降,构件屈服并逐渐进入弹塑性阶段。当位移继续增大,结构刚度不断减小,当水平荷载达到最大值后,曲线开始下降,刚度变为负值,直至结构破坏。
此外,从图8中可以看出,不同结构的F-Δ骨架曲线之间均有分离,说明设置加劲肋不仅引起结构初始刚度变化还会引起结构水平反力的明显增大。从耗能角度看,设置加劲肋的结构,更大区域的材料参与到受力及耗能中,耗能能力更强;同时,加劲肋的存在增强了结构协同受力的能力,提高了材料的利用效率。
《建筑抗震试验规程》JGJ/T101-2015[16]4.5.3 条规定,试件的刚度可用割线刚度Ki来表示,割线刚度Ki按式(3)计算:

式中:+Fi为第i次循环时推向峰值点的荷载值;-Fi为第i次循环时拉向峰值点的荷载值;+Δi为第i次循环时推向峰值点的位移值;-Δi为第i次循环时拉向峰值点的位移值。
退化程度可用各位移级的割线刚度与初始弹性刚度的比值来表示。不同结构的结构刚度退化曲线如图9所示。

图9 不同结构的结构刚度退化曲线
由图9所示的不同结构的结构刚度退化曲线可以看出,不同结构的刚度退化规律趋于一致。加载初期,结构处于弹性阶段,刚度基本保持不变;加载至屈服位移后,结构刚度出现显著退化,在5Δy后,退化降幅开始逐渐降低,其原因在于加载至5Δy后结构出现塑性铰,且塑性铰随载荷增加逐渐发展,结构耗能主要由塑性铰承担。从不同结构的结构刚度退化曲线可知,三角型加劲肋的刚度在加载任意时刻均大于其他两种类型加劲肋,由于三角型加劲肋使结构塑性铰范围扩大,因此进入塑性阶段后,结构的刚度下降速度更低。
3.2 不同加劲肋对圆钢管结构延性影响
延性系数通常用来描述结构抗震性能,延性系数越大说明结构安全储备越大。《建筑抗震试验规程》JGJ/T101-2015[16]第4.5.1 条规定,破坏荷载及极限变形应取试体在荷载下降至最大荷载的85%时的荷载和相应变形。《建筑抗震试验规程》JGJ/T101-2015[16]第4.5.4 条规定,试件的延性系数μ应按照式(4)计算:

式中:μ为延性系数;Δu为结构的破坏位移。
通过图8所示的不同结构的F-Δ骨架曲线求出不同结构的破坏位移,并按照式(4)计算出不同壁厚结构的延性系数。不同工况下所对应的结构破坏位移及延性系数,见表5。
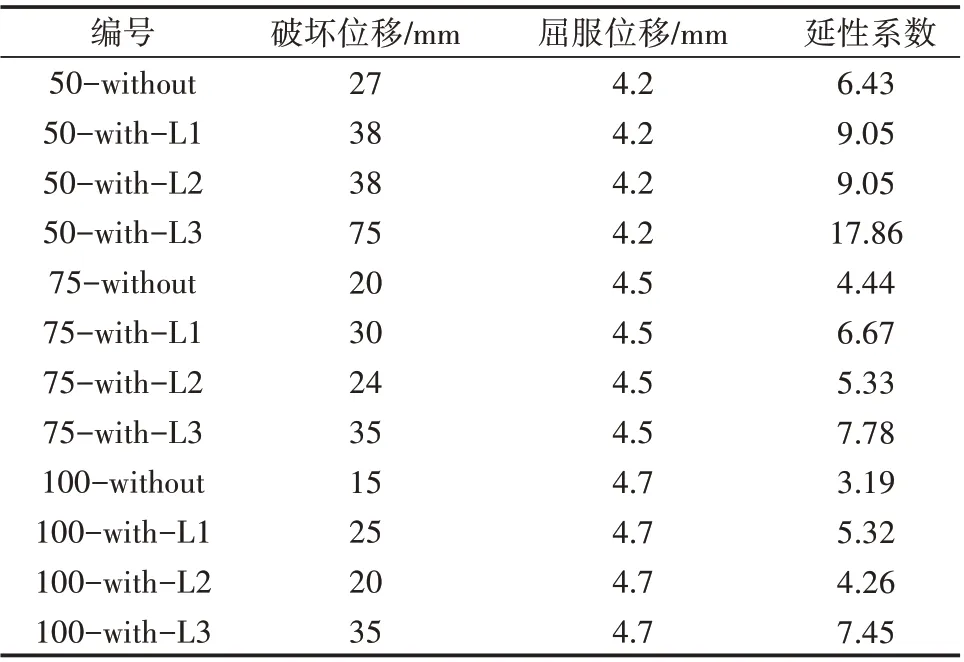
表5 不同工况下结构破坏位移及延性系数
由表5中的不同编号所对应的结构延性系数可知,设置加劲肋可以有效增加结构延性。当径厚比为50时,设置槽型及半圆型加劲肋的结构的延性系数增长幅度均为40.7%,设置三角型加劲肋的结构的延性系数增长幅度为177.6%;当径厚比为75 时,设置3种不同类型的加劲肋的结构的延性系数增长幅度分别为50.5%、20%、75.2%;当径厚比为100时,设置3种不同类型的加劲肋的结构的延性系数增长幅度分别为66.7%、33.5%和133.5%。设置加劲肋提高了结构承载能力,使得结构塑性铰区范围扩大,更多的材料参与受力及耗能;相对于无加劲肋的结构,设置加劲肋的结构在屈曲后塑性阶段变长,对结构延性的提高效果更为显著。就加劲肋横截面类型而言,三角型加劲肋优于槽型加劲肋,槽型加劲肋优于半圆型加劲肋,因此在实际工程中选用加劲肋时应优先选用三角型加劲肋。
4 结 论
本文选取3 种不同径厚比圆钢管,分别研究设置槽型、半圆型及三角型加劲肋对薄壁圆钢管结构抗震性能的影响,通过有限元计算与分析,得到以下结论:
(1)设置加劲肋可以有效防止薄壁圆钢管结构产生局部屈曲,将结构耗能由屈曲铰耗能转变为材料屈服耗能,提高了材料的利用效率。
(2)设置三角型加劲肋,对各径厚比钢管结构的承载能力提高效果比设置槽型及半圆型加劲肋更为明显,对于径厚比为50、75、100的结构,其最大反力分别提高50.0%、42.5%和106.0%。
(3)设置三角型加劲肋对于结构抗延性性能的提升要优于设置槽型和半圆型加劲肋,在实际工程中对于需要设置加劲肋的结构可以优先选择三角型加劲肋,从而降低结构突发破坏的可能性。

