分布位错法求解次表面裂纹的力学行为

李文俊，张雪朋，江晓禹

（西南交通大学力学与航空航天学院，成都 611756）

引 言

随着铁路运输的速度和运载能力的提高，在复杂的工况下，由轮轨滚动导致的钢轨材料的失效越来越严重，而钢轨材料的失效通常是由断裂或者疲劳引起的。材料表面疲劳裂纹的萌生与发展机理非常复杂，引起了国内外专家的广泛关注和深入研究[1-2]。当轮轨与钢轨相接触时，轮轨和钢轨之间的相互作用，将在钢轨内部产生微裂纹，微裂纹一旦产生之后，将会不断的扩展，当裂纹长度达到一定值时，会引起钢轨表面的材料脱落，甚至引起钢轨的断裂，造成严重的列车脱轨事故[3]。

轮轨接触力是一种随时间变化的多轴非比例载荷，在轮轨接触力的作用下，裂纹附近的局部表面上承受较大的压缩应力，会导致裂纹表面闭合和摩擦接触。分布位错法是一种研究裂纹的有效方法，它的主要原理是利用连续分布的位错来等效地代替裂纹。LI 等[4-5]用分布位错法研究了在半无限大的平面内，多个微裂纹对主裂纹的影响，他们的局限在于没有考虑复杂工况，这与实际情况不符。王强胜等[6-7]基于该方法，研究了不同工况下次表面直裂纹的力学性质，但仅考虑了垂直于表面的裂纹，不具有一般性。曹世豪[8]及江晓禹[9-12]等利用有限元，将钢轨简化为半无限大平面，研究了不同轴向载荷和不同裂纹角下，不同裂纹位置的应力强度因子。Tiberiu[13]通过有限元建模，研究了赫兹接触对轮轨接触问题的适用性，发现材料的内部缺陷、内部塑性变形、临界摩擦系数对材料的破坏有直接的影响。以上研究主要是通过有限元模拟不同载荷下裂纹的力学性质，但是对于复杂工况下半无限平面内与自由表面成一定角度的直裂纹，通过理论计算来求解裂纹尖端的应力强度因子解析解，及讨论不同因素对于裂纹扩展的影响方面的研究鲜有报道。为此，本文通过将轮轨载荷等效为赫兹压力，研究在不同的工况下，多种因素对于裂纹扩展的影响，为铁路运输的安全性评估提供参考。

1 理论模型

将轮轨载荷简化为移动的赫兹压力，研究在半无限大平面内一条与自由表面成θ角度的次表面裂纹。如图1 所示，赫兹压力的接触长度为L，从裂纹顶部到表面的距离为a，从裂纹中心到表面的距离为d，从下端到表面的距离为b，与水平面的夹角为θ，为了便于方程的积分，建立了一个局部坐标系，Oi为坐标原点，并且其与中心O的距离为y=iL，赫兹压力以长度L间隔从左往右进行移动。假设半无限大的弹性平面只受到赫兹压力的作用，由于裂纹面在轮轨载荷的反复研磨下，比较光滑，为了简化计算，忽略裂纹面接触摩擦力的作用。根据文献[14-15]中提出的方法，可获得滑移面上产生的应力。

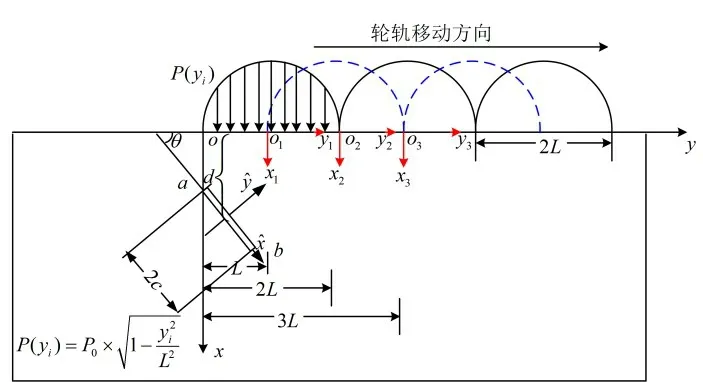
图1 赫兹压力作用下次表面裂纹问题模型

2 理论求解

2.1 叠加原理

图1中，为了得到裂纹面上的应力场，可以利用Bueckner原理将移动赫兹压力下的半无限平面内的次表面裂纹问题分解为两个子问题。为了满足叠加原理使用条件，即裂纹面为自由表面，两个子问题分别为，子问题1：求解在无裂纹的半无限平面上由赫兹压力产生的应力；子问题2：求解与子问题1大小相等方向相反的方向载荷。由弹性力学Flamant 解[16]求解子问题1，而子问题2 可以通过分布位错方法进行求解，再叠加这两个子问题，可以获得问题的最终解决方案，即获得裂纹面上的应力：

其中：N(x)为法向应力，S(x)为切向应力。

2.2 赫兹压力泰勒展开

由于赫兹压力无法直接在裂纹面上积分，为了简化运算又不失精度，对赫兹压力进行泰勒展开到一定的阶次，运用Gauss—Chebyshev 数值求积方法求解，由于在赫兹压力作用下，裂纹面在压应力作用下处于闭合状态，裂纹主要是发生滑移破坏，因此通过上述方法计算裂纹尖端KII的数值解。

从弹性力学的Flammant 解出发，Taylor 展开后可以直接积分赫兹压力，从而得出平面内裂纹上的应力表达式。分布位错会导致接触面的变形，为了简化运算，将界面压力与赫兹压力等效：

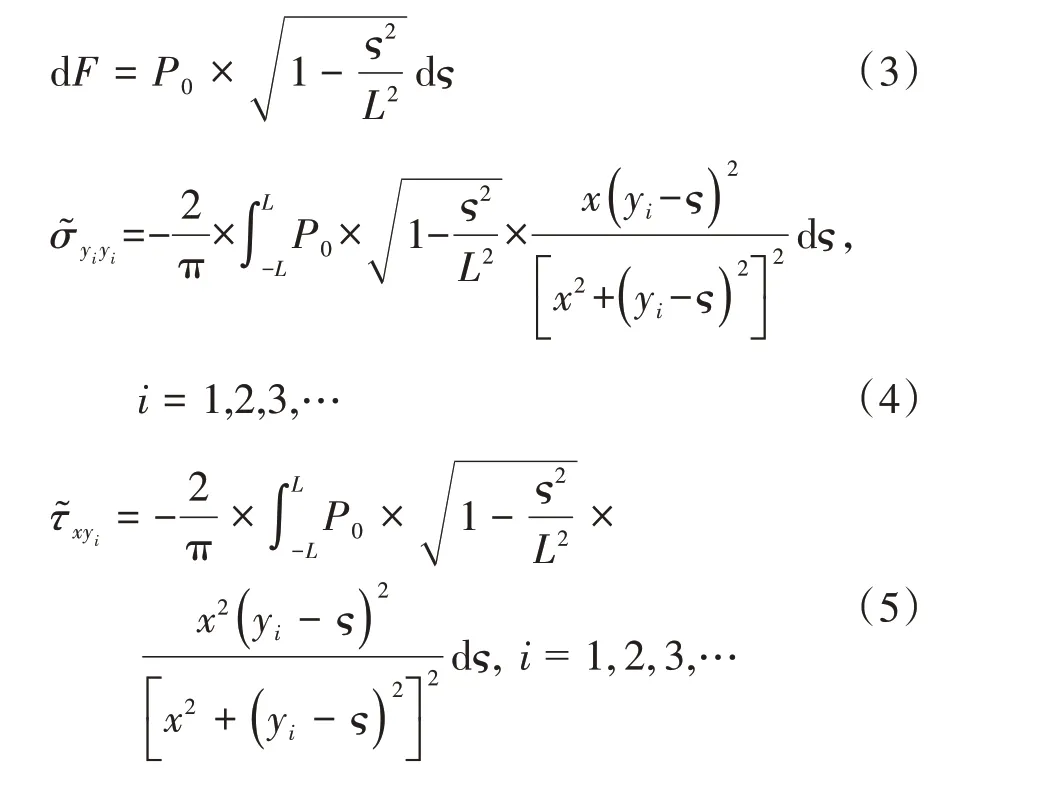
将式（7）代入式（4）～（6）中，则：

图2 所示为赫兹压力展开为不同阶次时，应力随无量纲化距离x L的变化情况。图2 中，2-σyy、2-τxy、2-σxx分别表示式（7）展开为两项时对应的压应力、切应力和水平应力。由图2可见，幂级数在展开到6 项之后，应力值变化非常小，为了计算方便，又不丧失精度，将式（7）展开为6项代入后文进行数值计算。图3所示为赫兹压力位于平面上不同位置时，裂纹面上应力值的变化情况。由图3可见，裂纹面上应力值随着赫兹压力的移动而变小，当x/L= 4时，应力值的变化趋于平缓。

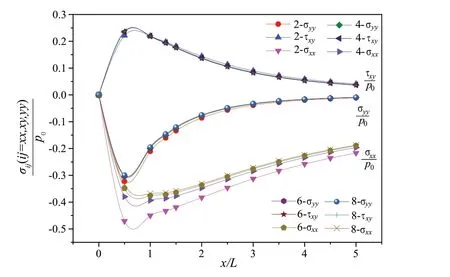
图2 当赫兹压力泰勒扩展到不同阶时的应力变化

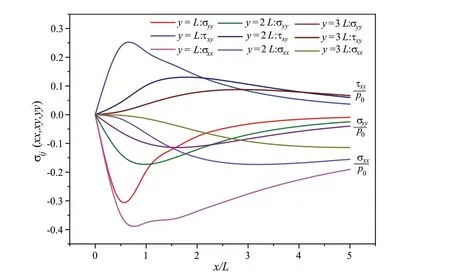
图3 赫兹压力在不同位置时的应力值

2.3 位错密度积分方程的建立

裂纹线(ς,0)处存在位错，Burgers的分量分别为bx和by，则位错产生的应力[17]通过下式计算：

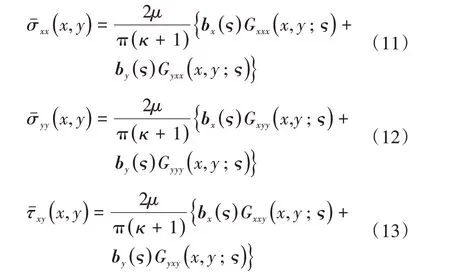
其中：μ为剪切模量，κ为Kolosov常数。

图3 中可见，σyy/p0< 0，因此，图1 中的裂纹表面始终承受压缩载荷而保持闭合，并且裂纹可以等效于滑动错位，影响函数Gijk描述裂纹面上一点位错对于裂纹面上的任意一处位错的影响，影响函数Gijk可由文献[17]得出，裂纹面(ŷ= 0)上,法向和切向应力为：

可以通过转换矩阵A[17]来实现局部坐标与全局坐标的影响函数的转换：

上式中：等号左边为局部坐标系下的影响函数，等号右边则为全局坐标系下的影响函数。

2.4 数值求解位错密度积分方程

由于位错密度积分方程式(16)～(17)很难求解解析解，因此使用Gauss-Chebyshev 积分方法，将积分区间(a,b)用式（19）规范化，得到归一化区间(-1,1)：

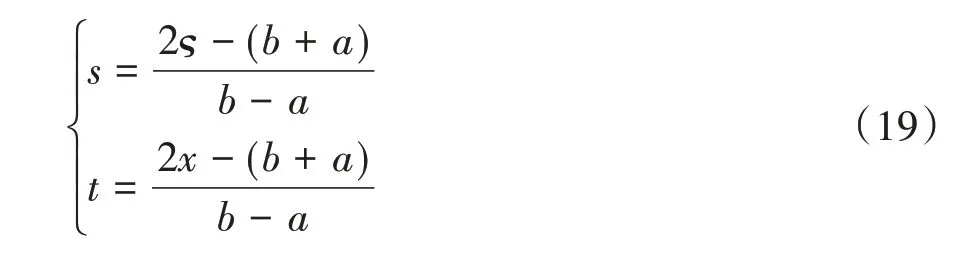
通过Gauss-Chebyshev 数值求积方法，将式(16)～(17)的两个方程各离散为(N- 1)个方程：

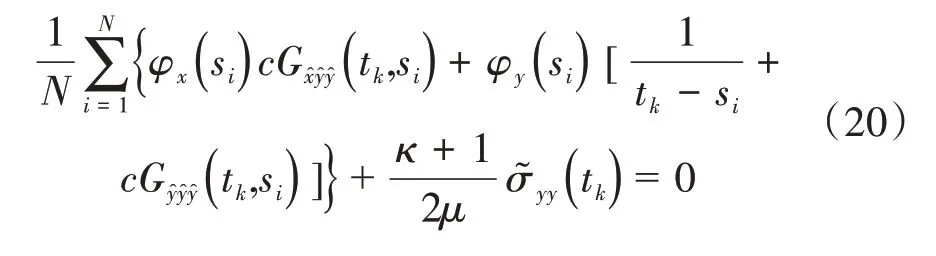
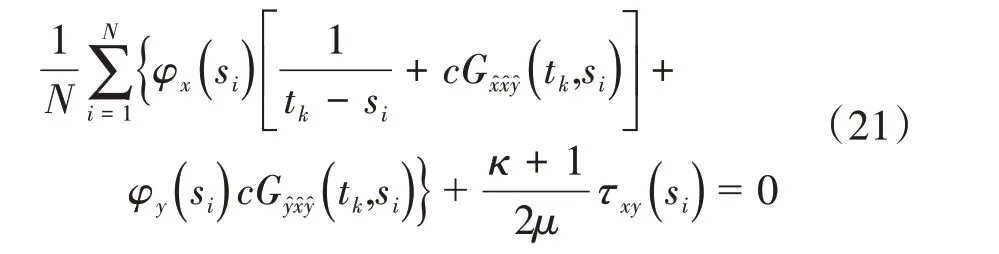
其中：c为裂纹的一半长度。需要两个附加方程来求解未知函数ϕ(s)，由于从裂纹表面的一端到另一端没有净位错，因此可以得到两个附加方程为：

式(22)可以离散为：

在式（20）～（23）中设置N个离散积分点si和(N- 1)个相应的配置点tk，离散积分点和配置点可以从文献[17]中得到：

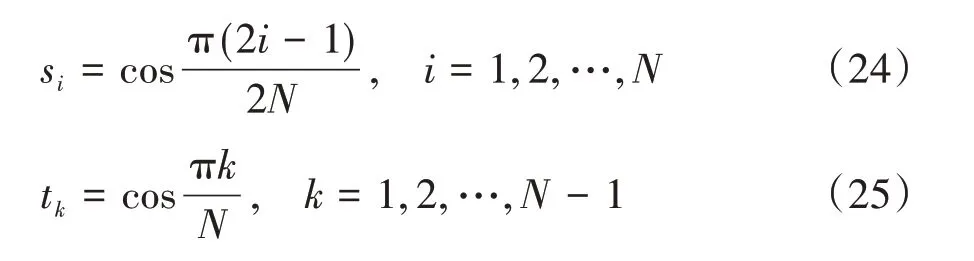
由式（20）～（23）解出ϕ(si)，可由式(22)得到位错密度函数：

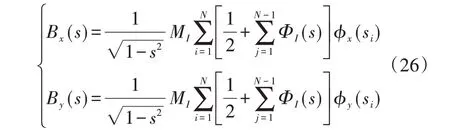
由式（23）与Krenk 插值公式，可以得到裂纹两端应力强度因子为：

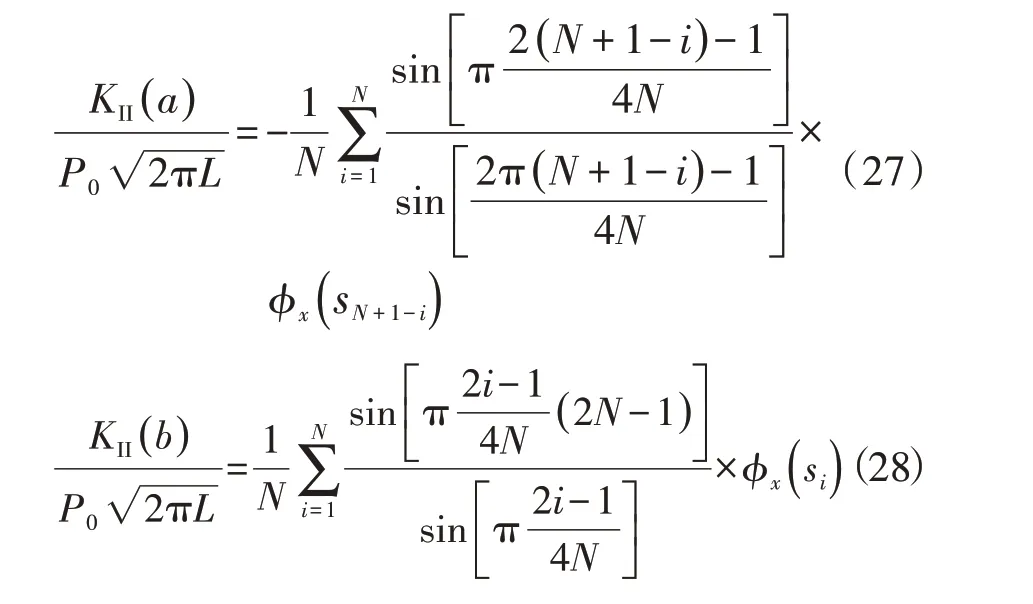
3 结果验证

为保证数值积分方法的正确性，将图1 中裂纹设置为与自由表面平行。在文献[18]中将轮轨载荷等效为赫兹压力，研究在赫兹压力作用下次表面水平裂纹的扩展规律。本文与文献[18]中裂纹尖端二型应力强度因子的对比如图4 所示，图中d为裂纹与自由表面之间的距离。图4 可见，随着赫兹压力的移动，裂纹位于接触斑中心时最大，且该方法与文献[18]的计算结果是基本吻合的，因此本文采用的方法所得到的最终结果是可靠的。

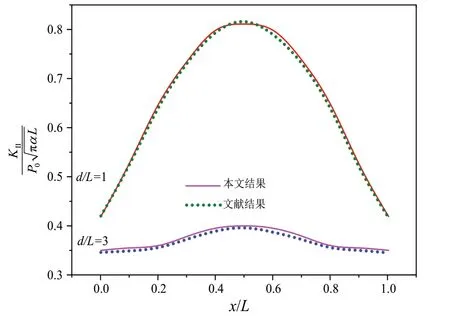
图4 与文献[18]结果的对比

4 结论与分析

4.1 赫兹压力在不同位置时对于KII的影响

裂纹的深度和长度均取为定值（d= 0.6，c=0.5）时，计算了赫兹压力在移动过程中裂纹尖端应力强度因子的变化情况，如图5 所示。由图5 可以看出，裂纹尖端应力强度因子在赫兹压力处于自由表面（0，L）处时，应力强度因子呈先减小后增大的趋势。当裂纹沿水平方向时，裂纹两端处应力集中程度比较强，裂纹容易沿水平方向扩展，导致钢轨表面的剥离。随着赫兹压力远离裂纹，当赫兹压力处于自由表面（0，2L）处时，裂纹尖端的应力强度因子整体呈减小的趋势，但裂纹两端的应力强度因子随着与自由表面夹角的改变呈现出不同的变化规律，b端是先减小后增大，而a端是先增大再减小。在轮轨载荷的反复作用下，这些现象对于裂纹扩展有非常大的影响，下文将会对这些因素进行进一步的探讨。

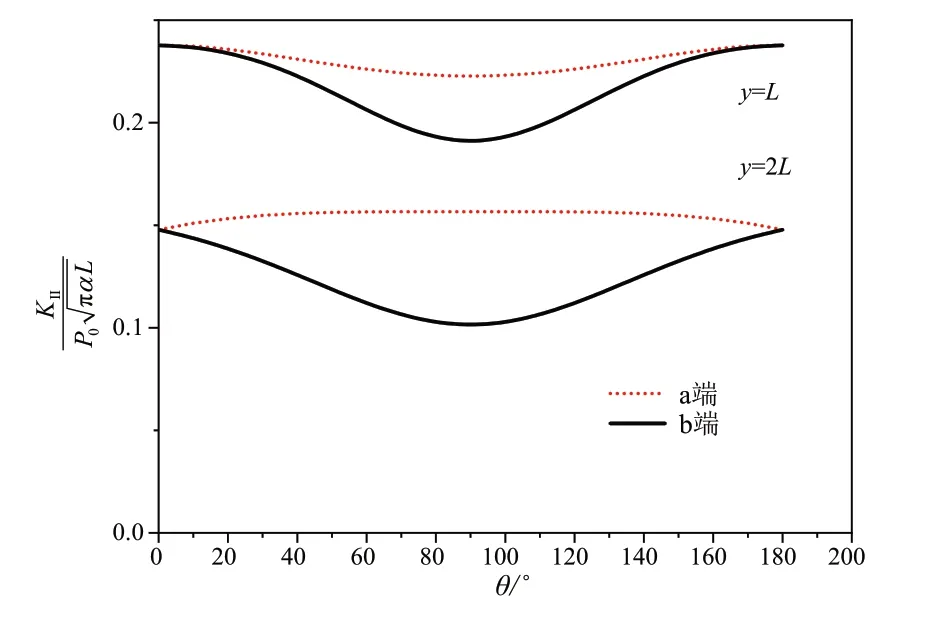
图5 赫兹压力位于在位置对于KII的影响

4.2 裂纹深度对于KII的影响

当裂纹长度取为定值(2c/L= 1 )时，裂纹尖端应力强度因子随着裂纹深度改变的变化趋势如图6所示。在次表面裂纹非常靠近自由表面的情况下，当裂纹与自由表面平行时，裂纹尖端处应力集中程度较大，裂纹容易从两端处发生扩展，造成表面的剥离。随着裂纹深度的增加，裂纹尖端的应力强度因子整体呈减小的趋势，说明裂纹的深度对于裂纹尖端的应力强度因子影响较大。与裂纹非常靠近自由表面不同的是，此时裂纹尖端处的应力强度因子出现了截然不同的变化趋势：裂纹较浅时，裂纹a端容易扩展；而随着裂纹深度的增加，a端变得不容易扩展，b端更容易扩展。即：裂纹离自由表面更近时，裂纹容易往自由表面扩展；当裂纹深度达到一定值时，裂纹容易往钢轨内部扩展。当裂纹与自由表面垂直时，裂纹总是容易朝着一端扩展且与裂纹的深度无关，裂纹容易扩展的方向跟裂纹与自由表面的夹角有关。

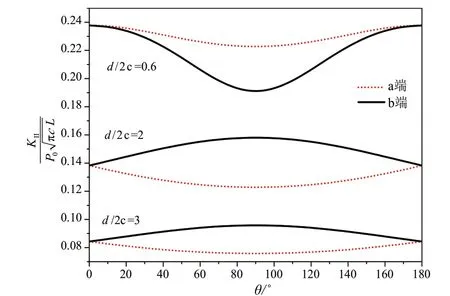
图6 裂纹深度对于KII的影响

4.3 裂纹长度对于KII的影响

当裂纹的深度(d/L=2 )为定值时，裂纹长度的改变对于裂纹尖端应力强度因子的影响如图7 所示。当裂纹沿着水平方向，赫兹压力在裂纹两端产生的应力强度因子保持不变，裂纹尖端应力强度因子只与裂纹的深度有关，裂纹的长度不会对裂纹尖端应力强度因子产生影响，裂纹长度的改变不会引起裂纹尖端的应力集中程度的变化。当裂纹与自由表面趋近于垂直时，此时裂纹两端的应力强度因子变化趋势相反，裂纹的一端应力集中比另外一端更加明显，裂纹更容易向一端扩展。裂纹长度的增加会加剧裂纹一端的应力集中程度，即裂纹越长越容易扩展。

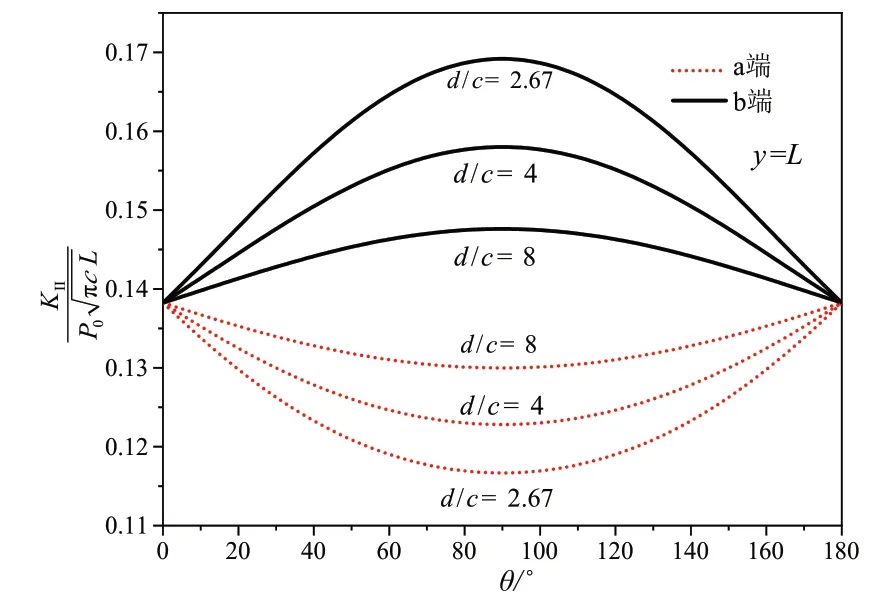
图7 裂纹长度对于KII的影响

5 结论

通过将轮轨载荷等效为赫兹压力，研究在不同的工况下，赫兹压力位置、裂纹长度、裂纹深度和裂纹与自由表面夹角之间的相互作用对于裂纹扩展的影响，得出结论如下：

（1）将裂纹等效为均匀分布的位错，通过对裂纹的理论求解，可以改变载荷的施加方式，得到更为复杂的条件下，裂纹扩展与自由表面夹角之间的关系。

（2）随着赫兹压力的移动，在裂纹深度和长度取一定值时，赫兹压力离裂纹越远，裂纹尖端的应力集中程度越小，裂纹越不容易扩展。

（3）在次表面裂纹非常靠近自由表面的情况下，且裂纹与自由表面平行时，裂纹容易从两端处发生扩展，造成表面的剥离。裂纹离自由表面更近时，裂纹容易往自由表面扩展，当深度达到一定值时，裂纹容易往钢轨内部扩展，裂纹长度的增加会加剧裂纹一端的应力集中程度。