基于梯形模糊互反判断的一致性分析

刘万里,刘卫锋,何 霞

(郑州航空工业管理学院 数学学院,河南 郑州 450046)

1 引 言

由Saaty[1]建立的层次分析法(简称AHP)是一种多目标决策方法,在许多领域得到了广泛的应用。随着研究的深入，经典的层次分析法(AHP)已经扩展到模糊判断形式(包括区间数判断、三角模糊判断和梯形模糊判断)，这更适合于表达人类的直觉。 众所周知，使用AHP进行决策时，判断的一致性问题是衡量决策合理性和准确性的关键问题，因此关于判断的一致性研究一直是模糊层次分析法中的重要课题。关于区间判断的一致性研究[2-7]和三角模糊判断的一致性的讨论[8-18]已经获得很多成果，研究内容比较丰富，但没有一个统一的标准。其中Buckley[14]是利用模糊传递公式来定义三角模糊互反判断的一致性问题，而Dubois[15]认为这种一致性事实上是不存在的。Wang等[16]针对三角模糊互反判断的一致性概念提出若干性质用以完善模糊FAHP。Meng等[17]利用割集方法把三角模糊互反判断转化为区间数互反判断，然后利用区间数互反判断的一致性来定义三角模糊互反判断的一致性问题。Liu等[18]利用分解方法把三角模糊数的元素分解为三个数字互反判断矩阵，按经典的Saaty的一致性指标来检验。而关于梯形模糊互反判断的一致性研究相对较少，现有的研究也都存在不少问题，需要补充完善。针对梯形模糊互反判断，Buckley[14]最先给出一种一致性定义，所给出的判断方法仅仅用梯形模糊数的中间两个元素所构成的区间数的信息来处理，此方法理论根据不够充分，实际操作不便进行，因此该方法不被广泛接受。Meng等[17]比较严密地给出了梯形模糊互反判断的一致性定义，但是缺乏判定方法，无法用有限计算进行一致性检验。Wang[2]虽然巧妙地解决了区间判断的一致性检验问题，但对于梯形模糊互反判断的一致性问题是利用割集方法转化为区间数来处理，此方法需要进一步完善。

Liu等[18]通过对梯形模糊判断矩阵进行分解，把每个梯形模糊数的4个元素分开，分别建立4个数字互反判断矩阵，然后针对每个数字互反判断矩阵，使用经典的AHP检验一致性指标进行检验。Zhang等[19]通过举例说明文献[18]所提出的关于梯形模糊互反判断一致性定义的不足和不稳定性，并给出一种满意一致性的定义方法。

Zhang等[19]所给出的检验一致性方法是通过梯形模糊数的元素利用几何平均的方法建立两个经典的数字互反矩阵，用这两个经典的数字互反判断矩阵的一致性指标作为依据，从而检验一致性是否满意。但该方法忽视了梯形模糊数分散性的作用，且没有提供充分的理论根据。吕智颖等[20]针对梯形模糊互反判断矩阵提出一种满意一致性定义方法，该方法是通过建立排序判断矩阵，然后根据排序判断矩阵是否出现循环现象来判断一致性是否满意。该方法思路很好，但是使用范围有一定的局限性。本文针对梯形模糊互反判断矩阵将提出一种新的一致性定义和检验方法。本方法基于相容性的概念，根据一致性的传递思想，把满足逻辑顺序作为检验的条件，给出检验定理。本方法统一了梯形模糊判断、三角模糊判断和区间数判断三种形式，并且避免了固定阈值指标的限制，简单实用。

2 知识回顾

为了表示不确定性，实数被扩展到区间数、三角模糊数以及梯形模糊数。

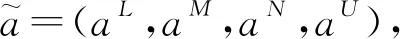
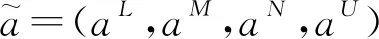
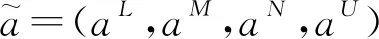
定义2[20]设S1,S2,…,Sn是n个方案,由两两重要性比较所产生的判断矩阵如(1)所示：

(1)

注1 主对角线上元素 “1” 可以写为(1,1,1,1),即1=(1,1,1,1)。

3 有关梯形模糊互反判断的一致性概念

定义4对构成梯形模糊数的元素使用几何平均算法给出了一种检验TFRJM一致性的简单方法。但是由于平均数只体现了集中程度，而梯形模糊数的分散程度未能体现，这种检验可能会把本该不满意一致性判断成满意的。

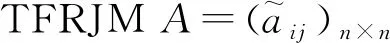
总之，目前大多数方法都有两个共同的特点，一是把TFRJM 转化为若干个数字互反判断矩阵，然后使用Saaty的方法进行检验；二是用有限的判断来决定无限状态的一致性。这是目前的研究难以回避的痛点，因为这两点的理论根据不充分也不严谨。为了克服以上两个痛点，下面给出一种新的定义方法。

4 梯形模糊互反判断矩阵的一致性新概念

本文的理论根据是：不管怎样判定，在一致性传递下，组成梯形模糊数元素的逻辑大小顺序不容改变。即对于任意的i,j,k=1,2,…,n,应当满足

(2)

否则令人难以接受。

为此，下面首先给出相容性定义，然后基于相容性将给出一种新的满意一致性定义和判定定理。

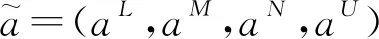
比如两个梯形模糊数(1,3,5,7)与(2,4,6,8)是相容的，因为[1,3]∩[2,4]=[2,3]≠φ和[3,5]∩[4,6]=[4,5]≠φ及[5,7]∩[6,8]=[6,7]≠φ。而(1,2,3,4)与(4,5,6,7)是不相容的，因为[1,2]∩[4,5]=φ。

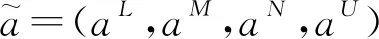
注4 定义7包括两层含义：

所以，由定义7可得出如下定理：

(3)

(4)

(5)

根据定义7该定理结论显然成立，在此略证。

由定理1中(3)—(5)可以看出定义7隐含着梯形模糊判断中保持着元素的逻辑顺序，虽然没有明确的数值指标，但给出了明确的定性的顺序约束条件。一般情况下，一个梯形模糊互反判断起码满足定理1的三个条件才能令人接受，因此该定理可以作为检验满意一致性的判定定理。

证明：必要性是显然的。

此表明，当A的上三角元素满足满意的一致性判定定理的条件时，下三角元素也同样满足。

由定理2可知，在检验满意一致性时，只需要验证矩阵A中的上三角元素即可。

注5 当检验TFRJM不具有满意的一致性时，只要找到一个不满足(3)或(4)或(5)的元素即可。关于三角模糊互反判断矩阵以及区间数互反判断矩阵的一致性定义和判定定理可类似给出。

下面仅给出三角模糊互反判断矩阵的满意一致性的定义、判定定理,关于区间数互反判断矩阵的满意一致性的定义、判定定理可参看文献[2]。

(6)

注6 以上理论方法同样适合于区间数互反判断矩阵的一致性问题[2]，所以本研究把三种互反判断矩阵的一致性问题统一起来。

5 示 例

例1设有2个梯形模糊互反判断矩阵如下：

根据定理2， 经过计算A1中所有上三角元素都满足不等式(3)—(5)，所以矩阵A1具有满意的一致性；而对于A2经计算可知：

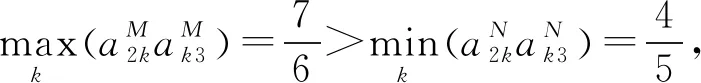
为了进一步比较，同时也为了给出此法对三角模糊互反判断的应用，参看下例。

例2 下面2个三角模糊互反判断矩阵

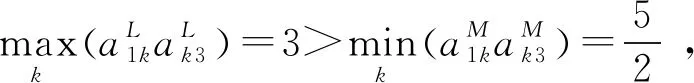
结果比较分析：

本文的理论根据就是一致性的传递结果具有相容性，即至少满足条件(2)，如果不满足条件(2)而被接受可认为该判定方法是不合适的。就目前来看，文献[19]的方法是简单可行的，下面把本方法同文献[19]中的方法进行比较。

例1中A1和A2是两个梯形模糊互反判断矩阵，例2中A3和A4是两个三角模糊互反判断矩阵。使用文献[19]中的方法检验结果显示A1、A2、A3和A4都具有满意的一致性。而使用本方法检验结果显示A1和A3具有满意的一致性，A2和A4不具有满意的一致性，即A2和A4不满足本方法的必要条件(2)。这说明在对A1和A3检验时,本方法与文献[19]中的方法具有相同的效力，而在对A2和A4检验时，结果是不同的，也就是说使用文献[19]中的方法，存在不满足逻辑顺序(2)的条件下可以接受的情况。究其原因，我们发现文献[19]中的方法仅使用几何平均法却忽视了模糊数的分散性，所以在检验时一致性容易满足。因此可以认为文献[19]中的方法分辨力较弱，而本方法可认为是一种改进。

6 结束语

本文对梯形模糊互反判断矩阵的一致性进行了详细讨论，并针对梯形模糊互反判断提出了满意一致性的定义和判定定理。该方法把梯形模糊互反判断矩阵、三角模糊互反判断矩阵和区间数互反判断矩阵统一起来，给出了一种形式相似的满意一致性定义和判定定理，克服了以往借用Saaty方法的约束和有限判断的不严谨性，既简单又实用。最后通过例子显示了该方法的可行性和有效性。本文仅仅考虑了一致性问题，关于方案权重计算的研究将是我们下一步的研究课题。