钢支撑伺服系统地铁深基坑微变形控制技术研究

任一恒，李恒一，何晟亚

（广州地铁设计研究院股份有限公司，广东广州 510010）

1 前言

地铁车站基坑支护方式主要有地连墙与支撑、支护桩与支撑、吊脚桩、吊脚墙等；其中，周边环境位移控制严格情况下所适用的基坑支护方式，主要是地连墙与支撑的方式。由于现在较多地铁车站基坑邻近高速公路、高速铁路、城际铁路等位移控制严格的建（构）筑物，该方面的研究也日渐成熟，但采用上述传统方式支护仍无法满足部分情况下的严格位移要求。

在基坑支护结构发展过程中，越来越多的学者开始研究不同的基坑支护问题。陈璟斌[1]研究不同深基坑开挖过程对邻近桩基的影响；吴士德[2]研究地铁车站基坑开挖对邻近桩基础的影响；万鹏[3]研究软土中基坑开挖对既有高架桩基础的影响；郑灿政[4]研究基坑降水对高铁桩基础的影响；黄艳珍[5]研究基坑降水及孔隙比随深度变化对基坑周边桩基础的影响；李睿峰[6]研究复合地层基坑开挖对周边既有建（构）筑物的影响。国外学者亦有相关研究，Finno[7]研究基坑开挖对群桩的影响；Poulos[8]研究无支护开挖情况下，基坑侧向土体位移对桩基础的影响；Leung[9]研究基坑开挖对桩基础变形的影响；Ong[10]研究采用地连墙支护过程中，基坑开挖对周边土体的影响等。但以上相关研究很少涉及钢支撑伺服系统。

钢支撑伺服系统是在现代基坑支护方式的发展过程中衍生出的新型支护形式；支撑受力方式由原来被动受力，调整为主动受力；由此更好地控制周边土体的位移，并有效地控制基坑开挖过程中周边重要建（构）筑物的变形。本文对钢支撑伺服系统的研究主要从钢支撑的建模模拟方式、采用伺服系统的各工况位移值计算等方面进行。

2 模型建立与条件假设

2.1 数值模拟软件选取

Midas/GTS NX软件是用于土木工程等领域的有限元分析软件；它基于最新分析理论设计而成，具有施工阶段的应力分析和渗透分析等岩土和隧道所需的几乎所有分析功能，是岩土和隧道分析与设计的解决方案之一。

岩土分析一般对材料进行非线性分析。材料的非线性特性可从岩土的初始条件，即施工前的原场地条件获得。后续信息通过按施工顺序进行施工全过程分阶段分析得到。现场的实际施工条件非常复杂且经常变化；通常将其简化，取比较重要的阶段进行分析。

Midas / GTS NX的施工阶段分析采用的是累加模型，即每个施工阶段都在继承上一个施工阶段分析结果的基础上继续累加本施工阶段的分析结果，也就是说上一个施工阶段中结构体系与荷载的变化会影响到后续阶段的分析结果。本研究利用Midas / GTS NX建立的基坑支护计算模型研究钢支撑伺服系统。

2.2 模型建立

本文依托工程为深圳地铁12号线和平站基坑工程，具体站位情况如图1所示。在实际工程中，由于变形控制要求及工程成本考虑，仅对穗莞深城际铁路高架下穿段（9～16轴）采用伺服钢支撑（布置于第二～五道，第二道23根、第三道26根、第四道23根、第五道23根；共95根），故本文仅以和平站基坑下穿段作为研究对象，通过数值模拟来验证双控法思路指导下的基坑支护效果。

按照工程实况建立和平站基坑下穿段三维模型。地层主要为淤泥和黏土。为避免边界效应对计算结果的影响，模型大小为90 m×120 m×100 m （X×Y×Z），基坑开挖深度为16.8 m，开挖宽度为21 m，两侧分布有穗莞深城际铁路高架30号、31 号桥墩；其中，31号桥墩距基坑边缘约22.5 m，30号桥墩距边缘约7.5 m，两桥墩的承台尺寸为10.5 m×18.5 m×3 m，加台尺寸为5 m×15.6 m×1 m。桥墩与基坑之间的土体采用隔离桩和旋喷桩进行加固，如图 2所示；旋喷桩作用效果可通过将区域土体的弹性模量提升为原来的2倍来等效模拟。整个模型共有18142个节点，33871个单元，如图3所示。

2.3 条件假设

本文为简化模型及减少计算量，对模型的建立及分析提出以下假定。

（1）模型初始地应力平衡只考虑自重应力，忽略构造应力的影响。

（2）依据拟建基坑与穗莞深城际铁路30号及31号桥墩空间位置关系，近似认为基坑走向与桥梁轴线正交。

（3）依据地质勘测资料，近似认为地面为平面，忽略地形起伏的影响。

（4）基坑施工时井点降水已施工完毕，地下水位位于主体结构底板以下，因此不考虑基坑施工过程中降水固结的影响。

（5）根据设计资料，隔离桩直径800 mm，间距1000 mm，通过旋喷桩进行咬合；故为方便建模，将隔离桩按刚度等效原则，等效为与之受力形式相近、具有一定厚度的地下连续墙，计算公式为：

式（1）中，D0为等效地下连续墙厚度；L为桩间距；D为桩径。故隔离桩等效地下连续墙的厚度为0.623 m。

依据《公路与市政工程下穿高速铁路技术规程》[11]（TB 10182-2017）要求，受下穿工程影响的高速铁路桥梁墩台顶位移限值为2 mm，由相似三角形推导出桩基位移限值为5 mm。

3 钢支撑伺服系统研究

3.1 钢支撑模拟方式

伺服钢支撑采用双控法确定设定轴力，传统钢支撑采用弹性基点法确定预加轴力，具体取值见表1。需要注意的是，由于本部分研究的工况较多，故不再采用双控法对各工况逐一调试；各道伺服钢支撑的设定轴力应取调整历程中的最大值。实践工程经验及总结表明，各根支撑的受力之间存在相互关系，某根支撑的卸荷会带来临近支撑受力的增加。因此，在穗莞深下穿段的伺服系统实际使用过程中，只要支撑轴力不超过钢支撑安全上限，原则上不予卸载。在基坑开挖推进过程中，将已施加的伺服钢支撑轴力严格控制在设定轴力值上，以等效模拟伺服系统对支撑轴力的补偿性能；传统钢支撑仅在初设时通过施加预加轴力进行一次干预，后续施工过程中的轴力由软件根据土体及支护受力平衡自行计算得出。

表1 2类钢支撑轴力表 kN

3.2 各工况伺服系统计算研究

依据如表2所示的工况，分别分析采用伺服系统钢支撑的地铁基坑在开挖过程中的基坑变形及穗莞深桩基础变形情况。

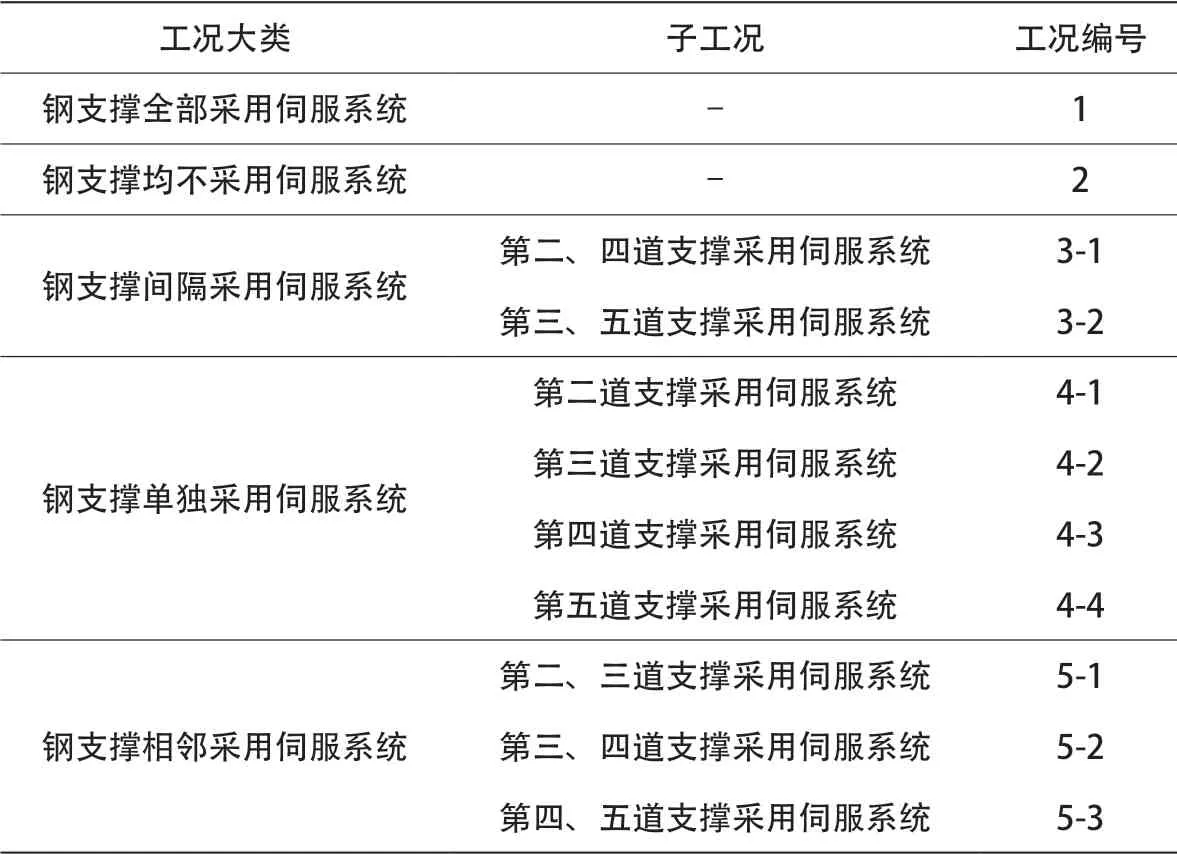
表2 伺服钢支撑布置方式研究工况

全部采用钢支撑伺服系统的情况下，相关计算结果如图4所示。

当全部采用伺服钢支撑时，南、北两侧地下连续墙的最大侧向位移值分别为4.8 mm和4.0 mm，均满足规范要求[11]中的微变形控制要求（5 mm）；整体而言，基坑南侧（31号桥墩侧）的地下连续墙变形量大于基坑北侧（30号桥墩侧）。当进行开挖-5和开挖-6时，标高在-23.0～-17.0 m范围内的地下连续墙侧向位移发生较明显的增长，需要给第四、五道伺服钢支撑提供较大的设定轴力才能保证其满足微变形控制要求。

全部不采用钢支撑伺服系统的情况下，相关计算结果如图5所示。

当不采用伺服系统时，基坑南、北两侧地下连续墙的侧向位移均呈明显增长趋势；最大位移值分别为 6.2 mm 和5.4 mm，不满足规范[11]中的微变形控制要求。对于标高-15.0 ～0.0 m范围内的地下连续墙，其侧向位移值要比全部采用伺服系统时明显减小。但该标高范围内的伺服钢支撑设定轴力与传统钢支撑预加轴力的取值相近；这说明，伺服系统可对钢支撑轴力进行补偿，保证支撑体系能够对地下连续墙起到较稳定的支撑作用；而传统钢支撑的轴力难以进行灵活调控，只能在初设支撑时通过施加预加轴力的方式进行一次性加载，无法对施工过程中多方面因素导致的轴力损失及时有效地进行补偿，难以实现理想支撑效果。

间隔采用钢支撑伺服系统的情况下，对第二、四道钢支撑采用伺服系统时，南、北两侧地下连续墙的最大侧向位移值分别为5.6 mm和4.8 mm，南侧地下连续墙不满足规范[11]中微变形控制要求（5 mm）；对第三、五道钢支撑采用伺服系统时，南、北两侧地下连续墙的最大侧向位移值分别为5.4 mm和4.6 mm，不满足规范中[11]微变形控制要求。从变形控制效果来看，对第三、五道支撑采用伺服系统要优于对第二、四道支撑采用伺服系统。这是因为地下连续墙结构的深部侧向位移要大于浅部，当伺服钢支撑的整体布置标高偏低时，可对地下连续墙的最大位移起到有效抑制作用。

单独采用钢支撑伺服系统的情况下，当对第二道、三道、四道、五道钢支撑采用伺服系统时，南侧地下连续墙的最大侧向位移值依次为5.9 mm、5.9 mm、5.6 mm、5.4 mm，北侧地下连续墙的最大侧向位移值依次为5.1 mm、5.1 mm 、 4.8 mm、4.6 mm 。

相邻采用钢支撑伺服系统的情况下， 当对第二、三道，三、四道，四、五道钢支撑采用伺服系统时，南侧地下连续墙的最大侧向位移值依次为5.6 mm、5.5 mm、5.1 mm，北侧地下连续墙的最大侧向位移值依次为 4.8 mm、4.7 mm、4.2 mm。其中，南侧地下连续墙均不满足规范[11]微变形控制要求，北侧地下连续墙均满足规范[11]微变形控制要求。对第四、五道钢支撑采用伺服系统时（计算结果如图6所示），南侧地下连续墙最大侧向位移值为5.1 mm，与控制要求较为接近；这也是所有研究工况中，除全部采用伺服系统外的最优布置方式。

4 结论

通过数值模拟分别计算各工况下，穗莞深城际高架桩基础位移，得到以下结论。

除工况1满足规范[11]微变形控制要求（5 mm），其余工况均不满足微变形控制要求（5 mm）。这说明对于穗莞深下穿段基坑，有必要采用伺服系统对两侧地下连续墙变形进行严格控制，且在不改变其他变形控制措施的前提下，全部采用伺服系统是唯一保证两侧均满足微变形控制要求的布置方式。另外，不采用伺服系统时地下连续墙位移值最大的情况侧面反映伺服系统可有效改善地下连续墙变形控制效果。

当对两道钢支撑采用伺服系统（间隔、相邻布置）时，对二、四，二、三道采用伺服系统时的南侧（北侧）地下连续墙位移值为5.6 mm（4.8 mm），三、四道采用时位移值为5.5 mm（4.7 mm），三、五道采用时位移值为5.4 mm（ 4.6 mm），四、五道采用时位移值为5.1 mm（4.2 mm）；当对第二～五道钢支撑单独采用伺服系统时，南侧（北侧）地下连续墙最大位移值依次为5.9 mm、5.9 mm、5.6 mm、5.4 mm （5.1 mm、5.1 mm、4.8 mm、4.6 mm）。

地下连续墙最大侧向位移与伺服系统平均标高关系如图 7所示。由该图可得出以下结论。

（1）当间隔或相邻布置伺服系统时，地下连续墙的变形控制效果由两道伺服系统的平均标高来决定；总体来看，平均标高越低，变形控制效果越好，且随着平均标高降低，最大位移值衰减速率增大，当平均标高由-10.5 m降至-12.0 m时，变形控制效果明显提升。

（2）对于单独布置伺服系统的情况，当支撑架设标高由-4.5 m降至-7.5 m时，最大侧向位移值无明显变化；随着标高进一步降低，位移值衰减速度增大，但在平均标高为-10.5～-13.5 m时，位移衰减速度小于采用双伺服系统的情况。

（3）随着伺服系统的平均标高降低，地下连续墙侧向位移控制效果得到明显改善。这说明对于穗莞深下穿段基坑，对地下连续墙深层位置侧向变形的控制是关键；而在浅层位置布设伺服系统的控制效果欠佳，可通过适当调低第四、五道钢支撑的架设位置来进一步优化控制效果。另外，当对第四、五道钢支撑采用伺服系统（平均标高-12.0 m）时，南、北两侧位移值分别为 5.1 mm和 4.2 mm，已十分接近位移控制标准。鉴于钢支撑伺服系统的价格昂贵，可尝试对第一、二道钢支撑酌情不采用伺服系统，并进一步加强其他变形控制措施，以实现在变形量满足要求的基础上尽可能降低工程成本的目的。

当仅对第五道钢支撑采用伺服系统时，南、北侧地下连续墙最大侧向位移值分别为5.4 mm和4.6 mm；其变形控制效果优于对第二和四道、第二和三道、第三和四道钢支撑采用伺服系统的情况。这说明，伺服系统数量并不是越多越好，若布置方案设置不合理，也难以发挥伺服系统的变形控制效果。