可解释性预测分析方法的研究
李庆国,康 蕴,余 斌
(1.湖南大学 数学学院,湖南 长沙 410082; 2.湖南师范大学 信息科学与工程学院,湖南 长沙 410006)
粗糙集(rough set)理论[1-2]是一种理想的处理复杂不确定问题的数学工具。在知识表示上,它通过数据集合的近似来描述对象之间的不确定关系;在知识发现上,它在保持分类能力不变的前提下,通过属性约简导出概念的分类或决策规则。它被广泛应用于模式识别、不确定性分析、数据挖掘、知识发现和决策等领域。粗糙集模型也是一种典型的粒计算理论模型[3],经典的Pawlak粗糙集理论是利用等价类来描述“粒度”,用等价关系所诱导的划分来描述粒度空间。从二元关系来看,基于等价关系的Pawlak粗糙集模型太过严格;从粒度空间来看,Pawlak粗糙集模型刻画的粒度空间太过宽松,所以经典的Pawlak粗糙集远不能满足实际应用的需求。因此,学者们基于这两个方面进行改进,提出了一些极具代表意义的拓展的粗糙集模型:模糊粗糙集、粗糙模糊集、概率粗糙集、邻域粗糙集、覆盖粗糙集以及各种多粒度粗糙集等,对复杂的数据系统进行属性约简和决策[4-6]。基于粗糙集理论在处理复杂数据系统上的优势,学者们提出结合粗糙集及其拓展模型对复杂系统进行预处理,降低数据维度,再结合机器学习进行预测。如,结合粗糙集理论及其拓展模型构建的社交链接的预测模型[7]、太阳活动预测模型[8]、痛风预测[9-10]、零件制造过程质量预测[11]等。另外,Zhao等和Lei等基于粗糙集进行属性约简,再分别结合模糊Bandelet神经网络和深度学习对叶轮寿命和建筑能耗进行预测[12-13];Halder等通过构造粗糙模糊分类器对微阵列基因表达数据进行癌症预测[14];Albuquerque等基于粗糙集分类对热带河流水质进行大规模预测[15]。此外,还有直接结合机器学习理论的技术来处理预测问题[16-18]。然而,现有的基于粗糙集理论的预测分析模型存在以下两个方面的局限:
1) 现有的预测分析模型预测的结果缺乏语义信息,存在可解释性不足的局限性,致使进一步决策管理时会产生不信任预测结果的情况。
2) 粗糙集及其拓展模型是从对象的角度来构建,粗糙集中的二元关系度量的是对象之间的相关性,在进行预测时忽略了属性之间的相关性对预测结果的影响,这将导致预测分析模型对多属性系统的预测可能失效。
因此,为了突破现有预测分析模型可解释性不足的局限性,本文试图另辟蹊径,深度融合粗糙集理论,对当前的数据进行强化处理,挖掘数据系统中属性之间的相关性对决策的影响,构建一种全新的具有可解释性的预测分析方法来保障后续的决策管理。
1 面向属性的粗糙模糊集模型
现实情况中,对于多属性系统,属性之间会存在某种关系,这种关系可以反馈到对象上,进而影响决策。因此,本文通过分析属性之间的相关性,构造基于属性的模糊相似度,进一步分析属性之间相关性对对象的影响,进而构建粗糙模糊集模型。基于属性的模糊相似度的定义如下:
Sγ(a,b)=
γ∈[0,0.5)
(1)
其中:U为论域;f(x,a)表示对象x在属性a下的模糊隶属度。然后,基于模糊相似关系进行粒度刻画,其定义为
(2)

(3)
在粗糙集理论中,粗糙集上、下近似将论域U划分为3个区域,即正域、负域和边界域。正域是粗糙集的下近似集,正域和边界域共同构成上近似集。从粗糙决策的角度来看,正域表示接受决策,负域表示拒绝决策,边界域表示延迟决策。只有属于下近似集才可接受的决策被认为是悲观决策,而只要属于上近似集就接受的决策被认为是乐观决策。因此,本文将悲观决策认为是从所有强相关性的属性(入围方案)中选择值(收益)最小的保险决策;乐观决策认为是从所有强相关性的属性(入围方案)中选择值(收益)最大的冒险决策。基于这个角度,可以从所有弱相关性的属性(否决方案)中选择值(收益)最小的决策来定义粗糙模糊集的负域。即
(4)
从粗糙模糊集对数据处理的角度来分析,其下近似和负域可以强化数据之间的区分性,有利于处理互斥类问题,可以用来构建具有可解释性的趋势预测分析模型。
2 可解释性预测分析模型
本文构建的面向属性的粗糙模糊集模型有以下几方面的优势:①从模型构建的角度上考虑了属性之间的相关性,有益于对象的预测分析;②模型本身进行数据处理时能够强化原始数据区分性;③模型对论域的划分是基于各类决策角度的倾向性,能为预测分析提供可解释性。因此,本文将结合面向属性的粗糙模糊集来构建一种具有可解释性的趋势预测分析模型。
模型构建思路如下:将多属性系统看作是一个模糊系统,每个对象是一个模糊集。将粗糙模糊集下近似(悲观决策方案)和负域(否决方案)作为可解释趋势预测的目标函数。为预测某个备选对象的发展趋势,首先,通过训练集训练模糊相似关系,通过聚类方法获得具有强相关性的属性集来刻画粒度结构,再计算备选对象的粗糙模糊下近似和负域;然后,根据相似度或距离等评估方法来计算备选对象与粗糙模糊下近似和粗糙模糊集负域之间的相似度(或者距离);最后,再对相似度或者距离进行评估,进而实现趋势预测的目的,获得可解释性的预测结果。
实现该模型的具体步骤如下:
1) 对数据集进行归一化预处理。
2) 构建训练集和测试集。
3) 基于训练集,从属性的角度计算数据集的模糊相似关系,然后,基于某一水平刻画粒度结构。
4) 计算测试集的粗糙模糊集上近似、下近似和负域。
5) 评估测试集中各个备选对象与粗糙模糊下近似和粗糙模糊集负域之间的相似度(或者距离)。
6) 根据步骤5)计算的结果进行趋势预测。若与粗糙模糊下近似集更相似或接近,则认为趋向于悲观决策方案所在类(保守类所代表的具有可解释性的类别);若与粗糙模糊负域更相似或接近,则认为趋向于否决方案所在类(淘汰类所代表的具有可解释性的类别)。
7) 输出预测结果。
上述是本文提出的可解释性预测分析模型的框架,该框架可对步骤3)~步骤6)进行拓展和优化。即步骤3)中,属性之间的相关性度量,可以采用其他二元关系进行度量;步骤4)和步骤5)中,可以构建其他类型的粗糙集模型,并借助上近似(乐观决策)和下近似(悲观决策)进行可预测模型的构建;步骤6)中,除了直接根据评估值进行判定外,还可以加入超参数,实现3类及以上的可解释性预测分析。
综上,本文提出的可解释性预测分析方法的框架具有可扩展性和广泛的适用性,对不同的预测分析问题如分类或聚类问题,均可处理。
3 实验对比分析
3.1 实验相关设置
为了验证本文提出的可解释性预测分析模型的可行性和有效性,本文将该模型应用于二分聚类的预测分析中。为了便于实验区分和识别,将本文提出的模型命名为ARFC模型,并与现有聚类模型进行实验对比研究,实验相关设置如下:
1) 选用UCI 数据库(https:∥archive.ics.uci.edu/ml/datasets)中的5个数据集进行实验,数据集的描述如表1所示。实验之前需对数据集采用min-max标准化方法进行处理。
2) 采用ARFC模型进行实验的过程中,将数据集按7∶3的比例划分训练集和测试集;且ARFC模型采用余弦距离对备选对象与粗糙模糊下近似和粗糙模糊集负域之间的距离进行评估,以实现可解释性的二分聚类预测。
3) ARFC模型为了获得最优粒度结构下的预测结果,需要对模型中的参数γ和δ进行遍历。
4) 选用了6种聚类算法进行了实验对比研究,分别为:Kmeans++,KFCM,AHC-average,GMM-EM,Apclusterk,Spectral cluster。
5) 采用了聚类有效性指标对各种聚类算法进行性能评估。其中外部指标5个:ACC (标签预测精度),NMI (normalized mutual information),ARI (adjusted Rand index),F值(F-measure),Rand指数 (Rand index)。内部指标5个:KL (krzanowski-lai),Ha (hartigan),Hom(homogeneity),Sep (separation),Wtertra(weighted inter-to intra-cluster ratio)。所有指标中,除KL、Ha两个指标的值越小,表示聚类性能越好,其余指标值越大,则表示聚类性能越好。
3.2 实验结果与分析
表2为各个数据集下,采用ARFC模型进行聚类预测时,对模型中的参数γ和δ进行遍历后获得的最优粒度结构。
表3~表12是各个数据集在不同聚类算法下获得的聚类有效性评价指标的结果,其中,AFRC模型的结果是基于最优粒度结构获得的。图1~图10是与表3~表12相对应的网状图,图形越接近五边形(图形面积越大)代表聚类效果越好。其中,由于KL、Ha两个内部指标的值越小,表示聚类性能越好,为了便于比较,图6~图10中的KL和Ha两个指标是对表8~表12中的KL和Ha两个指标中的数据进行了反比例处理而构图的。
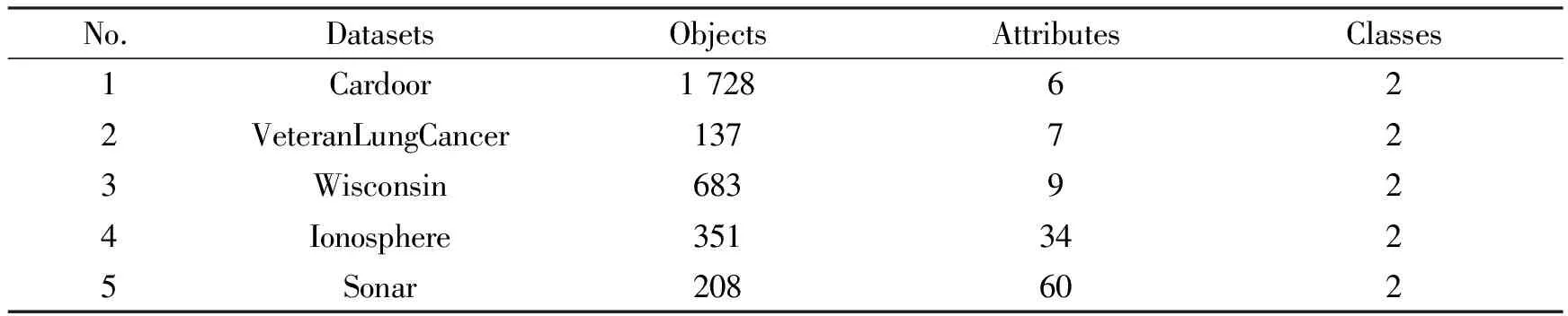
表1 数据集的详细描述Tab. 1 Detailed description of data set

表2 AFRC模型在各数据集下的最优粒度结构Tab.2 Optimal granularity structure of AFRC model under each datasets
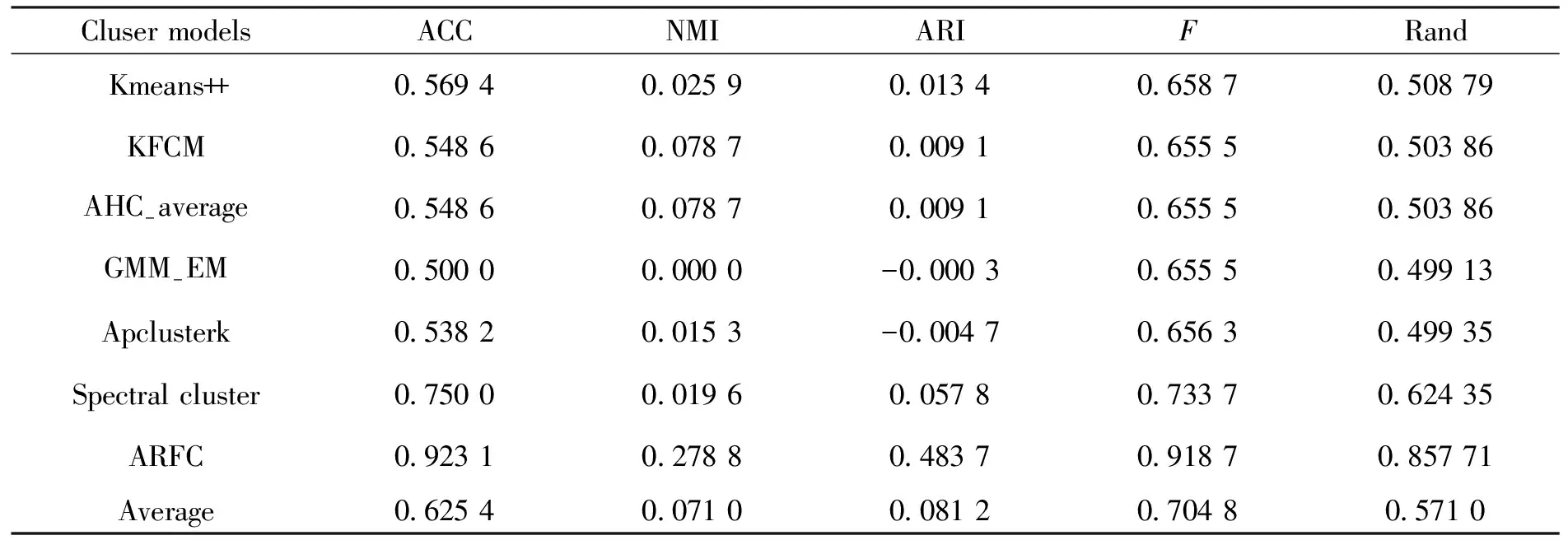
表3 各聚类算法下Cardoor的外部指标结果Tab.3 External index results of Cardoor under various clustering algorithms

表4 各聚类算法下VeteranLungCancer的外部指标结果Tab.4 External index results of VeteranLungCancer under various clustering algorithms
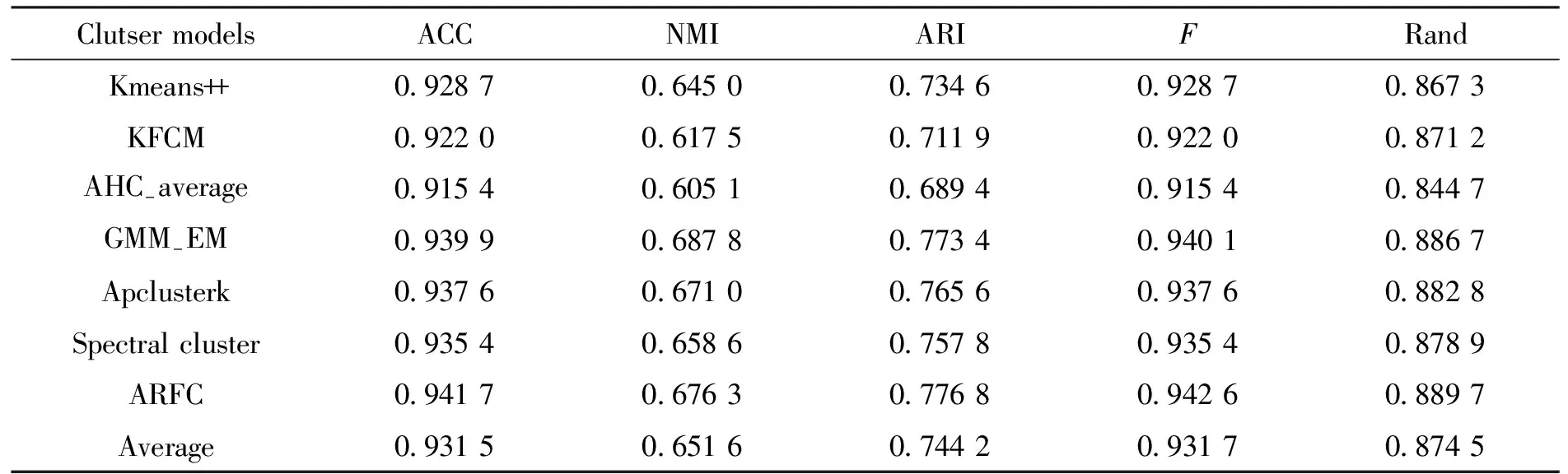
表5 各聚类算法下Wisconsin的外部指标结果Tab.5 External index results of Wisconsin under various clustering algorithms
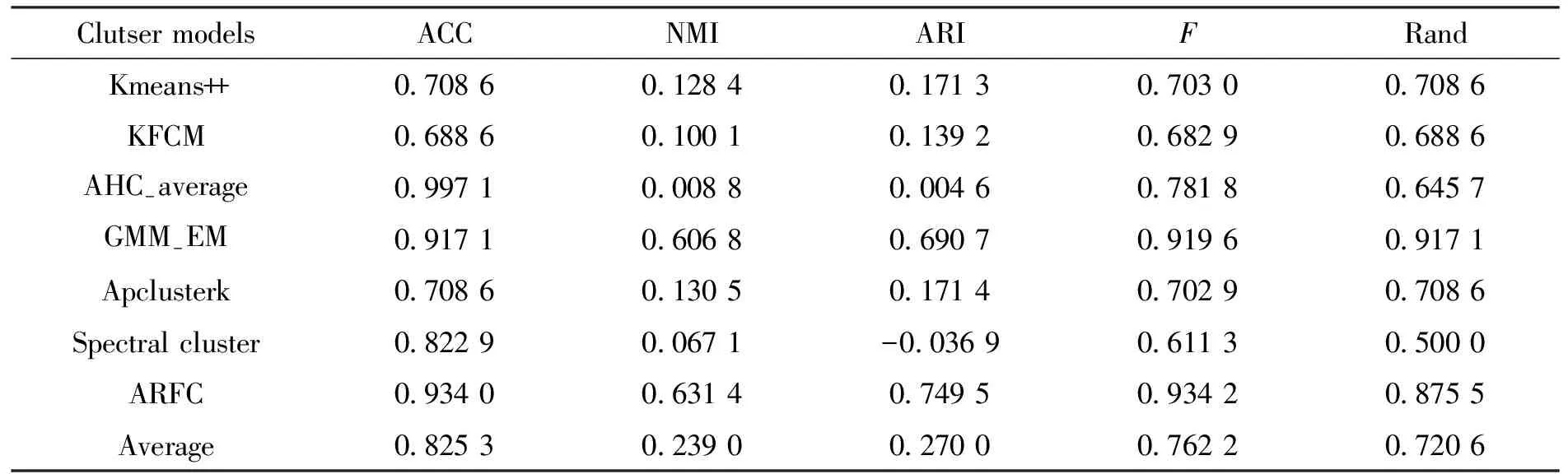
表6 各聚类算法下Ionosphere的外部指标结果Tab.6 External index results of Ionosphere under various clustering algorithms

表7 各聚类算法下Sonar的外部指标结果Tab.7 External index results of Sonar under various clustering algorithms

表8 各聚类算法下Cardoor的内部指标结果Tab.8 Internal index results of Cardoor under various clustering algorithms

表9 各聚类算法下VeteranLungCancer的内部指标结果Tab.9 Internal index results of VeteranLungCancer under various clustering algorithms

表10 各聚类算法下Wisconsin的内部指标结果Tab.10 Internal index results of Wisconsin under various clustering algorithms
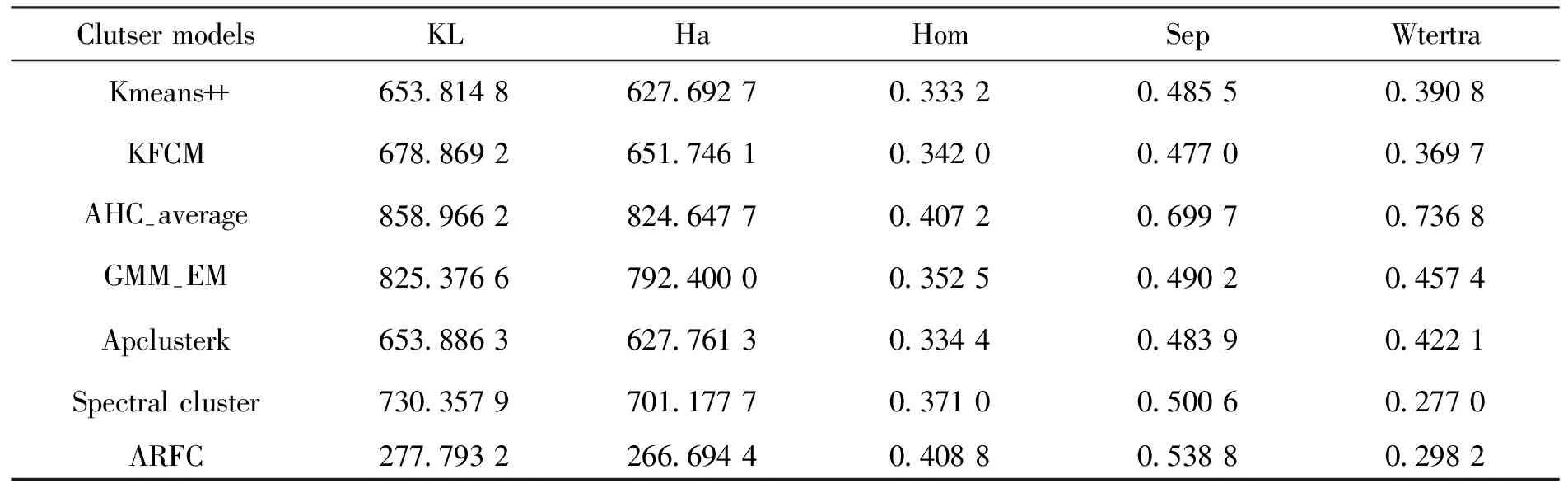
表11 各聚类算法下Ionosphere的内部指标结果Tab.11 Internal index results of Ionosphere under various clustering algorithms

表12 各聚类算法下Sonar的内部指标结果Tab.12 Internal index results of Sonar under various clustering algorithms

图1 Cardoor的外部指标网状图Fig.1 External indicator network of Cardoor

图2 VeteranLungCancer的外部指标网状图Fig.2 External indicator network of VeteranLungCancer

图3 Wisconsin的外部指标网状图Fig.3 External indicator network of Wisconsin

图4 Ionosphere的外部指标网状图Fig.4 External indicator network of Ionosphere

图5 Sonar外部指标网状图Fig.5 External indicator network of Sonar

图6 Cardoor的内部指标网状图Fig.6 Internal indicator network of Cardoor

图7 VeteranLungCancer的内部指标网状图Fig.7 Internal indicator network of VeteranLungCancer

图8 Wisconsin的内部指标网状图Fig.8 Internal indicator network of Wisconsin
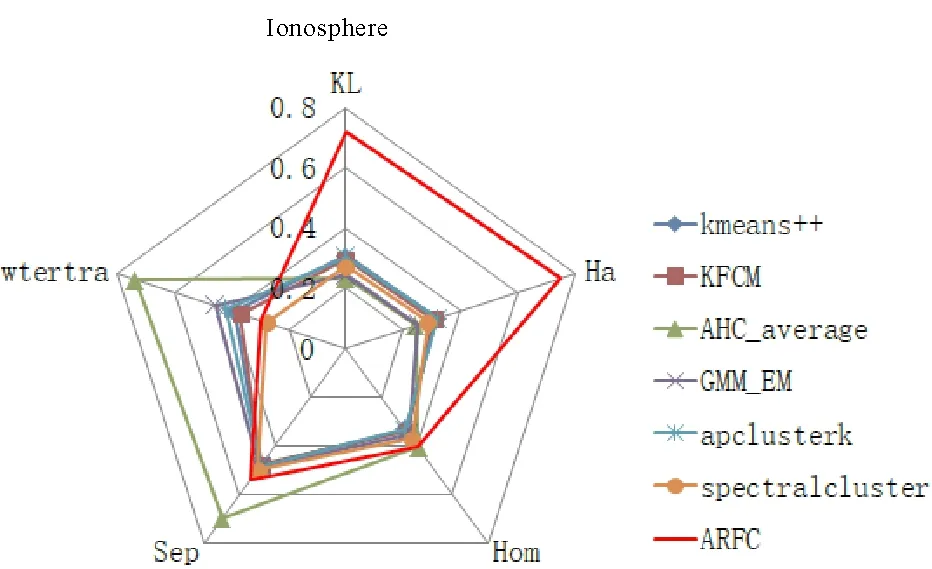
图9 Ionosphere的内部指标网状图Fig.9 Internal indicator network of Ionosphere

图10 Sonar的内部指标网状图Fig.10 Internal indicator network of Sonar
聚类外部有效性指标结果可以看出,本文提出的预测分析模型具有明显的优势。从内部有效性指标结果来看,数据结果整体往KL和Ha两个指标偏,反映出本文提出的模型与其他模型存在本质上的差异性,这是由于本文模型深度融合了粗糙集理论进行预测分析。换个角度来说,在一定程度上表明本文提出的预测模型具有一定的创新性。其创新性主要体现在以下两个方面:
1)基于属性之间的相关性对预测分析的影响,本文从对象的角度来度量属性之间的相关性,进而构建了属性间模糊相似关系;
2)从属性的角度构建粗糙模糊集模型对数据进行强化处理,进一步从粗糙决策的角度,构建了具有可解释性的目标预测函数,进而实现可解释性预测。
4 结语
本文提出了一种全新的、具备可解释性的预测分析模型。该模型深度融合了粗糙集理论,从属性的角度构建了粗糙模糊集模型来强化原始数据区分性,再基于粗糙决策的角度设计具有可解释性的目标函数,进而评估预测对象与目标函数,来实现可解释性预测分析的目的。本文的研究为预测分析理论与方法提供了创新性的思路和方向。从模型构建的框架来看,该模型具有广泛的适用性,可以进一步拓展和改进不同领域可解释性预测分析问题的处理,对研究复杂系统的预测分析和决策管理具有重大意义。

