鱼类死亡系数估算方法及应用研究进展

赵长浩，花传祥,2，朱清澄,2，石永闯，汪金涛,2,5,6,7，李 非

(1.上海海洋大学 海洋科学学院，上海 201306； 2.国家远洋渔业工程技术研究中心，上海 201306； 3.中国水产科学研究院 东海水产研究所，渔业资源遥感信息技术重点开放实验室，上海 200090;4.中国水产科学研究院 东海水产研究所，农业农村部东海与远洋渔业资源开发利用重点实验室，上海 200090； 5.大洋渔业资源可持续开发教育部重点实验室，上海 201306； 6.农业农村部大洋渔业资源环境科学观测实验站，上海 201306； 7.农业农村部大洋渔业开发重点实验室，上海 201306)

死亡系数是影响鱼类群体数量变动的关键因素(补充、生长、死亡)之一[1]，同时是渔业资源评估的重要参数，它反映个体从种群中消失的快慢[2]。在研究鱼类种群动态、渔获量预测、捕捞对渔业资源数量变动的影响和制定渔业管理措施时，均需要对死亡系数进行估算，如果死亡系数未知就难以建立种群动态模型，同样难以估计可持续的捕捞率或其他有用的管理参数[3]。死亡系数可分为自然死亡系数(M)、捕捞死亡系数(F)和总死亡系数(Z)。自然死亡系数是由自然原因(如捕食、疾病和衰老等)造成的某个鱼类种群单位时间内的相对死亡率；捕捞死亡系数，顾名思义，是由于捕捞造成的鱼群相对死亡率；捕捞死亡系数和自然死亡系数之和为总死亡系数[4],可表示为：Z=M+F。

目前，死亡系数的估算方法被分为两大类[5]，一类是利用标记或渔获产量数据的直接估算，另一类是基于生物学指标的间接估算。虽然国内外学者对鱼类死亡进行了较多的研究，但尚未有一种方法能够对每一个物种进行准确估计，也没有一种方法能足够精确地用于种群估算，较多的模型表现较差，且存在极大的不确定性[6]。研究表明，利用放流或渔获量数据的直接法去估算鱼群死亡情况是十分困难的，虽然有学者认为可利用遥感和标记放流法对鱼群的死亡情况进行估算，但这些方法并不具有实用性[7]，所以在鱼类死亡系数估算中主要应用基于生物学指标的间接方法。

国内对鱼类死亡系数估算方法的研究和报道较少，通常是利用基于生活史参数的经验公式进行估算，其中以Pauly经验公式[8]最为常见。笔者根据生活史分析、实际种群分析法和渔获曲线法分别对国内外自然死亡系数、捕捞死亡系数和总死亡系数的估算方法进行概述，分析现有估算方法存在的问题，比较不同方法之间的差异，提出改进意见，以期为渔业资源评估与管理提供科学依据。

1 以生活史参数估算自然死亡系数

通常自然死亡系数与鱼类生活史密切相关，基于生活史参数的估算法所描述的是自然死亡系数与各种生长参数之间的关系，根据不同的生长参数数据，利用不同的计算方法进行关系推导，即可得到基于生活史参数的关系式，此类基于众多生活史参数而建立的估算方法，具有以下优点：(1)仅需要少量的渔业数据；(2)可有效地在宏观层面上观察出种群的变动趋势。但因为它们对任何种群的鱼只产生单一的自然死亡系数，且准确性较差，此外，与回归分析法相比并没有任何优势，因此，当数据不够完全时，只能粗略地估算自然死亡系数，而在利用生活史参数估算过程中，以经验法最为常见[9]。

至今，自然死亡系数主要根据不同结构的模型进行估算。对模型进行选择时，主要根据以下几个步骤：

(1)从理论和实际出发，假设一种有效并且合适的模型类别；

(2)利用参数分析模型筛选模型，选择最适用的模型；

(3)对最适模型的参数进行估算；

(4)对模型进行验证，若模型适用，则利用其进行估算；反之，再次从步骤(2)开始[10]。

基于不同的生活史参数及生物学特征，目前常用的估算自然死亡系数的方法主要有以下几种。

1.1 Pauly法

Pauly[8]描述了一种常用的估计自然死亡系数的间接方法，他将自然死亡系数与von Bertalanffy生长参数和平均环境温度联系起来，这种方法假定鱼的大小(以长度或质量衡量)与自然死亡系数之间存在一种较弱的相关关系，环境温度的加入使这种关系变得显著。Griffiths等[11]将175种鱼类(包括海水鱼类和淡水鱼类，分布由赤道至极地)的估算结果进行平均化建立经验公式，结果显示，自然死亡系数与环境温度为正相关，因为生活在较温暖水域的鱼种比生活在较冷水域的同类鱼种有更高的死亡率。

针对该模型固有的局限性[如不能估计软体动物和甲壳类的自然死亡系数，对于鲷鱼、石斑鱼(Epinephelus)等特定鱼种的估算可能存在偏差]，Calderon-Aguilera等[12]通过使用修正系数0.8解决经验公式估算集群鱼类自然死亡的问题，该方法因其参数的易得性以及计算方法的简易性而被广泛应用。目前Pauly经验公式是我国近海鱼类种群自然死亡系数估算最常用方法之一，小黄鱼 (Larimichthyspolyactis)[13-15]、带鱼 (Trichiurusjaponicus)[16-17]、黄鲫 (Setipinnataty)[18-19]、短尾大眼鲷 (Priacanthusmacracanthus)[20-22]、花斑蛇鲻(Sauridaundosquamis)[23]、刺鲳(Psenopsisanomala)[24-25]、竹鱼(Trachurusjaponicus)[26]、二长棘犁齿鲷 (Evynniscardinalis)[27-28]等自然死亡系数估算均应用该经验公式。

1.2 Griffiths和Harrod法

Griffiths等[11]以Pauly法为基础，对自然死亡系数与环境温度的关系进行研究，并证实了Pauly[8]的结论，即死亡系数与生长和温度有关，生长参数K是主要的预测变量。同时还发现，生活在相近水层的鱼种和生物学特征相仿的鱼种间有着相似的死亡系数，这一发现与Pauly[8]一致。这种情况与生活习性有关，因为死亡速度随食物供应而变化，而食物供应又随营养水平和可获得性而变化，随着水层深度的增加，食物的可获得性会下降[29]。

Griffiths等[11]对鲈鱼、珊瑚礁鱼类、底栖鱼类和中上层鱼类的自然死亡系数进行估算，得到其死亡系数分别为0.11、0.42、0.18和0.25，而使用Pauly法得到的大部分鱼类死亡系数约为0.2，可见两种估计方法所得结果大体相同，但对于特殊物种(如鲈鱼、珊瑚礁鱼类等)所得结果差异较大[6]。

1.3 Gislason法

Gislason等[30]对Pauly模型进行分析并提出了改进。在对175种不同鱼群的163套渔业数据进行分析后，发现自然死亡系数不仅与渐进长度(L∞)和生长参数K相关，而且与体长(L)也显著相关。利用Arrhenius方程来描述温度对自然死亡系数的影响，发现温度与自然死亡系数无显著相关性，并且当移除温度因素后，方程总的拟合度变化甚小，只是其他参数的系数发生变化。

1.4 Charnov法

Charnov等[31]对Gislason等[30]预测海洋鱼类自然死亡系数的经验方程和数据进行重新分析，在一项对北海鱼类群落的建模研究中发现，体长、渐进体长对自然死亡系数的估算无显著差异，自然死亡系数的估算既可以用体长表示，也可以用渐进体长表示，并且与Denney等[32]的观点一致，即自然死亡系数与渐进体长负相关。

虽然该方法具有在生活史理论中更容易理解的优势，但对相关体长参数的错误估计会进一步增加自然死亡系数的不确定性，但从回归分析变化的角度来看，其输出估计值的95%置信区间从估计值的1/4扩大到4倍，此方法是基于回归的估计方法中相对可靠的，而其他模型的估算能力相对较弱[33]。

1.5 Peterson-Wroblewski和McGurk法

许多试验结果证实，鱼的自然死亡系数与其体质量(m)密切相关，并存在一定的线性关系，利用体质量、生长参数K等参数对种群自然死亡系数进行回归预测具有良好的效果[34-36]。Peterson[37]量化了这种关系，假设鱼群的自然死亡由捕食所致，基于体质量对自然死亡系数提出了异速增长模型，综合各种生长环境，指数的值约为-0.25，这一取值在之后的研究中得到了理论和经验的支持[38]。有学者提出，Peterson-Wroblewski法以小型浮游生物到大型鲸类的体质量关系为基础，在数据分析时容易引起较大误差[39]，这一结论得到McGurk[40]的支持。

1.6 詹秉义法

已有研究证实，鱼类自然死亡系数与最大年龄负相关[41]。Tanaka[42]基于这一关系对自然死亡系数和鱼类最大年龄进行回归分析，詹秉义等[3]在此基础上利用黑姑鱼(Atrobuccanibe)、日本沙丁鱼(Sardinopsmelanostictus)和太平洋鲱(Clupeapallasiissp.pallasii)等9种鱼类的最大年龄数据进行回归分析，该方法后被应用到我国东海绿鳍马面鲀(Thamnaconusmodestus)[43]和长江鲥(Tenualosareevesii)[44]的资源量估算。

1.7 Alverson法

Alverson等[45]假设，没有外界捕捞的情况下，鱼群是等密度增长并且符合生长曲线，其将鱼群达到最大生物量时的年龄(tmb)作为估计死亡系数的指标，对63种不同的鱼类进行分析，发现tmb=0.38tmax(tmax为最大年龄)，并得出自然死亡系数和生长参数K及最大年龄之间的表达式。虽然该方法在短寿命、快速生长鱼类的自然死亡系数估计中结果往往偏大，如凤尾鱼(Coiliamystus)等，但因其所需信息量小，在之后的鱼类[如灯笼鱼、蓝点马鲛(Scomberomorusniphonius)等]自然死亡系数的估计中广泛应用[46]。

1.8 Gunderson和Dygert法

r-K选择理论是生态学上有关生物体如何权衡后代的数量与质量的理论，是检验海洋鱼类自然死亡系数、雌性性腺发育指数(GSI)、成熟年龄、寿命和von Bertalanffy生长参数之间相关性的基础[47]。1980年，Gunderson[48]假设雌性在繁殖过程中投入的能量与自然死亡系数之间有很强的相关性，并利用r-K选择理论对10种北海硬骨鱼类进行研究，提出了新的自然死亡系数与雌性性腺发育指数的关系式。1988年，Gunderson等[49]将渔业数据扩展到20种北海硬骨鱼，所得结果均与r-K选择理论一致，即雌性鱼类性腺发育指数与自然死亡系数的相关性最高，但有学者提出此方法若用于卵生或卵胎生的物种，估算结果可能会更好[50]，并在白斑角鲨 (Squalusacanthias)[51]和澳大利亚尖鼻鲨(Rhizoprionodontaylori)[50]自然死亡系数估算中得到应用。

1.9 Jensen法

Jensen[52]通过平衡生存和繁殖的关系，根据Pauly[8]自然死亡系数估算的数据进行分析，发现自然死亡系数与生长参数K有显著的关系，且自然死亡系数与生长参数K成正比，这一结论得到众多学者支持[53-55]。Pauly[8]分析的核心是假设所分析的数据点和变量是相互独立的，虽然该分析没有考虑到系统发育及多种群的非独立性，但结果与Pauly[8]分析结果M=1.6K接近，且与Gulland[56]的观点一致(硬骨鱼类的自然死亡系数通常在K和2K之间)，该结论在密西西比铲鲟(Scaphirhynchusplatorynchus)[57]和沙重牙鲷(Diplodussargus)[58]等物种的资源估算中得到应用。

1.10 Rikhter和Efanov法

Rikhter等[59]认为，自然死亡系数与鱼群达到50%成熟时的年龄(tm50)相关，并以14种高纬度鱼类作为研究对象，建立两者之间的关系。该方法后被Efitre等[60]用到乌干达火山湖中吉利慈鲷(Tilapiazillii)群体的自然死亡系数估算。由于估算时对各生长参数要求较为严格，分析时易受到基于回归方法的影响，并且50%成熟时的年龄难以估算，因此此方法被应用的较少。

以上方法的汇总及在鱼类中的应用见表1、表2。

表1 自然死亡系数估算方法总结

表2 利用不同方法估算鱼类自然死亡系数

除上述几个常用的估算方法外，Roff[61]、Djabali等[62]、Jennings等[63]、Cubillos等[64]、Alagaraja[65]、Hoenig[66]等对自然死亡系数也进行了研究，并提出各自的看法与观点。

由于持续的过度捕捞及环境污染，鱼类种群衰退愈加严重，大部分种类出现个体小型化、低龄化现象，加之完善的标志回捕体系没有建立，使得标志回捕等方法在自然死亡系数的估算中难以实施，因此在鱼群资源量估算及自然死亡系数估算时，使用基于生活史的估算方法最为广泛[1]。渔获数据的差异及模型自身的偏差使任何估算方法均存在一定的不确定性，模型不同所需参数也不同，且参数之间存在不同的误差，导致模型估算结果不具有可比性[67]。由于自然死亡系数易受种群内部及外部因素的影响，因而一直是资源量估算中的难点[68]，所以，对其进行估算时，应充分考虑估算模型的不稳定性，利用多个估算值生成一个包含估算结果的置信区间来替代一个简单数字将是更好的选择。

2 以实际种群分析估算捕捞死亡系数

实际种群分析(VPA)，又称有效种群分析和现实种群分析，在Fry[69]研究的基础上，Gulland[70]提出并应用，之后得到Jones等[71-72]学者的检验。Pope[73]对实际种群分析的灵敏性进行分析，并简化Gulland[70]的方法，使实际种群分析中的非线性计算方法转换为线性模型，建立了股分析法。两种方法均可以利用年龄和体长对鱼群数量进行估算，通过对某一年份实际种群的各世代及单位捕捞努力量渔获量进行逆运算分析，估算过去各年份实际种群的资源数量和捕捞死亡系数[74]，股分析法相对于实际种群分析来说,估算过程变得更加简单。

目前，实际种群分析和股分析法已经成为估算渔业资源量和捕捞死亡系数以及预报未来资源量的经典方法之一，其原因是[3]：

(1)避免使用难以测量和收集的捕捞努力量，降低了对所需数据的要求；

(2)由一个世代的最高年龄组开始逆运算各年龄组的捕捞死亡系数和资源数量、资源生物量，会逐渐提高估算的准确性；

(3)不需要鉴定研究对象年龄及其组成资料，从而扩大该方法的使用范围。

在进行实际种群分析估算时，具体运算步骤可分为3种不同情况分别处理：(1)已知渔获尾数Ci、自然死亡系数Mi、捕捞死亡系数Fi；(2)已知渔获尾数Ci、自然死亡系数Mi、资源数量ni；(3)已知渔获尾数Ci、自然死亡系数Mi、翌年资源数量ni+1，主要通过下式进行运算[3]：

(1)

(2)

ni+1=nie-(Fi+Mi)

(3)

估算前需假设各年龄段的自然死亡系数均相同，根据样品的年龄组成和总渔获量计算出各年龄段的渔获尾数，然后利用生活史、捕捞曲线等方法对自然死亡系数、总死亡系数进行粗略估算(或假设捕捞死亡系数为一固定值，通常取0.5)[75]。在已知死亡系数与渔获量的情况下，采用反复迭代的方法估算历年的资源量，反之可对历年死亡系数进行估算，以此类推，直至将历年各年龄组捕捞死亡系数、资源数量全部推算出为止。

实际种群分析与股分析是渔业资源估算与捕捞死亡系数估算的经典模型之一，被广泛应用到东海及长江口区域日本鲭(Scomberjaponicas)[76]、东海绿鳍马面鲀[77]、长鳍金枪鱼(Thunnusalalunga)[78]、太平洋鲱[79]等多种鱼群的估算中。Maunder等[80]认为，如果能够获得长期的年龄结构渔捞数据，采用实际种群分析估算是最佳的方法。但该方法忽略了渔业资源和捕捞数据的误差及不同年龄组间捕捞死亡系数的相关性，与传统的估算方法相比，对数据的要求非常严格，需要渔获量数据准确无误，并需要特殊的方法来设置各世代最大年龄鱼的捕捞死亡系数或资源量[81]。使用实际种群分析进行资源评估，如果捕捞死亡系数特别大时，该类模型具有较好的评估效果[82]，为协调参数给实际种群分析模型造成的不确定性，许多学者提出各种实际种群分析的调谐法，如明智平均法(JAM)[83]，Laurec-Shepherd法(LS)[84]、混合法(Hybrid)[85]。

目前，我国利用实际种群分析模型对渔业进行估算相对较少，由于所需资料不全、所用参数不准确等原因，分析结果仍存在一定误差，为了更好地使用实际种群分析模型，应根据实际种群分析的需要建立长期规范的全面调查,收集合适的数据[86]。

在对捕捞死亡系数进行估算上，除实际种群分析法外，水声学调查法[87-88]、鱼卵调查计数法[89]、扫海面积法[90-92]、标记放流法[93]等多种方法也被提出，但分别因品种鉴别难度大、只能鉴定鱼卵和仔稚鱼且花费高、精确度低、假设与实际完全不符等较少在捕捞死亡系数估算中使用。

3 捕捞曲线估算总死亡系数

20世纪对渔业死亡系数的研究，起初将北海拟鳙鲽的渔获量分成间距相等的小组，每一小组的频率对数连成一条曲线，曲线的下降部分表示为总死亡系数[94]，后有学者将渔获量N、年龄t、大小与曲线相结合起来所绘制的曲线，即为渔获量曲线。目前捕捞曲线可分为两类，即：转换体长渔获量曲线(LCC)，转换年龄渔获量曲线(ACC)。公式如下：

转换体长渔获量曲线：ln(N/ti)=a+bti

(4)

转换年龄渔获量曲线：ln(Ni)=a+bti

(5)

在估计渔业死亡系数时要做以下假设[95]：

(1)各年龄组的残存率是相同的；

(2)总死亡系数在符合线性函数的年龄组中是恒定的；

(3)死亡系数不随时间而变化；

(4)鱼群增长在两年内是固定的；

(5)渔具影响对所有年龄组的鱼类都是一样的。

曲线由3部分构成：上升的左枝，圆顶的中间部分和下降的右枝(图1)[96]。其中红色虚线代表理想的捕鱼量曲线，即所有年龄段的鱼都完全纳入渔业。

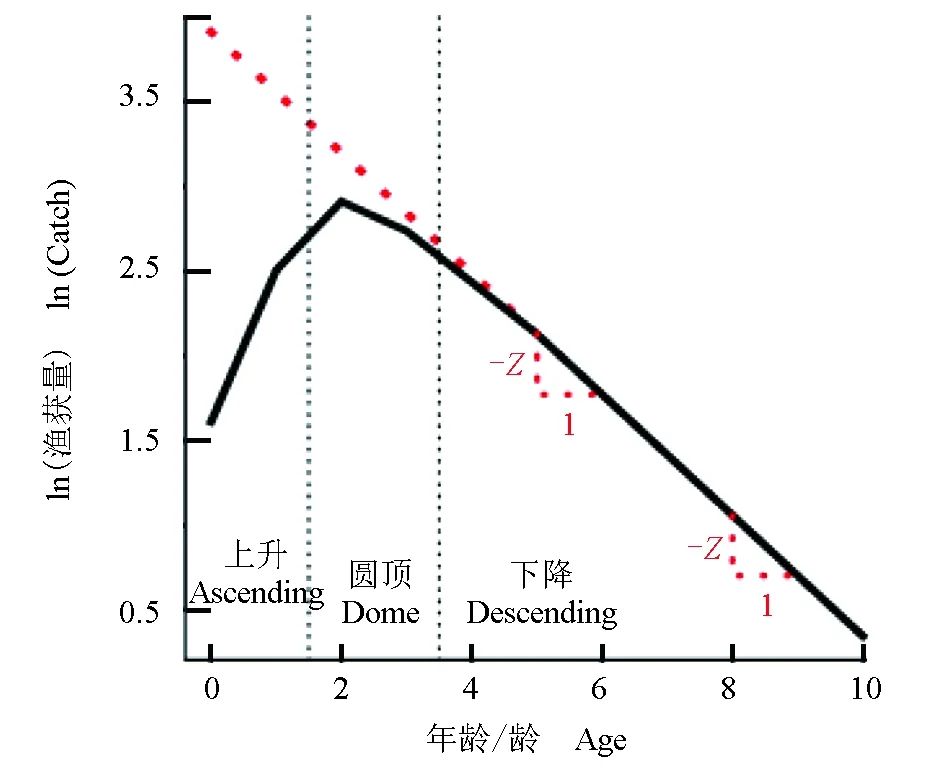
图1 渔获量曲线Fig.1 Catch curve

渔获量曲线的上升左枝和拱顶代表了所用渔具不能完全捕获的相应年龄组[97]，曲线的右枝可用于死亡系数的估算。由于捕捞渔获量与补充量成一定比例，在总死亡系数与补充量均比较稳定的情况下，可通过随机采样获得的渔获量曲线对总死亡系数进行估计[96]，所得总死亡系数即为直线斜率的负值，或线性回归方程回归系数的负值。

体长结构曲线早在20世纪初被提出，之后逐渐被年龄结构的渔获曲线所取代，然而对年龄的测定是一个费时费力的过程，在许多水生动物(如鱿鱼、甲壳类、虾和各种热带鱼)中，年龄的测定是非常困难的，甚至是不可能的[98]。直到20世纪90年代，Pauly[8]根据年龄可用von Bertalarffy生长方程转换为体长的理论，将基于年龄的曲线转换为体长曲线，并将其命名为长度转换渔获曲线，此后该方法才得到关注。

在利用长度转换渔获曲线对总死亡系数进行估算时，需根据具有代表性的鱼群数量和生长所需时间进行制图，并根据曲线右枝下降点的大致趋势对总死亡系数进行粗略估计。在总死亡系数的估算中，点的选择以“未全面补充年龄段和接近渐进体长年龄段不能用于回归”为原则[99]，直到总体在样本中得到充分表示，各点不显著偏离估计的回归线，此时所得到总死亡系数的估计值是相对准确的[100]，但有两种情况可能是例外[101]：(1)随着鱼群年龄的增大，所捕获鱼的比例逐渐减少，残存率随年龄增大而增大，因此在这种情况下，不能或不能完全反映出渔获比率，所估计的总死亡系数也会有误差；(2)每年鱼群的补充量不确定的增加或减少也会改变总死亡系数。

当然，要对总死亡系数进行更准确的估算，除依靠渔获量曲线外，还可采用捕捞努力量渔获量(CPUE)法[3]、B-H法[109]、自然死亡系数与捕捞死亡系数相加法[4]等，但由于长度转换渔获曲线法最为常见，因此笔者只对其进行概述。

4 存在的问题和建议

死亡系数在不同鱼群间是不同的，在时间与空间上也是可变的，根据鱼类生命周期可分为3个阶段，即初始、稳定、衰老，死亡系数在以上3阶段中呈“U”型变化[110-111]。自然死亡系数与捕捞死亡系数是截然不同的，由疾病、捕食、环境因素引起的自然死亡出现在鱼群的整个生命周期，而捕捞死亡主要出现在鱼群的可开发阶段。一直以来，对自然死亡的研究以鱼群的开发阶段为主，未对鱼群的初始阶段进行分析，该阶段为鱼群生命周期的一部分，并且自然死亡系数较高，这也是大多方法估算误差较大的原因之一[112]。因此，随着估算方法的不断创新、研究的不断深入，自然死亡系数的估算不应局限于鱼群的开发阶段，而要贯穿鱼的整个生命周期。

死亡系数估算结果的误差对资源量估算的影响是不容忽视的，不仅会对物种资源产量产生错误估计，还会导致鱼群动态随时间的变化趋势不准确。随着计算机技术的发展，各种模型逐渐多样化、复杂化，由于不同模型对数据的要求不同，数据质量又是决定估算结果可信度的主要因素，导致每种方法估算结果之间不具有可比性[67]。在提高数据质量的同时,不应仅从估算结果判断模型的好坏,应进一步分析模型所研究对象的特征及数据的可信程度,减小估算误差。

目前，对渔业死亡系数的估算主要以单物种模型为主，局限性较大[81]。为了更好地了解鱼群动态及渔业资源情况，在以后的研究中应使用多物种模型，并参考鱼类行为学理论知识，及引入假设的不确定性，以确保估算的准确性。

5 总结与展望

在今后的死亡系数研究中，不仅应该把更多的注意力放在估算平均的死亡系数上，还应该关注其随鱼群年龄及规格的变化，只有当各死亡系数经过充分研究，并且在种群中得到更好的认识，才能从本质上提高估算的准确性。许多学者已经意识到死亡系数和各种预测因子之间的关系在种群之间是不同的，但是缺乏充分的先验估计以至于在估算时可能出现严重误差。多数鱼类在躲避捕食者的行为上消耗大量能量，因此可以预期，这些鱼类的死亡系数较低，然而这些因素都被目前可用的估算模型所忽略[9]。

在对死亡系数进行估算时，首先需要对模型的种类进行选择，当对一个群体早期进行估算时，间接方法较广泛的被使用，不同的模型输出不同的结果，但在某些情况下，方法之间几乎没有区别，如Simpfendorfer[113]对灰鲸(Eschrichtiusrobustus)死亡系数的估算使用了5种不同的方法，所有的结果为0.081～0.086。另外，不同方法的估计值可能差异很大，如Simpfendorfer[50]对澳大利亚尖鼻鲨死亡系数的估算使用了7种方法，发现估算值为0.56～1.65。由此可见，我们需要将估算变得更加精密、准确。直接法将提供更加准确的结果，与间接法不同，直接估计需要对特定物种采取抽样，以确保得到满意的结果。在直接法中，标记回捕法估算效果较好，但受回捕障碍、标签脱离等因素的影响，往往估算结果误差较大[114]。在标记回捕数据难以获得的情况下，可选择捕捞曲线方法，捕捞曲线可以产生准确的结果，但是数据必须满足几个假设条件(1.3)。

渔业资源的评估是开展渔业管理的重要前提，而各种模型是资源评估的主要手段，模型所估算的结果可作为制定渔业管理对策的重要依据。在过度捕捞及环境污染的影响下，渔业资源衰退愈发严重，各国越来越注重资源的合理开发和利用，因此对掌握渔业资源状况显得尤为重要。鱼类死亡系数的估算不仅是渔业资源估算的重点，更是难点。我国对死亡系数的研究相对较晚且不够深入，在实际应用中主要依据以上几种典型的经验公式及方法，虽然我国学者在方法创新与参数分析方面取得一定进展，但要想估算出准确无误的死亡系数，仍然面临巨大的挑战。为了更好地了解渔业资源状况，对现有的估算方法进行深度的研究，克服估算方法的局限性及开发新的估算方法与设备已成为当下的关键选择。