基于Kriging模型和提升小波变换的随机模型修正*
吴雨程, 殷 红, 彭珍瑞
(兰州交通大学 机电工程学院,兰州 730070)
引 言
近年来,模型修正方法的研究已经取得重大发展,在机械、土木和航天等领域逐步成为研究热点.但是当前大多数的模型修正方法属于确定性方法,没有考虑到结构参数和响应的不确定性,导致其工程应用价值发挥不充分.工程问题中的不确定性主要为结构装配带来的不确定性、材料参数与几何参数的不确定性、测量数据的不确定性和环境噪声,因此不确定性模型修正方法的研究是非常必要的[1].随机模型修正方法属于不确定模型修正方法,可以减小实测数据与预测的随机响应之间的误差,因此随机模型修正具有重要的意义[2-3].
多年来,国内外学者对随机模型修正方法进行了深入的研究.方圣恩等[4]将随机模型修正过程分解为确定性修正过程,构造优化反演过程来求得各个样本所对应的参数值.Deng等[5]通过构建代理模型,将距离函数作为标准来衡量参数的相关性,从而进行随机模型修正.万华平等[6]提出了采用引入DRAM算法的MCMC方法进行随机模型修正.Zhai等[7]将改进的响应面模型与Monte-Carlo方法相结合进行随机模型修正.陈喆等[8]研究了考虑试验模态参数不确定性的有限元模型修正方法.Jalali等[9]利用Bayes识别方法对连接模型参数中的不确定性进行识别.Zhao等[10]提出了欧氏距离和巴氏距离的平均距离不确定性度量标准,用来进行不确定性模型修正.邓振鸿等[11]提出了基于近似Bayes计算的近似似然函数,并将其作为目标函数应用于H型非对称梁的有限元模型修正.由上述文献可知,将模态参数或频响函数作为响应是目前随机模型修正的常用方法,而多阶模态的测量、频响函数频率点的选取会影响模型修正的效率.
在上述背景下,本文提出了一种基于Kriging模型和提升小波变换的随机模型修正方法.首先,对加速度频响函数(acceleration frequency response function, AFRF)进行提升小波变换,提取近似系数表征原AFRF.其次,抽取训练样本作为Kriging模型的输入,对应的近似系数作为输出,构建Kriging模型.对蝴蝶算法进行改进,将其应用于Kriging模型相关参数的寻优中.最后,利用Wasserstein距离来构造一个优化反问题,通过鲸鱼优化算法对待修正参数的均值进行求解.通过二维桁架和三维桁架验证了所提方法的可行性.
1 Kriging模型的构造
1.1 Kriging模型
Kriging模型是一个基于随机过程的代理模型,对非线性函数具有较好的近似和误差估计功能.模型包含线性回归部分和非参数部分[12]:

式中, β=[β1β2···βp]T为 回归模型系数;f(τ)=[f1(τ)f2(τ)···fp(τ)]T为回归函数;z(τ)为服从正态分布N(0,σ2)的随机分布,其协方差为

其中,E(τi,τj)是对角元素任意两个观察点之间的相关函数.其表达式如下:

建立Kriging模型时需要训练模型参数,一般采用最大似然估计.似然函数如下:
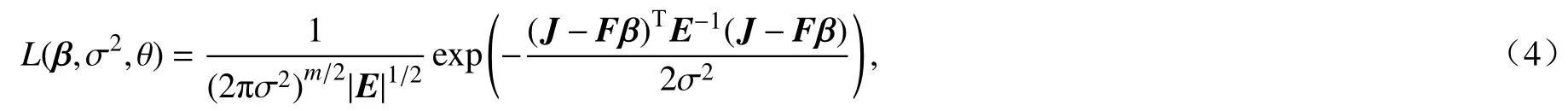
式中,|E|为相关矩阵的行列式;J为样本点响应组成的列向量;F为样本点向量组成的矩阵.β和 σ2的最优值可解析为

由式(5)可看出, σ2和 β均 为 θk的 函数,那么相关参数 θk即为Kriging模型中的唯一未知数,决定着Kriging模型的精度.本文采用上述性能较优的LBOA对相关参数 θk进行寻优,保证构建的Kriging模型具有较高的精度.
1.2 Lévy flight蝴蝶优化算法
1.2.1 蝴蝶优化算法
蝴蝶优化算法(butterfly optimization algorithm,BOA)是Arora模拟蝴蝶觅食过程提出的自然启发式算法[13].该算法中,假设每只蝴蝶散发一定强度的香味,区域内的其他蝴蝶感知到香味并互相靠近.每只蝴蝶释放出的香味Ffit计算公式如下:

式中,c为感觉因子;I为刺激强度,与蝴蝶的适应度相关;α为幂指数.
当蝴蝶感觉到另一只蝴蝶g*在这个区域散发出更多的香味时,就会去靠近,这个阶段被称为全局搜索.当蝴蝶不能感知大于它自己的香味时,它会随机移动,这个阶段称为局部搜索.设定一个概率开关b来转换全局搜索和局部搜索,公式为

式中,为第i只 蝴蝶在第t次 迭代中的空间位置;g*为 当前最优解;Ffiti为 第i只 蝴蝶的香味;和为空间中随机选择的第i只和第j只蝴蝶的位置;r和p为0到1的随机数.
1.2.2 引入Lévy flight的蝴蝶优化算法
针对蝴蝶优化算法存在容易陷入局部最优、收敛速度慢的问题,将Lévy flight引入算法.
Lévy flight由法国数学家Paul Pierre Lévy提出,是一种随机搜索策略.本文提出一种引入Lévy flight的蝴蝶优化算法(butterfly optimization algorithm with Lévy flight, LBOA),可以跳出局部最优位置,增加找到全局最优解的可能性.引入Lévy flight的搜索策略可用以下公式表示:

式中,L(ξ)表示由Lévy flight生成的随机向量;δ 为 步长因子;⊕为点对点乘法.LBOA具体步骤如下:
1)种群初始化 定义目标环境为N×D的一个空间,其中N代表种群的数量,D表示空间维度.将每个蝴蝶的位置定义为Xi=[xi1xi2xi3···xiD],i=1,2,···,N,最优位置定义为Xbest=[x1x2x3···xD].各维度搜索的上下界分别表示为BU=[bu1bu2···buD],BL=[bl1bl2···blD].通过以下公式获取初始种群位置:

2)计算适应度 定义感觉因子c,幂指数α.根据式(6)计算第i只蝴蝶的香味.
3)全局搜索 设定概率开关b,生成0到1间的随机数p.若p<b,根据式(10)进行全局搜索,否则进行第4)步局部搜索.
4)局部搜索 根据式(8)进行局部搜索.
5)更新最优位置 根据式(6)计算蝴蝶移动后的新适应度值,更新全局最优解位置Xbest.
1.2.3 数值试验与结果分析
选用6个典型基准测试函数对LBOA进行测试,分别为sphere(f1)、Schwefel 2.22(f2)、noisy quadric(f3)、Griewank(f4)、Rastrigin(f5)和Ackley(f6)函数.所有测试函数均为最小化问题,理论最优值fmin=0,维度为30.其中函数f3加入了噪声.函数的搜索范围见文献[13].
算法性能的评价标准有以下三个准则:① 平均值,反映算法的寻优能力和收敛精度;② 标准差,反映算法的稳定性;③ 成功率,算法在达到给定迭代次数情况下,进行多次独立运行后,求解成功的次数占总运行次数的百分比.
测试算法初始参数统一设置为:种群大小N为30,最大迭代次数Tmax为 1 000,维度D为30,算法测试均独立运行30次.试验测试环境为:Intel(R) Core(M) i5-4260U处理器,4 GB内存,MATLAB R2016b.表1为算法改进前后的寻优结果.

表1 BOA改进算法寻优结果Table 1 Optimization results of the improved BOA algorithm
观察表1中6个测试函数的结果,LBOA的三个评价指标均优于BOA.其中,函数f3和f5的三个指标均有改善,其他函数在均值和标准差指标上均有明显提升.可以看出LBOA在寻优能力和稳定性方面均有很大提高.同时,本文采用收敛曲线来反映算法在收敛速度方面的表现.图1为测试函数f6的收敛曲线,可以看出,LBOA具有更快的收敛速度.

图1 f6收敛曲线Fig.1 Convergence curves off6
由于Kriging模型的相关参数决定了其精度,将LBOA应用于Kriging模型的优化中,可快速且准确地寻找到最优的相关参数,提高Kriging模型的精度,从而提高模型修正的效率和精度.
2 模型修正方法
2.1 提升小波变换
传统的小波变换得到的数值为浮点数,对它们进行压缩时,需要通过量化才能得出对应的整数,此过程会产生误差[14].Sweldens提出了提升小波变换算法,该算法使用数乘运算替代了传统小波变换中的卷积运算,包含分裂、预测和更新三个过程[15],如图2所示.
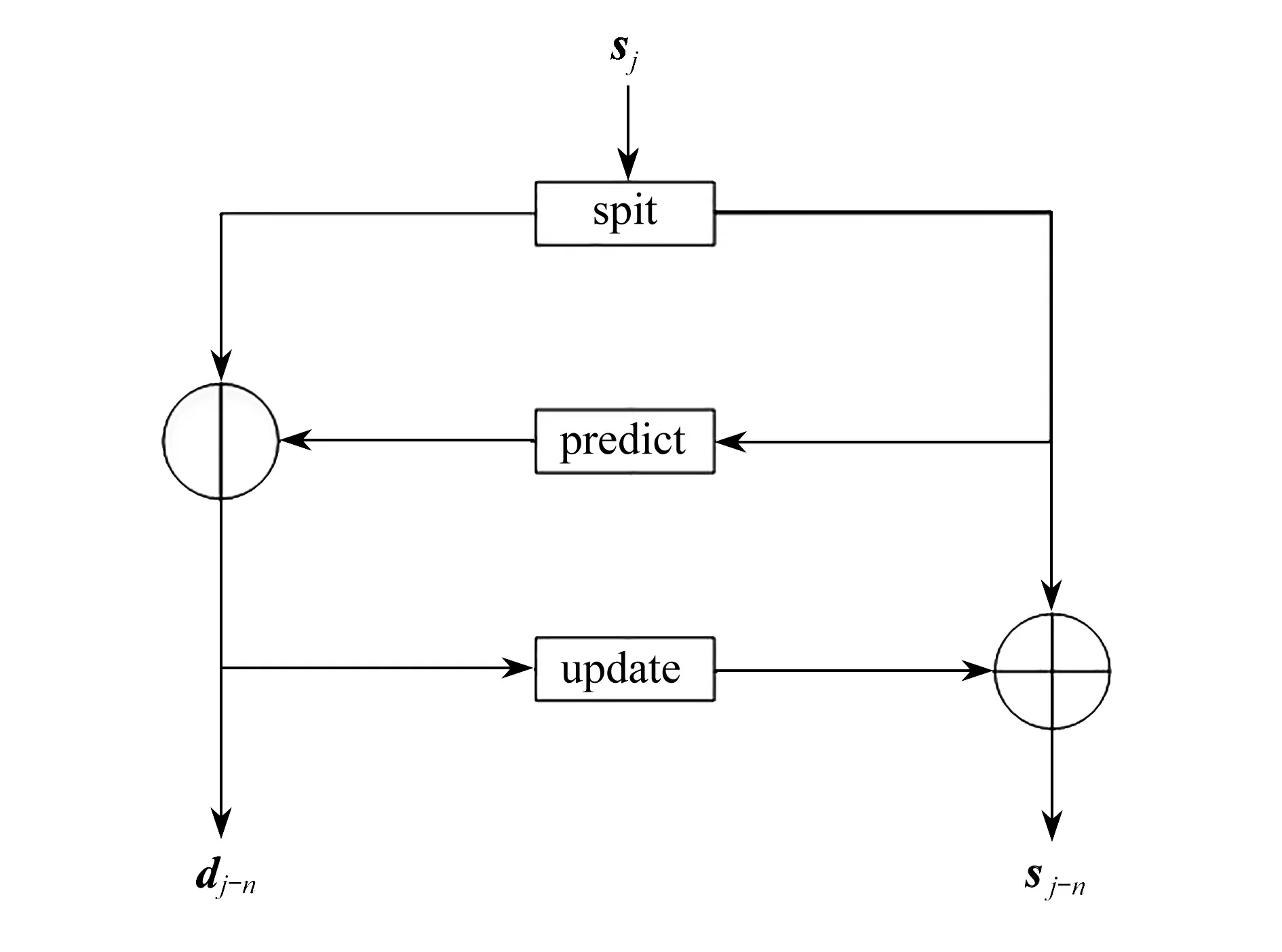
图2 提升小波变换过程Fig.2 The process of the lifting wavelet transform
原始信号sj经过提升小波变换后分解为高频分量dj-1和 低频分量sj-1;对低频分量再进行分裂、预测和更新,sj-1进 一步分解成第二层高频dj-2和 第二层低频sj-2;经过n层提升小波分解后,原始信号可表示为{sj-n,dj-n,···,dj-1}.
提升小波变换后的近似系数(低频分量)保留了与原始信号相同的特征和全局特性.因此,对AFRF进行提升小波变换后的近似系数中包含丰富的时域信息和精确的频域局部化信息[14],能够以响应特征量的形式替代AFRF进行模型修正.由于对AFRF进行变换属于离散变换,且考虑到小波基的正交性、支撑长度和消失距对变换的影响,经过多次对比试验,选取特性适中的db5小波基作为提升方案.在提升变换的过程中,若分解层数过少会使单层系数过多,导致计算量过高;反之分解层数过多会使近似系数保留的原始信息过少.两者均会影响模型修正的效果.为平衡模型修正计算速度与修正精度,使用db5小波提升方案对AFRF做5层提升小波变换,提取第5层近似系数作为AFRF的特征量构建Kriging模型,进行模型修正.提取过程如图3所示.

图3 近似系数提取流程Fig.3 The flow chart of extracting approximate coefficients
2.2 Wasserstein距离
Wasserstein距离在生成对抗网络、线性规划和拓扑分析等方面逐步得到应用,成为近年来的热门[16].在统计学方面,Wasserstein距离可应用于三个方面:① 由于其具有可以诱导拓扑且易于优化的优点,通常用于渐近理论研究;② 用于结构模型参数的统计推断和拟合优度检验;③ Wasserstein距离的概率空间可以代替样本或参数空间进行数据分析.
拟合优度检验可以对系统数据建模的拟合状态进行相似性评估[17].本文利用Wasserstein距离进行拟合优度检验,对两个概率分布之间的相似程度进行度量.Wasserstein距离的形式为

式中, Π (P,Q)为 两个概率分布P和Q组合起来的所有可能的联合分布的集合,记作γ ;E(x,y)~γ[‖x-y‖]为关于‖x-y‖的 期望,可写作∫ ‖x-y‖dγ(x,y);inf代表最大下界.
对于每一个可能的联合分布γ ,可以从 (x,y)~γ 中 抽取一对样本x和y,并计算出这对样本的距离‖x-y‖,因此可以计算在该联合分布 γ下,样本对距离的期望值.在所有可能的联合分布中,这个期望的下界即为Wasserstein距离[18].
2.3 修正流程
对待修正参数的真实数值进行偏移,模拟由不确定因素导致的模型偏差.抽取一定量待修正参数样本作为Kriging模型的输入,计算其对应的AFRF并做提升小波变换,选取第5层近似系数作为Kriging模型的响应输出,使用LBOA优化Kriging模型的相关参数,构造并检验代理模型精度.Kriging模型构造完成后,即可代替有限元模型进行响应计算.
抽取200组真实分布下的样本,分别计算AFRF并进行算术平均,模拟实测数据.对平均后的AFRF进行相同的提升小波变换,选取第5层近似系数作为实测响应.以模拟实测的AFRF提升小波变换得到的近似系数与Kriging模型预测的近似系数之间的Wasserstein距离最小作为目标函数,使用鲸鱼优化算法迭代求解即可得到修正后参数.
鲸鱼优化算法是一种新型群体智能优化算法,模拟了螺旋气泡网进食策略达到优化的目的,具有良好的全局和局部搜索机制、收敛速度快和稳定性好等优点[19].本文使用鲸鱼优化算法求解待修正参数均值,模型修正流程图如图4所示.
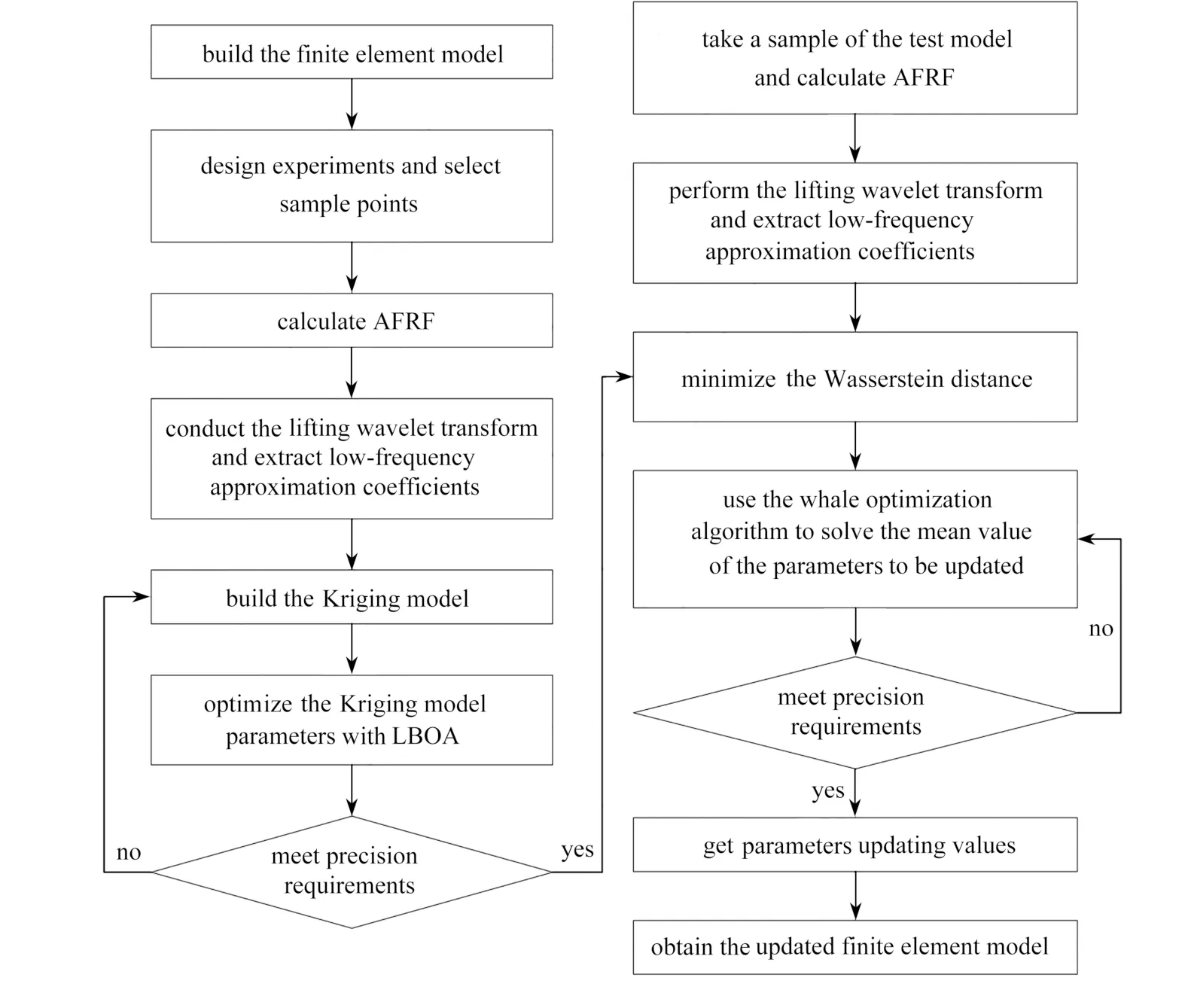
图4 模型修正流程图Fig.4 The flowchart of model updating
3 数值算例
3.1 二维桁架
二维桁架结构如图5所示,该桁架模型由36个杆单元组成,共有16个节点和29个自由度.杆件的弹性模量E=190GPa ,密度 ρ =7800kg/m3,单元横截面积为1 cm2.激励位置和测点位置分别取在节点5、13的Y方向自由度.结构在服役时刚度会降低,由于弹性模量和截面尺寸决定了刚度值,而截面尺寸一般保持不变,本算例选取灵敏度较高的杆件,对其弹性模量进行偏移作为初始有限元模型的均值.首先,对杆件的弹性模量扰动2%进行灵敏度测试,得到参数对结构AFRF的灵敏度如图6所示.

图5 二维桁架结构Fig.5 The 2D truss structure
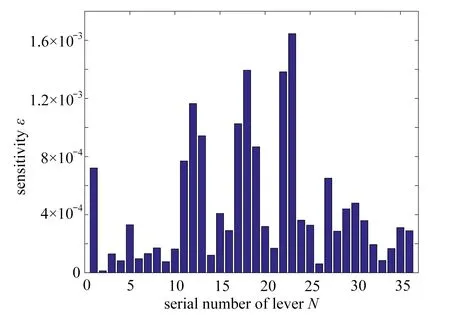
图6 参数对结构AFRF的灵敏度Fig.6 Sensitivity of structure AFRF to parameters
选取灵敏度较高的四个杆件的弹性模量E㉓,E⑱,E㉒,E⑫作为待修正参数,将E㉓和E㉒的有限元均值降低10%、E⑱和E⑫的有限元均值增加10%作为初始值.
其次,采用拉丁超立方抽样抽取200组样本,选取前150组作为训练集,后50组作为测试集,计算AFRF并做提升小波变换,选取第5层近似系数构建Kriging模型.为提高Kriging模型的精度,使用LBOA优化Kriging模型的相关参数.表2为LBOA与BOA寻优结果对比,可以看出,两种算法消耗的时间几乎一样,而LBOA的寻优结果更加接近最优值,表明LBOA具有更强的寻优能力.本文选取组数为奇数的测试样本来检验Kriging模型对第10个近似系数的预测效果,如图7所示.

表2 寻优结果对比Table 2 Comparison of optimization results

图7 Kriging模型精度评估Fig.7 Accuracy evaluation of the Kriging model
可以看出,构造的Kriging模型预测值和真实值几乎重合,RMSE值均低于3×10-9,说明构造的Kriging模型的预测精度很高,可以代替有限元模型进行模型修正.
最后,在服从以试验模型参数为均值的Gauss分布中随机抽取200个样本,计算AFRF并进行算术平均.对平均后的AFRF进行相同的提升小波变换,提取第5层近似系数作为仿真试验响应,以最小化Wasserstein距离作为目标函数,通过鲸鱼优化算法迭代求解待修正参数的均值.修正后的均值及误差如表3所示.

表3 桁架结构修正前后参数均值及误差Table 3 Parameter mean values and errors of the truss structure before and after updating
可以看出,四个参数修正后的均值的相对误差较小,均低于0.07%,达到了较高的修正精度.AFRF修正前后曲线的比较如图8所示,可以看出模型修正后的频响函数与模拟实测的频响函数的重合度较高,验证了本文方法的有效性.

图8 修正前后加速度频响函数曲线Fig.8 AFRF curves before and after updating
为进一步检验所提方法的修正效果和效率,分别使用AFRF和变换后的近似系数作为响应特征量进行模型修正,比较其在Kriging模型的构建和修正效果方面的优劣.由表4可以看出,将AFRF进行提升小波变换取近似系数作为响应指标进行模型修正,不仅提高了各个参数的修正精度,且缩短了Kriging模型构建消耗的时间,进而提高了模型修正效率.

表4 不同响应指标下的结果对比Table 4 Comparison of results under different response indicators
3.2 三维桁架
3.2.1 试验设计
三维桁架结构包括66个单元、28个节点和48个自由度,总长2.80 m、宽0.39 m、高0.27 m.桁架由4个支座固定约束(节点编号为1、8、9、16),所有节点均为铰接连接.结构的激励位置和响应位置如图9所示.
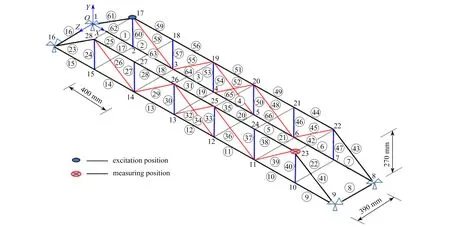
图9 三维桁架结构Fig.9 The 3D truss structure
选择结构的材料参数密度(ρ)、弹性模量(E)和尺寸参数上弦杆横截面积(A)共三个参数的均值作为待修正参数.试验有限元模型的ρ,E和A的均值分别为7 800 kg/m3、190 GPa和85.5 mm2,分别将 ρ减少10%,E增加10%,A增加10%,得到初始有限元模型的参数均值分别为7 020 kg/m3、209 GPa和95 mm2.
3.2.2 提升小波变换及系数选取
采用拉丁超立方抽样选取初始样本点,计算有限元模型AFRF,对AFRF进行提升小波变换,选取第5层近似系数.由于提升小波变换得到的近似系数既可以剔除噪声的干扰,又可提高计算速度,且保留了原始信号中的大量信息,因此可以简化并代替由大量频率点组成的频响函数.图10为提升小波变换得到的第1、3、5层近似系数.

图10 第1、3、5层近似系数Fig.10 Approximate coefficients for the 1st, 3rd and 5th levels
3.2.3 Kriging模型的构建及评估
在初始有限元值的±20%区间内,用拉丁超立方抽样得到的200个样本构造Kriging模型,其中前150个样本作为训练集输入Kriging模型,对应AFRF变换后得到的近似系数作为Kriging模型的输出,构建初始的代理模型;后50个样本作为测试集,以测试集Kriging模型的均方误差(MSE)的均值最小作为LBOA的目标函数,寻找相关参数θk的最优值.算法参数设置:种群数量N为30,维度D为1,最大迭代次数Tmax为100,参数上下界BU和BL分别为0.001和100,感觉因子c为0.3,幂指数α 为0.01.寻优得到的最优相关参数θk为0.780 6.为进一步验证LBOA的优越性,将LBOA与BOA进行对比(图11).由迭代曲线可以看出,使用LBOA时,寻优曲线更加平滑,且在10次迭代内收敛,具有较好的寻优速度.
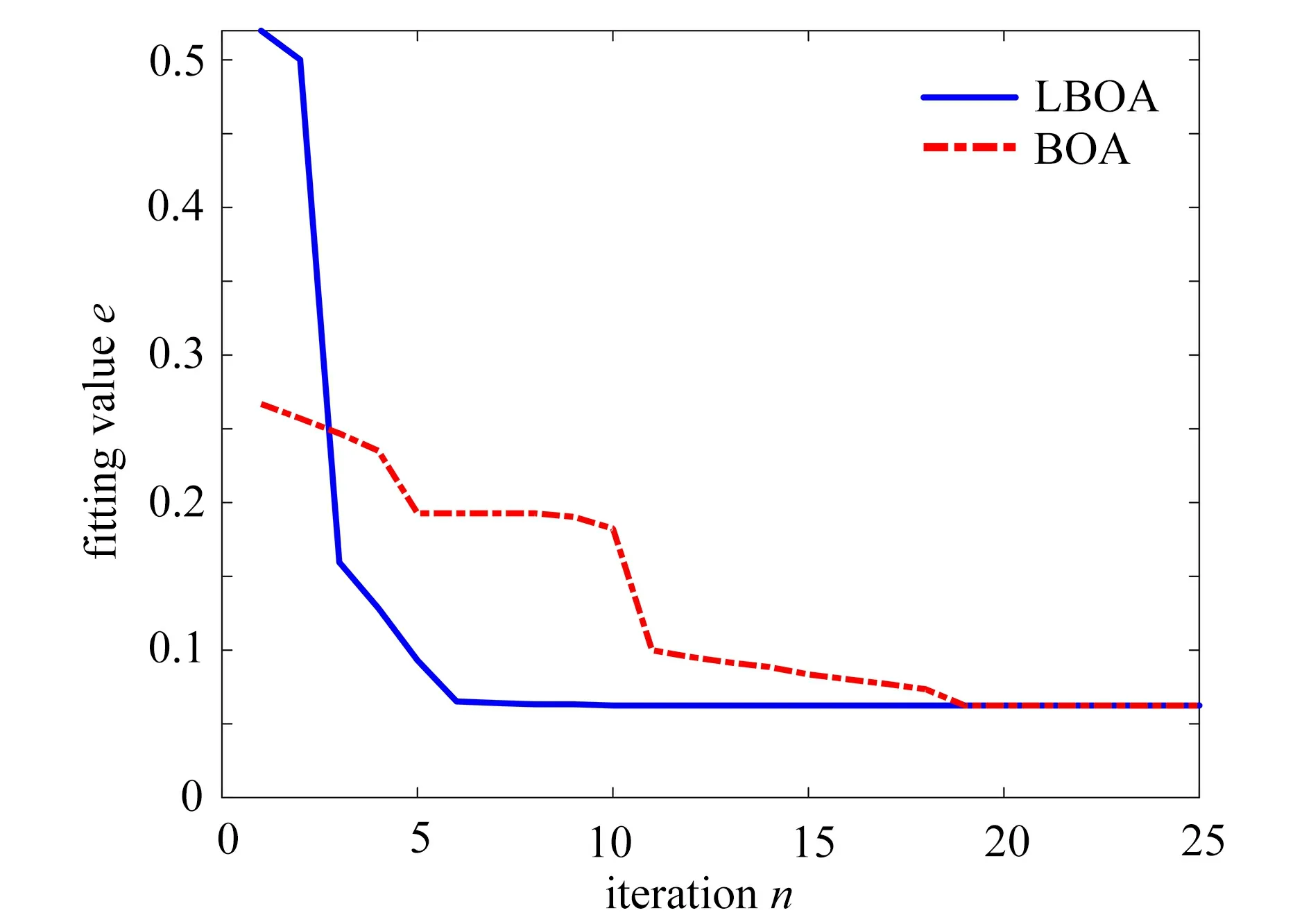
图11 Kriging模型参数寻优曲线Fig.11 Optimization curves of the Kriging model parameter
寻找到最优的 θk后即可更新Kriging模型.本文采用两种方式来评估Kriging模型的精度:测试集均方根误差(RMSE)和系数真实值与Kriging模型预测值的拟合曲线.选取组数为奇数的测试样本来检验Kriging模型对第2个近似系数的预测效果,如图12所示.

图12 Kriging模型精度评估Fig.12 Accuracy evaluation of the Kriging model
可以看出,构造的Kriging模型预测值和真实值几乎重合,RMSE值均低于1 ×10-3,说明构造的Kriging模型的预测精度较高,可以代替有限元模型进行模型修正.
3.2.4 模型修正
在服从以试验模型参数为均值的Gauss分布中随机抽取200个样本,计算AFRF并进行算术平均.对平均后的AFRF进行相同的提升小波变换,提取第5层近似系数作为仿真试验响应,以最小化Wasserstein距离作为目标函数,通过鲸鱼优化算法迭代求解待修正参数的均值.修正后的均值及误差如表5所示.

表5 桁架结构修正前后结构参数均值及误差Table 5 Parameter mean values and errors of the truss structure before and after updating
可以看出,三个参数的均值修正后的相对误差很小,均低于0.4%,表明使用本文所提方法进行随机模型修正的效果较好.将修正后的参数均值输入模型并计算AFRF,与初始模型和试验模型的AFRF作比较.图13为AFRF的实部与虚部曲线,可以看出修正后模型的曲线与试验模型的曲线基本重合,验证了所提方法的有效性.
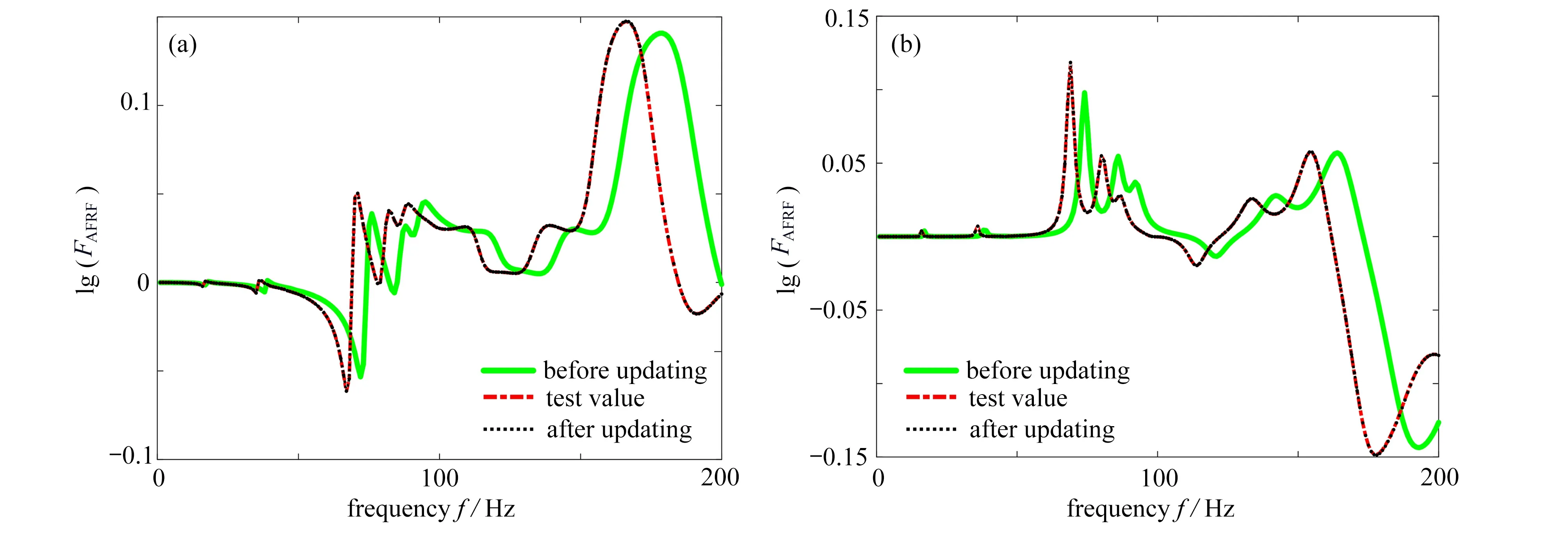
图13 修正前后加速度频响函数曲线:(a)实部曲线;(b)虚部曲线Fig.13 AFRF curves before and after updating: (a) real part curves; (b) imaginary part curves
4 结 论
1)本文将提升小波变换引入模型修正中,对加速度频响函数进行提升小波变换来选取近似系数,可以保留原始信号的特征和全局特性,将大量的结构信息集中至少量的系数中,避开了频响函数的频率点选择困难的问题,提高了修正效率.
2)为避免BOA陷入局部最优,本文将Lévy flight策略引入BOA,提高蝴蝶全局位置更新的能力.结果证明,相比于原算法,LBOA具有更好的收敛精度和寻优稳定性,且拥有更快的寻优速度.并将其应用于Kriging模型的相关参数寻优,提高了Kriging模型的精度,从而代替有限元模型进行模型修正,提高了修正效率.
3)本文利用Wasserstein距离进行拟合优度检验,衡量实测响应的近似系数与Kriging模型预测的近似系数的相似度,并结合寻优算法寻找均值,提高了随机模型修正的效率.
参考文献( References ):
[1]张皓, 李东升, 李宏男.有限元模型修正研究进展: 从线性到非线性[J].力学进展, 2019, 49: 542-575.(ZHANG Hao,LI Dongsheng, LI Hongnan.Recent progress on finite element model updating: from linearity to nonlinearity[J].Advances in Mechanics, 2019, 49: 542-575.(in Chinese))
[2]STEENACKERS G, GUILLAUME P.Finite element model updating taking into account the uncertainty on the modal parameters estimates[J].Journal of Sound and Vibration, 2006, 296(4/5): 919-934.
[3]TSHILIDZI M.Finite-Element-Model Updating Using Computional Intelligence Techniques[M].London: Springer, 2010.
[4]方圣恩, 林友勤, 夏樟华.考虑结构参数不确定性的随机模型修正方法[J].振动、测试与诊断, 2014, 34(5): 832-837,973.(FANG Sheng’en, LIN Youqin, XIA Zhanghua.Stochastic model updating method considering the uncertainties of structural parameters[J].Journal of Vibration,Measurement and Diagnosis, 2014, 34(5): 832-837,973.(in Chinese))
[5]DENG Z M, BI S F, SEZ A.Stochastic model updating using distance discrimination analysis[J].Chinese Journal of Aeronautics, 2014, 27(5): 1188-1198.
[6]万华平, 任伟新, 黄天立.基于贝叶斯推理的随机模型修正方法[J].中国公路学报, 2016, 29(4): 67-76, 95.(WAN Huaping, REN Weixin, HUANG Tianli.Stochastic model updating approach by using Bayesian inference[J].China Journal of Highway and Transport, 2016, 29(4): 67-76, 95.(in Chinese))
[7]ZHAI X, FEI C W, CHOY Y S, et al.A stochastic model updating strategy-based improved response surface model and advanced Monte Carlo simulation[J].Mechanical Systems and Signal Processing, 2017, 82: 323-338.
[8]陈喆, 何欢, 陈国平, 等.考虑不确定性因素的有限元模型修正方法研究[J].振动工程学报, 2017, 30(6): 921-928.(CHEN Zhe, HE Huan, CHEN Guoping, et al.The research of finite element model updating method considering the uncertainty[J].Journal of Vibration Engineering, 2017, 30(6): 921-928.(in Chinese))
[9]JALALI H, KHODAPARAST H H, MADINEI H, et al.Stochastic modelling and updating of a joint contact interface[J].Mechanical Systems and Signal Processing, 2019, 129: 645-658.
[10]ZHAO Y L, DENG Z M, ZHANG X J.A robust stochastic model updating method with resampling processing[J].Mechanical Systems and Signal Processing, 2020, 136: 106494.
[11]邓振鸿, 张保强, 苏国强, 等.基于近似似然的频响函数不确定性模型修正[J].振动、测试与诊断, 2020, 40(3): 548-554, 628.(DENG Zhenhong, ZHANG Baoqiang, SU Guoqiang, et al.Uncertainty model updating of frequency response function based on approximate likelihood function[J].Journal of Vibration,Measurement and Diagnosis,2020, 40(3): 548-554, 628.(in Chinese))
[12]韩忠华.Kriging模型及代理优化算法研究进展[J].航空学报, 2016, 37(11): 3197-3225.(HAN Zhonghua.Kriging surrogate model and its application to design optimization: a review of recent progress[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225.(in Chinese))
[13]ARORA S, SINGH S.Butterfly optimization algorithm: a novel approach for global optimization[J].Soft Computing, 2018, 23(3): 715-734.
[14]宋国明, 王厚军, 刘红, 等.基于提升小波变换和SVM的模拟电路故障诊断[J].电子测量与仪器学报, 2010, 24(1):17-22.(SONG Guoming, WANG Houjun, LIU Hong, et al.Analog circuit fault diagnosis using lifting wavelet transform and SVM[J].Journal of Electronic Measurement and Instrument, 2010, 24(1): 17-22.(in Chinese))
[15]SWELDENS W.The lifting scheme: a construction of second generation wavelets[J].SIAM Journal on Mathematical Analysis, 1998, 29(2): 511-546.
[16]PANARETOS V M, YOAV ZEMEL Y.Statistical aspects of Wasserstein distances[J].Annual Review of Statistics and Its Application, 2019, 6(1): 405-431.
[17]周平, 赵向志.面向建模误差PDF形状与趋势拟合优度的动态过程优化建模[J].自动化学报, 2021, 47(10): 2402-2411.(ZHOU Ping, ZHAO Xiangzhi.Optimized modeling of dynamic process oriented towards modeling error PDF shape and goodness of fit[J].Acta Automatica Sinica, 2021, 47(10): 2402-2411.(in Chinese))
[18]肖先勇, 桂良宇, 李成鑫, 等.基于Wasserstein距离的多电压暂降事件同源检测方法[J].电网技术, 2020, 44(12):4684-4693.(XIAO Xianyong, GUI Liangyu, LI Chengxin, et al.Multiple voltage sag events homology detection based on Wasserstein distance[J].Power System Technology, 2020, 44(12): 4684-4693.(in Chinese))
[19]SEYEDALI M, ANDREW L.The whale optimization algorithm[J].Advances in Engineering Software, 2016,95(5): 51-67.

