含多个矩形加热器通道内流动沸腾传热性能的介观数值方法研究*

李迎雪， 王浩原， 娄 钦

（1.上海理工大学 能源与动力工程学院，上海 200093；2.上海理工大学 上海市动力工程多相流动与传热重点实验室，上海 200093）

引 言

随着现代科技的发展，设备的散热问题愈发受到关注，例如核反应堆冷却和芯片散热等[1-3].沸腾作为一种有效的散热方式，在较低温度下即可实现较高的传热效率，因此得到了广泛的应用.沸腾可以分为池沸腾和流动沸腾两种，和池沸腾相比，流动沸腾中常伴随着更剧烈的对流传热及相变速率，从而可以达到更高的换热效率，因此流动沸腾受到了越来越多的关注[4].

在流动沸腾中，热源对相变过程及传热效率有着至关重要的影响[5-7]，因此许多研究者研究了不同加热器对流动沸腾的影响.例如，Gong和Cheng[8]在水平管道内放置一微型加热器，研究了不同入口速度、接触角和加热器尺寸对饱和流动沸腾的影响，他们发现随着入口速度的增加或加热器长度的减小，流型从环状流变为段塞流，并且在段塞流阶段，通道中的气泡段塞长度减小.Tan等[9]研究了水平管内壁面润湿性对流动沸腾性能的影响，比较了亲水性表面、疏水性表面和梯度润湿性三种情况，研究发现梯度润湿性可以结合接触角的连续变化效应以及亲水和疏水表面的优点，限制段塞流的出现，使通道内更多的区域表现为气泡流状态.Yin等[10]使用流体体积模型和气液相变模型模拟了分离型热管蒸发器中垂直管内的流动沸腾，研究了低热流密度下管道内不同高度的气泡形态变化，发现沸腾的流动模式随管的高度而变化.可以看出，加热器垂直或水平的放置方式对流动沸腾中气泡运动和壁面换热有着明显的影响.因此，Azizifar等[11]通过实验研究了水的过冷流动沸腾过程，结果表明，与普通管相比，金属泡沫导致沸腾传热系数（heat transfer coefficient，HTC）显著增加，金属泡沫管放置方式不同时，水平放置的传热效率比垂直放置高10%.

上述流动沸腾的研究中均采用了单个加热器加热方式，最近有研究指出[12]，多个加热器加热时，会产生多个气泡成核位点，气泡间的相互作用会导致部分成核位点失活从而降低传热效率.因此，多个加热器引起的流动沸腾逐渐受到关注.Vontas等[13]模拟了多个成核位点和同一成核位置发生多次重复成核的情况,观察到表面润湿性对换热系数具有显著影响，发现亲水和疏水表面的主要传热机制分别是液膜蒸发和接触线蒸发.Sun等[14]研究了由多个加热器引起的流动沸腾，通过气泡成核、生长、离开、聚结的行为，讨论了单相流、气泡流、段塞流和核态沸腾转折点（departure from nucleate boiling， DNB）多种流动模式的行为.同时研究了热通量、Reynolds数、流动通道宽度、成核点宽度等因素对流动沸腾的影响，特别是对DNB点的影响.Yadav等[15]对多个加热器引起的流动沸腾进行了空隙率的局部测量，观察到低入口过冷度比高入口过冷度时的局部空隙率更高.此外，改变加热器的位置可以改变观察孔隙率的径向位置，增加加热器的数量可以增加孔隙率.但是，他们工作中并没有考虑多个加热器之间的相互影响.Baltis等[16]研究了垂直排列的加热器之间的相互影响，发现上游的加热器通过额外对流可以增加下游加热器的气泡成核频率和气泡脱离直径，随着加热器间距的增加，这种促进作用越来越小.此外，上游加热器产生的成核气泡会抑制下游的气泡成核，这种抑制趋势的影响随着下游气泡成核频率的增加而减弱.从上述研究可以看出，关于多加热器引起的流动沸腾研究还存在一些不足，不同加热器表面气泡去除的动力学行为差异和不同加热器表面的传热性能差异尚不明确，例如，当加热器的长度不同或相邻两个加热器之间距离不同的情况下，气泡动力学行为差异和加热器表面的热流密度差异.

格子Boltzmann方法（lattice Boltzmann method, LBM）是20世纪80年代中期建立和发展起来的一种模拟方法，它是介于流体的微观分子动力学模型和宏观连续模型之间的介观数值模型，它兼具二者的优点，可以直观、方便地描述流体与周围环境之间的相互作用.近年来该方法经常被用于研究渗流、多相流、微流体等流动问题[17-19].因此，本文基于格子Boltzmann方法模拟了通道内多加热器下的流动沸腾，详细研究了不同矩形加热器（包括矩形加热器的间距、矩形加热器的尺寸及其表面润湿性的不同）对气泡动力学行为和传热性能的影响.

1 数值方法

1.1 伪势LB两相流模型

本文采用Gong和Cheng提出的改进伪势LB两相流模型来模拟通道中的流动沸腾[4].模型包含两个粒子分布函数的演化方程，一个是密度分布函数，另一个是温度分布函数.接下来，给出了伪势LB两相流模型的简要描述.

密度分布函数的演化方程如下：

其中gs代 表流固之间的相互作用力强度；s(x)是一个开关系数，当格点x为流体点时，其值为0，此时对应的Fads为 0，即表示不存在流体与固体间的相互作用力；当格点x为固体点时，s(x)的值为1.

其他外部作用力Fext的表达式为

其中g表示重力加速度，ρave是单个时间步长整个计算区域内流体的平均密度.

流体密度ρ和速度U的表达式为

在本文工作中，采用二维九速（D2Q9）数值模型进行研究.在D2Q9模型中对应的权重系数为 ω0=4/9；ωi=1/9 ，i=1, 2, 3, 4；ωi=1/36，i=5, 6, 7, 8.其离散速度模型为

1.2 能量方程

和密度分布函数类似，本文的温度场由温度分布函数得到，其演化方程如下：

其中gi(x,t)表示粒子在x位置t时刻i方 向的温度分布函数； τT是 温度的无量纲松弛时间，它的值与热扩散率α有关，为平衡态温度分布函数，其具体表达式为

式（12）中的ϕ 代表的是源项，可以表示为

此处的T是宏观温度，可以通过温度分布函数得到：

2 模型与验证

2.1 计算模型

本文采用相变LB模型研究通道内的流动沸腾.所研究物理问题的示意图如图1所示，通道长和宽分别为Lx=10 mm和Ly=3 mm，在通道的底部分布着若干个长和高分别是L和H的矩形加热器，加热器之间的距离为D，加热器个数记为N，加热器表面接触角为θ.初始时通道内充满了密度为ρl=5.426，温度为Tsat=0.9Tc的饱和水，在计算域内部沿x方向对流体施加一个水平惯性力Fx，y方向上浮力为Fy=Fext.加热器底部为恒温边界条件[21]，加热器左右两侧绝热，底部其他区域和计算域顶部均为无滑移绝热边界.计算域左右两边均采用周期性的边界条件，本文中浮力与惯性力的关系为Fx=0.9Fy，重力加速度设置为g=（0,g），g=8 × 10-5.其他一些参数在模拟中固定如下：a=2/49，b=2/21，R=1.0，cv=6.0，ρl=5.426，ρg=0.811 3，加热器的高度固定为H=2.另外，如无特别指明，本文中所有单位均为格子单位.

图1 计算域示意图Fig.1 The computation domain

2.2 模型验证

为了验证模型的正确性，我们计算了沸腾过程中不同重力加速度值下的单气泡脱离直径d.在初始时刻，计算域内充满了Tsat=0.9Tc的饱和水，并且在底壁的中心放置一个L×H的高温加热器.加热器底部为恒温边界条件[21]，加热器左右两侧绝热.计算域底部其他区域和计算域顶部均为无滑移绝热边界，左右边界都为周期性的边界条件.对于该模型验证中，气泡脱离直径d与重力加速度相关[22]：

为了验证这种关系，在不同的重力加速度值下进行了模拟，即模拟中g=2 × 10-5，4 × 10-5， 6 × 10-5， 8 ×10-5， 1 × 10-4，计算域为Lx×Ly=400 × 200.得到的气泡脱离直径见图2，其中方形点表示气泡离开的直径，曲线为拟合结果.图2中拟合曲线的指数为-0.507 3，与实验预测的-0.5吻合良好.

在进行数值模拟之前，首先进行网格无关性验证.表1给出了网格大小分别为Lx×Ly=500 × 150，Lx×Ly=1 000 × 300，Lx×Ly=2 000 × 600三种情况下流动沸腾过程中加热器表面的空间-时间平均热流密度Qave.其中加热器表面接触角θ=90°，其他参数设置和2.1小节相同.从表1中可以看出，网格数为Lx×Ly=500 × 150时的平均热流密度低于其他两种情况，此外，网格大小Lx×Ly=1 000 × 300和Lx×Ly=2 000 × 600两种情况下的平均热流密度变化相对误差为4.054%.因此，考虑到计算效率和计算精度，本文网格大小选取为Lx×Ly=1 000 ×300，对应的dy=0.01 mm，即最小壁面法向网格尺度为0.01 mm.

表1 网格无关性Table 1 Grid independence

3 数值结果与分析

3.1 加热器间距的影响

本小节研究加热器间距对流动沸腾的影响，这里主要考虑了加热器间距D=1 000，500，333，250四种情况下的流动沸腾，模拟中加热器长度L=22，每个加热器的表面接触角均为90°.

图3所示为中性表面情况下加热器间距D=1 000时气泡从生长到离开的过程.如图所示，气泡在t=4 000时成核，此时气泡形状为一个半椭圆形，随着沸腾过程的进行，在t=10 000～21 000时刻可以很明显看出气泡由于惯性力作用向下游偏离.在t=10 000，15 000，17 000时刻，随着时间的推移，气泡在浮力和惯性力下和加热器的接触长度越来越小，同时气泡面积越来越大，最终气泡在t=19 000时刻脱离加热器表面.随后在t=21 000时刻，加热器表面产生成核气泡，代表第二个沸腾循环的开始.

图3 D=1 000时计算域的密度分布Fig.3 Density distributions for D=1 000

图4为加热器间距D=500，333，250时的气泡演化过程.如图所示，与图3中的气泡成核时间相同，D=500，333，250时得到的气泡成核时间也是t=4 000时刻，表明加热器间距不影响气泡成核时间.然而不同的加热器间距对气泡脱离加热器表面的时间有很大影响.当D=500时，气泡脱离时间在t=21 000时刻；当D=333时，气泡脱离时间在t=24 000时刻；当D=250时，气泡在t=29 000时刻脱离加热器表面，即加热器间距越小，气泡越难以脱离加热器表面，且气泡的生长周期越长.这是因为加热器间距较短时在加热器表面产生的气泡之间的相互作用力越大，该相互作用力影响周围的流体运动和传热.

图4 不同加热器间距时计算域的密度分布：（a）D=500；（b）D=333；（c）D=250Fig.4 Density distributions with different heater spacings: (a)D=500; (b) D=333; (c) D=250

从图4还可以看出不同加热器间距下得到的气泡大小也不相同，为了详细说明这一现象，图5给出了不同加热器间距下气泡脱离前其面积A随时间的变化，这里的气泡面积为计算域内密度小于 0 .5×(ρl+ρg)的流体格点所占的区域.需要说明的是，由于本文主要研究加热器对流动沸腾的影响，因此这里主要统计气泡脱离壁面之前的面积，而气泡脱离加热器之后面积变化受很多因素，例如流体温度、惯性力大小等的影响，这里暂不讨论.从图中可以看出，对于不同的加热器间距，气泡面积几乎从同一时刻开始增加，这和图4所示的不同加热器间距得到的气泡成核时间相同的结论一致.从图5可以看出，在气泡成核之后，四种不同加热器间距的气泡面积都随时间的推移而增加，气泡脱离时加热器间距越大气泡面积越大，Wang等同样也发现了加热器间距对气泡面积的大小有影响[12].由于较大的气泡面积可以导致较大的浮力和惯性力，所以，加热器间距越大，气泡脱离时间越早.通常情况下，较大的气泡可以从加热器表面带走更多的热量.

图5 不同加热器间距下的气泡面积变化Fig.5 The bubble areas with different heater spacings

为了进一步说明加热器间距对流动沸腾的影响，图6给出了不同加热器间距下加热器表面平均热流密度随时间的变化，其中图6（a）给出了加热器表面空间平均热流密度随时间的变化，图6（b）给出了加热器表面空间-时间平均热流密度.从图6（a）中可以看出，气泡成核之后，间距越大的加热器表面空间平均热流密度Q越大.图中Q值下降到最低点的时刻对应气泡脱离时刻，分别对应图3中t=19 000时刻，图4（a）中t=21 000时刻，图4（b）中t=24 000时刻和图4（c）中t=29 000时刻.可以看出，在相同的时间内，沸腾周期随着加热器间距的增大而减小.图6（b）为t=0～60 000时间内加热器表面的空间-时间平均热流密度Qave，不难发现，随着加热器间距的增加，加热器表面的空间-时间平均热流密度值变大.当加热器间距从250增加到1 000时，其传热性能可以提高约12%.

图6 不同加热器间距下加热器表面平均热流密度的变化：（a）加热器表面空间平均热流密度随时间的变化；（b）加热器表面空间-时间平均热流密度Fig.6 Heat fluxes on the heater surface with different heater spacings: (a) temporal variations of the spatial average heat flux on the heater surface;(b) the temporal and spatial average heat flux on the heater surface

3.2 加热器长度的影响

本小节研究了加热器长度对流动沸腾过程中气泡面积和表面平均热流密度的影响.模拟中，计算域底部相邻两个加热器中心的距离D=500，每个加热器的表面接触角均为90°.分别考虑加热器的长度L=16，18，20，22四种情况.

图7所示为4种不同加热器长度的气泡演化过程.如图所示，以加热器长度L=16的情况为例，在t=12 000时刻加热器表面产生成核气泡，随着沸腾过程进行，气泡面积逐渐变大，其受到的浮力和惯性力也随着变大，在t=32 000时刻，气泡在浮力和惯性力作用下向右上滑移，即气泡与加热器的接触长度逐渐减小，最终气泡在t=38 000时刻完全脱离加热器，随后在t=45 000时刻第二个成核气泡产生.观察不同加热器长度下的四组气泡演化过程发现，气泡的成核时间随着加热器长度的增加而提前，这是因为随着加热器长度的增加，更多的饱和液体被加热，缩短了气泡的成核时间.另一方面，越长的加热器气泡脱离时间越早，这是因为加热器越长，表面的气泡越大，意味着加热器长度影响气泡脱离时间和气泡生长周期.

图7 不同加热器长度时计算域的密度分布：（a）L=16；（b）L=18；（c）L=20；（d）L=22Fig.7 Density distributions with different heater lengths: (a) L=16; (b) L=18; (c) L=20; (d) L=22

为进一步研究加热器长度对气泡脱离时间和气泡生长速度的影响，图8给出了不同加热器长度下，气泡脱离加热器前其面积A随时间的变化.如图所示，加热器长度越长气泡面积开始增加的时刻越靠前，虽然在不同加热器长度下，气泡面积都随时间而增加，但是气泡面积的增大速度却有所不同，在气泡成核后的10 000时长内，气泡面积增加的大小分别为401（L=22），332（L=20），257（L=18）和167（L=16）.显然，当L=22时气泡面积增加的速度最快，L=20和L=18时气泡面积增加的速度依次变慢，L=16时，气泡面积增加速度最慢.图中的最高点表示气泡脱离加热器表面时的气泡面积，可以看出，加热器越长,气泡脱离时的面积越大且脱离时间越早.上述结果表明，在加热器间距一定的情况下，加热器越长越有利于气泡生长.

图8 不同加热器长度下的气泡面积变化Fig.8 The bubble areas with different heater lengths

图9所示为不同加热器长度下加热器表面空间平均热流密度以及空间-时间平均热流密度的变化.从图9（a）可以看出，当加热器长度不同时，其表面的空间平均热流密度Q都是先降低.对于L=22，在t=4 000时刻产生成核气泡，随着气泡的生长，加热器表面的热流密度逐渐上升至最高点（t=16 000），在此之后，因为气泡与加热器的接触面积逐渐减小，热流密度Q逐渐下降，这种下降趋势在气泡与加热器表面脱离时停止（t=21 000）.不同加热器长度下的热流密度变化趋势相同，只是在时间上有一些差别.比较不同加热器长度下的热流密度曲线发现，气泡脱离加热器的时间随着加热器长度的增加而提前.这是由于加热器长度较大时，产生的气泡面积较大，其较大的浮力和惯性力促进了气泡从加热器表面的脱离.图9（b）给出了不同加热器长度下加热器表面在前80 000时刻内的空间-时间平均热流密度Qave，如图所示，加热器越长，Qave值越大，表面换热性能越好，当加热器长度从16增加到22时，其传热性能提高了13% .

图9 不同加热器长度下加热器表面平均热流密度的变化：（a）加热器表面空间平均热流密度随时间的变化；（b）加热器表面空间-时间平均热流密度Fig.9 Heat fluxes on the heater surface with different heater lengths: (a) temporal variations of the spatial average heat flux on the heater surface;(b) the temporal and spatial average heat flux on the heater surface

3.3 润湿性的影响

在沸腾过程中，受热表面的润湿性也对传热性能有显著影响.为了测试润湿性对流动沸腾的影响，本小节模拟了亲水性表面和疏水性表面两种不同情况.对于每种情况，加热器间距设置为D=500，加热器长度设置为L=22.

图10所示为亲水性表面下（θ=77°）流动沸腾过程的气泡演化.气泡在t=7 000时刻成核，t=16 000时刻后，气泡在浮力和惯性力作用下与加热器表面的接触长度越来越小，最终在t=21 000时刻脱离加热器，下一个气泡的成核时间在t=36 000时刻.图11是一个疏水性表面（θ=120°）的气泡演化过程，与亲水表面相比，气泡在疏水表面成核时间（t=2 000时刻）更早.另外，在t=26 000时刻，气泡从疏水表面脱离后疏水表面有残余气泡，这是因为疏水面对气泡的吸附力较大，这些残余气泡会作为下一个气泡的核继续生长[23-24].

图10 亲水性表面（θ=77°）时计算域的密度分布Fig.10 Density distributions on the hydrophilic surface（θ=77°）

图11 疏水性表面（θ=120°）时计算域的密度分布Fig.11 Density distributions on the hydrophobic surface（θ=120°）

不同润湿性下加热器表面平均热流密度的变化如图12所示.可以看出，在气泡成核初期（t=2 000 ～ 5 000），疏水性表面存在热流密度下降期，这是因为疏水表面上气泡成核速率更快，由于加热器尺寸的限制，较快的成核速率导致加热器表面上形成一层来不及脱离的较厚气泡，从而影响了加热区域向外的热量传递，导致热流密度降低.在t=5 000时刻，惯性力的作用表现明显，气泡发生偏离，开始向下游运动，热流密度在此时开始上升，在t=21 000时刻达到最大值，对应图11中t=21 000时刻，随后热流密度下降，t=26 000时热流密度下降到最小，在这个时刻气泡脱离，因为此时加热器表面仍然存在气泡，所以表面平均热流密度Q的值仍然较大.但是对于亲水性表面，加热器表面容易被冷的饱和液体润湿，气泡脱离之后加热器表面没有残余气泡，热流密度值明显低于疏水性表面.同时，亲水性表面气泡脱离之后加热器表面热流密度在t=20 000 ～ 30 000时刻变化缓慢，因为此时加热器表面被冷液体润湿，没有相变过程产生.比较两种润湿性下的平均热流密度，疏水性表面的平均热流密度比亲水性高26%.

图12 不同润湿性表面下加热器表面平均热流密度随时间的变化Fig.12 Temporal variations of the spatial average heat flux on the heater surface with different wettabilities

当加热器表面的润湿性不同时，流动沸腾过程中产生的气泡面积也存在差别，图13所示为不同润湿性表面下气泡面积的变化.很明显，亲水表面的成核时间晚于疏水表面，这与池沸腾的结果相同[25].对于气泡面积大小而言，亲水性表面产生的气泡面积小于疏水性表面产生的气泡面积.所以疏水性表面可以从加热器表面带走更多的热量，优于亲水性表面的传热性能.

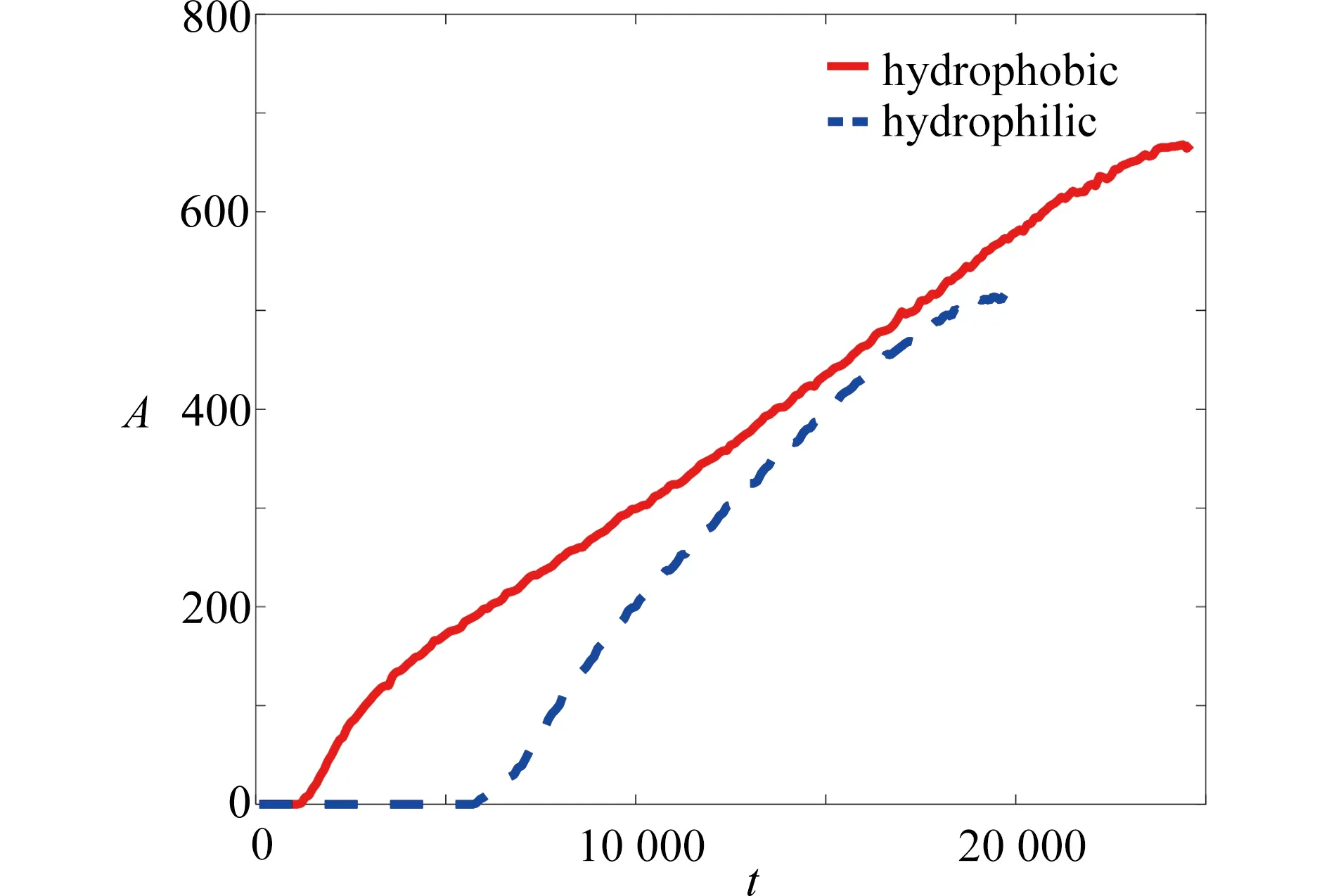
图13 不同润湿性表面下气泡面积的变化Fig.13 The bubble areas with different surface wettabilities

3.4 加热器间距、长度及润湿性的综合影响

前文中已经研究了加热器的间距、长度及润湿性对流动沸腾的影响，本节将利用正交试验方案对这三种因素进行综合考虑， 表2给出了一个三水平三因素的正交试验表及其数据分析.表2的A行中三个值分别对应的是各种因素下①水平试验指标的平均值，即（8.463 × 10-3+ 1.043 × 10-2+ 1.264 × 10-2）/3=1.051 × 10-2；（8.463 × 10-3+ 1.032 × 10-2+ 1.327 × 10-2）/3=1.069 × 10-2；（8.463 × 10-3+ 9.856 × 10-3+ 9.087 × 10-3）/3=9.135 ×10-3.同理，B、C行中三个值分别对应的是各种因素下②水平和③水平试验指标的平均值.R行中三个值为各种因素下3个水平的极差值.

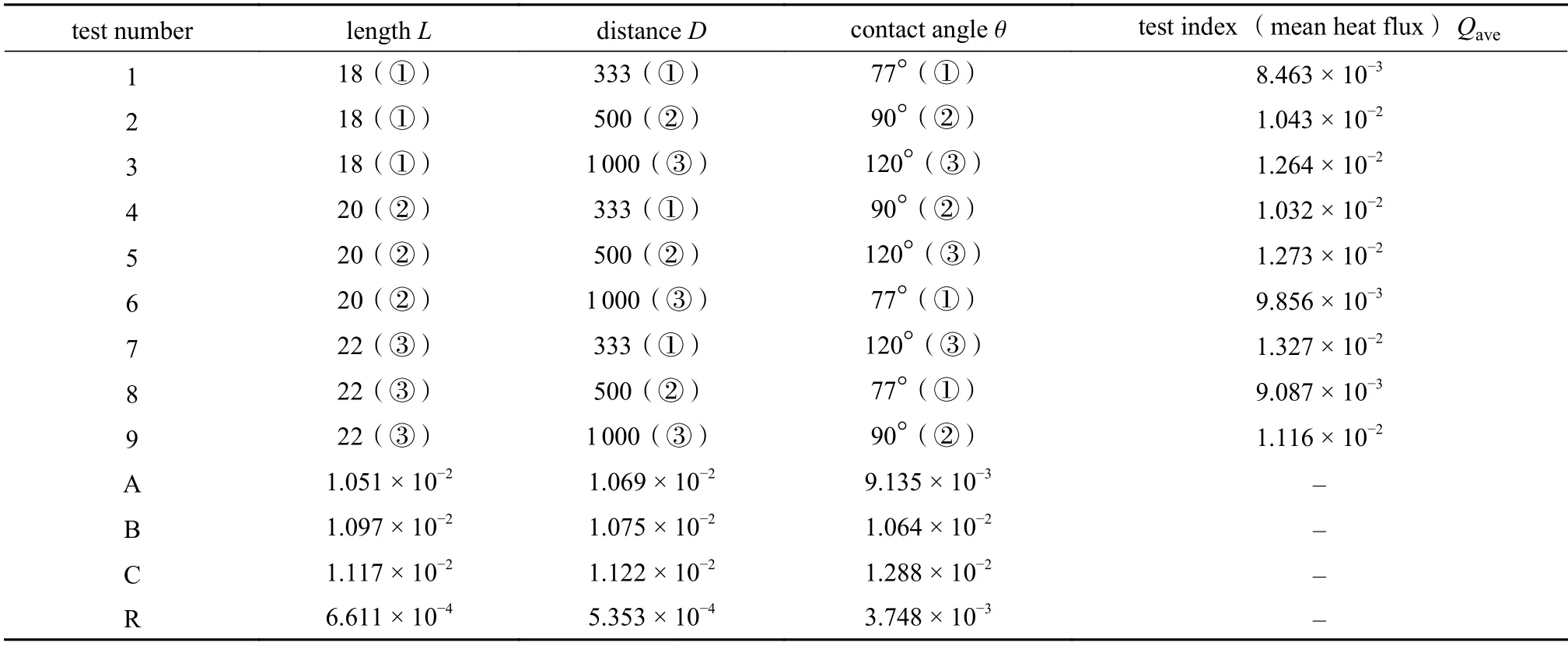
表2 正交试验表及数据分析Table 2 The orthogonal test table and data analysis

从表2可以看出，对于三种因素，都是③水平的情况下Qave值最大，①水平的情况下Qave值最小，因此可以得出结论，当加热器长度L=22，加热器间距D=1 000，加热器表面接触角θ=120°时，加热器表面的热流密度最高.另一方面，通过观察R行的值发现，接触角对Qave的影响最大，加热器长度次之，加热器间距对Qave的影响最小.

4 结 论

利用伪势LB两相流模型，模拟了含多个矩形加热器通道内流动沸腾过程中气泡成核、生长到脱离的过程.详细分析了加热器之间的距离、加热器的长度和加热器表面的润湿性对通道内流动沸腾过程中气泡动力学行为和传热的影响.结论总结如下：

1）不同加热器间距影响气泡的脱离时间和生长速率，加热器间距越大，气泡脱离时间越短，生长速率越快，加热器间距从250增加到1 000时其传热性能可以提高12%.

2）气泡成核时间随着加热器长度的增加而提前，增加加热器长度，更多的饱和液体被加热，成核气泡的生长速度加快，使气泡脱离加热器表面的时间提前.当加热器长度从16增加到22时，其传热性能提高了13%.

3）亲水性表面的气泡成核时间晚于疏水性表面的气泡成核时间，与亲水性表面相比，疏水性表面在气泡脱离加热器之后存在残余气泡.亲水性表面的平均热流密度和产生的气泡面积小于疏水性表面.加热器表面接触角从77°变化到120°，其传热性能提高了26%.

4）通过正交试验方案发现，矩形加热器表面的润湿性对流动沸腾的传热性能影响最大，加热器长度的影响次之，加热器间距的影响最小.

参考文献（ References ）：

［1］KANG M.Effect of surface roughness on pool boiling heat transfer[J].International Journal of Heat and Mass Transfer, 2000, 43（22）: 4073-4085.

［2］GOEL P, NAYAK A K, KULKARNI P P, et al.Experimental study on bubble departure characteristics in subcooled nucleate pool boiling[J].International Journal of Multiphase Flow, 2017, 89: 163-176.

［3］HE H, LIU Y, LIU L, et al.Numerical simulation of bubble growth on and departure from the heated surface by an improved lattice Boltzmann model[J].Kerntechnik, 2018, 83: 186-192.

［4］GONG S, CHENG P.A lattice Boltzmann method for simulation of liquid-vapor phase-change heat transfer[J].International Journal of Heat and Mass Transfer, 2012, 55（17/18）: 4923-4927.

［5］WANG H, LOU Q, LI L.Mesoscale simulations of saturated flow boiling heat transfer in a horizontal microchannel[J].Numerical Heat Transfer(Part A):Applications, 2020, 78（4）: 107-124.

［6］DONG Z, XU J, JIANG F, et al.Numerical study of vapor bubble effect on flow and heat transfer in microchannel[J].International Journal of Thermal Sciences, 2012, 54: 22-32.

［7］NIE D, GUAN G.Study on boiling heat transfer in a shear flow through the lattice Boltzmann method[J].Physics of Fluids, 2012, 33: 043314.

［8］GONG S, CHENG P.Numerical investigation of saturated flow boiling in microchannels by the lattice Boltzmann method[J].Numerical Heat Transfer(Part A):Applications, 2014, 65: 644-661.

［9］TAN K, HU Y, HE Y.Effect of wettability on flow boiling heat transfer in a microtube[J].Case Studies in Thermal Engineering, 2021, 26: 101018.

［10］YIN X, TIAN Y, ZHOU D, et al.Numerical study of flow boiling in an intermediate-scale vertical tube under low heat flux[J].Applied Thermal Engineering, 2019, 153: 739-747.

［11］AZIZIFAR S, AMERI M, IMAN B.An experimental study of subcooled flow boiling of water in the horizontal and vertical direction of a metal-foam tube[J].Thermal Science and Engineering Progress, 2020, 20（1）: 100748.

［12］WANG J, CHENG Y, LI X B, et al.Experimental and LBM simulation study on the effect of bubbles merging on flow boiling[J].International Journal of Heat and Mass Transfer, 2019, 132: 1053-1061.

［13］VONTAS K, ANDREDAKI M, GEORGOULAS A, et al.The effect of surface wettability on flow boiling characteristics within microchannels[J].International Journal of Heat and Mass Transfer, 2021, 172: 121133.

［14］SUN T, GUI N, YANG X, et al.Numerical study of patterns and influencing factors on flow boiling in vertical tubes by thermal LBM simulation[J].International Communications in Heat and Mass Transfer, 2017, 86: 32-41.

［15］YADAV A, ROY S.Void fraction distribution for convective boiling flows in single and multiple heater rods assembly[J].Chemical Engineering Science, 2022, 247: 117063.

［16］BALTIS C, GELD C.Experimental investigation of the thermal interactions of nucleation sites in flow boiling[J].International Journal of Heat and Mass Transfer, 2014, 78（11）: 1208-1218.

［17］CHENG M, ZHANG B, LOU J.A hybrid LBM for flow with particles and drops[J].Computers & Fluids, 2017,155（20）: 62-67.

［18］SONG F, WANG W, LI J.A lattice Boltzmann method for particle-fluid two-phase flow[J].Chemical Engineering Science, 2013, 102: 442-450.

［19］LI Q, KANG Q, FRANCOIS M, et al.Lattice Boltzmann modeling of boiling heat transfer: the boiling curve and the effects of wettability[J].International Journal of Heat and Mass Transfer, 2015, 85: 787-796.

［20］YUAN P, SCHAEFER L.Equations of state in a lattice Boltzmann model[J].Physics of Fluids, 2006, 18:042101.

［21］ZHANG T, SHI B, GUO Z, et al.General bounce-back scheme for concentration boundary condition in the lattice-Boltzmann method[J].Physical Review E, 2012, 85: 016701.

［22］FRITZ W.Berechnung des maximal volumes von Dampfblasen[J].Physik Zeitschr, 1935, 36: 379-384.

［23］FENG Y, CHANG F, HU Z, et al.Investigation of pool boiling heat transfer on hydrophilic-hydrophobic mixed surface with micro-pillars using LBM[J].International Journal of Thermal Sciences, 2021, 163: 106814.

［24］GONG S, CHENG P.Lattice Boltzmann simulations for surface wettability effects in saturated pool boiling heat transfer[J].International Journal of Heat and Mass Transfer, 2015, 85: 635-646.

［25］GONG S, CHENG P.Lattice Boltzmann simulation of periodic bubble nucleation, growth and departure from a heated surface in pool boiling[J].International Journal of Heat and Mass Transfer, 2013, 64: 122-132.