基于偶应力理论微纳米Mindlin板的尺度效应分析*

薛江红， 何赞航， 夏 飞， 李泽嵘， 金福松， 杨 鹏

（暨南大学 力学与建筑工程学院 “重大工程灾害与控制”教育部重点实验室，广州 510632）

引 言

随着微小型机械构件的发展，微电子机械系统MEMS、微型传感器、原子力显微镜、微型机器人等逐渐得到广泛应用.在微观尺度下，经典连续介质力学已不再适用，对于微纳米结构的力学分析需要新的理论方法去描述微结构力学性能与微观尺寸参数之间的关系.许多实验表明，当材料尺寸进入微米量级时，材料的刚度和柔度都有所增强，这种现象被称为尺度效应.早期研究中，Fleck等[1]进行了细铜丝的拉伸及扭转实验，在拉伸实验中材料没有出现明显的尺度效应，但在扭转实验中发现无量纲扭矩增加至3倍.为了解释尺度效应，国内外学者相继发展了偶应力理论和应变梯度理论.Toupin[2]在连续力学的基础上引入高阶梯度的基本理论，并假定应变能密度函数依赖于应变梯度和旋转梯度，发展了线弹性偶应力理论； Mindlin[3]提出了依赖于应变张量、变形张量及微观变形梯度的应变能密度函数，讨论了偶应力的典型效应.Fleck和Hutchinson[4]根据Toupin-Mindlin理论框架，发展了偶应力弹塑性理论，并提供了增量形式和全量形式，保证了偶应力和曲率的功的共轭，便于有限元的实现.

2002年，Yang等[5]重新定义曲率，引入偶应力力矩平衡方程，使应变张量和应力张量对称，提出了仅适用于各向同性材料的修正偶应力理论.在修正偶应力的基础上，Simsek[6]和Wang等[7]研究了各向同性梁的非线性弯曲和振动问题，解释了梁和弹性介质之间的相互作用，后者还分析了各向同性梁的后屈曲尺度效应[8].Tsiatas[9]建立了修正偶应力的Kirchhoff板模型.Ma等[10]建立了修正偶应力的Mindlin板模型.Reddy等[11-12]研究并发展了圆板的轴对称问题，并考虑了温度场等多因素下的影响.Gao等[13]建立了基于修正偶应力的三阶剪切板模型.Chen等[14]定义了新的曲率，使得曲率在非对称情况下，偶应力矩对称，成功将修正偶应力理论推广到各向异性材料，并建立了一系列复合材料偶应力微观梁和板模型[15-19].近期，周博等[20]建立了修正偶应力的Bernoulli-Euler微梁模型，能有效描述任意截面形状的振动特性.张大千等[21]建立了微尺度下修正偶应力的Mindlin层合板的热稳定理论模型和有限元模型，研究其在温度载荷与机械载荷共同作用下的尺度效应问题.

上述研究中，考虑尺度效应的梁、板、壳结构的控制方程大多基于能量法得到，从力与变形机制角度分析考虑尺度效应的结构力学性能的研究还较少.本文建立考虑偶应力理论的Mindlin板理论，研究微纳米中厚板在不同边界下的屈曲和振动问题.首先给出包含非对称曲率的微纳米Mindlin板的位移场，引入材料尺寸参数，将应力分为对称和非对称部分，建立了各向同性板的本构关系式.通过外力平衡关系，推导用位移函数和转角函数表示的微纳米Mindlin板的屈曲和振动控制方程.应用分离变量法，求解在四边简支（SSSS）和对边简支、对边固支（SCSC）下微纳米板的屈曲和自由振动的理论解.开发MATLAB编程进行算例分析，将所得的解析解与已有文献的结果、考虑尺度效应的ABAQUS有限元结果进行对比验证，并讨论尺度效应对微纳米板屈曲和自由振动特性的影响.

1 基本理论

考虑一个长为a、宽为b、高为h的微纳米板，如图1所示，用u，v，w来表示板内任意点在x，y，z方向的位移.

图1 微纳米板的位移示意图Fig.1 Schematic diagram of micro-nano plate displacements

根据Mindlin板理论，变形后微纳米板横截面仍为一个平面，用两个转角变量φx，φy来表示板内任一点处法线相对于板中面绕x，y方向的转角.基于此，微纳米板的位移场可以表示为

其中，u0，v0，w0为板的中面位移.不同于宏观尺寸板，微纳米结构中转动分量所引起的应力状态的改变不能忽略，分别用ωx，ωy，ωz来表示三个方向的转动分量为

对于微纳米结构，转动分量描述的是原子之间的相对转动，这种相对转动导致了原子之间曲率的改变.在板壳理论中，垂直于中面方向的正应变和曲率可以忽略不计，即εz= 0，χzz= 0.结合偶应力理论，微纳米板内的应变ε 和曲率χ分别为

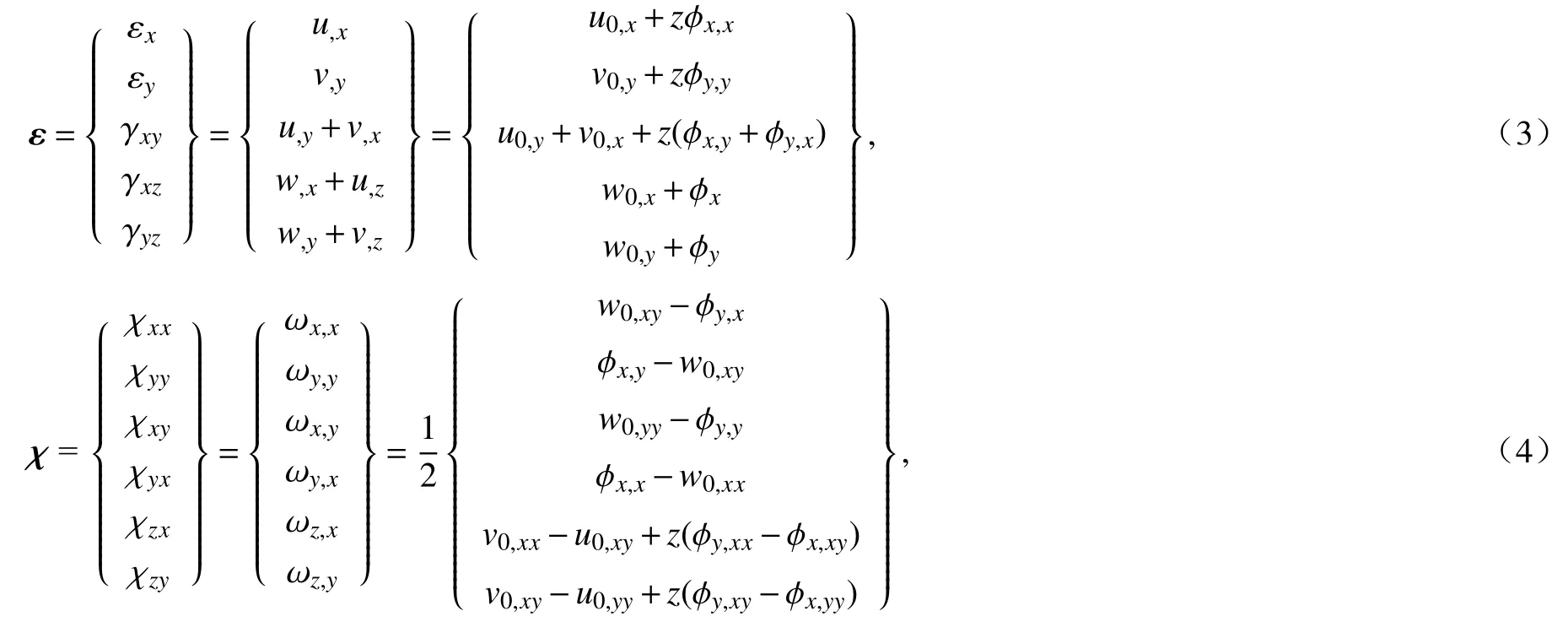
其中χxz=ωx,z=0，χyz=ωy,z=0.由式(4)可以看出，χxy≠χyx，χxz≠χzx，χyz≠χzy，因此曲率χ是非对称的.

在一微纳米弹性体中取任一微元体，将应力和偶应力表示如图2所示.为了获得非对称应力-偶应力的关系，在不计体力情况下，建立微元体的应力平衡微分方程：互等定理不再成立.为此，将应力分量τij分解为对称部分和 非对称部分

图2 微元体各面上的应力和偶应力分布状态Fig.2 The distributions of the stress and the couple stress on the surfaces of a cubic micro element

其中，τst，mij分别为应力和偶应力，ejst为符合张量运算规则的置换符号.式(5)表明，当考虑了偶应力，切应力

其中，ekij为符合张量运算规则的置换符号.式(7)表明，非对称应力可以用偶应力mij表示，展开得

由弹性理论，对称应力和应变的关系可以表示为

其中，G，ν分别为剪切模量和Poisson比， δij为 符合张量运算规则的Kronecker符号.将式(1)和(3)代入式(9)可得如下关系式：

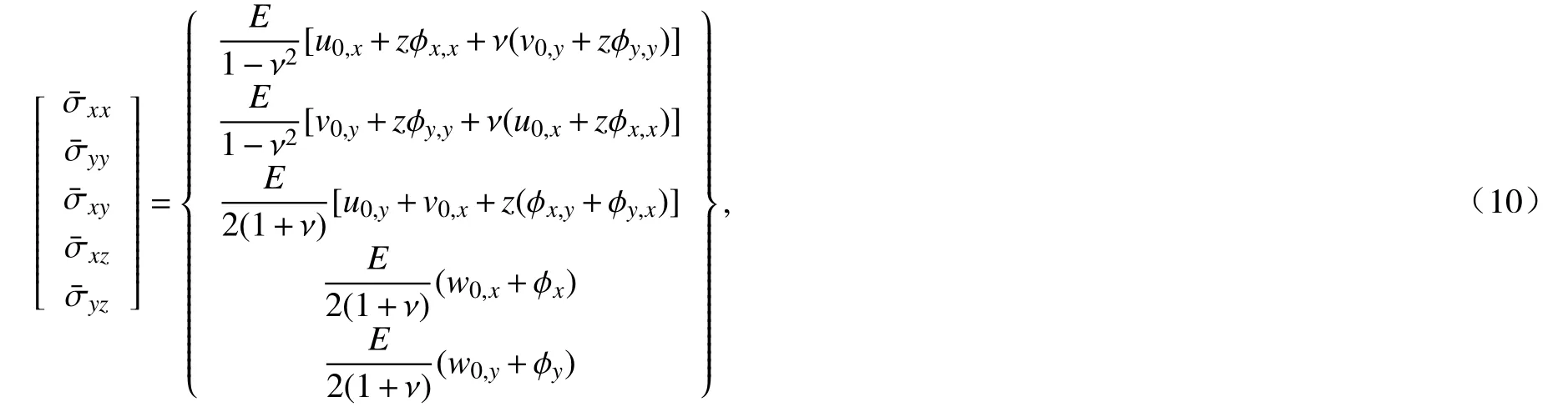
其中，E为材料的弹性模量.根据Fleck-Hutchinson[4]的应变梯度理论，偶应力mij和曲率χij遵循如下关系：

其中，le是材料的长度尺寸参数.将式(2)和(4)代入式(11)即可得到

将式(12)代入式(8)，即得如下关系式：

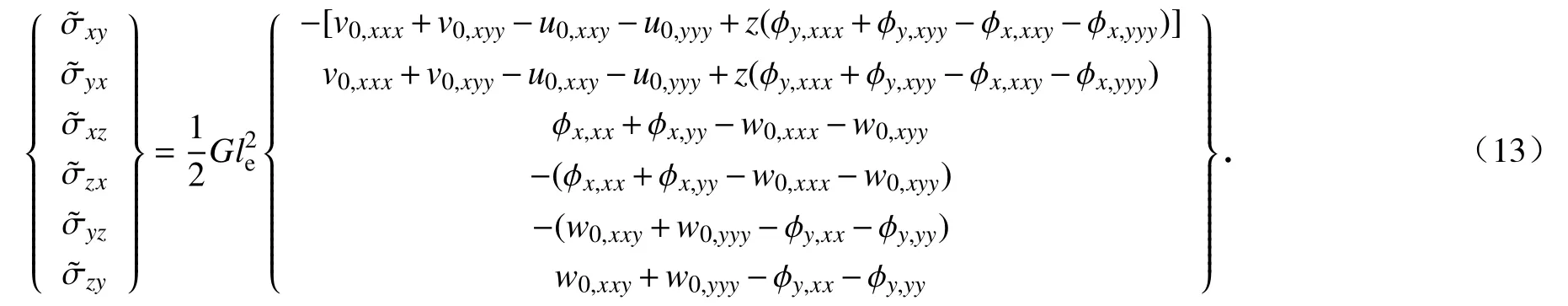
2 微纳米板的控制方程

考虑薄板任一微元体的平衡.为简明起见，只画出该微分块的中面，并将横向荷载和横截面上的内力表示在中面上，其受力情况如图3所示.定义各向同性板的薄膜力N、弯矩M、剪力Q、高阶薄膜力Υ 分别为

图3 各向同性微纳米板微元体的受力平衡状态Fig.3 The force and moment equilibrium of a micro element of the isotropic micro-nano plate

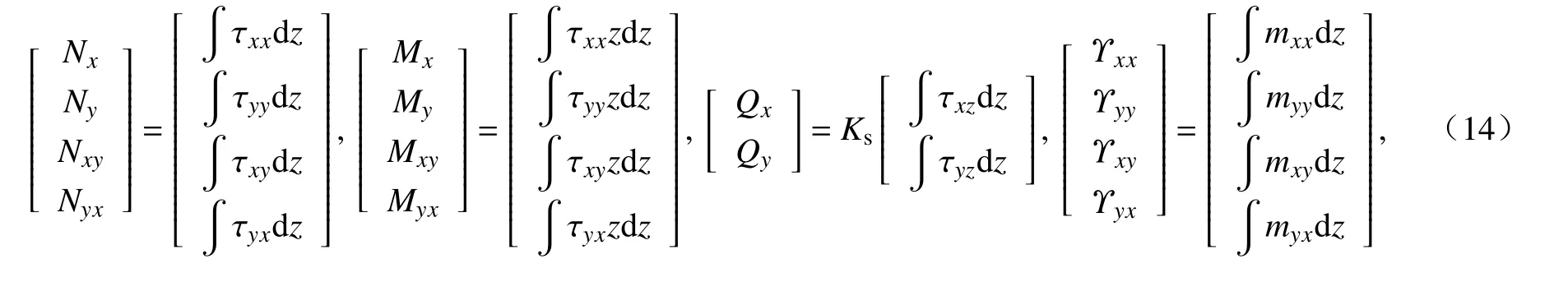
其中，Ks为横向剪切修正系数.引入偶应力后的应力分解为对称应力和非对称应力，内力也分解为对称内力和非对称内力：

考虑所取微分面在x，y，z三个方向上力的平衡和力矩的平衡，并根据w=w0的假设，建立各向同性微纳米板的外力平衡方程：

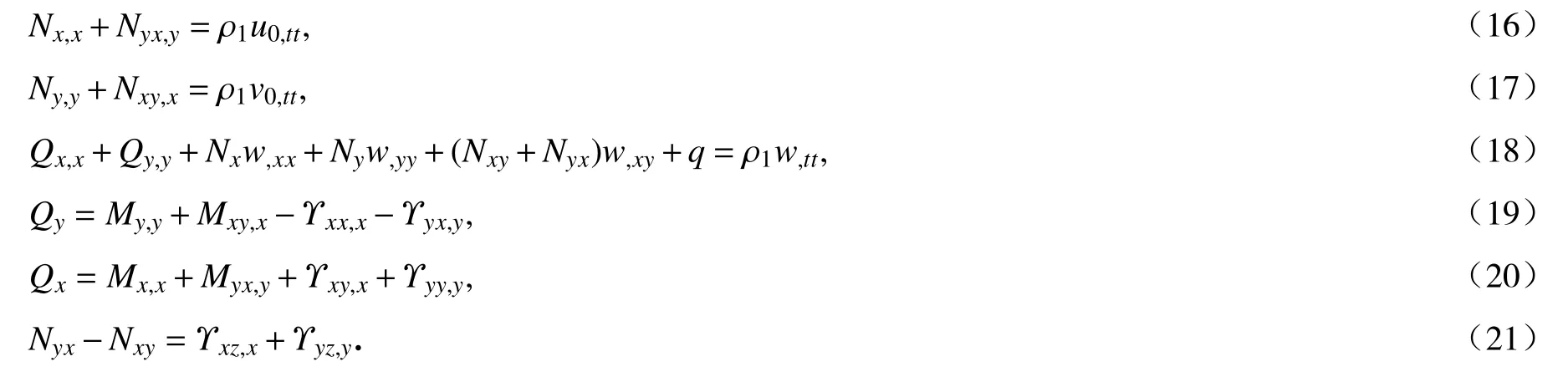
将式(6)、(10)、(12) ～ (15)、(21)代入式(16) ～ (20)，得到用各向同性微纳米板的控制方程：

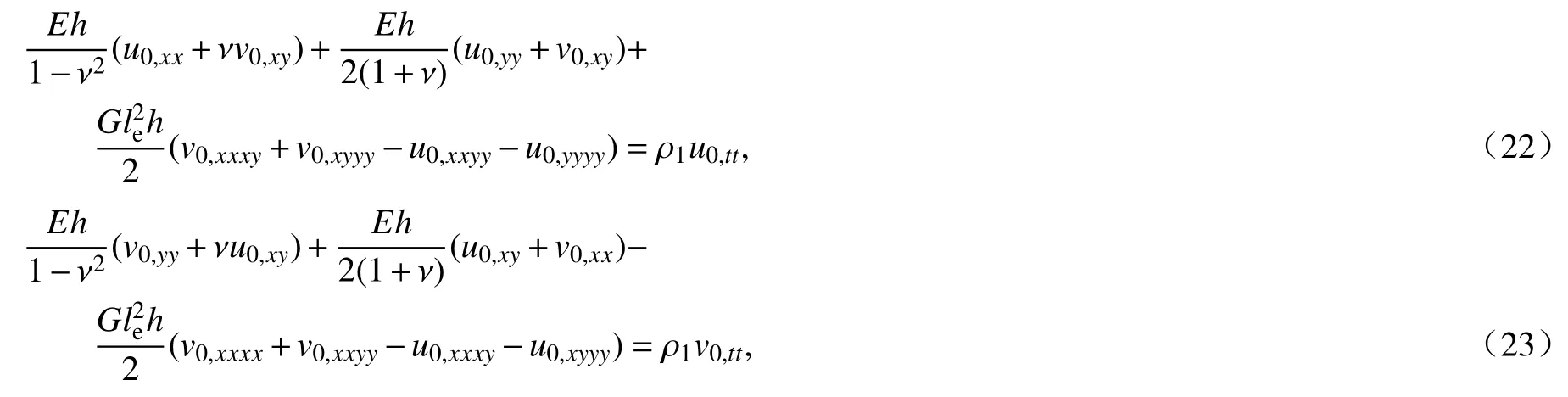
其中，ρ1=ρh，ρ2=ρh3/12，ρ代表板的密度，t代表时间.式(22)、(23)仅与u，v有关，属于平面应力问题，屈曲问题和自由振动问题主要求解式(24) ～ (26).

3 求解方法

本文考虑两种边界条件下的微纳米矩形板：

SSSS矩形板的边界条件如下：

在x= 0和x=a处，

在y= 0和y=b处，

SCSC矩形板的边界条件如下：

在x= 0和x=a处，

在y= 0和y=b处，

采用分离变量法，将位移函数w和转角函数φx，φy在x和y方向以及时间域上进行分离，分析在两种边界条件和不同参数下的矩形板（图4）的屈曲问题和自由振动问题.

图4 矩形板的边界条件Fig.4 Boundary conditions for the rectangular plate

设位移表达式为一个单重三角函数：

3.1 屈曲求解

将式(31)代入式(24) ～ (26)并联立，可得

将式(33)回代入式(31)，结合控制方程式(24)和(25)，可以得出振幅系数之间的关系式，最后利用边界条件(27)、(28)或者条件(29)、(30)建立待定未知数系数矩阵，并令其等于0，通过编写MATLAB程序可求出不同边界条件下的临界屈曲荷载Nx.

3.2 振动求解

将式(31)代入式(24) ～ (26)并联立，可得

其中，RV是与板的几何参数、材料参数有关的3 × 3的矩阵；M为板的ω2的系数的矩阵，主要与ρ1有关.与屈曲求解不同的是，控制方程中不考虑面内荷载的作用，建立的是包含ω2的系数矩阵，也即|RV-ω2M| = 0，同样根据得到的模态根以及结合边界条件(27)、(28)或者条件(29)、(30)，通过编写MATLAB程序得到不同边界条件下的固有频率ω.

4 算例分析和讨论

本文采用解析法计算不同边界、不同参数下微纳米中厚板的屈曲问题和自由振动问题.板的几何参数：a=200 µm，b= 200 µm，h= 5 µm，le= 0 ～h；材料参数：E= 6.98 GPa，ν = 0.25，ρ = 1 578 kg/m3[22]，且Ks= 1.

为了验证理论的准确性，将本文理论解分别与Tsiatas解[9]、ABAQUS有限元解进行了对比.基于偶应力理论，Tsiatas[9]建立的是未考虑剪切效应的Kirchhoff板模型，由Tsiatas理论可推导出SSSS边界条件下，微纳米薄板的屈曲临界荷载和自由振动固有频率的求解表达式：

对于SSSS的板，将本文理论解与由式(35)、(36)所得Tsiatas解进行对比，以验证本文理论的正确性.

在ABAQUS中建模时，建立微米量级板的壳模型，采用四节点曲壳单元S4R将实体模型划分为有限元模型，如图5所示.在板的四周分别施加SSSS或SCSC的边界条件，在屈曲分析步中，在板两端施加1 N/m的线压缩荷载，故输出的特征值即为屈曲荷载.对于不考虑剪切效应的各向同性材料，考虑尺度效应相当于增强材料的刚度，在ABAQUS有限元模型中需要对材料的弹性模量进行修正，修正后的弹性模量为(详见附录)

图5 微纳米板的有限元网格示意图Fig.5 Meshing of the micro-nano plate

将修正后的弹性模量输入ABAQUS的材料参数中，即可得到不同尺度效应下的微纳米板的屈曲荷载和固有频率的有限元解.

4.1 屈曲分析

4.1.1 厚长比的影响

图6给出了当板长度和宽度(a=b= 200 µm)、尺寸参数(le/h= 0.5)一定时，在SSSS和SCSC两种边界条件下微纳米板的临界屈曲荷载的理论解和有限元解随厚长比的变化情况.从图6可以看出，理论解与Tsiatas解和有限元解比较吻合，相对误差控制在10%以内，验证了本文模型的准确性.同时，随着板的厚长比的增加，两种边界条件下板的临界屈曲荷载均不断增加；SCSC微纳米板的临界屈曲荷载始终大于SSSS微纳米板的临界屈曲荷载，这是由于SCSC边界有一对边是固支，限制了转动自由度，因此可以承受更高的屈曲荷载.

图6 SSSS和SCSC边界下微纳米板的临界屈曲荷载随厚长比的变化Fig.6 Effects of the relative depth on the buckling load of the micro-nano plate under SSSS and SCSC

4.1.2 尺寸参数的影响

图7给出了当板的长度和宽度一定(a=b= 200 µm)时，在SSSS和SCSC两种边界条件下，微纳米板的临界屈曲荷载随相对尺寸参数的变化情况.从图7可以看出，对厚长比h/a一定的板，随着尺寸参数的增加，临界屈曲荷载也同样增大.其中，le/h=1的临界荷载约是le/h=0的10倍，也即当尺寸参数与板厚的量级相同时，得到的临界荷载比未考虑尺度效应的板的结果大10倍，这说明尺度效应对板承载力的增强十分明显，此时尺度效应不能被忽略.同时，对比两个不同边界，对于任一给定的尺寸参数le/h，SCSC微纳米板的临界屈曲荷载均约为SSSS微纳米板的1.6倍，这表明尺度效应对板承载能力的增强作用基本不受边界改变影响.

图7 不同厚长比下，微纳米板临界屈曲荷载随尺寸参数的变化：（a）SSSS；（b）SCSCFig.7 Effects of the dimensional parameters on the buckling load of the micro-nano plate for different thickness-to-length ratios: (a) SSSS; (b) SCSC

4.2 振动分析

4.2.1 剪切效应的影响

图8给出了当板的长度和宽度一定(a=b= 200 µm)时，在不同的尺寸参数下，SSSS微纳米板的固有频率随厚长比变化的曲线.其中，ωP表示本文求得的自由振动固有频率，ωT表示对应参数下的Tsiatas解，理论解和Tsiatas解之间的差值比为η = (ωT-ωP)/ωP.为了便于分析，在图的左半部分给出了相同情况下剪切解与经典解差值比η随着厚长比的变化曲线.

图8 不同尺寸参数下，SSSS微纳米板固有频率随厚长比的变化Fig.8 Effects of the thickness-to-length ratio on the natural frequency of the SSSS micro-nano plate for different values of dimensional parameters

从图8可以看出，无论是否考虑尺度效应，固有频率均随着厚长比的增加而增大；随着尺寸参数的增加，固有频率也不断增大.图8表明，当微纳米板的相对厚度较小时(h/a≤0.1)，理论解和Tsiatas解之间的相对差值η非常小，验证了本文理论的正确性.随着微纳米板的厚长比的增加，差值比η不断增加，由于经典理论忽略了横向剪切变形，板的厚度越大，这种忽略带来的两种理论间的差值越大.同时看出，两种理论间的差值随着尺寸参数le/h增加而增大，这是由于在剪切效应中引入了转角函数，同时本文又考虑了用转动分量来描述原子之间的相对转动，引入了非对称曲率的概念.材料的尺寸参数一般都是微纳米量级的，从曲率和偶应力之间的本构关系（式（12））可以看出，曲率对于微观结构的影响很大，曲率连同面外剪切应变，共同产生了剪切效应这一宏观现象.因此，相对于宏观板，考虑了尺度效应的微纳米板的剪切效应更明显.

4.2.2 长宽比和尺寸参数的影响

图9给出了当板的长度和厚度一定(a= 200 µm,h= 5 µm)时，不同的尺寸参数下，SSSS和SCSC微纳米板的固有频率随长宽比变化的曲线.从图9(a)中可以看出，对于尺寸参数le/h给定的SSSS板，随着长宽比的增加，固有频率持续增大；对于尺寸参数le/h给定的SCSC板，随着长宽比的增加，固有频率则不断增大.对于长宽比a/b给定的SSSS和SCSC两种边界条件下的板，随着尺寸参数的增加，固有频率均不断增大；当尺寸参数le从0增大至h，板的固有频率约为前者的3倍，说明当板尺寸为微纳米量级时，尺度效应对于微纳米板自由振动特性的影响很大.同时，对比两种边界下的数值，可以得出和4.2.1小节相似的结论，即尺度效应对板的振动特性的影响基本与边界条件无关.

图9 不同尺寸参数下，微纳米板固有频率随长宽比的变化：（a）SSSS; （b）SCSCFig.9 Effects of the aspect ratio on the natural frequency of the micro-nano plate for different dimensional parameters: (a) SSSS; (b) SCSC

5 结 论

本文建立了考虑偶应力的各向同性微纳米结构的Mindlin板理论，进行了微纳米板的屈曲分析和自由振动分析.运用偶应力理论和Mindlin板理论建立了各向同性微纳米板的本构方程，利用力和变形的协调机制推导出外力共同作用下各向同性微纳米板的控制方程.开发MATLAB程序求解在SSSS和SCSC边界条件下，各向同性板的临界屈曲荷载和固有频率，为验证所建立理论的准确性，将本文理论解和已有解、考虑了尺度效应的有限元解进行对比验证，结果非常吻合.研究表明：

1）对于各向同性微纳米板，不考虑尺度效应会导致对板临界屈曲荷载和固有频率的低估.对于屈曲问题，当尺寸参数le从0增大至h，板的临界屈曲荷载约为前者的10倍；对于自由振动问题，当尺寸参数le从0增大至h，板的固有频率约为前者的3倍.

2）随着厚长比和长宽比(一定范围内)的增加，板的临界屈曲荷载和固有频率不断增大，剪切理论解与经典解之间的差值也越来越大.相对于宏观板，考虑了尺度效应的微纳米板的剪切效应更明显.

3）微纳米板的屈曲解和自由振动解随着边界条件的改变而改变，一般来说，边界约束越强，得到的数值结果越大；尺度效应对板的屈曲和自由振动特性的影响基本与边界条件无关.

附 录

以下给出式(37)的推导过程.根据经典板壳理论，板的挠度w仅为x，y的函数，因此不计中面的薄膜变形与横向剪切变形的板的三个方向上的位移可以表示为

经典理论中，转动位移ωx，ωy，ωz与式(2)一样.将式(A1)、式(2)代入式(3)、(4)，应变和曲率可以表示为

将式(A2)、(A3)分别代入式(9)、(11)，可得应力-位移、偶应力-曲率的关系：

将式(A4)、(A5)、(19)、(20)代入式(18)，得到各向同性微纳米板的控制方程：

式中

经典板壳理论中各向同性微纳米板的控制方程为

结合式(A6)、(A7)，尺度效应对刚度的增强效应为

即对于各向同性材料，考虑尺度效应相当于修正了弹性模量：

需要注意的是，考虑尺度效应实际上是考虑偶应力的影响.由式(16) ～ (20)可以看出，偶应力的影响主要存在于力矩的平衡和z方向力的平衡中，对x，y方向力的平衡，即薄膜力的平衡是不产生影响的.因此，偶应力的影响主要是反映在弯曲问题的折算模量上，对薄膜部分折算模量的影响可以忽略不计.在此弯曲问题中同时考虑薄膜力，本文附录所推导的折算模量依然适用.

参考文献（ References ）：

［1］FLECK N A, MULLER G M, ASHBY M F, et al.Strain gradient plasticity: theory and experiment[J].Acta Metallurgica et Materialia, 1994, 42（2）: 475-487.

［2］TOUPIN R A.Elastic materials with couple-stresses[J].Archive for Rational Mechanics and Analysis, 1962,11（1）: 385-414.

［3］MINDLIN R D.Influence of couple-stresses on stress concentrations[J].Experimental Mechanics, 1963, 3（1）: 1-7.

［4］FLECK N A, HUTCHINSON J W.A phenomenological theory for strain gradient effects in plasticity[J].Journal of the Mechanics and Physics of Solids, 1993, 41（12）: 1825-1857.

［5］YANG F, CHONG A C M, LAM D C C, et al.Couple stress based strain gradient theory for elasticity[J].International Journal of Solids and Structures, 2002, 39（10）: 2731-2743.

［6］SIMSEK M.Nonlinear static and free vibration analysis of microbeams based on the nonlinear elastic foundation using modified couple stress theory and He’s variational method[J].Composite Structures, 2014, 112（1）: 264-272.

［7］WANG Y G, LIN W H, LIU N.Nonlinear bending and post-buckling of extensible microscale beams based on modified couple stress theory[J].Applied Mathematical Modelling, 2015, 39（1）: 117-127.

［8］WANG Y G, LIN W H, ZHOU C L, et al.Thermal postbuckling and free vibration of extensible microscale beams based on modified couple stress theory[J].Journal of Mechanics, 2015, 31（1）: 37-46.

［9］TSIATAS G C.A new Kirchhoff plate model based on a modified couple stress theory[J].International Journal of Solids and Structures, 2009, 46（13）: 2757-2764.

［10］MA H M, GAO X L, REDDY J N.A non-classical Mindlin plate model based on a modified couple stress theory[J].Acta Mechanica, 2011, 220（1/4）: 217-235.

［11］ZHOU S S, GAO X L.A nonclassical model for circular Mindlin plates based on a modified couple stress theory[J].Journal of Applied Mechanics, 2014, 81（5）: 1-8.

［12］REDDY J N, BERRY J.Nonlinear theories of axisymmetric bending of functionally graded circular plates with modified couple stress[J].Composite Structures, 2012, 94（12）: 3664-3668.

［13］GAO X, HUANG J, REDDY J.A non-classical third-order shear deformation plate model based on a modified couple stress theory[J].Acta Mechanica, 2013, 224（11）: 2699-2718.

［14］CHEN W J, LI L, XU M.A modified couple stress model for bending analysis of composite laminated beams with first order shear deformation[J].Composite Structures, 2011, 93（11）: 2723-2732.

［15］李莉, 陈万吉, 郑楠.修正偶应力理论层合薄板稳定性模型及尺度效应[J].工程力学, 2013, 30（5）: 1-7.（LI Li,CHEN Wanji, ZHENG Nan.Model of composite laminated thin plate based on modified couple stress theory and buckling analysis of scale effect[J].Engineering Mechanics, 2013, 30（5）: 1-7.（in Chinese））

［16］李莉, 陈万吉, 李小鹏.修正偶应力理论层合薄板自由振动模型及尺度效应[J].大连理工大学学报, 2013, 53（3）: 313-321.（LI Li, CHEN Wanji, LI Xiaopeng.Free vibration model of composite laminated thin plate based on modified couple stress theory and scale effects[J].Journal of Dalian University of Technology, 2013, 53（3）: 313-321.（in Chinese））

［17］CHEN W J, LI X P.Size-dependent free vibration analysis of composite laminated Timoshenko beam based on new modified couple stress theory[J].Archive of Applied Mechanics, 2013, 83（3）: 431-444.

［18］陈万吉, 任鹤飞.基于新修正偶应力理论的Mindlin层合板自由振动分析[J].工程力学, 2016, 33（12）: 31-37, 43.（CHEN Wanji, REN Hefei.Free vibration analysis of a laminated composite Mindlin plate based on new modified couple stress theory[J].Engineering Mechanics, 2016, 33（12）: 31-37, 43.（in Chinese））

［19］陈万吉, 薛继伟.新修正偶应力理论Reddy型层合板稳定分析[J].计算力学学报, 2017, 34（2）: 162-167.（CHEN Wanji, XUE Jiwei.Stability analysis of composite laminated Reddy plate based on new modified couple-stress theory[J].Chinese Journal of Computational Mechanics, 2017, 34（2）: 162-167.（in Chinese））

［20］周博, 王志勇, 赵飞, 等.Bernoulli-Euler微梁振动特性的尺寸效应[J].中国石油大学学报(自然科学版), 2021, 45（1）:151-157.（ZHOU Bo, WANG Zhiyong, ZHAO Fei, et al.Size effect of vibration characteristics of Bernoulli-Euler microbeam[J].Journal of China University of Petroleum(Edition of Natural Science), 2021, 45（1）: 151-157.（in Chinese））

［21］张大千, 王云鹏, 王玺鉴.各向异性修正偶应力Mindlin层合板的有限元热稳定性分析[J].沈阳航空航天大学学报,2020, 37（2）: 10-20.（ZHANG Daqian, WANG Yunpeng, WANG Xijian.Study on thermal stability of anisotropic modified coupled stressed Mindlin laminates by finite element methods[J].Journal of Shenyang Aerospace University, 2020, 37（2）: 10-20.（in Chinese））

［22］PAGANO N J.Exact solutions for rectangular bidirectional composites and sandwich plates[J].Journal of Composite Materials, 1970, 4（1）: 20-34.