一题多解在初中数学教学中的应用
山东省邹平市梁邹实验初级中学 张婷丽
一题多解指采用不同的解法解答同一道习题。初中数学教学开展一题多解教学活动时既要做好相关习题的筛选,又要根据例题的难易程度给学生预留一定的时间,鼓励学生思考、讨论,激活初中数学课堂教学,使学生在活泼愉悦的氛围中,找到更简便的解题方法。
一、用于比较分式大小
比较分数大小是初中数学中一类非常重要的题型。常用的解题思路有三种:第一种,将两个分数作差,比较差与0的大小;第二种,将两个分式做商,比较商与1的大小;第三种,选取一个中间的分式,以中间的分式为媒介进行比较。
A.M<N B.M>N C.M=N D.不确定
解法一:作差法
解法二:特殊值法
两种方法都能选择出正确答案。第一种方法为传统方法,比较容易想到,但是计算稍微复杂。第二种方法通过简单的计算便可得出正确答案,需要学生具备灵活的思维。
二、用于解答绝对值方程
解一元一次方程是学生必须掌握的一个基本知识。初中数学部分一元一次方程的习题中带有绝对值,难度较大。该类习题的解题思路并不唯一。在教学中为了更好地拓展学生的视野,使学生能具体问题具体分析,选择高效的解题方法,提高解题效率,教师应运用一题多解给学生带来解题启发。
例:解方程|2x+19|=7x+31
解法一:分类讨论
解法二:对比分析法

解法一是学生非常容易想到的解题思路,先分类讨论,而后对方程的解进行合理的取舍,相对来说计算较为复杂。解法二通过观察给出的方程,巧妙地加以切入,有效避免了分类讨论,解题效率明显提高。教师在教学中要引导学生多注重应用解法二解题。
三、用于证明几何问题
几何证明题常出现在初中数学各类测试中的大题中,占有较高的分值。该类习题的解题思路多种多样,常用到知识点有全等三角形、相似三角形等。在初中数学教学中为使学生掌握几何证明问题的相关思路,教师应结合具体的习题,鼓励学生不满足于一种解法,注重一题多解,更好地拓展学生的思维与解题能力。
例:如图1所示,等腰△ABC中,AB=AC,P是底边BC上的任意一点,过点P分别作AB,AC的垂线,垂足为点D、点E,过点B作AC的垂线,垂足为点F。求证:PD+PE=BF。
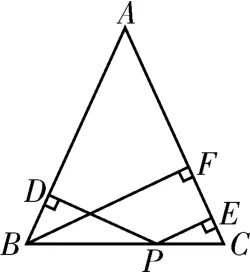
图1
证法一:三角形全等法
过点P作BF的垂线,垂足为点H(见图2)。因为BF⊥AC,PE⊥AC,则四边形HPEF为矩形,所以HF=PE。又HP∥FE,所以∠C=∠HPB,而在△ABC中AB=AC,所以∠C=∠ABC,所以∠ABC=∠HPB。又∠BDP=∠PHB=90°,BP=PB,所以△BHP≌△PDB,所以BH=PD,而BH+HF=BF,所以PD+PE=BF,得证。
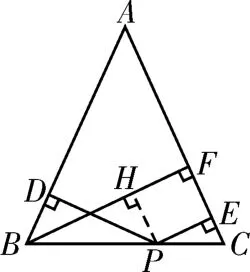
图2
证法二:面积法

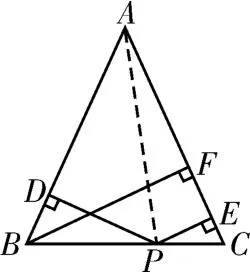
图3
证法一虽然涉及的知识点较多,但学生非常容易想到,在教学中要求学生掌握该种方法。证法二虽然较为简单,但是不容易想到,教学中应多给予学生引导,使其在以后的证明中尝试着应用。
四、用于突破抛物线难题
抛物线难题常出现在压轴题中。教师在教学中为提高学生解答该类习题的自信心,应结合具体的习题进行一题多解,为学生剖析不同解题方法的解题思路,进一步提高学生认识,使其把握解题的关键。
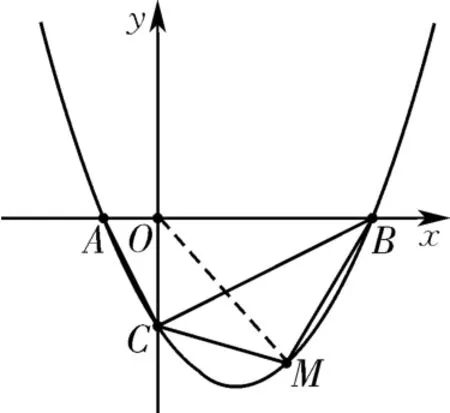
图4
解法一:割补法
解法二:平行线法
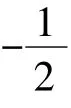

图5

第一种解题方法较为简单,但是不容易想到。第二种解题方法难度较大,应用的知识点较多,对学生的综合能力要求较高。教师在教学中要求学生根据自身的实际情况,掌握其中一种解题方法即可。
五、结语
初中数学教学中为提高学生的一题多解意识,更好地锻炼学生的思维与解题能力,应结合学生实际选择由易到难的习题,循序渐进,为学生展示不同习题的多种解法,拓展学生视野,使其能够结合自身的实际情况加以掌握、应用。

