XMQ6182G型客车低频轰鸣声仿真分析与抑制

盛精， 向铁明， 王梦光， 卓建明， 黄丛林， 韩勇

(1. 厦门理工学院 福建省客车先进设计与制造重点实验室， 福建 厦门 361024； 2. 厦门金龙联合汽车工业有限公司， 福建 厦门 361023； 3. 神龙汽车有限公司 襄阳工厂， 湖北 襄阳 441004)

低频轰鸣声是一种常见的车内噪声源，严重影响着驾乘的舒适性[1-3].作为整车核心部件的白车身(body in white，BIW)，其动力学特性在很大程度上影响着整个车身特性，可直接反映整车的舒适性[4-5].当车内空腔声学模态频率、车身结构模态频率与外界激励频率接近时，容易引起结构模态与空腔声学模态的强耦合[6]，从而在车内产生低频声学轰鸣.研究者通常对白车身、车内空腔进行模态分析，以寻求解决途径.颜伏伍等[7]经噪声测试、模态分析后，认为客车室内轰鸣声来源于后悬架稳定杆的共振，通过结构的改进降低噪声.Cao 等[8]对某轿车轰鸣声进行研究，对车身顶部结构进行优化，降噪效果明显.李伟等[9]对壁板结构和声腔耦合开展研究，对某微型客车结构进行优化和试验验证，提高乘坐舒适性.杨仕祥等[10]运用实验测试和数值模拟方法，探讨某商用车怠速轰鸣问题，优化发动机悬置的布置.Wu 等[11]对某货车加速轰鸣声产生的机理进行分析.Sim等[12]对客车低频噪声的来源进行探究.

上述文献对低频轰鸣声的研究大多集中于轿车或轻型客车，关于外形庞大、结构复杂的大型客车低频轰鸣声问题可借鉴的解决方案较少.基于此，本文通过振动和噪声测试，分析XMQ6182G型客车轰鸣声的产生原因，并根据测试和仿真结果提出相应的改进措施.

1 模态分析原理

1.1 结构模态分析原理

车身结构系统的动力学方程为

(1)

式(1)中：M，K，C分别为系统的质量矩阵、刚度矩阵和阻尼矩阵；ξ，p(t)分别为结构位移和动载荷向量.

对于车身结构系统，由于C=0，p(t)=0，则方程(1)的特征方程为

K-ω2M=0.

(2)

式(2)中：ω为车身结构的固有频率.

由式(2)可得车身结构模态的固有频率和对应频率的模态振型.

1.2 声学模态分析原理

理想条件下，车内的声压满足三维声学波动方程，即

(3)

式(3)中：∇2为拉普拉斯算子；Ps为声场中目标点的声压函数，Ps=Ps(x，y，z)；c0为声波传播速度.

车内空腔声压具有简谐波特征，设定其声场任意一点的声压值(声压函数)为Ps=P·exp(jωt)，其中P为声压幅值，P=P(x，y，z).则式(3)变换为

∇2Ps+k2P=0.

(4)

式(4)中：k为波数，k=ω/c0.

对车内空腔声场区域进行离散化，可得声学有限元方程，即

(5)

式(5)中：Ma，Ka，Ca分别为单元流体的质量矩阵、刚度矩阵和阻尼矩阵；pe为单元节点声压.

将边界条件设为刚性边界条件，式(5)的特征方程为

(6)

式(6)中：ωs为声腔声学固有频率.

由式(6)可得车内空腔声学模态固有频率(特征值)及其相应的模态振型(特征向量).

2 车内轰鸣声分析

2.1 车内轰鸣声的产生机理

车室内任一点K的声压值可表示为

(7)

式(7)中:Fj为激励力，j=1，…，m，m为传递路径数；HK，j为噪声传递函数.

由式(7)可知，系统响应与各传递路径上的激励力、噪声传递函数有关.因此，在激励力不变的情形下，通过对传递路径上的相关零部件结构进行优化，即可对车内轰鸣声(噪声)进行控制.

2.2 车内噪声的主观评价

以XMQ6182G型客车为研究对象，该车发动机后置，后轮驱动，发动机为4冲程6缸柴油机，悬架系统中弹簧为钢板弹簧，轮胎为双线真空胎.对XMQ6182G型客车的车内噪声进行主观评价，当客车在30～80 km·h-1匀速行驶时，驾驶位有明显的轰鸣声.

2.3 噪声和振动测试

噪声和振动测试均采用LMS数据采集系统，在车速(v)分别为30，50，80 km·h-1(匀速，空调关闭)的3种工况(工况1～3)下进行.根据噪声测试标准，噪声测试的测点布置于驾驶位人耳高度处，如图1所示.振动测试的测点布置于轴头和板簧上.轴头和板簧的测点布置，如图2，3所示.

图1 噪声测试的测点布置Fig.1 Layout of measuring points of noise test

(a) 前左轴头 (b) 后左轴头 图2 轴头的测点布置Fig.2 Layout of measuring points of axle head

(a) 前左板簧 (b) 后左板簧 图3 板簧的测点布置Fig.3 Layout of measuring points of leaf spring

3种工况下驾驶位噪声频谱，如图4所示.图4中：fd为驾驶位噪声频率；L为驾驶位噪声声压级.由图4可知：车内噪声的低频成分很大；在3种工况下，当驾驶位噪声频率约为14.0 Hz时，出现驾驶位噪声声压级峰值.

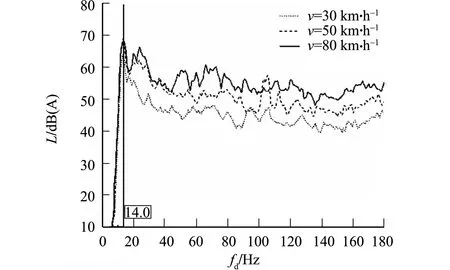
图4 3种工况下驾驶位噪声频谱Fig.4 Spectrum of driving position noise under three working conditions

汽车行驶时，振动能量一方面来自发动机及传动系统[13-14]，另一方面来自轮胎、悬架系统等[15-16].发动机激励频率fe为

(8)

式(8)中:N，n，c分别为发动机转速、发动机气缸数量和冲程系数.

3种工况下发动机的激励频率，如表1所示.

表1 3种工况下发动机的激励频率Tab.1 Excitation frequency of engine under three working conditions

由表1可知：当车速分别为30，50，80 km·h-1时，对应的发动机激励频率分别为50.0，62.5，73.5 Hz；3种工况下发动机激励频率都偏离车内驾驶位噪声频率峰值(fd=14.0 Hz)，故驾驶位轰鸣声与发动机激励无关.

3种工况下轴头和板簧的Y向振动频谱，如图5～7所示.图5～7中：a为振动加速度；fY为Y向振动频率.由图5～7可知：在3种工况下，轴头和板簧的Y向振动频率峰值约为14.0 Hz.进一步对悬架进行偏频测试，结果如图8所示.由图8可知：后左轴头和板簧的Y向振动频率峰值为14.2 Hz，与驾驶位噪声频率峰值相近，故判断驾驶位轰鸣声主要来自路面激励.

图5 轴头和板簧的Y向振动频谱(工况1)Fig.5 Y-direction vibration spectrum of axle head and leaf spring (condition 1)

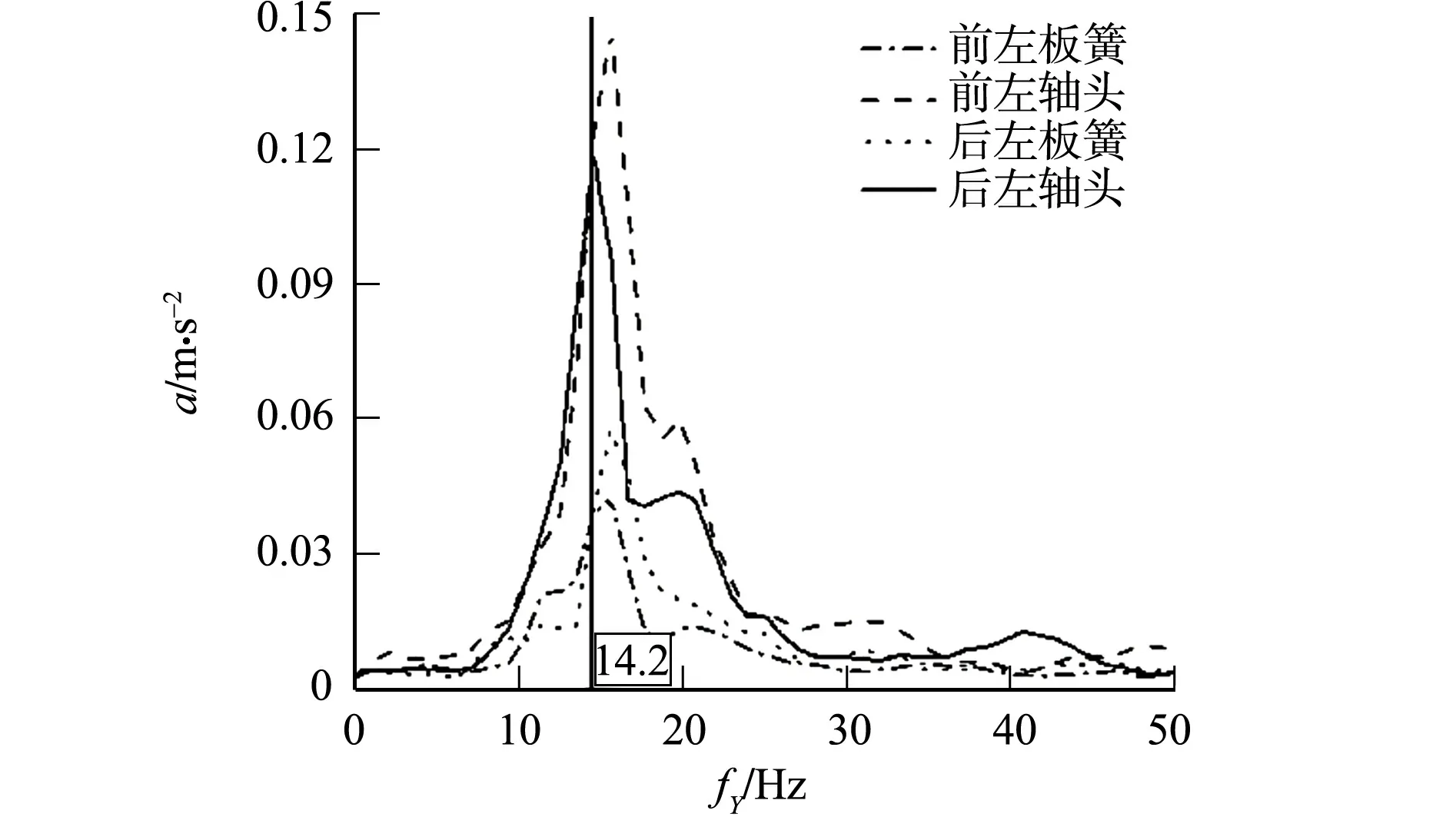
图6 轴头和板簧的Y向振动频谱(工况2)Fig.6 Y-direction vibration spectrum of axle head and leaf spring (condition 2)

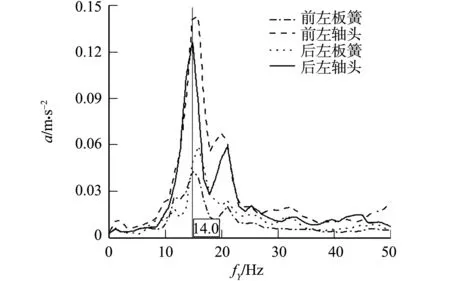
图7 轴头和板簧的Y向振动频谱(工况3)Fig.7 Y-direction vibration spectrum of axle head and leaf spring (condition 3)

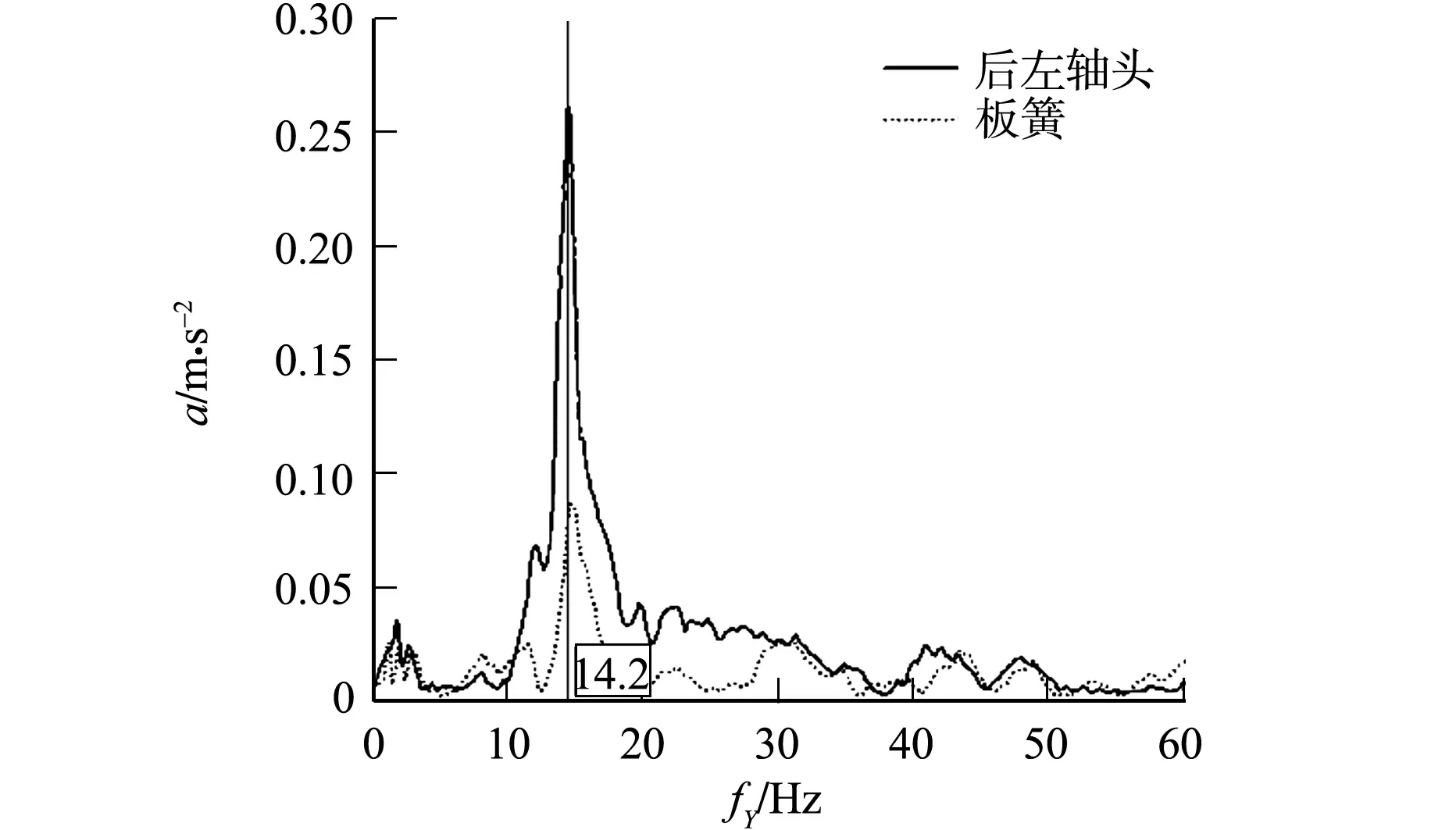
图8 偏频测试结果Fig.8 Frequency offset test results

3 模态分析

采用HyperMesh软件构建XMQ6182G型客车的车身结构(白车身)和车内空腔有限元模型，如图9，10所示.

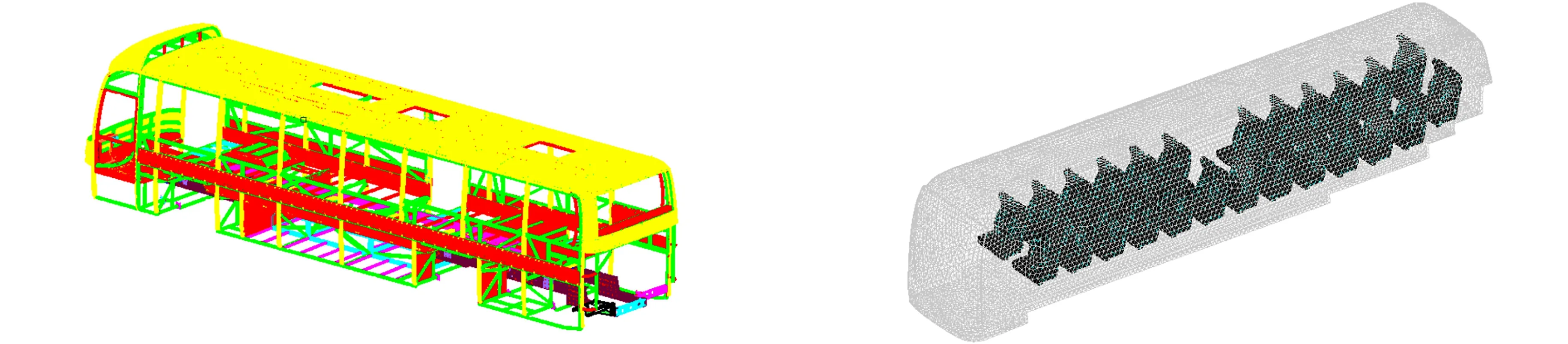
图9 白车身有限元模型 图10 车内空腔有限元模型 Fig.9 Finite element model of BIW Fig.10 Finite element model of interior cavity

结构模态频率仿真值与实验值的对比，如表2所示.声学模态频率仿真值与实验值的对比(前3阶)，如表3所示.表2，3中：fb，s，fb，e分别为白车身结构模态频率的仿真值和实验值；η1为白车身结构模态频率仿真值与实验值的误差；fc，s，fc，e分别为车内空腔声学模态频率的仿真值与实验值；η2为车内空腔声学模态仿真值与实验值的误差.

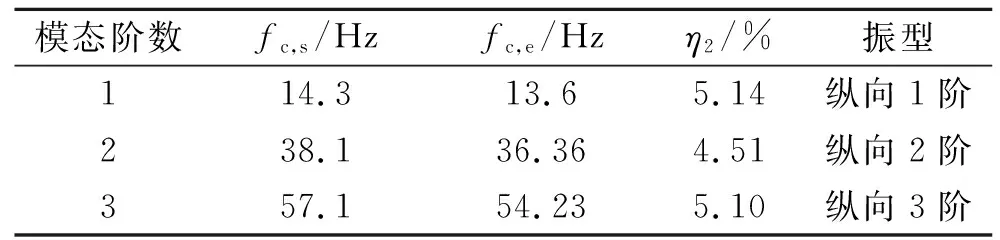
表3 声学模态频率仿真值与实验值的对比(前3阶)Tab.3 Comparison of acoustic mode frequency simulation values and experimental values (first three orders)

由表2，3可知：结构模态频率和声学模态频率仿真值与实验值的误差均小于6.00%，在工程误差许可范围之内，表明构建的有限元模型具有有效性.

由仿真分析可知，白车身第3阶结构模态频率与车内空腔第1阶声学模态频率较为接近，易产生声固耦合共振.

白车身第3阶结构模态振型图，如图11所示.由图11可知：顶盖在14.4 Hz出现局部模态.车内空腔第1阶声学模态振型图，如图12所示.

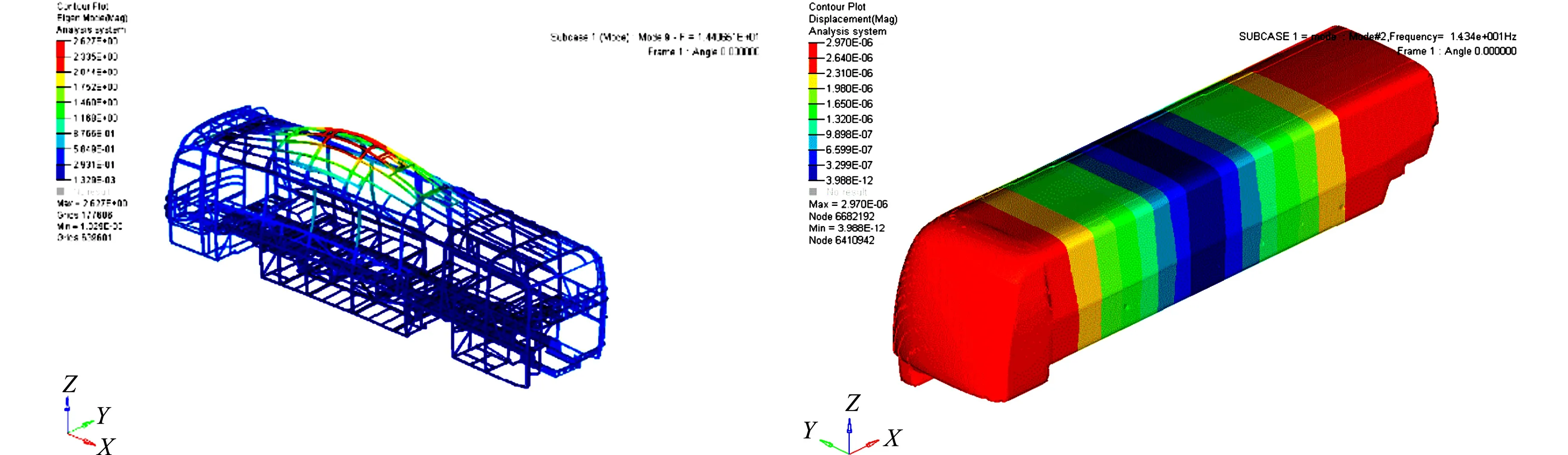
图11 白车身第3阶结构模态振型图 图12 车内空腔第1阶声学模态振型图 Fig.11 Third-order structural modeshape diagram of BIW Fig.12 First-order acoustic mode shape diagram of interior cavity

由图4，8，11，12可知：当路面激励频率约为14.0 Hz时，出现驾驶位噪声声压级峰值，此时，激发白车身第3阶结构模态，引起顶盖和车内空腔产生声固耦合共振，产生轰鸣现象.

4 轰鸣声的抑制

XMQ6182G型客车产生的轰鸣声主要来自车身结构的响应.因此，可以从3个方面对车内轰鸣声进行控制：1) 控制激励源；2) 调节车内空腔声学模态；3) 改变车身结构模态.比较客车的生产制造成本、制造工艺等因素，拟从加强顶盖刚度入手，通过适当的结构改进，改变车身结构模态频率，阻隔结构模态与声学模态的耦合作用，降低或消除车内轰鸣声.

根据白车身第3阶结构模态(图11)，进行顶盖结构改进，有以下2个改进措施.

1) 改进措施1.顶盖最大振动位移发生在第3根弧杆处，故将第3根弧杆改成双弧杆并焊，尺寸大小不变，规格为60.0 mm×30.0 mm(长×宽)，厚度为2.5 mm(图13).

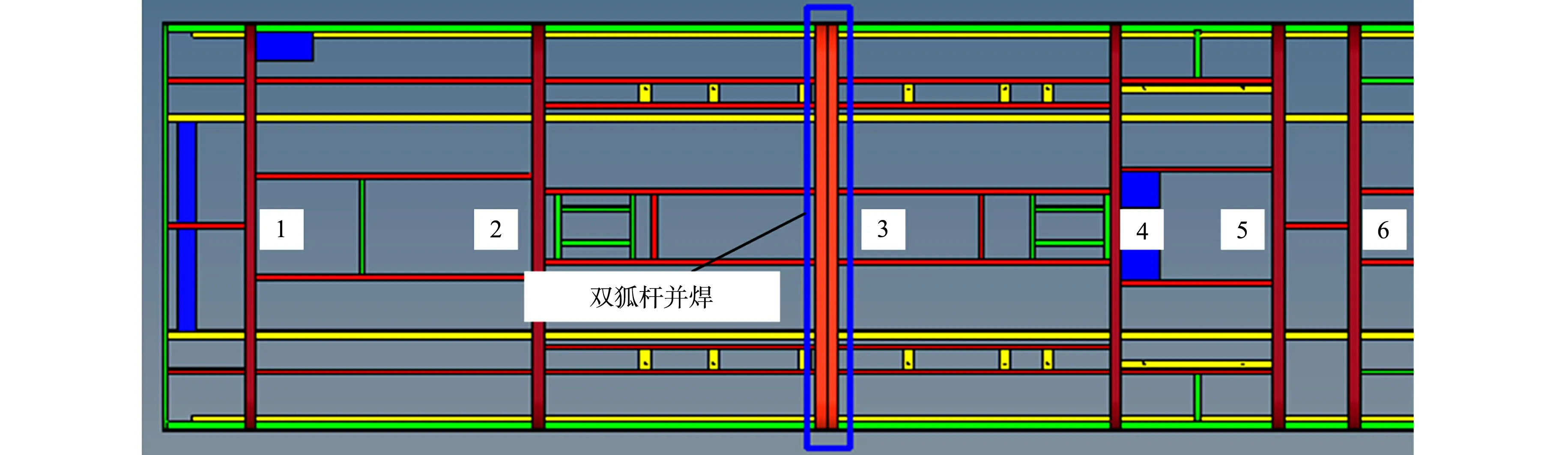
图13 顶盖结构(改进措施1)Fig.13 Top cover structure (improvement measure 1)

2) 改进措施2.通过更改弧杆扣板结构，增强顶盖弧杆扣板与纵边梁的接触刚度(图14).

(a) 更改前弧杆扣板 (b) 更改后弧杆扣板图14 顶盖结构(改进措施2)Fig.14 Top cover structure (improvement measure 2)

经上述改进后，对白车身结构模态进行分析，改进前顶盖模态频率为14.4 Hz，采用改进措施1后的顶盖模态频率为17.9 Hz，采用改进措施2后的顶盖模态频率为18.5 Hz，因此，可实现白车身第3阶模态频率与车内空腔第1阶模态频率的隔离.

5 实车验证

将顶盖结构改进措施1应用于客车，并进行匀速工况下车内噪声测试.在驾驶位测试时，主观感受无明显轰鸣声(车速为80 km·h-1).改进前、后车内驾驶位噪声频谱，如图15所示.由图15可知：当改进后驾驶位噪声频率约为14.0 Hz时，驾驶位噪声声压级峰值较改进前有明显降低，驾驶位噪声声压级最大降幅为4.7 dB(A).

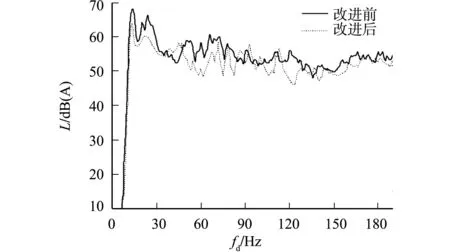
图15 改进前、后驾驶位噪声频谱Fig.15 Spectrum of driving position noise before and after improvement

6 结论

采用实验与仿真方法，对XMQ6182G型客车驾驶位的轰鸣现象进行研究，可得以下4个结论.

1) 通过实车噪声和振动测试可以发现，当客车在30～80 km·h-1匀速行驶时，驾驶位轰鸣声主要来自路面激励.

2) 构建车身结构和车内空腔有限元模型，结构模态频率和声学模态频率仿真值与实验值的误差均小于6.00%，表明建立的有限元模型具有有效性.

3) 模态分析结果表明，白车身第3阶结构模态与车内空腔第1阶声学模态在路面激励下产生声固耦合，引起驾驶位轰鸣声.

4) 顶盖刚度加强后，驾驶位噪声声压级最大降幅为4.7 dB(A)，可提高驾驶位的舒适性.