径向围压条件下的砂粒流失特性试验

陈星欣， 何明高， 房敏安， 郭力群， 尹清锋， 白冰

(1. 华侨大学 土木工程学院， 福建 厦门 361021； 2. 中建交通建设集团有限公司， 北京 100142； 3. 北京交通大学 土木建筑工程学院， 北京 100044)

目前，由渗透破坏引起的砂粒流失给地下工程带来了巨大灾难[1-3].例如，2003年，上海轨道交通4号线浦西联络通道发生渗漏，地下水裹挟砂土颗粒迅速涌入通道内，引起地面和周边建筑物大幅度沉降[4].2012年，桃树坪隧道由于开挖过程中粉、细砂围岩出现严重的涌砂塌方问题，造成重大设计变更，建设工期严重受阻[5].2018年，佛山轨道交通2号线突发透水流砂事故，承压水从渗漏口冲刷流出，造成砂粒迅速流失，导致路面坍陷和重大人员伤亡[6].可见，渗透破坏过程中砂粒的迁移流失常常导致土体强度衰减和失稳变形，进而形成空洞甚至诱发塌陷.

许多学者对砂粒流失的影响因素、演化过程及致灾机理做了许多富有成效的研究工作[7-10].针对黏粒质量分数对砂粒流失机制的影响，张敏江等[11]通过试验指出，弱胶结粉砂中的黏粒质量分数对砂粒流失有阻止作用，黏粒质量分数越高，颗粒之间的胶结强度越大.Bendahmane等[12]通过砂粒流失试验进一步指出，随着黏粒质量分数的降低，砂粒流失速率明显增加.针对砂土级配对砂粒流失特性具有的显著影响，郑刚等[13]通过可视化试验装置对砂粒流失进行的研究指出，临界缝隙宽度与颗粒级配、不均匀系数及颗粒大小有关.田大浪等[14]基于不同细颗粒质量分数的间断级配砂砾石土流失试验指出，细颗粒在土骨架中的填充方式会影响其渗透性.针对土体饱和度对砂粒流失的影响，张冬梅等[15]通过模拟不同饱和度条件下的管线渗流侵蚀过程指出，渗透性和渗流力的大小取决于土体饱和度，饱和土体发生砂粒流失会形成较大的侵蚀空洞.可见，在砂粒流失的内部影响因素上，学者已对黏粒质量分数、颗粒级配、饱和度等做了大量的研究分析，但初始孔隙比对砂粒流失的影响机理还不明确.实际上，随着压实度增大，土体初始孔隙比相应减小，同时，土骨架产生相应变形，颗粒间接触关系会发生明显改变.因此，开展不同在压实系数条件下砂粒流失的研究有重要意义.

针对外部条件对砂粒流失机制的影响，隋旺华等[16]发现裂缝宽度越大，砂粒流失越剧烈，并指出土的平均粒径(d50)小于裂缝宽度的1/10时，容易发生潜蚀甚至涌砂现象.刘成禹等[17]基于砂粒流失试验，发现当破损口为圆形时，砂粒流失引起的上部土体沉降形状可用漏斗表示.另外，水力条件也是砂粒流失的重要影响因素.杨伟峰等[18]通过模型试验发现，在试样顶部施加的侵蚀水头越大，造成的砂粒流失越剧烈.Guo等[19]指出水力梯度和试样高度对砂粒流失形成的空洞形状影响最大.然而，这些研究均未考虑土体受力状态对砂粒流失机制的影响.大量的三轴试验表明，在不同围压条件下，土体物理力学性质大为不同，特别是围压对土体渗透破坏具有显著影响.因此，在试验中考虑围压对砂粒流失的影响是有必要的.

鉴于以上不足之处，本文利用自行研制的三轴砂粒流失试验装置，通过在径向围压条件下的砂粒流失特性试验，研究压实系数、水力梯度和破损口直径对砂粒流失机理和渗透性演化规律的影响.

1 试验装置和试验方法

1.1 试验装置

三轴砂粒流失试验装置由围压控制装置、供水装置、三轴压力室和砂水收集装置4部分组成[20].该装置能对试样同时施加围压和竖向渗流，并能开展试样底部破损处发生颗粒迁移流失及渗透性演化过程的试验研究.三轴砂粒流失试验装置，如图1所示.

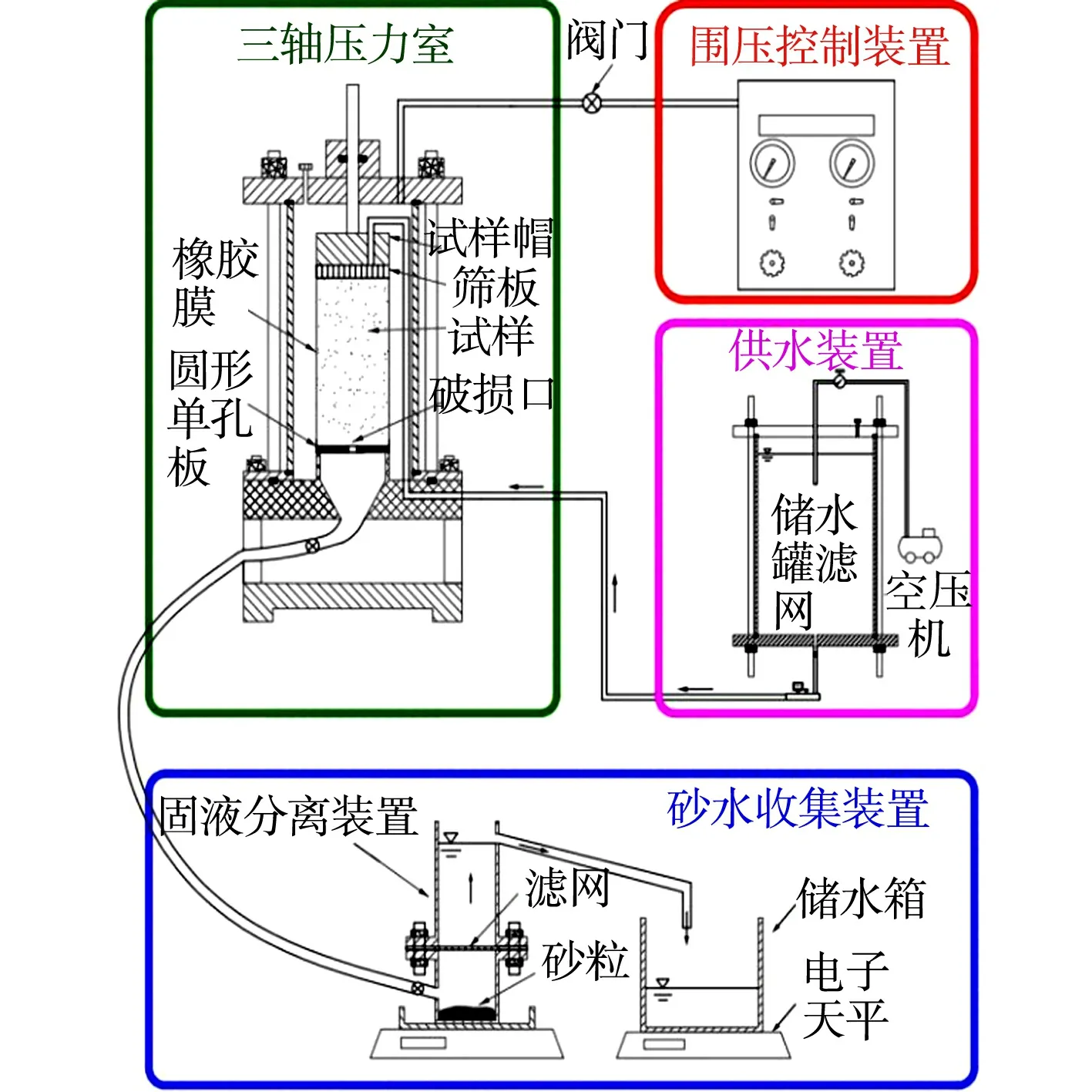
图1 三轴砂粒流失试验装置Fig.1 Triaxial sand loss test equipment

围压控制装置主要用于对试样周边施加径向围压条件.通过调节供水装置中的空压机和精密调压阀，侵蚀水流从密闭储水罐中稳定地流入试样顶部的试样帽，试样帽下表面的多孔有机玻璃筛板能控制水流均匀注入整个试样断面，从而在试样中形成自上而下的均布渗流.同时，在试样底部放置圆形单孔板，用来模拟砂粒从破损口发生流失现象，圆形单孔板正中央的小孔直径需根据试验要求进行设置.另外，三轴压力室主要基于TSZ-3型应变控制式三轴试验仪的三轴压力室改造而成，其压力室内径为103.5 mm，高度为223.0 mm.三轴压力室底座中央掏空成漏斗状，从而满足侵蚀土体顺畅流出、不堵塞管道的要求.

砂水收集装置由固液分离装置、储水箱和电子天平组成.土体内部侵蚀流出的砂水混合物从试样底部圆形单孔板流出，通过内径为15.0 mm的软管流入左侧的固液分离装置.固液分离装置中设置的大孔径滤网可实现固液自动分离，砂粒堆积在分离装置底部，液位在试验过程中始终保持不变，多余液体从顶部溢流口进入右侧的储水箱.结合两个电子天平实时读数即可求得试验过程中砂粒流失量和流水质量.当固液分离装置的天平读数不变时，此时已无砂粒流出，砂粒流失试验结束.

1.2 试验材料

试验选用石英砂作为研究材料，试样的直径为61.8 mm，高度为125.0 mm.根据《土工试验方法标准:GB/T 50123-2019》[21]，对试样进行比质量、相对密度和颗粒分析等常规土工试验.由于试样中存在小于0.075 mm的颗粒，故采用筛分法联合激光粒度仪法进行试样颗粒级配分析，测得试样不均匀系数(Cu)和曲率系数(Cv)分别为8.76和1.72，土颗粒级配良好.试样的干密度(ρd)为1.36 g·cm-3；相对密度(Dr)为44%；平均粒径(d50)为0.122 mm；比质量(Gs)为2.65.试样颗粒级配曲线，如图2所示.图2中：w为小于某一粒径的质量分数；d为砂粒直径.

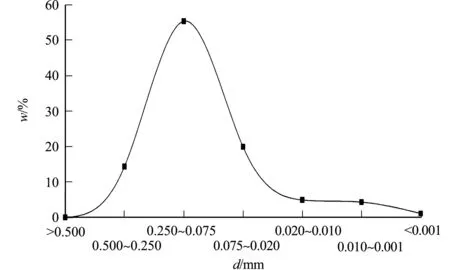
图2 试样颗粒级配曲线Fig.2 Particle gradation curve of sample

1.3 试验方法

为了研究压实系数、水力梯度和破损口直径对砂粒流失机理和渗透性演化规律的影响，开展了3种压实系数(70%，75%，80%)、3种水力梯度(16，24，32)和3种破损口直径(2.0，2.3，2.6 mm)条件下的砂粒流失试验，砂粒流失特性试验总计27个.砂粒流失试验有如下3个步骤.

1) 将三轴仪底座与砂水收集装置相连，往三轴仪底座注入纯水，使得底座空腔和渗漏软管内注满纯水，从而排净空气.

2) 试样分5次装填，按相同次数、相同落锤高度的操作方式分层压实至达到目标密实度，以确保试样整体的均匀性.每层装填完毕时，需保证水面高于该层试样顶部2 mm左右，以确保每层装填的石英砂处于饱和状态，并且每层石英砂捣实完之后应对顶面进行刮毛处理，防止试样出现明显的分层现象.

3) 试样制备完成后，通过围压控制装置施加围压至100 kPa，打开空压机，并调节精密调压阀，使空压机输入储水罐中的气压保持稳定，并将储水罐底部出水端与三轴渗透破坏装置的注水孔连接起来，从而开始砂粒流失试验.

需要说明的是，对试样进行不同水力梯度情况下的砂粒流失试验时，需要通过空压机维持长时间稳定不变的侵蚀水头.试验全过程使用数码相机进行录像，记录两个天平的相关数据.当固液分离装置的天平读数保持不变时，说明已无砂粒流出，此时，砂粒流失试验结束.

2 压实系数对砂粒流失特性的影响

水力梯度为16，破损口直径为2.0，2.3和2.6 mm时，压实系数对砂粒累计流失率的影响曲线，如图3所示.图3中：Rl为砂粒累计流失率，是砂粒累计流失质量与试样初始干质量之比；λ为压实系数；t为时间.

(a) 破损口直径为2.0 mm (b) 破损口直径为2.3 mm (c) 破损口直径为2.6 mm图3 压实系数对砂粒累计流失率的影响曲线Fig.3 Influence curves of compaction coefficient on cumulative sand loss rate

由图3可知：在同一水力梯度和破损口直径条件下，不同压实系数的砂粒累计流失率都可分为无流失阶段、快速流失阶段及稳定流失阶段.以图3(a)中压实系数为70%的情况为例，在0～432 s时间段内，砂粒累计流失率保持为0；在432～1 212 s时间段内，砂粒累计流失率基本上为线性增长，从0增长到49.9%；在1 212～2 082 s时间段内，砂粒累计流失率逐渐趋于稳定，并最终保持在63.4%.因此，在恒定渗流力和径向围压的初始作用阶段，渗流通道尚未扩张，试样保持稳定状态，此时没有砂粒流失；当渗流力大于砂粒间摩擦阻力，试样底部砂粒最先开始流失，试样内部砂粒向破损口位置迁移运动，渗流通道快速扩张，砂粒累计流失率迅速增长；当渗流通道趋于稳定后，砂粒不再流出，砂粒累计流失率保持不变.

由图3(a)可知：在压实系数为70%，75%和80%条件下，砂粒流失启动时间依次递增，分别为432，924，1 134 s，这说明砂粒流失启动时间随压实系数增大而增大；砂粒累计流失率峰值依次递减，分别为63.4%，62.6%和55.6%，这说明砂粒累计流失率随压实系数增大而减小.因此，随着压实系数增大、试样孔隙率减小.颗粒间约束和咬合作用越强，摩擦阻力越大，造成砂粒流失启动时间越长和砂粒累计流失率越小.

由图3(b)，(c)可知：随着压实系数增大，砂粒流失启动时间增大，在较大破损口直径条件下，砂粒流失启动时间随压实系数的增大而增大的幅度有所减小；当破损口直径为2.0 mm时，3种压实系数下的砂粒流失启动时间分别为432，924，1 134 s，最大差值为702 s，当破损口直径为2.3 mm时，3种压实系数下的砂粒流失启动时间分别为516，714，773 s，最大差值减小为257 s，当破损口直径为2.6 mm时，3种压实系数下的砂粒流失启动时间分别为558，564，594 s，最大差值仅为36 s.因此，随着破损口直径增大，试样底部临空面增大，压实系数对砂粒流失启动时间的影响下降；由于压实系数增大的效果不足以抵消破损口直径增大的效果，砂粒累计流失率未明显随压实系数增大而减小，压实系数为75%和80%时的砂粒累计流失率峰值的差异基本可以忽略不计.

当水力梯度为16，破损口直径为2.0，2.3，2.6 mm时，压实系数对累计流水体积的影响曲线，如图4所示.图4中：V为累计流水体积.根据图3数据进一步计算，压实系数对渗透速度的影响曲线，如图5所示.图5中：v为渗透速度.

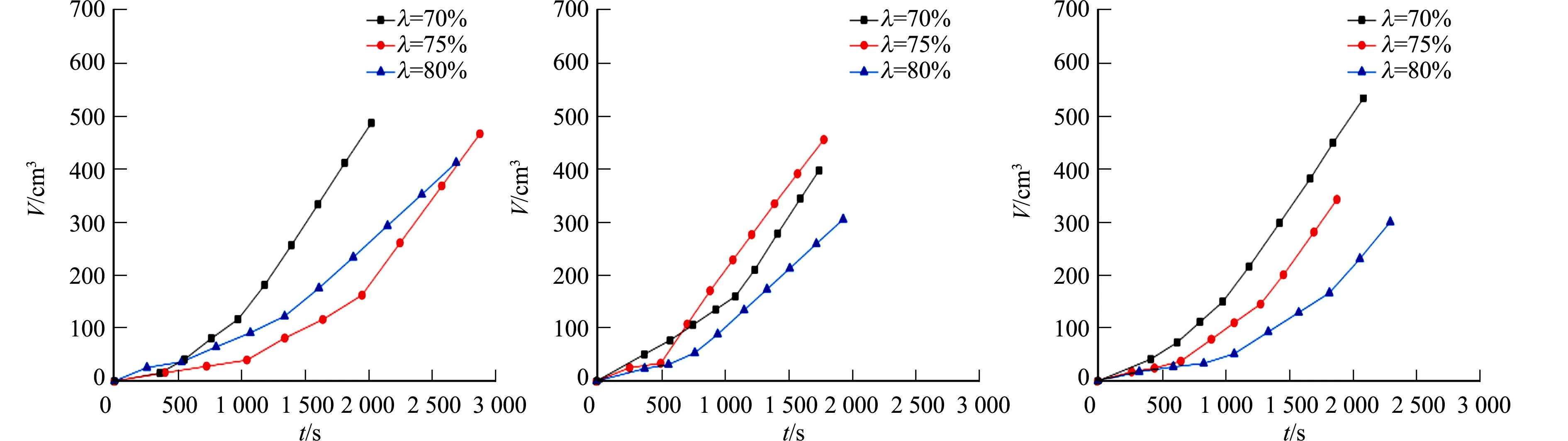
(a) 破损口直径为2.0 mm (b) 破损口直径为2.3 mm (c) 破损口直径为2.6 mm图4 压实系数对累计流水体积的影响曲线Fig.4 Influence curves of compaction coefficient on cumulative flow volume

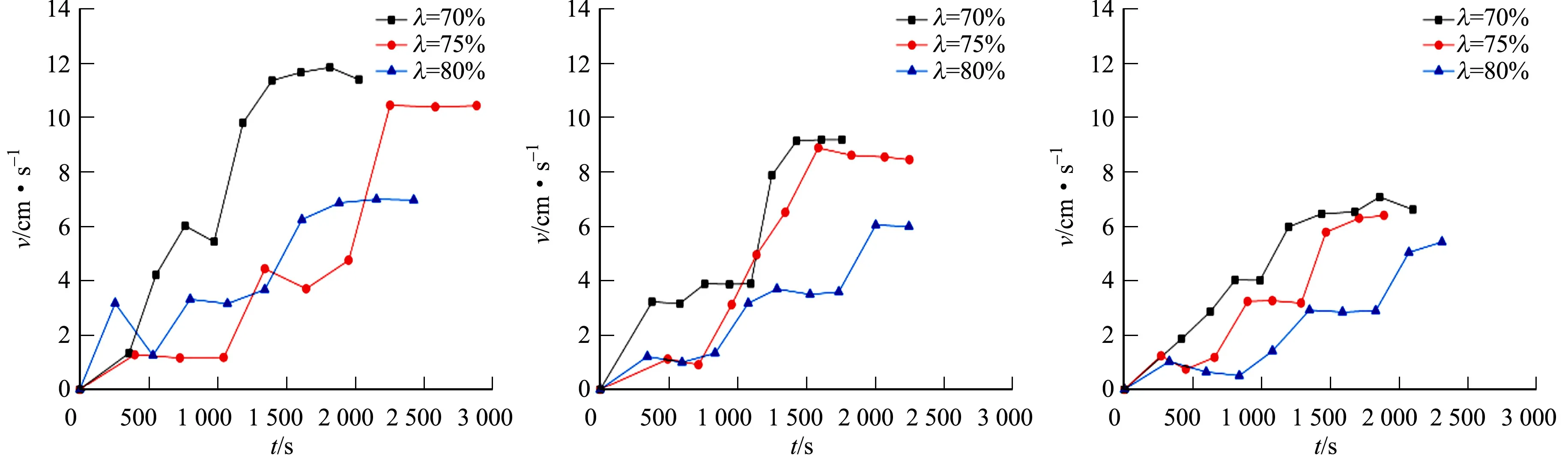
(a) 破损口直径为2.0 mm (b) 破损口直径为2.3 mm (c) 破损口直径为2.6 mm图5 压实系数对渗透速度的影响曲线Fig.5 Influence curves of compaction coefficient on permeability velocity

由图4可知：在同一水力梯度和破损口直径下，高压实系数的累计流水体积可分为缓慢发展阶段和快速发展阶段，而低压实系数的累计流失体积不存在明显的缓慢发展阶段.以图4(a)和图5(a)中压实系数为70%和75%的情况为例，当压实系数为75%时，在0～1 043 s时间段内，累计流水体积缓慢增长，最大渗透速度不超过1.23 cm·s-1，在1 043～2 302 s时间段内，累计流水体积快速增长，并且渗透速度最终稳定在10.45 cm·s-1；当压实系数为70%时，累计流水体积在初始阶段就迅速上升，渗透速度相应地在短时间内大幅提升.因此，随着压实系数增大，试样颗粒排布更加紧密，孔隙率和渗透性能均出现下降.在高压实系数下，由颗粒间连通孔隙构成的渗流通道与试样底部破损口贯通后，累计流水体积并没有快速上升；随着砂粒发生集中流失，试样内部渗流通道加快扩张，渗透速度出现明显上升；但是，在径向围压的挤密作用下，试样孔隙率趋于稳定，渗透速度最终保持不变.

值得注意的是，在压实系数为75%和80%的条件下，3种不同破损口直径的累计流水体积均存在平稳段，而在压实系数为70%条件下的试样则不存在平稳段.这说明在较小水力梯度条件下，高压实系数试样的渗流通道发展过程中存在短暂堵塞现象.以图4(a)中3种不同压实系数的情况为例，当压实系数为70%时，累计流水体积曲线不存在平稳段；当压实系数为75%时，在398～726 s时间段内，累计流水体积曲线呈现平稳段；当压实系数为80%时，累计流水体积曲线在一定时间段内呈现平稳段.结合图5(a)能够明显看出，在累计流水体积存在平稳段的时间内，试样的渗流速度并没有增长，甚至出现下降.因此，试样孔隙率随着压实度增大而减小，细颗粒的迁移流动容易造成高压实系数的渗流通道短暂堵塞，进而导致渗透速度下降，累计流水体积曲线呈现出平稳段.

综上所述，在压实系数为70%条件下，破损口直径大小对累计流水体积的影响基本可以忽略不计，3条累计流水体积曲线的差距并不明显；在压实系数为75%和80%条件下，累计流水体积基本上随破损口直径增大而增大，但随着破损口直径增大，累积流水体积增大幅度减小；虽然不同破损口直径下的累积流水体积差别并不大，但过水断面的面积随着破损口直径增大而增大，造成大破损口直径下渗透速度减小幅度明显.

在破损口直径为2.0 mm的条件下，累计流水体积并未随压实系数的增大而减小，但是，在破损口直径为2.3，2.6 mm的条件下，累计流水体积随压实系数的增大而减小.在图4(a)流水快速发展阶段中，压实系数为80%条件下的累计流水体积曲线介于在另外两种压实系数条件下的累计流水体积曲线之间；在图4(b)，(c)流水体积发展全过程中，累计流水体积基本按照压实系数的大小从低到高依次排列.因此，当水力梯度和破损口直径较小时，渗流通道扩张存在一定随机性；当水力梯度和破损口直径较大时，压实系数对试样渗透性能的影响下降，渗流通道扩张较为容易，累计流水体积在发展全过程均随压实系数增大而减小.

3 水力梯度对砂粒流失特性的影响

当破损口直径为2.3 mm时，在压实系数为70%，75%和80%条件下，水力梯度对砂粒累计流失率的影响曲线，如图6所示.图6中：i为水力梯度.由图6可知：在同一破损口直径和压实系数条件下，不同水力梯度的砂粒累计流失率分为无流失阶段、快速流失阶段及稳定流失阶段，这与压实系数对砂粒累积流失率的影响一致.

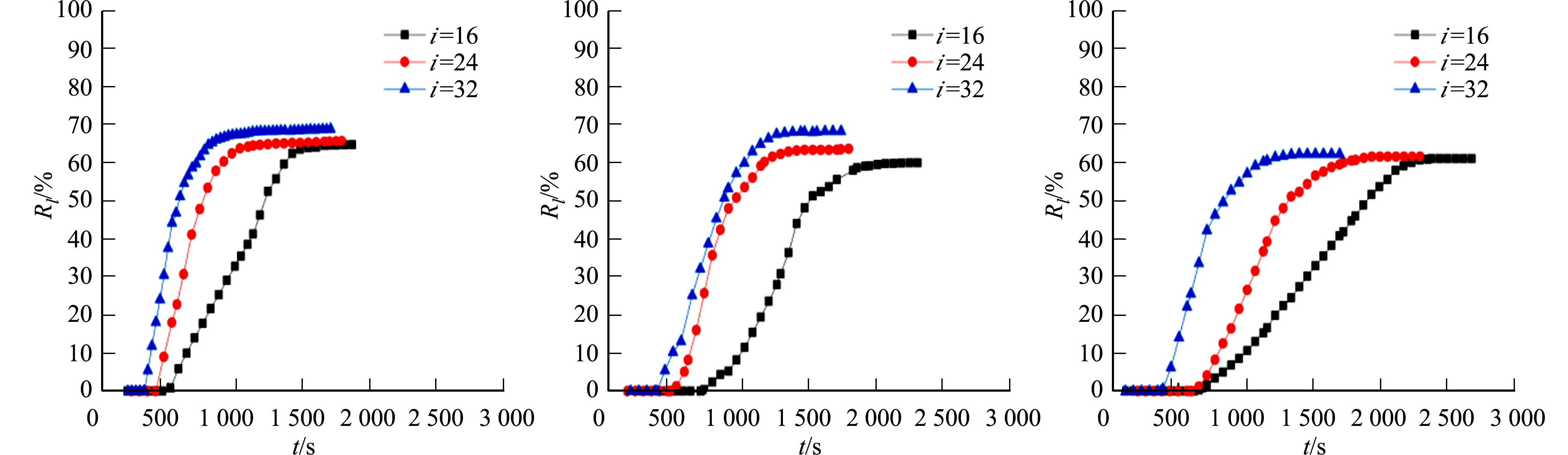
(a) 压实系数为70% (b) 压实系数为75% (c) 压实系数为80%图6 水力梯度对砂粒累计流失率的影响曲线Fig.6 Influence curves of hydraulic gradient on cumulative sand loss rate

由图6(a)可知：在i=16，24，32三种水力梯度条件下，砂粒流失启动时间依次递减，分别为518，468，350 s，这说明砂粒流失启动时间随水力梯度的增大而减小；砂粒累计流失率峰值依次递增，分别为64.6%，65.5%和68.7%，这说明砂粒累计流失率随水力梯度的增大而减小.因此，随着水力梯度增大，侵蚀水头对试样产生的竖向渗流力增大，能有效抵消颗粒间作摩擦阻力，使砂粒流失启动时间越短和砂粒累计流失质量越大.

由图6(b)，(c)可知：随着水力梯度增大，砂粒流失启动时间减小，累计砂粒流失率增大.在高压实系数条件下，水力梯度对砂粒累计流失率的影响基本可以忽略不计.以压实系数为70%为例，在3种水力梯度条件下的砂粒累计流失率分别为64.6%，65.5%和68.7%，最大差值为4.1%；当压实系数为75%时，在3种水力梯度的砂粒累计流失率分别为59.9%，63.5%和68.1%，最大差值为8.2%；当压实系数为80%时，在3种水力梯度条件下的砂粒累计流失率分别为60.9%，61.5%和62.1%，最大差值仅为1.1%.因此，在高压实系数条件下，水力梯度的增大对砂粒流失的影响主要表现为砂粒流失速度的加快.

当破损口直径为2.3 mm时，并且在压实系数为70%，75%和80%条件下，水力梯度对累计流水体积变化的影响曲线，如图7所示.根据图6数据进一步计算，水力梯度对渗透速度变化的影响曲线图，如图8所示.

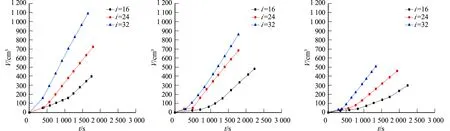
(a) 压实系数为70% (b) 压实系数为75% (c) 压实系数为80%图7 水力梯度对累计流水体积的影响曲线Fig.7 Influence curves of hydraulic gradientin on cumulative flow volume

(a) 压实系数为70% (b) 压实系数为75% (c) 压实系数为80%图8 水力梯度对渗透速度的影响曲线Fig.8 Influence curves of hydraulic gradient on permeability velocity

由图7，8可知：在同一破损口直径和压实系数条件下，累计流水体积和渗透速度基本按照水力梯度的大小从高到低依次排列，这说明累积流水体积和渗透速度随着水力梯度的增大而增大.不同的是，当水力梯度为16时，在不同压实系数条件下的累计流水质体积都可分为缓慢发展阶段和快速发展阶段；当水力梯度为24时，仅在压实系数为75%和80%条件下的累计流水质体积存在缓慢发展阶段，而在压实系数为70%条件下的累积流水体积从初始阶阶段就迅速上升，渗透速度相应地在短时间内大幅提升，并最终趋于稳定；当水力梯度为32时，则仅在压实系数为80%条件下存在缓慢发展阶段.因此，压实系数和水力梯度的相对大小是影响累积流水体积曲线是否存在缓慢发展阶段的重要因素.

当水力梯度为16时，在压实系数为75%和80%条件下的累计流水体积存在平稳段，但是当水力梯度增大到32(图7(b)和图8(b))时，在压实系数75%条件下的累积流水体积并不存在平稳段，其渗透速度在初始阶段没有突然下降而是迅速上升，这说明只要提高水力梯度到一定程度，即使是高压实系数下的试样渗流通道也不会出现短暂堵塞现象.

4 结论

1) 在不同压实系数、水力梯度和破损口直径条件下，砂粒流失均可分为无流失阶段、快速流失阶段及稳定流失阶段.在高压实系数条件下，累计流水体积均可分为缓慢发展阶段与快速发展阶段，并且存在短暂堵塞阶段，而在低压实系数条件下，流水体积基本不存在缓慢发展阶段和短暂堵塞阶段.

2) 砂粒累计流失率基本上随压实系数的增大而减小，随水力梯度的增大而增大.但是，随着破损口直径增大，压实系数对砂粒累计流失率的影响减小.类似的，随着随着压实系数增大，水力梯度对砂粒累计流失率的影响减小.综上所述，破损口直径对砂粒累计流失率的影响最为明显，压实系数次之，水力梯度的影响最小.

3) 累计流水体积基本上随压实系数增大而减小，随水力梯度和破损口直径增大而增大.其中，水力梯度对累计流水体积的变化最为显著，压实系数次之，破损口直径的影响最小.