球杆系统的阻尼自适应抗扰控制
周长新, 聂卓赟, 程前, 何旺祥, 朱恩泽
(华侨大学 信息科学与工程学院, 福建 厦门 361021)
球杆系统是研究经典控制理论和现代控制理论常见的非线性系统平台.目前,学者已对球杆系统进行了较多研究.文献[1]采用基于线性二次型调节器(LQR)与扩张状态观测器(ESO)的控制算法对球杆系统进行研究.文献[2-3]采用比例-积分-微分(PID)和自适应遗传算法相结合的自适应遗传PID方法,设计了球杆系统控制器. 自抗扰控制(ADRC)是一种采用扩张状态观测器、微分跟踪器和带宽参数整定等技术抑制系统扰动的方法.文献[4-5]提出原始的非线性自抗扰控制,并完成了线性化.自抗扰控制器继承了PID控制器的优点,针对工业场景中的应用,提出带宽参数整定方法,将自抗扰控制器的设计从非线性函数参数的经验性选择简化为带宽选择.
自适应控制能够自适应系统的不确定性和外部干扰,从而具有良好的抗扰性能[6].文献[7]提出一种自适应控制器,以实现对外部干扰的渐近抑制.文献[8]提出一种鲁棒自适应算法,以实现不确定非线性系统的自适应跟踪.自适应控制提供了一种提高抗扰性能的新方式,而自抗扰控制器的扰动估计和自适应调节是相容的,自抗扰控制器的扰动估计是一种内环控制器,而模型参考自适应控制(MRAC)又可体现一种外环自适应效果.通过ESO对状态反馈的球杆系统状态进行观察,并估计“总扰动”进行补偿,利用参考模型与自抗扰控制系统之间的状态跟踪误差生成自适应律,通过添加阻尼抑制系统的震荡超调,减少对系统稳定性的影响,从而提升系统的抗扰性能.由于自适应律可作用于跟踪误差,当跟踪误差较小时,自适应抗扰控制系统会自动减小为线性自抗扰控制(LADRC)系统.因此,阻尼自适应抗扰控制可看作自抗扰控制的附加自适应.基于此,本文在自抗扰控制[9-13]的基础上,提出一种阻尼自适应抗扰控制.
1 球杆系统的建模与分析
球杆系统主要由底座、支撑杆、带轮、电机、杠杆臂、小球和导轨等组成[14].球杆系统装置示意图,如图1所示.图1中:d为杠杆臂和带轮的连接处与带轮轮心的距离;θ为带轮转动角度,θ限制于一定范围内;α为导轨偏转角度;L为杠杆臂连接点与导轨转动固定点的距离;Y为小球在导轨上的位移.

图1 球杆系统装置示意图Fig.1 Schematic diagram of ball-beam system device
带增量式码盘的直流伺服电机可以测量电机的转动位置,导轨上的电阻传感器可以实时测量小球的位置.为使小球在导轨上稳定地运行,电机转动带动带轮转动(角度为θ),带轮又带动支撑杆运动,使导轨发生偏转(角度为α),从而使小球在导轨上滚动.
球杆系统装置参数,如表1所示.表1中:g为重力加速度;J为小球的转动惯量;m为小球的质量;R为小球的半径.

表1 球杆系统装置参数Tab.1 Parameters of ball-beam system device
在忽略一些部件的情况下,可通过经典力学理论建立球杆系统的动力学方程,近似得到导轨偏转角度α与带轮转动角度θ之间的关系,即
(1)
通过控制带轮转动角度θ,实现对小球的精确控制.球杆系统控制器的原理是通过控制直流伺服电机,调整带轮转动角度θ,从而对小球进行精确控制.
对球杆系统进行动力学分析,可得小球运动与自身重力加速度、半径、质量、转动惯量、导轨偏转角度及位移之间的关系,即
(2)
由于α的期望值在0附近,故在0附近对α进行线性化,可得

(3)
将式(3)代入式(2),可得
(4)
再将式(1)代入式(4),可得
(5)
系统实际输出量为小球在导轨上的位移Y,输入量为带轮转动角度θ.由表1数据,经计算可得球杆系统的传递函数模型,即
(6)
式(6)中:s为复频域变量.
2 控制系统的设计
阻尼自适应抗扰控制结构由参考模型、ESO和自适应机构等组成,ESO用于观测系统状态和总扰动[8].与LADRC不同,阻尼自适应抗扰控制的前馈控制器和状态反馈控制器可通过自适应机制进行实时调整.这种自适应机制是由ESO状态xo和参考状态xr之间的跟踪误差er推导出来的.阻尼自适应抗扰控制结构,如图2所示.图2中:r为参考输入;u0为自适应机构调整后的控制量;b0为输入增益;u为系统输入(控制量),u=Uin;y为系统输出.

图2 阻尼自适应抗扰控制结构Fig.2 Structure of damping adaptive active disturbance rejection control
2.1 LADRC的设计
(7)
式(7)中:yp为测量输出,yp=Uout;Γ(xp,1,xp,2)为系统的不确定部分;D为外部扰动.
f=(1.853-b0)u+Γ(xp,1,xp,2)+D,f被视为一种依赖于不确定性、控制输入和外部扰动的未知“总扰动”.为了测量“总扰动”,f被建模扩展为状态变量xp,3,可得系统的扩张状态模型,即
(8)
假设f可微分,h有界.为了观测球杆系统的状态和“总扰动”,设计ESO,有
(9)
xp为系统状态,观测误差eo=xp-xo=[eo,1eo,2eo,3]T,其动态系统为
(10)
式(10)中:Bε=[0 0 1]T.

期望传递函数模型选择为
(11)

因此,LADRC控制器的控制量为
(12)
2.2 阻尼自适应抗扰控制的设计
除了LADRC中的干扰估计和补偿外,MRAC可以看作是实现自抗扰能力的另一种方法.这两种方法具有一些相似性和互补性.在参考模型方面,参考模型表示控制方法中设计的控制系统的期望性能,LADRC通过极点配置实现参考模型,但是模型跟踪误差不能产生任何反馈校正;而MRAC可以应用于带有跟踪误差反馈的自抗扰控制中.在状态反馈方面,MRAC常常需要访问被控对象的状态,以实现状态反馈,但由于系统的干扰和不确定性,其应用具有较大的困难;而LADRC最重要的优点之一是ESO可以提供良好的状态估计和干扰补偿.在干扰抑制方面,作为两种不确定性和干扰衰减方法,LADRC的干扰估计和MRAC的自适应调整可在基于ESO的状态反馈控制方案中实现,从而极大地提高控制性能.
针对LADRC,MRAC系统中的震荡超调问题,可在系统中添加减小系统震荡超调的阻尼,阻尼系数ζ>1,这样自适应机构的阻尼能力可以部分地抑制系统的震荡超调.
添加阻尼系数ζ后的期望传递函数模型为
(13)
因此,阻尼自适应抗扰控制的期望控制量为
(14)
式(14)中:F*,K*分别为
(15)
基于以上分析,提出阻尼自适应抗扰控制方案.由于实际的系统状态xp是不可测的,故用xo替代.H(s)的阶数为2,而图2中的观测器阶数为3,因此,为H(s)设置一个额外的状态变量,即xr,3=xo,3,以表示相同状态空间中的跟踪误差.
参考模型在状态空间中可表示为
(16)
er=xr-xo=[er,1er,2er,3]T,er为自适应控制器的调节根据,进而可得到阻尼自适应抗扰控制器的控制量为
u=(Kr+Fxo)/b0,
(17)
其参数为
(18)
式(17),(18)中:K,F分别为状态反馈控制器和前馈控制器的参数;P为设计的正定矩阵,P=PT;ωA为带宽参数,ωA>0,其与能量相关,决定了自适应调节速度;ρ为
(19)
式(19)中:q为量化参数,q>0.
采用标准LADRC设计,有
(20)
由此可得
(21)

3 仿真实验与分析
3.1 仿真分析
为了验证阻尼自适应抗扰控制的效果,将阻尼自适应抗扰控制与LADRC进行比较.加入阶跃响应和阶跃干扰信号,以验证阻尼自适应抗扰控制的响应性能和抗扰性能.当q=0时,阻尼自适应抗扰控制器自动变为LADRC控制器.LADRC和阻尼自适应抗扰控制设置相同的自抗扰控制参数,b0=1.853,ωc=0.75,ωo=8.25,ζ=1.3.阻尼自适应抗扰控制中,q=0.002.
系统的输入信号为阶跃信号,其值为0.25 m,设置系统的响应时间为30 s.当系统运行至15 s时,加入阶跃扰动,扰动值为0.2 m.球杆系统的仿真响应曲线和控制量曲线,如图3所示.由图3可知:阻尼自适应抗扰控制比LADRC的抗扰性能更佳,且震荡超调更小.

(a) 响应曲线 (b) 控制量曲线图3 球杆系统的仿真响应曲线和控制量曲线Fig.3 Simulation response curves and control quantity curves of ball-beam system
3.2 实验分析
为了验证阻尼自适应抗扰控制的实验性能,进行球杆系统控制实验.球杆系统(广东省深圳市固高科技有限公司),如图4所示.该阻尼自适应抗扰控制器在MATLAB/SIMULINK 2015b平台中实现,搭建系统的采样率为100 Hz.实验验证了球杆系统的快速性和稳定性.然后,引入阶跃干扰信号验证阻尼自适应抗扰控制的抗扰性能.

图4 球杆系统Fig.4 Ball-beam system
球杆系统的实验响应曲线和控制量曲线,如图5 所示.由图5可知:相较于LADRC,阻尼自适应抗扰控制能在更短的时间内稳定,且震荡超调更小;小球可以很好地跟踪位置设定值(r=0.25 m);在与仿真实验相同参数的情况下,验证了系统的稳定性和快速性.

(a) 响应曲线 (b) 控制量曲线图5 球杆系统的实验响应曲线和控制量曲线Fig.5 Experimental response curves and contorl quantity curves of ball-beam system
球杆系统控制器参数的自适应曲线,如图6所示.图6中:F1~F3,K均为控制器参数.由图6可以知道:当扰动出现时,小球离开设定位置后能够快速地回到设置位置,阻尼自适应抗扰控制的球杆系统具有较好的抗扰性能.
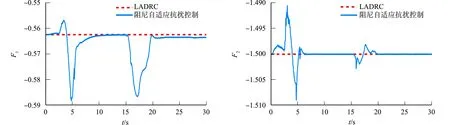
(a) F1 (b) F2

(c) F3 (d) K图6 球杆系统控制器参数的自适应曲线Fig.6 Adaptive curves of ball-beam system controller parameters
由于LADRC的增益是固定的,因此,在不同的运行条件下只能依靠ESO保持良好的抗扰性能,当扰动发生时,由于阻尼自适应抗扰控制的参数调整,参数随之发生变化.通过这种方式,小球的位置稍微向前移动后,能够快速地回到设置位置.相较于LADRC,阻尼自适应抗扰控制的抗扰性能更佳.
4 结束语
球杆系统的阻尼自适应抗扰控制可以减小系统的震荡超调,提升系统的抗扰性能.针对自适应抗扰控制中不稳定非线性系统的震荡问题,通过增加阻尼的方式进行抑制,阻尼自适应抗扰控制可看作自抗扰控制系统的附加阻尼自适应.当状态跟踪误差较小时,阻尼自适应抗扰控制自动减小为LADRC.增加阻尼可以在LADRC的基础上提升系统的稳定性和抗扰性能.仿真和实验结果验证了阻尼自适应抗扰控制的优越性和有效性.

