序列Kriging模型的黑箱约束全局优化方法
师路欢 ,付 虹,李耀辉
(1. 许昌学院 电气与机械工程学院,河南 许昌 461000; 2. 长春工业大学 电气与电子工程学院,吉林 长春 130012)
0 引言
对于仿真优化问题,约束往往是昂贵计算的黑箱函数。这需要对约束函数进行Kriging近似来寻优Kriging预估信息,且加点采样准则的合理使用对产生可行最优解起着关键作用。采用“区域极值定位”准则的约束优化方法[1]将Kriging与偏最小二乘法结合,实现了期望改善的最大化和代理模型的最小化,从而获取可行点。结合EGO和梯度信息,通过初始点变异、多元插值与非插值响应面函数的研究以及模型参数的估计,文献[2]利用广义灰箱约束模型下的优化方法完成寻优。然而,限制全局优化的关键因素是采样点的可行性。针对复杂工程约束问题,文献[3]利用可行域内的全局采样、最大化Kriging的估计方差和局部采样准则三个阶段,提出一种基于Kriging和两目标约束应对策略的代理优化算法。将Kriging与BAT算法相结合的约束优化方法[4]也能减少昂贵估值次数。通过Kriging插值不确定性而改变设计方案的可行性状态,文献[5]提出了基于Kriging和置信区间的序列约束更新方法。也有研究通过新约束加点采样准则在可行域内找到Pareto最优解,完成黑箱约束问题的优化[6]。
上述约束优化只对约束处理提供一种思路,或者只能处理某些特定约束问题,且对初始样本中不存在可行采样点以及对其进行判断和搜索等问题没有进行具体考虑。为此,基于约束改善准则,文献[7]提出一种基于Kriging的约束全局优化方法[7],通过最大最小化约束寻求可行点,并根据Kriging的目标估计与距离因子自适应探索更优可行点。此外,文献[8]使用多初始点优化方法和空间缩减策略提出一种Kriging辅助的约束优化算法,完成可行采样点的搜索和寻优。这两种方法部分解决了Kriging黑箱约束优化问题,但对位于约束边界附近采样点的可行性以及多次搜索不到可行点并没有进行细致探讨,且在平衡全局与局部搜索行为方面需要进一步改进。
为此,本文提出序列Kriging的黑箱约束全局优化方法BCGO-SK(A Black-box Constrained Global Optimization method for the Sequential Kriging model),在初始数据不可行的条件下,完成式(1)寻优。
minf(x),a≤x≤b,x∈Rn,
(1)
s.t.gi(x)≤0,(i=1,…,q),
其中f,g1,…,gq分别表示昂贵且连续的目标函数和约束函数。
1 BCGO-SK方法
1.1Kriging模型
Kriging[9]由回归函数和高斯过程组成,对于设计数据X=[x1,…,xm]T,xi∈Rn及其响应Y=[y1,…,ym]T,yi∈Rq,Kriging模型表达为
(2)

(3)
其中:F和R分别是由已知采样点所组成的回归函数矩阵和相关函数矩阵。
此外,式(2)中的高斯随机项z(x)相当于Kriging插值的估计校正,表达为:
(4)
式(4)中的向量r表示未知点采样点与已知采样点之间误差的相关性,即:
r(x)={R(θ,x,x1),…,R(θ,x,xm)}T。
(5)
为了调节高斯相关函数R(θ,xi,xj)的相关性,通过最小化公式(6)可得到最优参数θ。
min{φ(θ)=-(mlnσ2+ln|R|)/2} 。
(6)
1.2 可行采样点的获取
约束条件可导致初始试验设计无法获取可行点,且无可行采样点的进一步优化将毫无意义。而目标和约束都采用Kriging时,因初始样本数量有限,构建初始Kriging的精确度较低,其近似约束边界与真实边界之间存在较大差异。因此,精确位于近似约束边界上的采样点或许是不可行的。然而,位于近似可行域之内且相对约束边界有轻微偏离的采样点在大多数情况下是可行的。因此,选择式(7)的可行采样策略。
(7)
‖x-xk‖≥ξiterdmax,a≤x≤b,
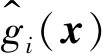
(8)
优化式(7)可得到下一迭代点xnext,并判断其可行性。若可行,则进行更优可行点的探索;否则,将依据其违背约束条件的实际情况,判断是否更新xnext,并将xnext加入数据集X中,直至找到一个可行点。
1.3 更优可行采样点的获取
获取可行采样点后,BCGO-SK方法还需要有效地平衡全局搜索和局部搜索。此外,距离很近的两个采样点会导致Kriging中相关矩阵出现奇异或非正定,甚至构造失败,为此依据已知样本当前Kriging对未知采样点的估计,构造式(9)所示的加点采样准则。
(9)
(10)
其中:参数dmin=min(‖x-x1‖,…,‖x-xm‖)代表未知点x与已知样本X=[x1,…,xm]T之间的最短距离;参数dmax=max{d:x∈X}是X中两点距离的最大值。
1.4 近似约束校正
如果连续多次无法搜索到可行迭代点,就需要找到一个具有最少约束违背的采样点作为伪可行点,并对其轻微扰动来继续找到实际可行点,这个过程称为约束矫正[10]。BCGO-SK的近似矫正主要通过最速下降方式构造如式(11)所示。
(11)
s.t.NTd=e,ATd≤b。
式(11)中的矩阵N和参数e分别表示等式约束函数在矫正点x的梯度和等式约束值取负所构造的矢量,矩阵A和参数b分别表示不等式约束函数在矫正点x的梯度和不等式约束值取负所构造的矢量。规划问题给出当前伪可行采样点x与其距离最近约束边界的方向矢量d。矫正方向确定后,随着违背约束的不断减小,通过试探一系列移动步长,最终获取离矫正点x最近的可行采样点xc。
1.5 算法实现
图1是BCGO-SK的流程图。
对输入和输出参数要求如下。
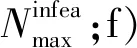
南宋时期的县衙在处理刑事、民事诉讼中,都会涉及对待证人的问题。比如,在已发的命盗案件中,除了追捕罪犯外,还要“勾追取问”那些与罪犯相关的证人、关系人和原告,这些关系者又被称为“干连人”“干系人”“干证人”或“干照人”等。南宋绍兴四年,高宗了解到州县多将无罪人和犯人一样拘禁“动经旬月”,要求“鞫狱干证人,无罪依条限,当日责状先放”,这些事居然都“惊动”了皇帝,可见其严重到什么程度。不过,即便有皇帝的诏令,政府也经常发文“不得长期禁留”干证人,但当时将干证人拘系实为常事,有的竟致干证人“破家失业,或至死亡”,造成了严重的后果。
(2)利用BCGO-SK方法获得的近似最优可行解(xbest,ybest)。算法的实现过程如下:
步骤1 根据拉丁超立方设计[11]获取2(n+1)个初始样本点(n为优化的维度)。对每个初始点xi(i=1,…,m),计算f(xi)和g1(xi),…,gq(xi),得到初始最优化解(xbest,ybest),并设置M:=m。
步骤2 判断并确定初始样本中是否存在可行点。若存在,则直接跳转至步骤4;否则,执行步骤3。
步骤3(阶段1) 执行以下子步骤,直到搜索到一个可行采样点。

步骤3.2 计算出最大距离dmax=max{d:x∈X},其中ξiter根据迭代次数从输入参数中的常数矩阵Θ中获取。
步骤3.3 通过利用PSO算法[12]最小化公式(7)来获得下一个采样点xnext。
步骤3.4 对xnext进行函数昂贵估值,将其增加到样本X中,并设置M:=M+1。
步骤3.5 根据约束函数对,若xnext不可行,则跳回步骤3.1;若可行且xnext小于xbest,则设置xbest:=xnext,ybest:=ynext,并执行步骤4。
步骤4 初始设置连续获取不可行采样点的最大个数Ninfea=0,相应不可行集B=[]。
步骤5(阶段2) 执行以下子流程,找到全局更优可行解,直到满足小于所给定相对容差tol或M≥Nmax。
步骤5.1 通过PSO最小化问题(9)获取下一个迭代点xnext,参数e和D的获取分别通过已知输入条件中给出的权重指数序列值、迭代次数和公式(10)进行相应的选择和计算。
步骤5.2 利用f(x)和g1(x),…,gq(x)对点xnext进行昂贵估值,并设置M:=M+1,更新样本集X。
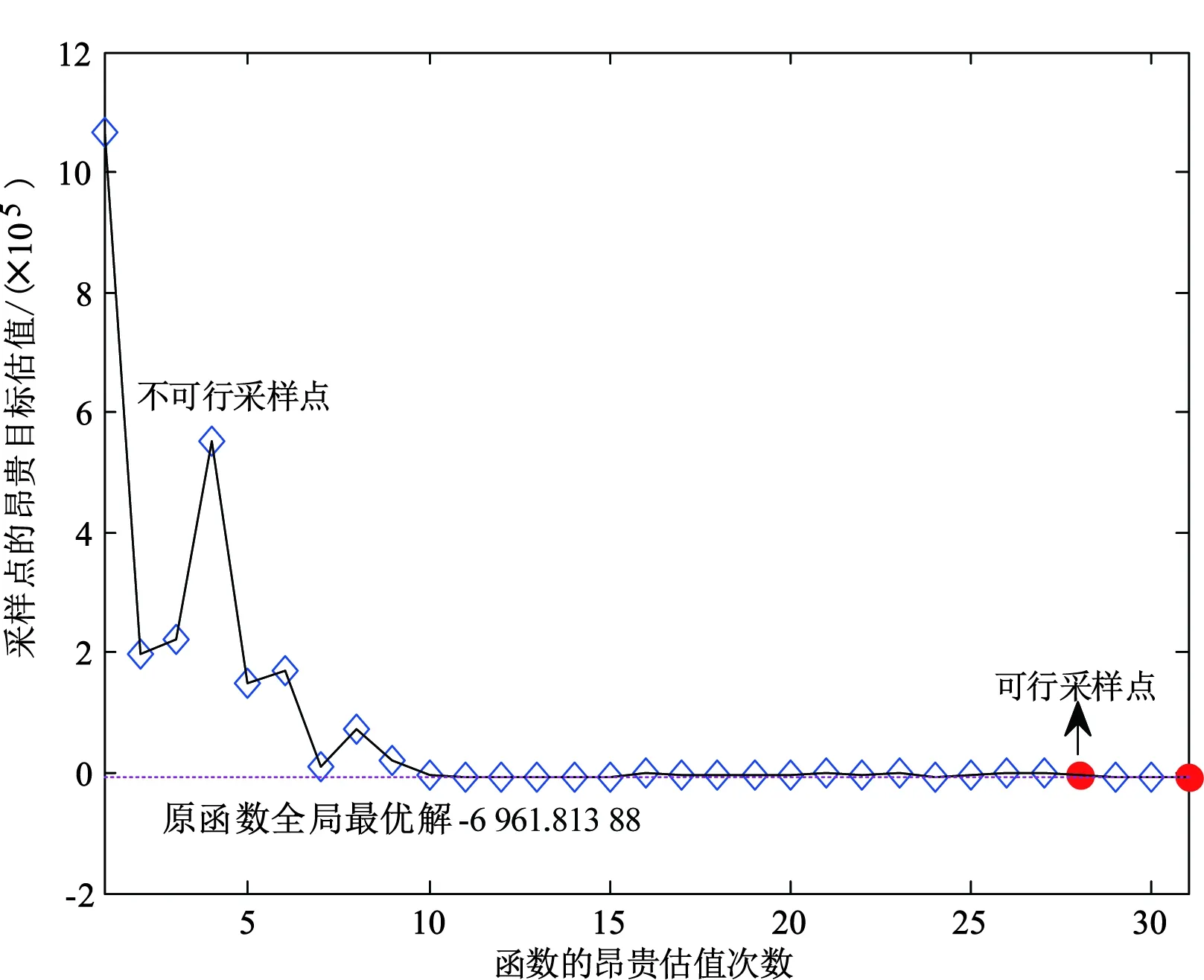
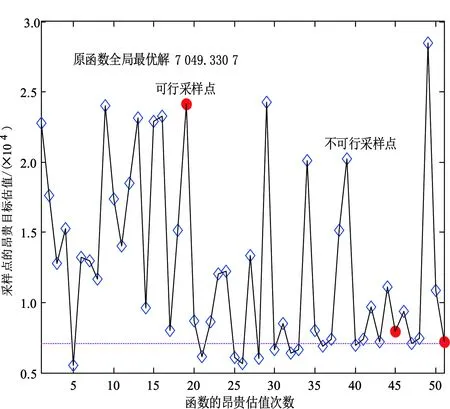
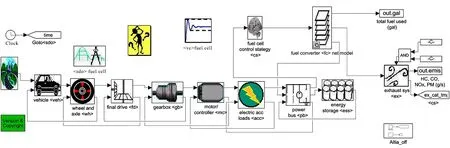
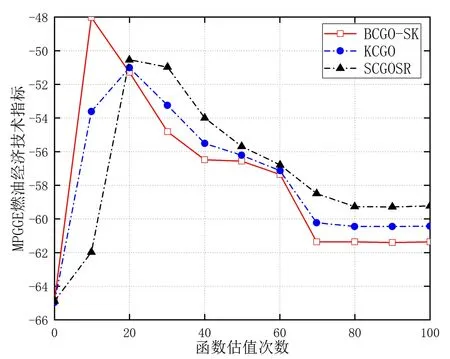
步骤5.3 如果不可行,那么设置Ninfea:=Ninfea+1和Bn+1=[Bn;xnext]。否则,重新设置Ninfea:=0和Bn+1:=[]。若f(xnext) 步骤5.5 在点xc处对f(x)和g1(x),…,gq(x)进行昂贵估值,若xc是可行点,且小于xbest的函数值,则设置xbest:=xc,ybest:=ynext。 步骤5.6 设置M:=M+1,并更新样本集X。 步骤6 返回BCGO-SK算法最终获取的近似可行最优解xbest和ybest。 采用3个不同维度的数值约束函数G6、G4和G10[13]及减速器(SPD)设计实例对BCGO-SK进行测试,通过LHD获取2(n+1)个初始采样点。4个测试函数的基本信息及相关设置如表1所示。 表1 4个测试函数的基本信息及相关设置Tab. 1 Basic information and related settings of four test functions 每个函数在BCGO-SK循环迭代中所获取新采样点的过程如图2—图5所示。图中虚直线表示测试原函数的全局最优解。不可行采样点用菱形进行标记,可行采样点用实心圆作标记。对每个测试函数,在发现第一个初始可行采样点后,通过优化BCGO-SK算法的加点采样准则,都能够快速收敛到一个较好的全局近似最优解。 图2 函数G6的迭代采样过程Fig. 2 Iterative sampling process of function G6 图3 函数G10的迭代采样过程Fig. 3 Iterative sampling process of function G10 图4 函数G4的迭代采样过程Fig. 4 Iterative sampling process of function G4 图5 减速器(SPD)优化设计问题的迭代过程Fig. 5 Iterative process of the optimization design problem of the reducer(SPD) 具体来说,G6、G10和SPD问题都没有获取初始可行点,G4函数在初始采样中也仅仅获取一个可行采样点,特别是具有较窄可行域的G6和G10函数,其获取可行采样点比较困难,这恰好有力证明可行采样准则的存在价值。 在发现可行采样点之后的迭代优化搜索过程中,仅有两个约束可行区间的二维G6函数,能够快速收敛于一个较好的全局最优解;而多维度的G4、G10和SPD问题,由于可行域较多,需经过可行点与不可行点的交替迭代,才收敛于较好的可行最优解。 在绝对误差小于0.05的条件下,所获取全局近似最优解及新增昂贵函数估值次数如表2所示。 表2 4个不同维度测试函数的优化结果Tab. 2 Optimization results of four different dimensional test functions 3个测试函数的优化结果基本满足该误差要求,在较少昂贵估值下,G4的优化结果相当接近真实最优解,而G6、G10和SPD问题也能找到较好的全局近似最优解。为进一步说明BCGO-SK的优越性,基于上述误差条件,将其与KCGO方法[7]和SCGOSR方法[8]的优化结果进行对比,根据10次的测试结果比较,如表3所示。 依据表3,一定程度上能找到合适全局最优解,但需要更多昂贵估值才满足精度要求。而BCGO-SK和KCGO能够在较少昂贵估值条件下获得较高精度的近似最优解,除G10的优化结果以外,BCGO-SK都优于KCGO原因如下: (1)在可行点获取上,BCGO-SK采用最大最小法优化约束Kriging模型,这比采用最大可行概率大于98%的KCGO来说,更易于获取初始可行点。 (3)在多次迭代无法找到可行采样点的情况下,BCGO-SK可通过近似约束校正获取一个离可行采样点最近的伪可行点,以便为进一步寻优提供有利条件,这在KCGO并未使用。 根据图2—图5、表2和表3,得出如下结论:(1)可行采样几乎无法从LHD采样中获得;(2)部分测试问题中,需要一定数量的迭代搜索才能找到可行采样点;(3)对可行区间较大的测试函数(比如G4),需要更多昂贵估值次数。即使如此,未必能得到较好的全局近似最优解;(4)对于G6和G10拥有瘦型可行域的函数,尽管仅找到较少可行采样点,但仅使用较少估值次数就能获取。 表3 BCGO-SK、KCGO和SCGOSR优化结果比较Tab. 3 Comparison of BCGO-SK, KCGO and SCGOSR optimization results 利用BCGO-SK对驱动系统能量控制策略进行优化,使其满足汽车加速性能、爬坡度性能等约束条件下具有更好燃料经济性(如图6所示)。 图6 Advisor平台下燃料电池汽车系统模型图Fig. 6 Model of the fuel cell vehicle system under the advisor platform 该优化问题可以描述为: maxF(x) =Fuel_Economy(X), (12) 并满足以下约束:1)加速度约束如表4;2)爬坡度不小于6.5%的道路上以88.5 km/h速度行驶1200 m;3)循环工况下设定速度与实际速度的最大误差不超过3.2 km/h;4)在初始和最终时刻燃料电池电荷量状态的最大变化ΔSOC≤0.7%。 表4 加速度性能约束情况Tab. 4 Acceleration performance constraints 设计变量X=[cs_charge_pwr,cs_min_pwr,cs_max_pwr,cs_min_off_time]分别表示充电功率、最小功率、最大功率和燃料转换器关闭的最小时间,即:cs_charge_pwr∈[0, 25 000],cs_min_pwr∈[0, 25 000],cs_max_pwr∈[25 000, 50 000],cs_min_off_time∈[50, 1000]。该数据由dv_no_gui调用车辆模型进行仿真计算。 加速度约束通过accel_test获得,爬坡度约束通过grade_test获得,而燃料消耗量、速度误差约束值以及SOC约束值,则可通过test_procedure获得。 由于SOC对燃油经济性的计算影响很大,设定Test_CITY_HWY为综合测试工况。因设计变量变化大,为使其响应面具有一定精度,初始试验设计阶段选择40个采样点。最大迭代次数n=100,最大容许误差为10-4,其他参数的设置参考2.1节。 选择初始参数为经验值X0=[5000, 5000, 45 000, 65]。汽车的燃油经济性MPGGE通过advi_no_gui函数评价,将函数advi_no_gui取负后作为目标函数,使优化设计问题转化为最小化问题。图7为BCGO-SK、KCGO和SCGOSR算法在相同估值次数情况下的优化结果。 初始模型的MPGGE值为64.910,但该模型未能满足3个加速性能约束的要求,且BCGO-SK算法在实验初始阶段的40个采样点均不可行,违反约束程度最小的MPGGE指标为61.078。BCGO-SK需要执行第一阶段以搜索初始可行解,如图7中前30次迭代。 图7 相同估值次数下BCGO-SK、KCGO和SCGOSR算法的优化结果Fig. 7 Optimization results of BCGO-SK, KCGO and SCGOSR for the same number of estimates 之后,BCGO-SK将在已有可行解的基础上找到更优解。对于每一可行解都会进行循环工况测试、加速测试及爬坡度测试,耗时大约3.4 h,总共需140个可行解。可以看出,KCGO和SCGOSR算法在一定程度上都收敛到局部最优解。 综上,本文提出的BCGO-SK具有较好的优化效果,且能在花费较少昂贵仿真次数的情况下获取更优的可行采样点。 基于序列Kriging模型的黑箱约束全局优化算法能够在少量昂贵函数估值的条件下改善优化效率、提高收敛速度,并有效平衡Kriging模型的局部和全局搜索行为,比较适合黑箱约束问题的优化。对于进一步研究,当约束的瘦型可行域仅剩下点和线的情况下,BCGO-SK方法的寻优效果或许不佳,可利用误差带的方法对可行域进行近似逼近处理。此外,以下两种方案或许有助于解决基于Kriging的高维约束优化问题:(1)对Kriging模型的函数结构,特别是相关函数矩阵做行简化处理;(2)将Kriging模型与其他代理模型(比如径向基函数模型)相结合,互补模型之间的不足,完成高维问题的处理。2 算法测试
2.1 测试例子


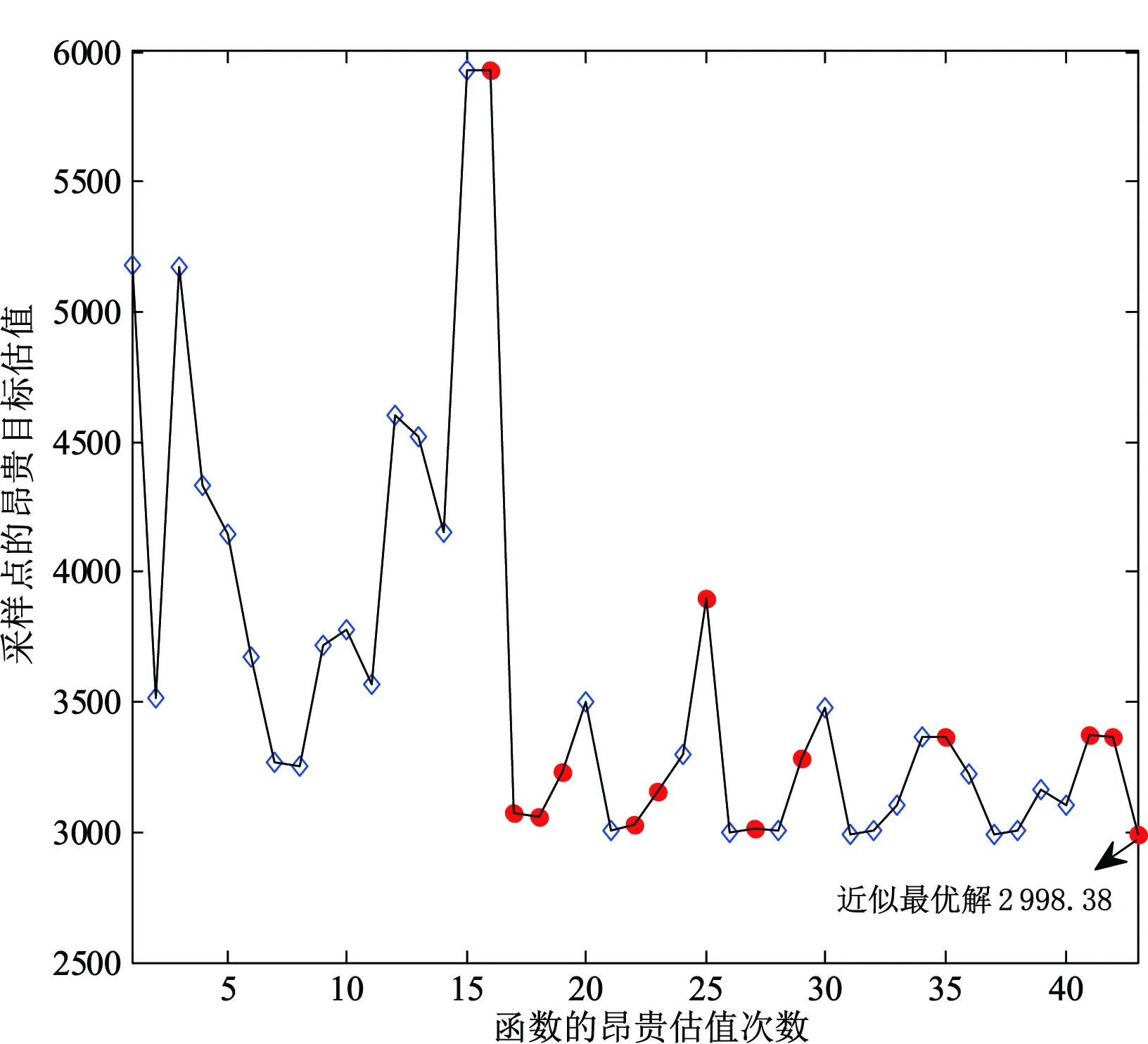

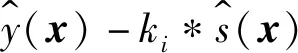

2.2 实例验证

3 结论

