不同压力下CoSb3电子结构和光学性质的第一性原理研究

刘开源，王艳平，赵 卓

(1.鞍山师范学院 物理科学与技术学院, 辽宁 鞍山114007; 2.天津师范大学 物理与材料科学学院, 天津 300387;3.辽宁科技大学 材料与冶金学院, 辽宁 鞍山114051)

0 引言

方钴矿CoSb3是一种非常优秀的热电材料[1]，是最有前途的n型方钴矿化合物。它由比其他方钴矿更丰富、毒性更低的元素组成。CoSb3保留了体热电材料所具有的高ZT特性，是一种具有间接带隙的窄禁带半导体材料,具有小的带隙、高截止载流子迁移率和适度的热电功率[2]。研究表明它具有由常规相跃迁至拓扑相的可能性[3]。此外，CoSb3也是被研究较多的高性能热电材料之一。CoSb3的高热导率严重阻碍了其在热电领域中的应用，但是通过施加压力或应力，使其塞贝克系数、电导率和导热系数发生变化来调节热电材料的性能参数，从而大大提高热电材料的品质因数[4]。随着高压技术的发展，人们发现CoSb3方钴矿化合物更多的优良性质。一般来说，材料的性质在高压下会发生巨大变化。这不仅是减少材料的体积，还会导致晶体结构不成比例的变化。很明显，这些变化将直接影响电子能带结构和相关的性质。施加压力可以强烈地将某些原子从它们平衡的位置上移走，导致新的化学键产生，从而发生相变；也可以使电子能带结构发生显著变化，并且在一定压力下,绝缘体可以变成金属,某些金属也可能变成绝缘体。因此，人们可以通过施加压力改变材料的性质以满足某种技术要求。

CoSb3具有许多优异的性能，具有巨大的科学研究和商业化价值。目前，人们对CoSb3的晶格动力学进行了深入研究。LUTZ等[5]和NOLAS等[6]分别使用红外光谱和拉曼光谱研究了Γ点的晶格动力学。ROTTER等[7]通过非弹性X射线散射实验测量了[001]方向的声子色散。第一性原理[8]计算了声子色散和态密度(DOS)，与实验结果吻合良好。LUTZ等[5]和FELDMAN等[9]通过与第一性原理计算和实验声子频率的拟合，也提出了一些经典的力常数模型。因此为了进一步研究CoSb3的性能，还需通过施加应力、增加压强或者外电场等手段来实现。通常材料的晶格常数会因受应力的影响导致其电子结构发生变化，而相应的电子迁移率也会发生改变，并且材料的声子、拉曼振动模式也会受其影响，因此在材料的光学性质和热力学稳定性方面显示出可调性，而且此方法可有效提高电子器件的性能。

本文基于密度泛函理论的第一性原理，对CoSb3进行不同程度的加压，计算CoSb3晶体的能带结构、声子色散曲线，分析CoSb3晶体的电子结构特性以及拉曼活性和红外活性光谱的振动模式频率的变化，进而认识CoSb3晶体的拉曼光谱和红外光谱性质以及CoSb3晶体结构的稳定性。

1 计算与方法

CoSb3是一种体心立方体，在原始的单元格中有16个原子、4个Co原子和12个Sb原子[3]。采用基于密度泛函理论(DFT)的第一性原理对其进行计算，计算是在Material Studio 2018的CASTEP软件包中完成。该软件是以量子力学为基础，利用赝势替代离子势，用广义梯度近似(GGA)处理电子与电子相互作用的交换相关势，是电子结构计算方面比较优秀的计算软件。选取Sb和Co各原子的价电子组态分别为Sb: 5s25p3，Co: 3p63d74s2。在计算中采用Broyden-Fletcher-Goldfarb-Shenno(BFGS)[10]方法对构建的模型进行原子位置的几何优化，找到CoSb3最稳定时的原子位置，使其获取最稳定的结构并计算出此时的晶格常数。晶格常数为a=b=0.911 5 nm，与实验值0.936 5 nm接近[11]。

在计算过程中,自洽迭代的收敛精度设为5.0×10-6eV/atom，原子间的相互作用力收敛标准为0.1 eV/nm，原子的最大位移收敛标准为5.0×10-5nm，晶体内最大应力收敛标准为0.02 GPa。应用8×8×8的Monkhorst-Pack型k点网格采样对晶胞的不可约布里渊区求和，体系中各原子核内层电子对外层电子的库伦吸引势计算采用模守恒赝势(Norm Conserving Pseudopotential)，所有计算的平面波截断能选取为610 eV。在第一性原理的线性响应法下，计算了不同压力下的CoSb3能带结构、电子态密度、声子色散曲线、拉曼光谱以及红外光谱。

2 结果与讨论

2.1 能带结构和电子态密度

计算CoSb3的能带结构和电子态密度如图1所示。

图1 零压力下的CoSb3能带结构(a)、Sb分态密度(b)、Co分态密度(c)和总态密度(d) Fig. 1 The energy band structure (a) of CoSb3, partial density of states of Sb(b) and Co(c),total density of states (d) at 0 GPa

从图1(a)中可以看出，导带底位于布里渊区的H高对称点处，但价带顶位于布里渊区的Γ高对称点处，导带底和价带顶位于布里渊区的不同高对称点处，因此CoSb3为间接带隙结构，禁带宽度为0.266 eV，与文献[3]的 0.23 eV接近。该结果小于NOALS等[12]的实验值0.55 eV，但是该结果大于采用GGA交换相关势的0.14 eV值[13]。为了更加准确地分析CoSb3的电子结构，计算了Sb原子态密度、Co原子态密度和总态密度，如图1(b)、(c)、(d)所示。通过总态密度和分态密度比较分析可知，CoSb3价带位于-5～0 eV之间，导带位于0～5 eV之间，价带主要由Sb p态电子和Co d态电子构成，而导带则由Sb s态电子和p态电子、Co d态电子决定。

禁带宽度在能带的分析中占据重要位置。禁带宽度直接影响着器件的耐压和耐高温的程度，因此对半导体器件的性能有很大的影响[14]。当禁带宽度很大的时候，电子吸收光子从价带态吸收较大能量跃迁到导带态，这个能量大于热涨落能量，可以继续发挥半导体作用，并且吸收的跃迁能量越大，结构就更难以被击穿，因此被用作制造耐高压耐高温的器件，使其保持高品质的可靠性能。通过对CoSb3施加不同的压力，再次对CoSb3结构进行能带结构的计算，结果如图2所示。

图2 CoSb3在不同压力下的能带结构图(a)5 GPa、(b)10 GPa、(c)15 GPa、(d)20 GPaFig. 2 Energy band structures of CoSb3 at different pressures(a) 5 GPa, (b)10 GPa, (c)15 GPa, (d)20 GPa

由图2可知，在不同的压力下，导带底仍然位于布里渊区H处，价带顶仍然位于布里渊区Γ处，导带底与价带顶依旧位于不同的位置，这表明在加压0～20 GPa的范围内，CoSb3依然是间接带隙半导体材料。在施加压力的过程中价带顶仍然位于布里渊区Γ处，价带顶呈上升趋势，向高能区转移，使其随着施加压力的增加，带隙值也增加。这个结果表明，在对CoSb3施加压力的情况下，它的带隙变宽，不会破坏它的半导体特性以及它的耐高压耐高温特性，在此压力范围内，它依然可以制造稳定、可靠的半导体器件。下文通过声子色散关系进一步阐述CoSb3在高压下结构的稳定性问题。

2.2 声子色散曲线

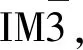
Γ=2Ag+2Eg+4Tg+2Au+2Eu+7Tu，

其中:Tg、Eg、Ag振动模式具有拉曼活性，Au、Eu、Tu振动模式具有红外活性。

计算得到的零压力下的声子色散曲线如图3所示。声子色散曲线可检测晶体结构的稳定性[16]。在图3中横坐标对应布里渊区波矢的路径Γ-H-N-Γ-P-H P-N，纵坐标表示声子所对应的振动频率。从图3中看出，所有振动模式的振动频率均在0 THz以上，由此可以判断CoSb3晶体结构为稳定结构。

图3 零压力下CoSb3晶体的声子色散曲线Fig. 3 Phonon dispersion curve at 0 GPa pressure

声子色散曲线是判断晶体模型稳定性的重要手段。在对声子色散曲线进行计算时，计算出的声子震动模式的频率可以是正值或负值，正值表示稳定的声子振动模式，负值表示不稳定的声子振动模式。如果出现负频率值，即色散曲线中频率小于零，此时该结构可能会出现相变的可能，意味着该结构开始变得不稳定的。当然计算有一定的不可靠性，所以判断时要仔细甄别。如果声学支在高对称点附近有很小的虚频，通过调节相关参数使其负值消失，那么这种结构可以视为稳定结构；如果声子色散曲线值都是正值，那么可以说体系结构是稳定的[17]。为了讨论在不同压力下CoSb3的稳定性，对该结构施加不同压力，计算其声子色散曲线。

从图4可知，在不同的压力下，声子振动模式的频率是正值，这表明在加压0～20 GPa的范围内，CoSb3具有稳定的晶体结构。

图4 CoSb3不同压力下的声子色散曲线(a)5 GPa、(b)10 GPa、(c)15 GPa、(d)20 GPaFig. 4 Phonon dispersion curves of CoSb3 at different pressures

2.3 拉曼光谱和红外光谱分析

拉曼光谱是研究晶格振动和分子基团固有结构特征的一种有效和可行的方法[18]。拉曼光谱是鉴定材料的重要技术，被广泛应用于物理、纳米科学、材料科学等研究领域[19]。下文研究不同压力对CoSb3晶体拉曼光谱的影响。CoSb3共有48种振动模式。如图5所示，通过施加不同程度的压力，CoSb3物质原子之间的距离越来越小，原子间的相互作用增强，其振动模式的频率随着压力增加而增大，即各个振动模式的频率出现蓝移现象。Tg、Eg、Ag振动模式为拉曼活性，其中Tg的振动模式虽然均为活性，但其振动强度与Eg和Ag模式振动强度相比很小。随着施加压力的增大，Tg的振动强度依然很小，因此在图中没有表示出来。Ag和Eg模式振动相对较强，图中最左侧的Eg模式的强度随着施加压力的增加，振动强度减小，但是减少的幅度比较小。最右侧的Eg模式与右侧的Ag模式重叠，随着压力的增加两个振动模式逐渐分开，这两种模式的振动强度相差不多。频率小的Ag振动模式(左侧)随着压力的增加，振动强度变化不大，而右侧的Ag振动模式在压力增加时振动强度变小。

图5 CoSb3晶体的振动模式(a)在不同压力下CoSb3晶体的Eg和Ag振动模式的频率变化曲线；(b)在不同压力下CoSb3振动模式的拉曼光谱Fig. 5 The vibration modes of CoSb3 (a) The frequency curves of Eg and Ag vibration modes under different pressures; (b) Raman spectra of CoSb3 vibration modes under different pressures

红外光谱是分子运动的吸收光谱，其可以提供有关其力学、弹性性质以及与物质结构密切相关的信息[20]。在不同压力下CoSb3红外光谱的计算结果如图6所示。CoSb3的Tu振动模式具有红外活性，Tu有4种振动频率，其对应的红外峰值强度不同。在0压力下CoSb34个谱峰对应频率分别为119.87、245.43、256.41、268.93 cm-1。随着施加压力的增加，峰值位置向频率增加的方向移动，并且其红外光谱的峰值呈现上升趋势，强度明显增加，对应256.41 cm-1处谱峰强度上升得很快。施加应力对红外性质有较大影响，这可以作为分析晶体材料承受压力的一个指标。

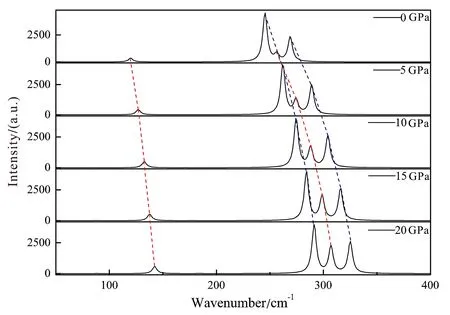
图6 不同压力下CoSb3晶体Tu振动模式的红外光谱Fig. 6 Infrared spectra of Tu mode under different pressures

3 结论

通过计算和分析发现，不同压力对CoSb3晶体结构的稳定性和光学性质有较大影响。随着施加压力的增加，CoSb3的晶格常数和结构体积明显减小，带隙值会随着压力的增加而增加，但是仍为间接带隙半导体材料。在施加不同程度的压力下，会使声子光谱发生变化，随着压力增加，声子光谱频率也会随之增加。在0～20 GPa范围内，CoSb3的结构是稳定的。随着施加压力的增加，Ag和Eg振动模式会产生频率蓝移，并且部分振动模式的拉曼光谱强度会随着施加压力的增加而减小。对应Tu振动模式的红外光谱频率,随着施加压力的增加向着频率大的方向移动，并且峰值会增加。