超精密超声波测距装置设计

王 鹏，张 涛，龚 克，张 昆

(1. 信阳师范学院 物理电子工程学院， 河南 信阳 464000； 2. 中国空空导弹研究院， 河南 洛阳 471009)

0 引言

超声波测距原理简单、技术成熟，已被广泛应用于多种工业、民用非接触测量装置中[1]。其工作原理是测量从换能器到被测目标之间的超声波飞行时间，并利用当前环境下的理论声速反推得到实际距离。因此，超声波飞行时间测量的准确性就直接决定了测距的精度[2]。

目前，测距仪器中使用的实用化超声波换能器主要集中在30～1 000 kHz工作频段。频率越低，超声波的传播效率越好，但测量精度也越低，反之亦然。故实际应用中通常在远距测量装置中使用低频超声波，而在近距测量装置中使用高频超声波[3]。但即使是使用较高频率超声波换能器的产品，其误差也普遍在3 mm左右，且测量精度不稳定，极易受到测量环境，尤其是温度的影响[4]，这一精度虽然能满足绝大多数领域应用，但仍无法达到超精密测量领域的要求。

2016年，仲崇庆等[5]提出了一种基于希尔伯特(Hilbert)变换和互相关的超声波渡越时间算法，在一定程度上减少了高频噪声的影响，但希尔伯特变换解析运算量较大，不适用于嵌入式平台，同时其峰值位置并不明显，只适用于中低频率的换能器应用领域。

在整个超声波测距系统中，影响测距性能的关键因素是飞行时间测量不确定性，此外信噪比恶化和发射盲区也会有一定影响。针对上述因素，从硬件电路和处理算法上着手，在传统设计的基础上进行了大幅度改进，目前已完成多台样机试制并成功用于某精密零件的自动化尺寸检测系统，在使用225 kHz换能器，500 mm典型量程的情况下，测量精度优于0.1 mm，远超现有同类设计[6]，具有很强的工程实用价值。

1 收发电路设计

按照结构不同，在测距系统中可以选择收发一体或收发分体式换能器[7]。前者在收发过程中均使用同一只换能器，体积小、集成度高，但存在一定的发射盲区，即在刚完成超声波发射后的一段时间内受发射余振影响而无法正常接收回波；后者则是采用2只换能器分别用于发射和接收，但需要解决收发物理隔离以防止发射波直接被另一只换能器接收[8]，体积相对较大，成本也较高。

本设计应用背景是某精密零件的自动化无接触尺寸探测，设计目标是测量精度优于0.2 mm，且对换能器体积有严格限制，经多方对比测试，最终选择杭州安布雷拉公司的一款谐振频率为225 kHz收发一体式换能器，其驱动电压Upp最高可达650 V，半功率波束角宽度为8°。

1.1 超声波换能器等效电路分析

超声波换能器有多种类型，如电声型换能器，具体又可分为压电换能器、磁致伸缩换能器、电动式和电磁式换能器；此外还有流体动型换能器,如振腔哨、旋涡哨、旋笛、圆板哨、簧片哨等[9]。目前在电子测量领域中应用最为广泛的超声波换能器为压电换能器，其等效电路如图 1。

图1 压电换能器等效电路Fig. 1 Equivalent circuit of piezoelectric transducer

图1中：R1和C1构成静态支路，R2、L1和C2则构成动态支路。当在换能器两端施加与其谐振频率接近的交流激励时，动态支路形成串联谐振，从而有效地将激励转变为超声波发射出去。同样地，当换能器接收到与谐振频率接近的超声波信号时，动态支路也会发生谐振，并在换能器输出端产生微弱的回波信号。

1.2 高压脉冲激励及收发隔离电路设计

高频超声波在空气中的衰减效应十分明显，为增强回波信号幅度，通常需要利用变压器将发射激励电压Upp升压至数十伏甚至数百伏，但发射电压越高，发射余振影响也越严重，同时功耗也会增加。考虑到实际量程，本设计选择1∶10升压变压器，最终发射电压Upp为65 V。对应电路如图 2所示。

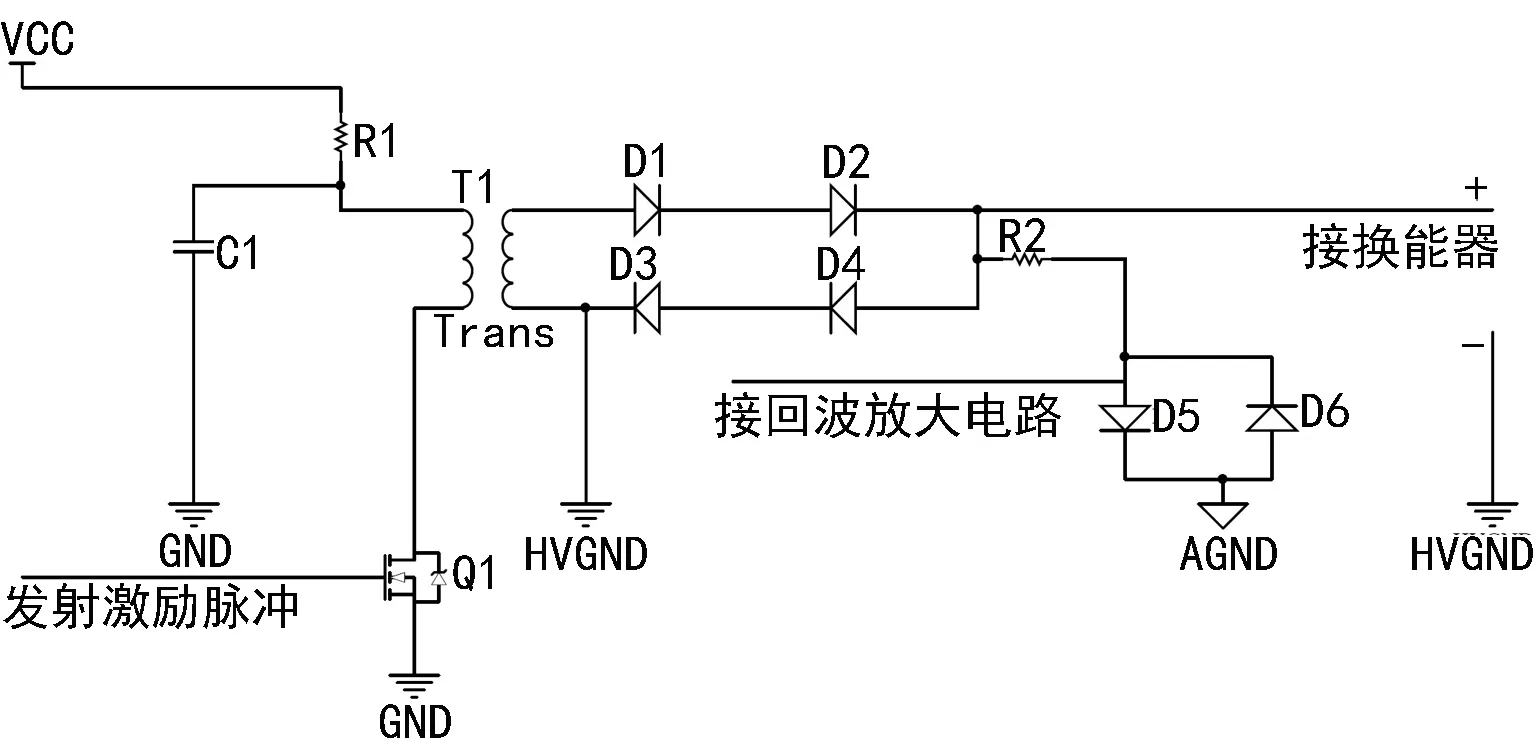
图2 高压脉冲激励电路Fig. 2 High voltage pulse driving circuit

图 2所示电路不仅实现了高压脉冲产生， 还有效地实现了收发隔离，以下说明其工作原理。

当需要控制换能器处于发射状态时，主控制器只需要给出一串3.3/5 V低压脉冲串以控制NMOS管Q1分别处于导通和截止状态，再加上电容C1的存在，使升压变压器的初级线圈电压在UCC为6.5 V和0 V之间随着低压脉冲串的变化而变化，从而可在升压变压器次级线圈得到UPP为65 V的高压脉冲，在高压脉冲的正半周期间二极管D1、D2导通，反之在负半周期间二极管D3、D4导通，最终将高压脉冲能量通过换能器辐射出去。

由于收发一体式换能器回波信号与发射信号共用同一接线端，而回波信号与发射电压相比十分微弱，通常为mV量级，必须对其进行二次放大处理，但如果不进行合理的收发隔离，发射高压直接加在高灵敏度的放大电路上会直接损坏相应的电子元器件。为避免该问题，图 2中增加了D5和D6钳位二极管，可以看到，在换能器发射期间，D5和D6也交替导通，但无论发射电压多高，均可使R2与D5/D6公共端的电压箝位在-0.7～+0.7 V范围内，保护了回波放大电路。而当换能器处于接收状态时，Q1截止，变压器输出电压为0 V，由于回波电压十分微弱，不足以达到二极管的0.7 V开启电压，故D1、D2、D3、D4、D5、D6均处于截止状态，因此换能器的回波电压可以顺利通过R2电阻传递至后级的回波放大电路。

1.3 回波程控放大电路

超声波测距系统依赖于目标反射回波到达换能器产生的微弱电信号实现距离检测，不同的目标特性、不同的探测距离下回波能量变化十分剧烈。为了达到最佳测量精度，应在避免饱和失真的前提下对原始回波信号进行合适的放大，为了适应不同的目标特性和探测距离，必须在换能器回波放大电路中加入可变增益功能[10]。

本设计采用在多级反相比例放大电路中增加数字电位器来实现程控放大功能。为达到更好的放大质量，运放使用了双电源供电，具体电路如图 3所示。

图3 程控放大电路Fig. 3 Programmable amplifying circuit

第1级为固定增益放大，其中C1和R1构成RC高通滤波，R2和C2则实现RC低通滤波。-5 V由专门的负电压LDO芯片TPS 7A3401产生。后2级为程控可变增益放大，数字电位器型号可根据需要的增益范围和信号带宽灵活选择，如AD5260，其最大电阻阻值为200 kΩ，256级档位可调，支持双电源供电，对外通过I2C总线实现档位控制，此时第2、3级放大电路的理论放大范围为1～21倍，再加上RC滤波器和数字电位器对高频信号的衰减，实测该电路在225 kΩ附近的整体放大增益可在20～5 000倍之间灵活调整，足以满足各种环境下的应用需求。

2 发射波形设计

在超声波测距系统中，最典型的发射波形就是如图 4所示的简单方波脉冲串。

为更好地分析收发波形，在图 4激励波形下，图 5给出了利用示波器捕捉的从开始发射到接收到有效回波的完整波形，其中上方为经过变压器升压后到达换能器的发射波形，下方为经过适当放大后的接收波形。

图4 简单方波脉冲串波形Fig. 4 Simple square wave pulse series pattern

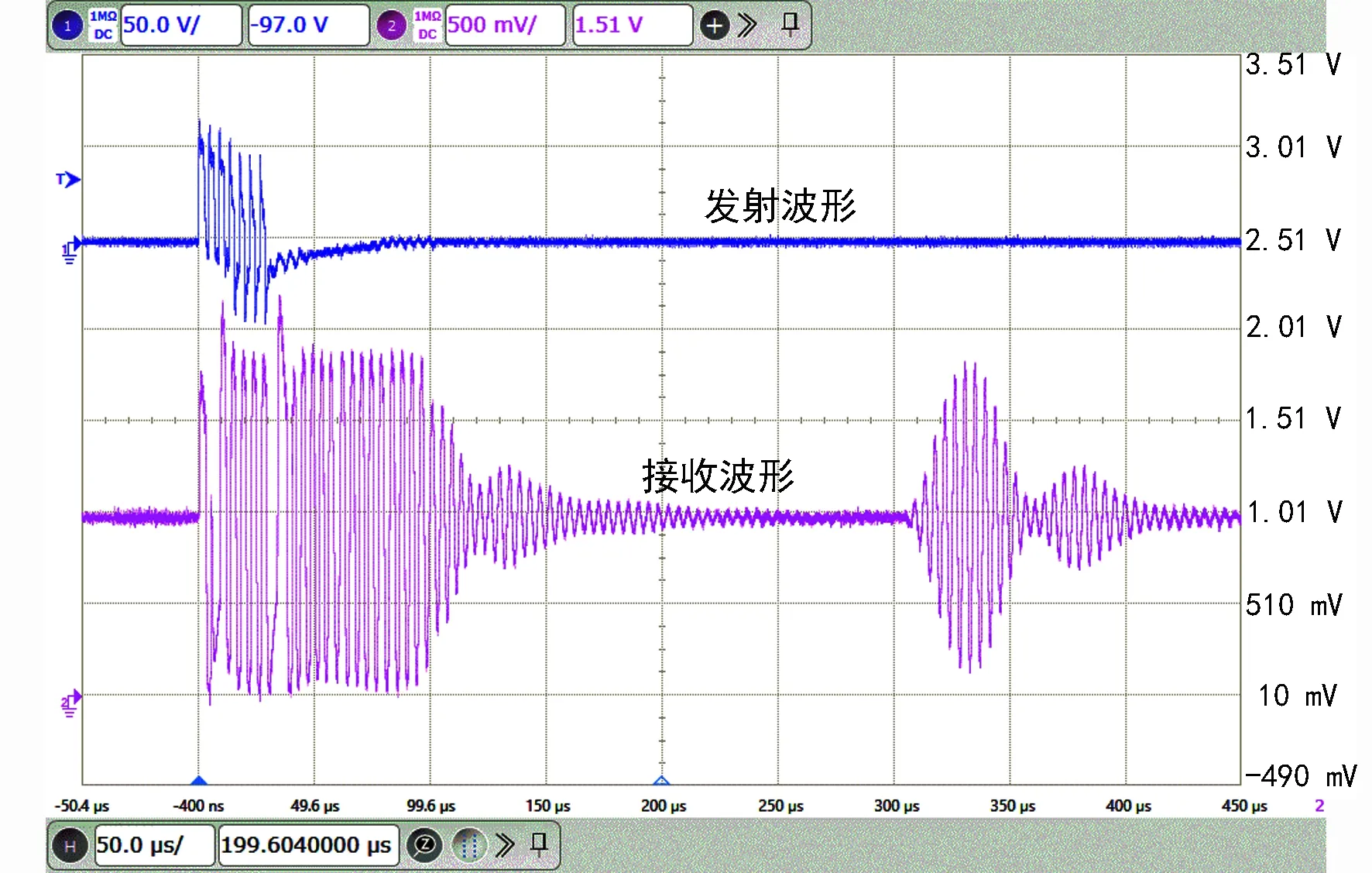
图5 典型收发波形图Fig. 5 Typical transmitting/receiving waveform

可以看出，停止发送脉冲后，换能器两端电压不是立刻降为零，而是有一个衰减振荡过程，即发射余振，在这段时间内，发射电压虽然已明显衰减，但仍远大于换能器的正常回波信号，导致回波放大电路处于饱和放大状态，如果回波信号也出现在这段范围内，就会导致测量盲区现象[11]。

在同一激励波形下，收发一体式换能器的测量盲区是不可避免的，主要影响因素是发射电压的高低和减震结构的好坏，通过适当地调整发射波形，可在一定程度上改善测量盲区。常用的策略是在原发射脉冲串后再发射几个反相脉冲串，两个脉冲串长度的设置则根据实际测试确定最佳比例。例如，先发射7个正向脉冲，再发射2个反相脉冲，从而使发射波形变成如图 6所示式样。其中第2个反相脉冲的作用是产生一个反相激励，从而快速抵消余振波形。

图6 脉冲串后的发射波形Fig. 6 Transmitting waveform when adding inverse pulse series

图 7为改用图 6波形后的整体收发波形，该方案对减轻余振有一定效果，如图 5中150 μs附近的余振在图 7中已基本消失。但是，要达到精密测距的目的，最重要的是如何能找到回波波形中的唯一标定位置，从而能精确地测量出超声波飞行时间。固定/自适应阈值法[12]、时间互相关法[13]、包络重心法[14]等测量算法可以在一定的场合下发挥较好的性能，但都存在缺陷,算法的正常工作依赖于换能器回波特性相对稳定这一前提。研究团队对国内外不同厂家、不同频段的多种换能器进行的高低温测试表明：在较宽的温度范围内，回波幅度及性状(如灵敏度、包络上升下降速度、拖尾长度等关键参数)均会发生明显变化，这恰是许多现有文献所忽略的一个关键因素，同时也意味着前述各种算法对温度变化十分敏感，进而导致实际工程应用中测量误差增加甚至直接失效。

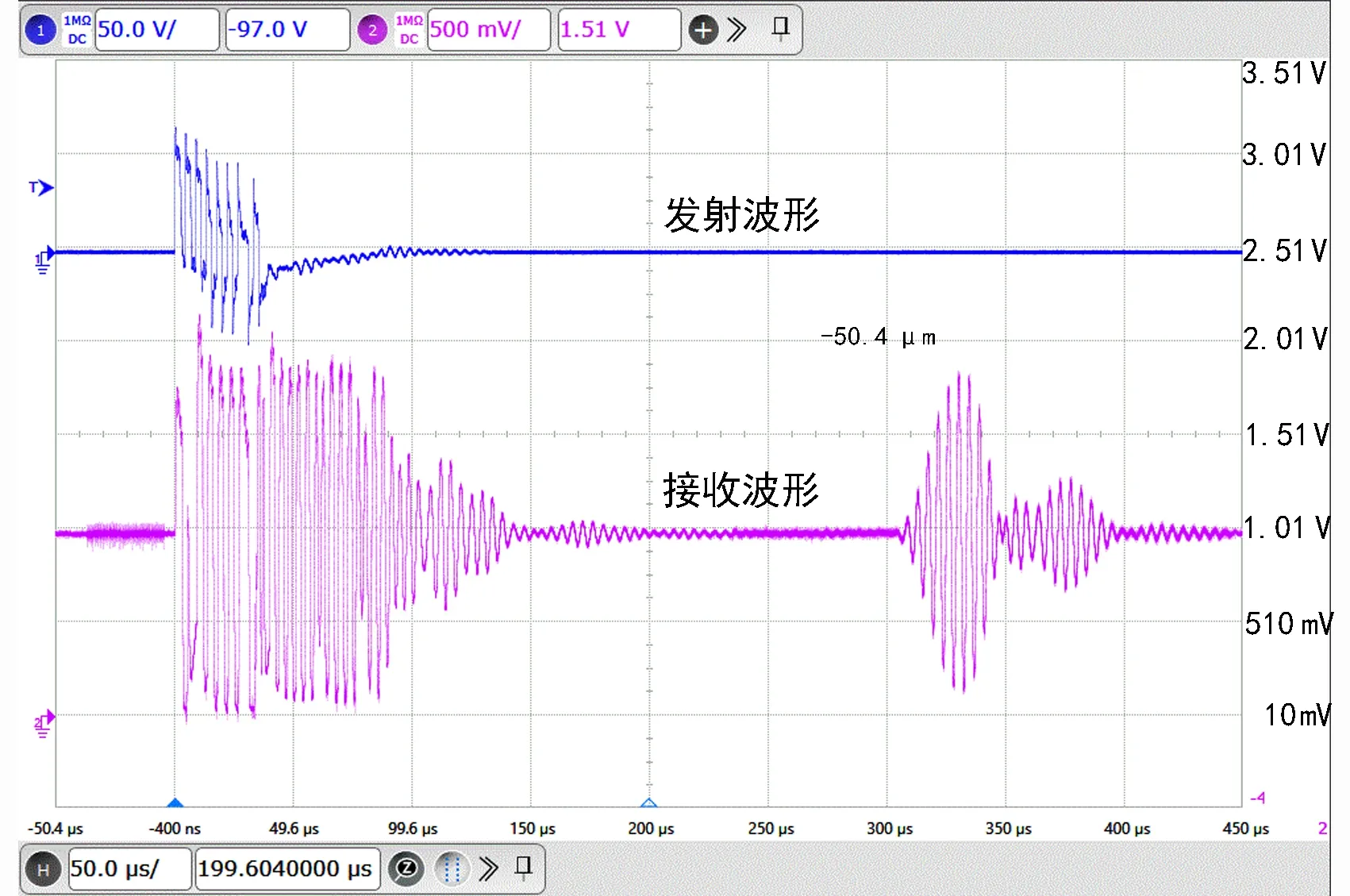
图7 增加反相脉冲串后的整体收发波形Fig. 7 Transmitting/receiving waveform when adding inverse pulse series

为此，本设计对发射波形进行了改进，采用特殊的3段式发射脉冲串作为发射波形。第一个脉冲串为常规脉冲串，脉冲数量可根据实际情况灵活选择，一般为5～10；第二个脉冲串与第一个脉冲串的脉冲数量相同，但相位相反，它不仅减轻了第一个脉冲串响应的拖尾，还使得第二个脉冲串响应的上升速度更为陡峭；第三个脉冲串则用于减少第二个脉冲串的拖尾，其数量实测设置为第一、二脉冲串数量的1/3左右效果最佳。采用该发射脉冲串的整体收发波形如图 8所示。

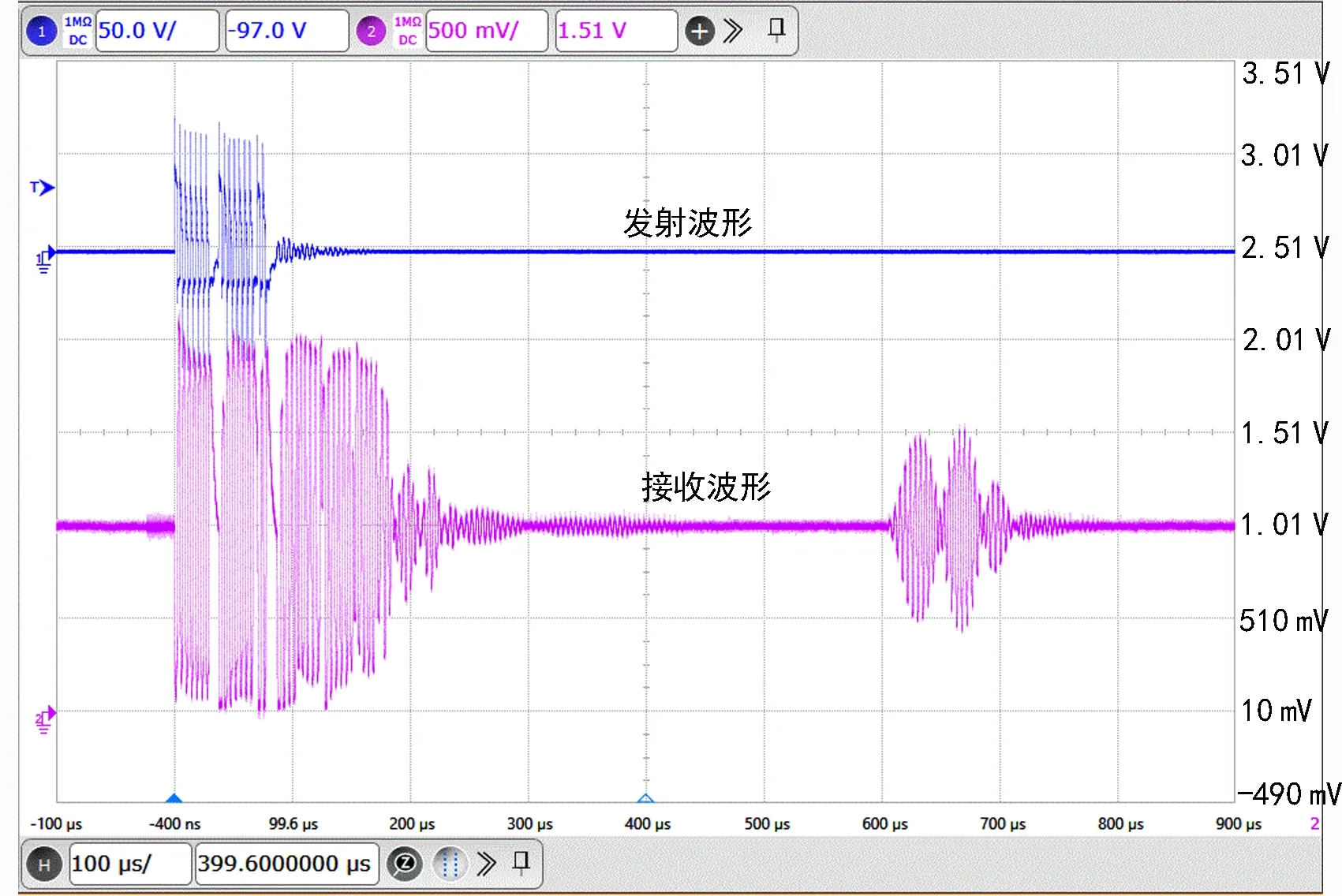
图8 采用3段式脉冲串的整体收发波形Fig. 8 Transmitting/receiving waveform when 3-segment pulse series is utilized

可以看到，此时的换能器回波也可分为三段，为方便分析，图 9给出了回波波形局部放大图。可以看到，第一脉冲串和第二脉冲串的回波响应基本一致，且二者之间形成了一个十分明显的凹陷区域。与已有算法不同，虽然高低温试验表明不同温度下的凹陷程度会发生一定变化，但凹陷极值点的位置却十分稳定。因此，完全可以利用回波包络的第一部分和第二部分之间凹陷极值点的位置来标定超声波飞行时间。

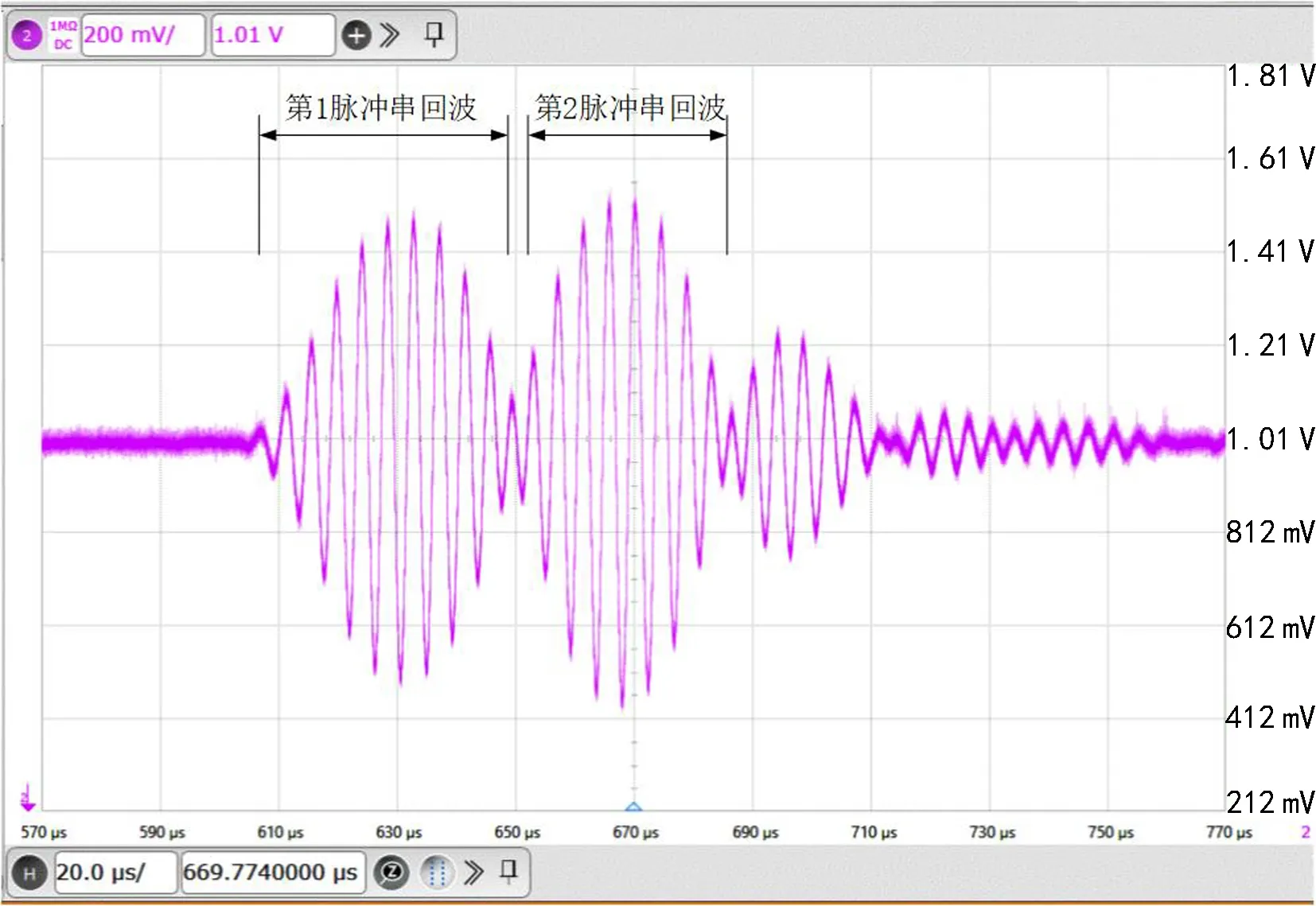
图9 采用3段式脉冲串的回波波形Fig. 9 Receiving waveform when 3-segment pulse series is utilized

3 接收滤波及包络提取

3.1 带通滤波

为提高接收信噪比，在接收端增加滤波器是十分有必要的，常规做法是在图 3电路输出端增加一个带通模拟有源滤波器，如MAX275[15]，然后进入ADC芯片完成数字化。事实上，随着现代微处理器和FPGA性能的显著提高，再结合过采样技术，该滤波完全可在数字域实现，而在ADC前端只需要利用简单的RC滤波器确保符合奈奎斯特采样定理即可。以10 MHz采样率为例，利用Matlab的FDATool工具可以十分方便地设计出带通滤波器(图10)。各参数可以灵活调整，省去了专门的有源滤波器件，进一步降低了系统复杂度和成本。

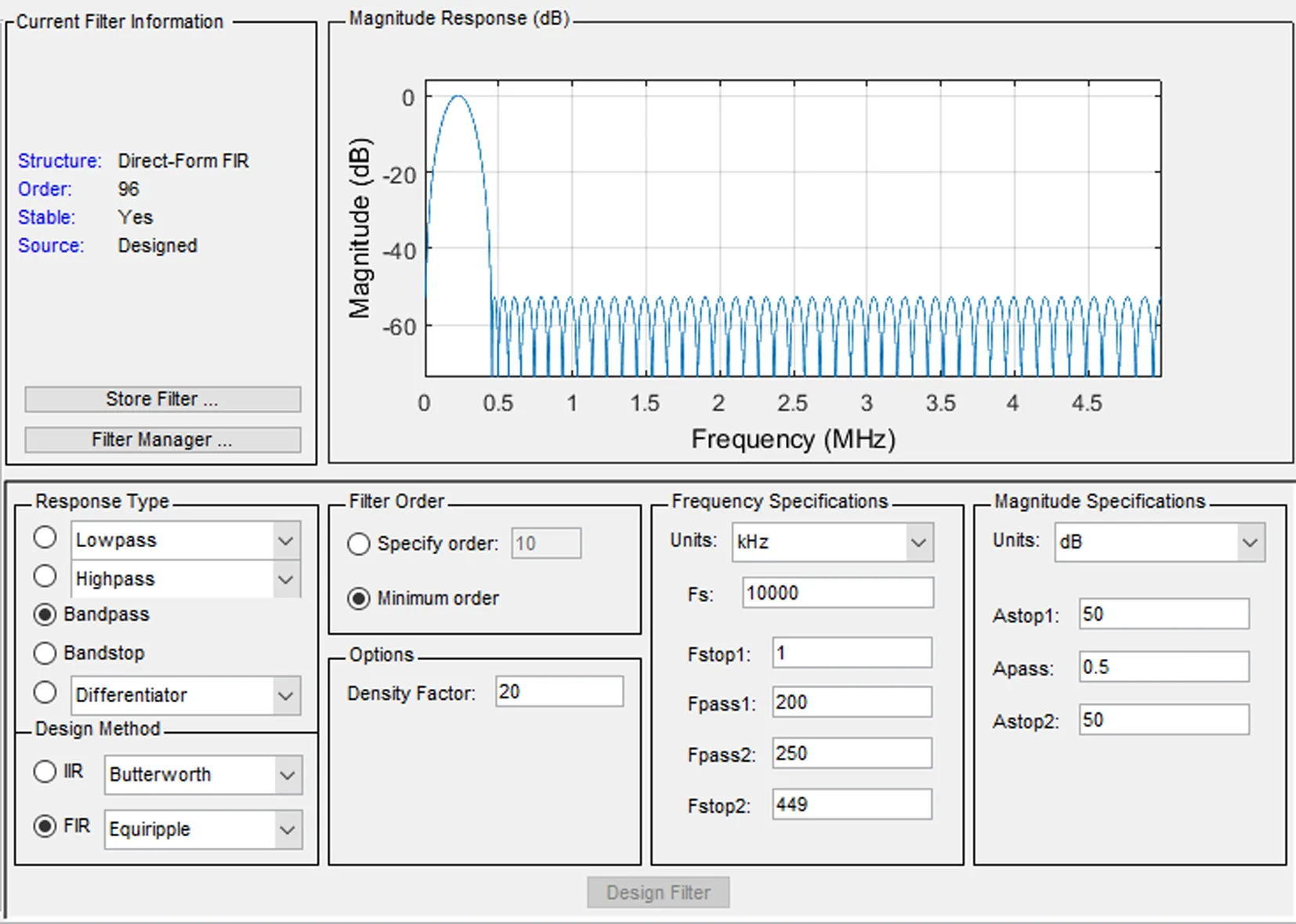
图10 利用FDATool设计FIR带通滤波器Fig. 10 FIR bandpass filter design with FDATool

图 11给出了对ADC采样数据进行带通FIR滤波后的数字化波形，与图 9相比，可以看到波形平滑程度提高，信噪比改善明显。

3.2 包络提取

为了在数字域精确地提取出回波包络，理论上需要对回波数据进行希尔伯特变换后才能得到，但希尔伯特变换的运算量较大，这在许多低功耗嵌入式平台是不适用的。为此，对图 11的回波波形进一步分析，该波形由缓变的包络和快速变化的余弦信号进行抑制载波调制而形成，其中后者的频率基本与发射脉冲的频率相同。因此，提出了一种简化的包络提取算法，具体步骤如下:1)选定测距系统工作主频为Fsys，发射脉冲频率Ftrans=Fsys/Cnt_trans，其中Cnt_trans为发射脉冲计数器的最大计数范围;2)使用3段式发射脉冲串完成换能器发射，得到FIR滤波后的回波数据;3)查找回波波形中第1、2脉冲串回波区域的最大幅度所在位置Pos1和Pos2;4)分别对Pos1、Pos2向左、向右按照Cnt_trans/2为基本步进(即发射频率的半周期)定位至下一个查找位置，在该位置的左右小窗口内寻找最大值/最小值，小窗口的尺度大小可根据实际回波频率波动情况选择合适数值，直至当前找到的最大值/最小值与回波噪底接近或Pos1向右和Pos2向左寻找窗口重叠。该方法的优点是充分利用回波频率相对固定这一特点，极大地降低了运算量，可快速准确找到回波信号的所有极值点;5)按照时间顺序对找到的极值点进行重新排序，利用双线性插值法求得近似包络。

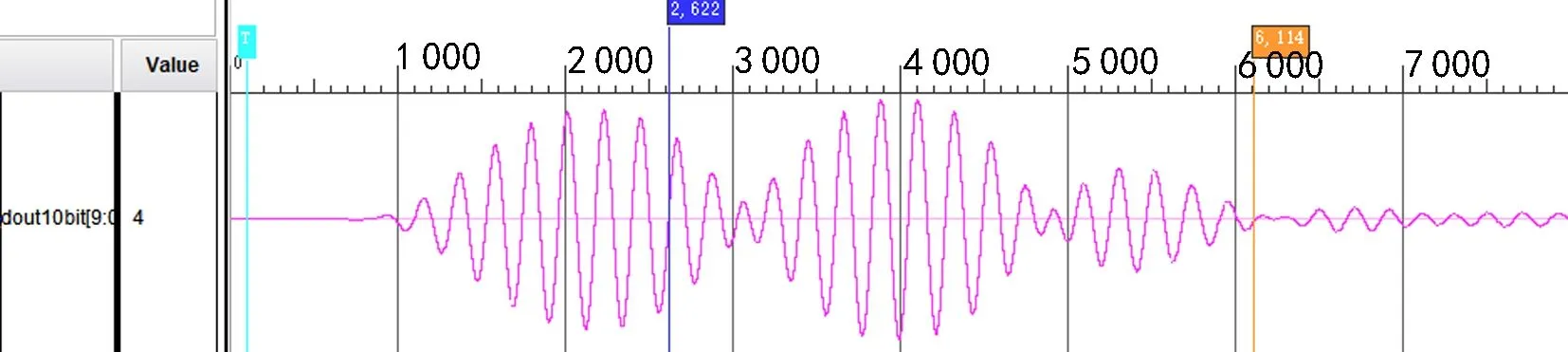
图11 进行FIR滤波后数字化波形Fig. 11 Digitalized waveform after FIR filtered

实测表明，前述算法的复杂度远低于希尔伯特变换求包络法且效果良好，即使是普通的单片机也可以实时快速地完成该运算。图 12给出了按照该算法提取出的近似包络。该近似包络的第1和第2回波区域中间的极小值位置即可作为本次测量的唯一标定位置，并利用高精度计数器得到从开始发射脉冲到该唯一标定位置的传输时间ttrans。

图12 原始回波与近似包络Fig. 12 Original echo and approximate envelope

需要注意的是，受发射电路响应速度和接收电路的滤波延时影响，实际测量得到的传输时间ttrans和真实的超声波飞行时间tflight之间有一个固定偏差tdiff，但tdiff的大小是固定的且与温湿度条件无关，只需事先对某一精确已知距离测量一次即可求得，并不影响最终测量结果的精度。

4 声速解算

在获取准确的超声波飞行时间tflight之后，根据当时的声速Vsonic即可解算出当前目标距离，绝大多数超声波测距装置仅装备了温度传感器，并利用公式(1)计算理论声速，

(1)

其中T为环境温度，单位℃。实际上，影响声速的因素除了温度，还有湿度、气压等，虽然它们的影响因素相对较小，但仍然会对超精密测量造成一定程度的影响，为此，本设计在电路中增加了一片BOSCH公司的集成温湿度气压传感芯片BME280，直接利用I2C总线获取当前环境的温度、湿度、气压，并根据这些环境参数计算对应的水蒸气分压强Pw[16]，利用公式(2)[17]解算出更为精确的理论声速(Vsonic)，并反推出真实的目标距离。

Vsonic=

(2)

其中P为大气压。

5 设计实现

考虑到低功耗、高精度及国产化要求，选择上海安路公司的SoC器件EF2M45LG48B作为主控芯片，该器件基于55 nm低功耗工艺，由中芯国际代工，在片内同时集成了Cortex M3 ARM微控制器和FPGA硬件可编程资源，共包含4 480个触发器和LUT，以及700 kbit块存储器，典型功耗小于0.4 W，且无须片外配置芯片，是一款性价比十分出色的国产高集成度SoC。在该测距系统中，FPGA部分主要用于发射脉冲串产生、AD采样、FIR滤波处理、高精度计时等，ARM部分则主要用于放大增益控制、包络提取、飞行时间解算以及对外信息交互。目前该原型电路板可同时完成4路超声波精密测距，在发射峰值电压为65 V时典型测量距离为30～500 mm，如果需要进行更远距离的测量，可以更换电路板上的开关电源芯片反馈电阻，以提升发射电压，并选择合适的换能器即可。

为进一步提高精度，本设计在每次完整测量周期(目前设置为1 s)内共启动10次测量，其中第1次测量的主要目的是大致定位目标回波位置并评估回波强度，该次测量选择最小增益档以避免回波饱和，并记录回波峰值位置用于设定合适的接收时间窗口，此后的测量仅接收指定时间窗口内的数据以减少虚假回波及干扰信号影响，并选择合适增益以在无失真放大的前提下尽可能增强到达ADC端的信号强度。对后9次测量结果剔除最大值、最小值后做平均处理，即可作为最终的测量结果。

利用标称精度为0.04 mm(0～300 mm)、0.05 mm (300～500 mm)的数显式游标卡尺和该超精密测距装置随机对多组距离进行了对比测量，每个距离均利用自研测距装置连续测量20 s并记录误差最大结果以检验测量稳定性，结果如表 1所示。

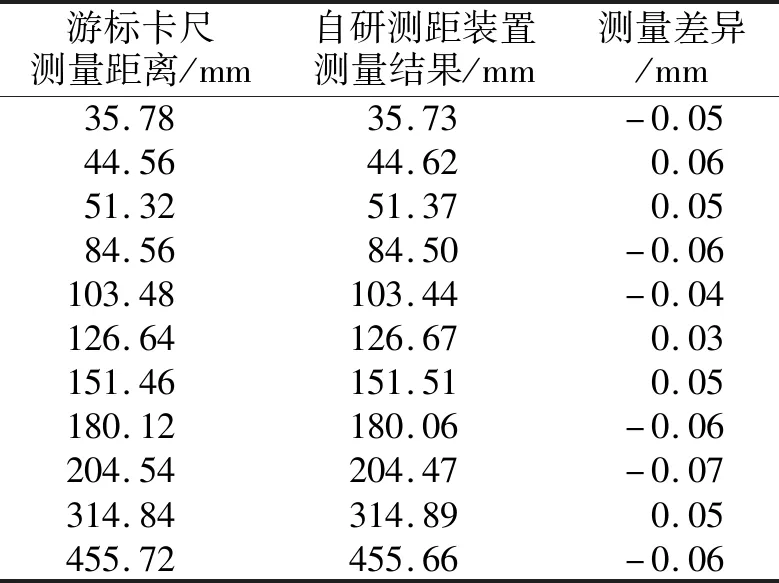
表1 测量距离对比结果Tab. 1 Contrast result of range measuring

可以看到，该超声波测距系统与游标卡尺的测量结果十分吻合，考虑到游标卡尺本身的测量误差，可以认为该测距装置的精度已经与游标卡尺相当，足以完成对目标的超精密非接触测量。

6 结论

按照诸葛晶昌等[18]的研究成果，对典型的超声波测距装置，常规的阈值测量法精度约为1.3 mm，使用小波去噪后可改进至约0. 3 mm；邬文俊等[19]设计的超声波测距装置典型测量误差也在1 mm左右，这些测量指标均是在不考虑换能器回波特性随环境变化这一实际情况下得到的，但实际应用中随着温度的变化，换能器回波特性变化显著，并导致测量精度大幅度下降，这是现有同类设计面临的最大问题。本设计采用了全新的脉冲发射式样，很好地解决了该问题，同时样机实测结果也证实其测量精度不仅优于已有方案，而且不随环境温度变化而变化，目前试制的多台样机均经过了-30～65 ℃高低温环境考核，再加上非接触测量的独特优势，该设计具有工程化推广价值。