考虑负荷与风电跟踪备用的含可再生能源电网调度
贾 磊,段好运,牟光臣
(1.黄河水利职业技术学院,河南 开封 475004;2.商丘技师学院,河南 商丘 476000;3.河南工学院,河南新乡 453003)
0 引言
目前,新能源大规模密集的发展超过了电网的消化能力,同时新能源的波动性和随机性也加重了地区电网调控的压力,常规水电、火电就地平衡的模式和调度方式已不能适应新能源运行控制的需求。因此需要建立全网消纳、调控新能源的机制,尤其是考虑这类新能源机组的备用容量问题。含有风电和负荷的备用动态调度是解决机组出力与备用决策之间量化关系的主要手段[1]。文献[2]提出了基于场景集的含风电电力系统的旋转备用优化。而传统的备用形式主要是以正负旋转备用计及到优化模型中[3],[4]。
在电网新能源调度优化层面上,新能源主要以综合能源系统的形式出现。文献[5]建立了计及用户可响应负荷的区域多能源系统运行优化模型。文献[6]提出一种削峰填谷优化调度模型,通过电转气和燃气轮机协调作用平滑电-气互联综合能源系统净负荷曲线,并兼顾系统运行的经济性。文献[7],[8]引入碳排放,提出了一种电-气互联综合能源系统的联合经济运行模型,以综合能源系统发电能源成本与碳交易成本之和最小为目标函数,综合考虑了天然气网络和电力网络的安全约束。文献[9]探究了含有可再生能源系统的最优能量流的优化调度模型和算法。
目前对于这类调度问题的优化求解方法分为分析法、启发式方法、智能人工算法等[10]。启发式算法在求解这类问题时应用广泛,主要包括对偶半定规划[11]、粒子群(MOPSO)算法[12]、差分进化算法[13]等。这类方法已经较成熟,能够在一般条件下得到最优解。
综上所述,在目前已有研究中,针对负荷与风电场景的动态预测内容较详细,但并未将机组备用水平与预测内容紧密联系,没有突出机组备用受波动性影响的程度。本文考虑动态负荷跟踪备用量化,将负荷、风电的波动误差以概率的形式计及到机组备用水平求解中,从而满足调度的约束要求,得到最佳调度结果。
1 负荷跟踪备用概述
调度机构需要在平衡电力系统功率的同时,确保电力系统能够经受起干扰或者是重大事故。为此,调度机构需要管理一定量的备用,从而能够应对平衡功率之外的电力突发事件。从总体上来说,备用产品在不同电力市场上具有多样化属性。调度机构可以在机组组合或经济调度的同时,确定下一日系统备用的数量,从而保证足够的系统可靠性水平。其中导致电力需要一定量备用的主要因素,包括机组停机等类型的系统扰动、可再生能源和负荷预测误差、可再生能源和负荷的波动性。
另外一种不确定因素是传输过程中的线路损耗。这种不确定因素主要由于网络安全约束导致,考虑到网络的传输极限,需要满足一定的备用条件,使得系统总的功率平衡不受影响。北美电力标准委员会NERC将备用分为以下几类:调频备用、频率响应备用、旋转备用、非旋转备用和附加备用。
本文提出负荷跟踪备用概念,主要是考虑到风电、光伏等波动性电源引起的备用问题。负荷跟踪备用定义为在系统正常运行下,为满足负荷需求不可预测变化以及风电、光伏等波动性能源发电出力不可预测变化而提供的备用。其响应速度在10 min级,持续时间一般在小时级以内。
具体来讲,负荷跟踪备用用于解决负荷以及可再生能源预测误差导致的系统不确定性问题。日前机组组合中的净负荷不确定性,可以依靠负荷跟踪备用解决通过实时调度该备用满足系统功率平衡的要求。负荷跟踪备用需求的维度与调度周期的相关性不高,主要依赖于影响预测误差的关键因素,例如风电功率预测超前时间。负荷跟踪备用主要由调度中心进行人工操作,可以应用于离线机组和在线机组,并且响应速度较快。
2 负荷跟踪备用计算方法
2.1 负荷跟踪备用动态量化模型

式中:n为计算间隔内的量测或预测值,以1 a为计量,n=365×24×4=35 040;m为超前预测时间间隔数,本文考虑超前36 h,在原有时间基础上为37×4=148。
根据上述量测值和预测值计算15 min为间隔的输入矩阵,通过累加的方式可以得到相应时段的最终输入值。
2.1.1 风电和负荷预测值
首先需要获得历史量测数据的基本信息,包括时间间隔等。一般来说,可以通过查阅数据库等手段获得系统负荷以及风电预测数据。这类预测数据一般在1 d内只计算一次,即在调度日前对负荷和功率进行24 h的预测。因此预测的时段比调度时段要领先若干小时。预测时间越超前,预测的误差则越大,体现为标准方差越大。由于目前经济调度是滚动调度模型,需要进行滚动优化,时间需要超前实际调度指令下达时间,因此需要对相应的静态预测值以及动态预测值进行转化,形成与模型输入要求时间尺度相一致的预测水平。预测误差示意图如图1所示。

图1 风电功率预测超前时间与预测误差Fig.1 Wind power forecast lead time and forecast error illustration
①从预测值中减去与静态预测值偏离的均值误差。调整后的24 h静态预测值的精度从小时级转化为分钟级,可以通过插值法实现,最终得到1 d内96点的静态预测值。则预测误差也从量测值中减去预测值得到。
②风电功率预测误差会随着预测时间的提前而增大,通过调整风电预测误差计算时间可以减小这一误差。通过更新后的风电预测误差与相应量测值求和的结果可以得到新的预测值。这一过程应用于所有时间间隔n和所有预测超前时间m情况下,得到n×m的矩阵。负荷预测的过程同该方法。
2.1.2 预测误差分类
动态备用量化基于负荷和风电功率预测误差的非参数分数得到,主要依靠历史数据等。预测误差是从15 min量测值减去点预测值得到的。即:
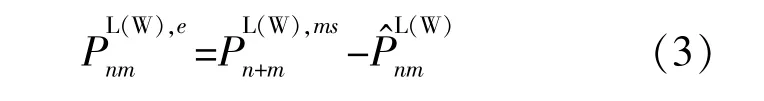
为提高动态备用量化效率,对误差进行分类。
①负荷预测误差。负荷预测误差的分布主要与两个因素相关,预测超前时间和预测发生时间。负荷预测误差与预测超前时间呈正相关,并且与日内误差改变分布相关。这主要是由于负荷具有日变化特性以及可再生能源出力的分布等因素造成的。因此,负荷预测误差分为超前时间类和预测时间类,分别有m=148和d=96种可能,得到m×d的矩阵。最终,根据概率密度函数和累积分布得到误差值。
②风功率预测误差。风功率预测误差也分为两种影响因素,预测超前时间和风电功率预测水平。风电预测时间越超前、风电功率输出误差分布改变量越大,则预测误差越大。因此,风电功率预测误差分为超前时间类和风功率预测水平类,分别有m=148和k=5类,得到m×k的误差矩阵。最终,通过相应的概率密度函数和累积分布函数得到误差值。
2.1.3 负荷跟踪备用需求量化方法

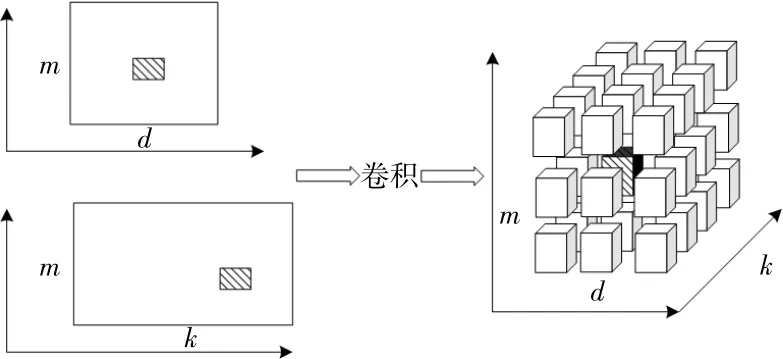
图2 动态备用量化示意图Fig.2 Dynamic reserve quantization schematic
净负荷预测误差的概率密度函数与负荷和风功率预测误差有关。由于负荷和风功率预测误差分为不同类型,因此净负荷预测误差也分为3类,即超前时间m、时间d和风功率预测水平k。预测误差利用卷积进行计算,即:


从上述分析得知,某一时段的备用需求为该时段预测超前时间、预测时间以及预测风功率的函数,并且以动态备用需求的更新频率进行变化,一般为15 min。
2.2 不确定性建模
为描述用电负荷的不确定性,选用高斯分布函数。其表达式如下:

负荷预测值设为函数的均值,标准偏差为2%。另外,分布参数考虑随机分布,利用蒙特卡洛模拟生成不确定参数。
3 含备用量化约束的机组调度模型
本文所提调度模型为含有连续变量和二进制变量的混合整数线性规划。连续变量包括机组出力、传统机组备用容量等;二进制变量包括机组启停状态。约束条件包括等式约束和不等式约束,具体为运行出力约束、爬坡约束、系统功率平衡约束和备用约束等。本文考虑负荷以及风电出力的不确定性,因此与负荷相关的备用具有较高的可靠性。
本文模型是单目标优化,利用粒子群算法进行求解,求解方法不再展开。
3.1 目标函数
确定性机组组合联合经济调度模型的目标函数为最小化运行成本(燃料成本、启停成本和备用成本)、削减移峰填谷成本和弃风成本。


3.2 约束条件

3.3 备用约束条件说明
利用负荷跟踪备用(图3)研究负荷以及风电出力预测值不确定性的影响,约束确保系统上备用和下备用的最大出力在时间k内完成,机组只能够在可调度状态下进行备用操作,约束确保总系统上备用和下备用需求。值得注意的是,快速启动机组可以不提供备用。考虑到这种简化,不需要额外的变量对非备用机组进行建模。
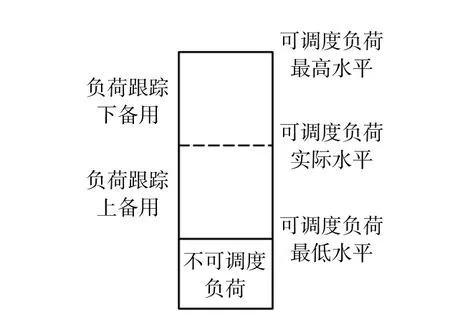
图3 负荷跟踪备用Fig.3 Illustration of load following reserve
本文假设风电出力可以提供下备用容量,并且其成本等于弃风成本,弃风电量可以用于提供实时备用运行。通过相应的人工变量松弛下备用约束,能够满足传统机组对于下备用需求优先性的要求。可调度弃风电量以及风电下备用电量利用风电预测水平进行估计。
4 算例分析
4.1 系统说明
本文选取IEEE30节点系统[14]进行仿真分析,如图4所示,仿真环境为MATLAB2014b。其中机组数据如表1所示。

图4 IEEE30节点系统接线图Fig.4 IEEE30 node scheme
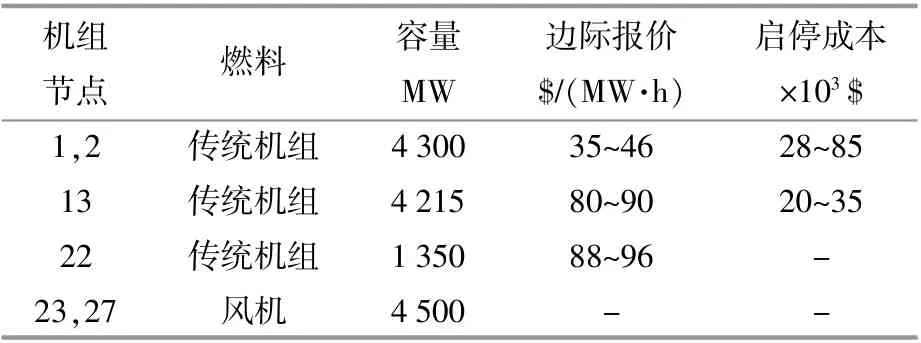
表1 机组数据Table 1 Unit data
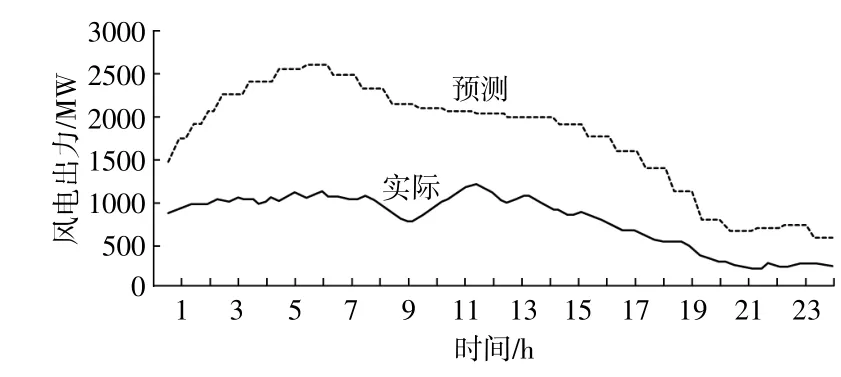
图6 风机出力Fig.6 Output of wind generation
系统负荷、风电功率数据如图5,6所示。传统机组在负荷低谷时的调度可能会导致负荷削减。这是由于机组在负荷增长较快时无法迅速达到负荷变化的爬坡速率。两种模型均为滚动优化。备用需求水平的置信水平为95%,利用动态备用量化方法进行计算。计算频率为15 min,并且基于负荷和风电功率预测误差和更新的备用需求确定调度结果。
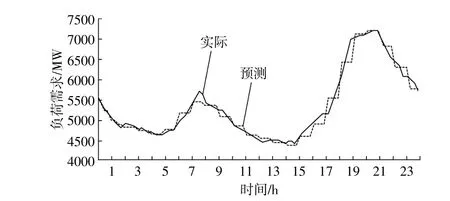
图5 电力负荷需求Fig.5 Electricity demand
在初始条件下,基础场景利用预测模型作为衡量标准。初始预测情景利用负荷以及风电功率预测的水平进行确定性调度,因此调度结果不具有负荷跟踪备用的特性。紧接着,根据不同的备用水平场景进行调度求解。本文置信水平分别为70%,80%,90%和95%。
4.2 算例分析
①机组调度结果
考虑置信水平为95%的情况,仿真得到各机组的总时段内出力,如图7所示。
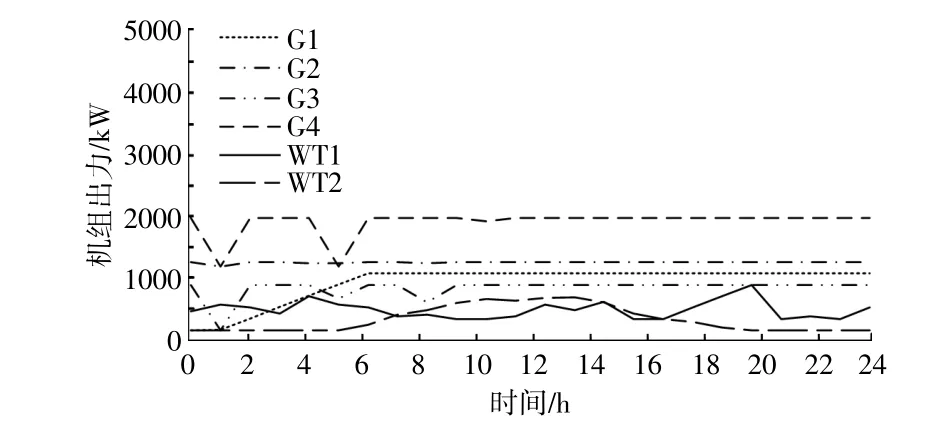
图7 情景1机组电能出力Fig.7 Electricity output for scenario 1
由图7可以看出,G1机组在6时之后出力保持稳定,而两组风机出力均呈现较大波动性。
根据目标函数的计算结果得到的系统成本如表2所示。
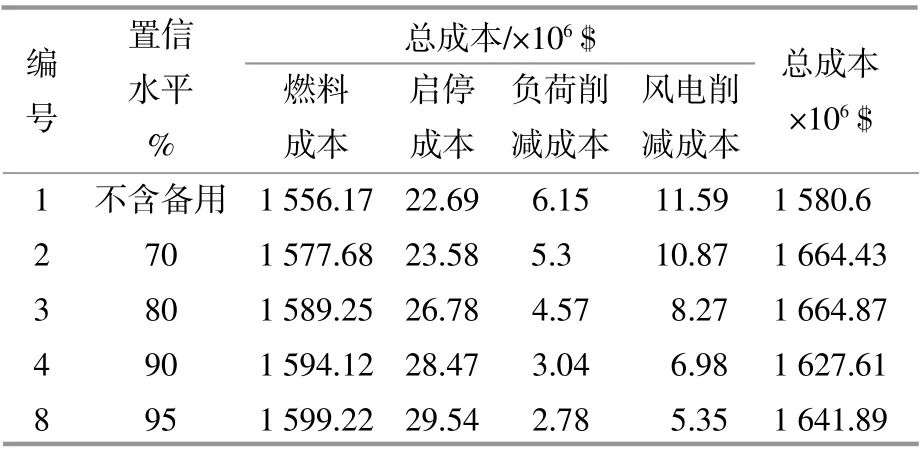
表2 系统成本Table 2 System cost
②备用结果
模型利用负荷以及风功率点预测值对负荷跟踪备用进行调度,在这个过程中,需要利用备用量化方法。得到不同置信水平下的备用功率结果,如图8所示。
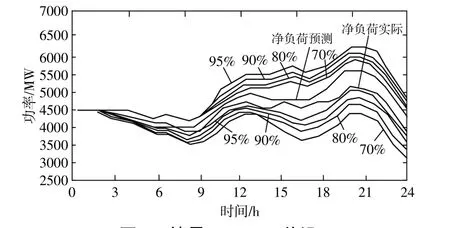
图8 情景2 Pareto前沿Fig.8 Pareto front set in case 2
通过曲线的形状分析可知,备用曲线与负荷需求曲线的走势一致,表明负荷高峰时期备用水平较高。
通过备用水平与计算成本分析可知,对备用水平较高的系统进行调度,由于备用需求的增加,降低了风电削减成本和负荷削减成本,同时也增加了燃料成本和机组启停成本,从而使系统的经济性变差。
5 结论
本文研究了考虑动态备用量化的含可再生能源调度,通过备用量化方法确定了机组的备用水平。根据仿真结果,得到如下结论。
①不同置信水平下的备用需求有所差异,随着备用水平逐渐提升,备用功率也逐渐上升,在整个调度周期内,备用需求始终大于净负荷预测以及净负荷实际需求。
②备用水平与风力发电成本以及弃风功率有着密切联系。备用水平逐渐上升时,风电削减成本逐渐下降,考虑到备用水平主要来自于部分风力发电机组,风电利用率有所上升,从而导致风电弃风成本下降。但这类发电资源的不确定性会导致燃料成本以及启停成本有所上升。
③机组出力和机组备用的关系密切,需要结合电价和能源价格进行分析。

