不同形状的多自由度内置PTO式波浪能转换装置的性能分析

谢惠媚，孟凡泰，徐潜龙，王尚明，谢 彬，李 晔

（1.上海交通大学 船舶海洋与建筑工程学院，上海 200240；2.上海交通大学 海洋工程国家重点实验室多功能船模拖曳水池，上海 200240）

0 引言

波浪能是一种清洁可再生、资源丰富、具有广阔应用前景的新能源。波浪能的全球总量约为2.11 TW[1]。基于不同的工作原理，波浪能转换装置（Wave Energy Converter，WEC）大致可分为振荡水柱式，越浪式和振动浮子式。其中，代表性的原型设备包括Carnegie公司研制的CETO 5，英国Voith Hydro Wavegen公司研制的振荡水柱装置Limpet以及越浪式装置Wave Dragon等[2]～[4]。

根据波能转换系统（Power Take Off，PTO）的放置形式，振动浮子WEC可分为外置PTO式和内置PTO式。外置PTO式WEC的PTO暴露于海水当中，容易受到海水腐蚀。内置PTO式WEC将PTO整合到装置中，使整个系统紧凑，同时不易受到海水腐蚀，在安装和维护上具有极大的便利性。内置PTO式WEC在单一方向的工作效率较低，但可吸收多个方向的能量，如垂荡、横荡、纵荡等，从而提高整体的输出功率。郑明月探究的一种全封闭振荡浮子有两个自由度，可通过最大功率点跟踪实现功率最大化[5]。柴辉采用理论方式验证了三自由度单摆式WEC的可行性[6]。内置PTO式WEC可以从多个方向吸收能量，弥补了PTO内置造成的功率缺陷。

WEC的形状和设计方式会影响其对波浪能的吸收效率。内置PTO式WEC主要利用内部振子与外壳间的相对运动提取能量，如广州能源所研发的“鸭式”、“鹰式”波浪能装置等[7]，[8]。对于外置PTO式WEC，众多学者已经对其形状进行了系统分析，然而关于内置PTO式WEC的相关研究较少[9]～[11]。Lixian Wang提出的圆柱状内置PTO式WEC的最大转换效率约为50%[12]。J Cordonnier提出了一种利用摆锤与主结构体之间的相对运动来吸收波浪能的装置SEAREV1，为了减少抨击、增加稳定性以及降低造价，将初代的扁多面体与棱柱组合改进为凸轮型柱体和类凸轮型柱体[13]。Zhongfei Chen对一种二维船型底和一种锥底圆柱WEC进行了探究[14]，[15]。

本文采用模态分析法研究了一种多自由度内置PTO式WEC的运动特性与功率之间的关系，并从功率、运动幅度、刚度系数、阻尼系数、共振频率和运动轨迹等方面进行了对比分析，探究了外在形状对内置PTO式WEC运动特性以及功率的影响，为后续的WEC外形设计提供了指导思路。

1 内置PTO式WEC模型及数学模型

1.1 模型简介

图1为内置PTO式波浪能装置示意图。

图1 内置PTO式波浪能装置示意图Fig.1 Schematic diagram of the wave energy converter with a built-in PTO

如图1（a）所示，全局坐标系原点位于水平面，其z轴竖直向上。平面入射波沿着全局坐标系x轴正向传播。波浪能装置由4条锚链固定，使其保持半浸没状态，平衡位置位于水平面处。运动锚链被认为是无张紧和无弹的。

如图1（b）所示，波浪能装置主要由外壳、内置球和PTO组成。本研究共分析了3种外壳形状的WEC，即球体、短圆柱和高圆柱，其具体参数见表1。为保证分析结果的准确，这3种形状的WEC具有相同的排水体积。内置球与两组在xz平面内正交的弹簧-阻尼PTO相连。由于整个装置沿xz平面对称，质量均匀分布，在入射波的激励下，装置仅在xz平面内运动，内置球与外壳在垂荡和横荡方向上产生振动，两者不碰撞。内置球与壳体间的相对运动驱动PTO将机械能转化为电能。

表1 内置PTO式波浪能装置的模型参数Table 1 The parameters of the wave energy converter with a built-in PTO

如图1（b）所示：在WEC中，m1和m2分别为外壳和内置球的质量，kg；θ为系统静止时横荡方向PTO与x轴之间的夹角，（°）；k1和k2分别为垂荡和横荡方向PTO中弹簧的刚度系数，N/m；c1和c2分别为垂荡和横荡方向PTO阻尼器的阻尼系数，N·s/m。

1.2 运动方程的建立及优化

1.2.1 运动方程的建立

在波激力和辐射力作用下，波浪能装置的运动可由牛顿第二定律描述：

1.2.3 模态分析

模态分析法是工程振动领域中的一种分析方法，用于研究结构动力特性。通过该方法可计算结构特定频率范围内在内外振源作用下产生的实际振动响应，有利于后续进行装置的结构优化。波浪能装置依靠相对运动产生输出功率，增大相对运动的幅度能有效提高装置的输出功率。固有频率会影响整个装置的动力学特性。本文通过Matlab在运动方程的基础上计算系统4个不同模态的固有频率，通过固有频率分析装置全频域范围的运动表现并研究共振频率下的运动特性。

系统特征值与特征向量满足以下关系：

2 结果与分析

2.1 水动力学结果

根据势流理论，WEC在波浪中受到波浪激励力和辐射力的影响。图2，3分别描述了3种不同形状的WEC在垂荡方向和横荡方向上的附加质量、辐射阻尼和波浪激励力。由图2可知：由于球体WEC和短圆柱WEC的水线面面积相等，所以两者的水动力表现更相近；短圆柱WEC的惯性效应明显，其附加质量高于球体WEC；球体WEC运动时对波面影响更明显，其辐射阻尼高于短圆柱WEC；高圆柱WEC的水线面面积最小，吃水最深，其附加质量和辐射阻尼均最小；球体WEC和短圆柱WEC的波浪激励力大小相近，显著高于高圆柱WEC。由图3可知，在横荡方向上，高圆柱WEC的附加质量、辐射阻尼和波浪激励力均最高。

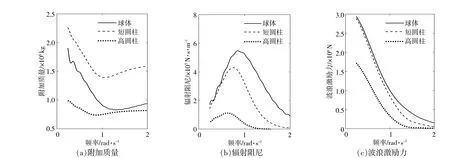
图2 3种不同形状的波浪能装置在垂荡方向上的水动力系数和波浪激励力Fig.2 The hydrodynamic coefficients and wave excitation force of three investigated shapes in the heave direction

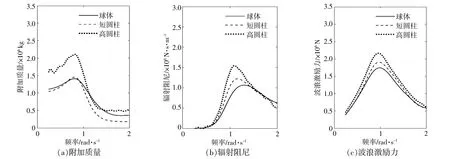
图3 3种不同形状的波浪能装置在横荡方向上的水动力系数和波激力Fig.3 The hydrodynamic coefficients and wave excitation force of three investigated shapes in the surge direction

2.2 运动和输出功率的关系

输出功率是衡量波浪能装置工作能力的重要指标。振荡浮子依靠结构内的相对运动发电，所以WEC的运动幅度可以用浮体相对运动响应幅值算子（Response Amplitude Operator，RAO）和相对速度衡量。本文中，相对RAO为WEC外壳与内置球的振幅差与波高的比，相对速度为WEC外壳与内置球的速度差。

图4，5分别描述了3种形状的波浪能装置在垂荡和横荡方向上的相对RAO和相对速度。

图4 不同形状波浪能装置在垂荡方向的相对RAO和相对速度Fig.4 Relative RAO and relative velocity of wave energy converters of the investigated shapes in the heave direction

从图4可见：在垂荡方向上，短圆柱WEC和球体WEC的相对RAO和相对速度均出现明显的双峰现象，且波峰频率相同，双峰现象主要是由多体多自由度耦合引起的；相对RAO的低频峰值高于高频峰值。低频峰处的大幅度运动会对输出功率峰值有显著影响，而高频峰处的运动幅度虽然不小，但对输出功率贡献很小，仅在输出功率曲线的高频处造成微小波动。

图5中相对RAO曲线的前端横线和相对速度曲线的前端斜线主要是由于外壳和球体横荡方向相对运动幅度差不超过半径的1/100的运动约束造成的，同时，这一约束也限制了WEC的输出功率。在短圆柱WEC和球体WEC的输出功率到达峰值前，其主要受到横荡方向运动约束的影响。在低频处，由于高圆柱WEC在横荡方向相对运动的空间更小，所以受到的约束更明显，在横荡方向上吸收的能量较少，影响了输出功率峰值和能量捕获宽度。在高频处，3种形状WEC的相对RAO曲线和相对速度曲线均有一个微小的波动，但对输出功率的影响很小。结合图4，5可以明显看出，WEC在横荡方向的运动幅值高于垂荡方向，在横荡方向吸收的能量比垂荡方向高，横荡方向的波浪能是能量的主要来源，输出功率曲线的各种特征也主要受横荡方向相对运动的影响。

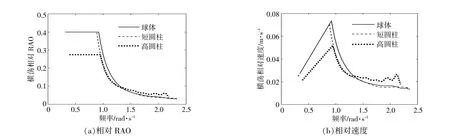
图5 不同形状波浪能装置在横荡方向的相对RAO和相对速度Fig.5 Relative RAO and relative velocity of wave energy converters of the investigated shapes in the surge direction

图6描述了不同形状波浪能装置的输出功率。

图6 不同形状波浪能装置的输出功率对比Fig.6 Power comparison of wave energy converters of different shapes

从图6可以看出：高圆柱WEC具有最高的输出功率峰值，然后依次是短圆柱WEC和球体WEC；输出功率峰值对应的频率由低到高依次为高圆柱、短圆柱和球体，差距不明显。除了输出功率峰值外，能量捕获带宽是衡量WEC工作性能的另一重要指标。能量捕获带宽是指浮子吸收功率超过其最大功率的一半时的频率宽度。从图6还可以看出，球体WEC和短圆柱WEC的能量捕获带宽相似，球体WEC的能量捕获带宽稍微比短圆柱WEC宽，这两种WEC的能量捕获带宽约为高圆柱WEC的两倍。结合功率峰值以及能量捕获带宽可知，短圆柱WEC和球体WEC比高圆柱WEC更适合在实际环境中工作。本文设置的WEC更适合在波浪周期为6～11 s的海域中工作。高圆柱WEC和短圆柱WEC的外壳都是圆柱形，外壳的几何类型相同，但宽高比不同。由高圆柱WEC和短圆柱WEC的输出功率表现可以看出，在排水量等同的情况下，增加WEC的宽高比虽然会降低输出功率峰值，提高峰值频率，但能使能量捕获宽度变宽，更符合实际工作需求。

2.3 分析及原理

图7描述了3种形状WEC由式（10）～（12）优化后得到的刚度系数。从图7可以看出：在垂荡方向上，高圆柱WEC的刚度系数显著高于另外两种WEC，主要原因是，在特征频率相似的情况下，高圆柱WEC在垂荡方向上的附加质量最小；在横荡方向上，3种形状WEC的刚度系数基本一致。3种形状外壳在横荡方向上的固有频率接近0，内置球质量相等，为了使内置球在横荡方向上达到共振，优化结果为PTO系统在横荡方向上的刚度系数几乎相等。同时，由PTO系统在横荡和垂荡方向上的刚度系数与质量之间的关系可知，横荡方向刚度系数与垂荡方向刚度系数呈负相关关系。

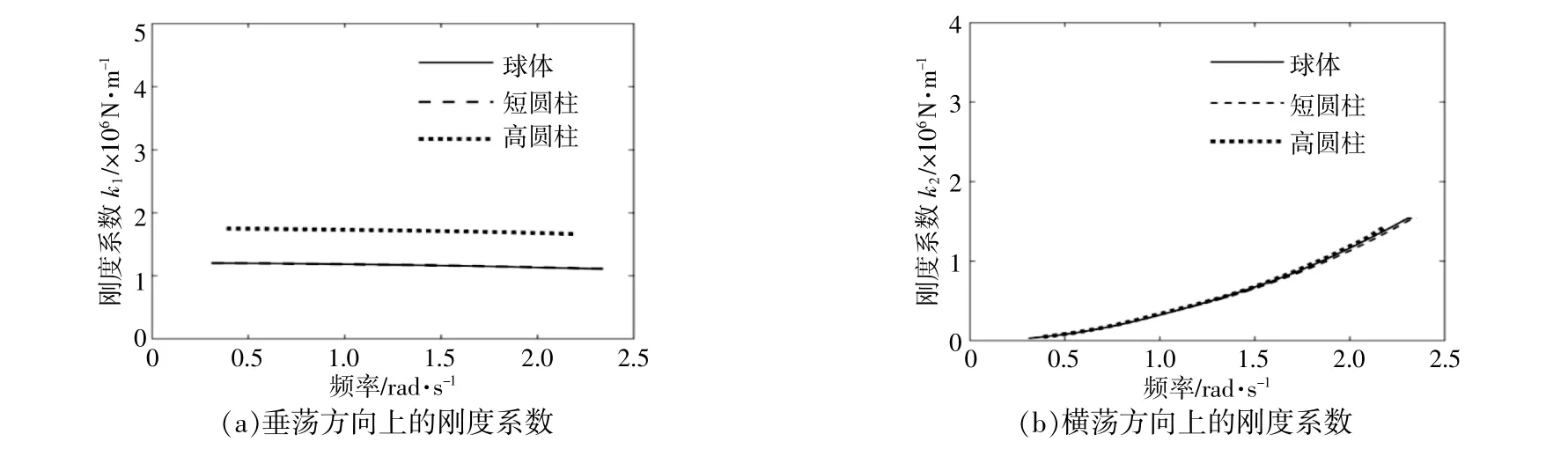
图7 不同形状波浪能装置的刚度系数Fig.7 The stiffness coefficients of wave energy converters of the investigated shapes

图8描述了3种形状WEC由式（10）～（12）优化后得到的阻尼系数。从图8（a）可见：阻尼对运动的影响非常明显，阻尼系数的波谷对应WEC运动幅值的波峰；在垂荡方向上，高圆柱WEC的阻尼系数高于另外两种形状的WEC，这限制了高圆柱WEC除峰值外的运动，导致了能量带宽变窄。从图8（b）可见：在横荡方向上，3种形状WEC的阻尼系数差距不明显；随着频率的逐渐增大，阻尼曲线呈先降再升最后再降的变化趋势，第一个波谷对应的是横荡运动的折点；波谷前较高的阻尼值主要是由横荡方向的运动约束引起的。由图8可知，垂荡方向的阻尼系数比水平方向要高1～2个数量级，这造成了WEC在垂荡方向的运动幅值小于横荡方向的运动幅值。WEC的功率与阻尼呈一次方关系，与运动幅值呈二次方关系，横荡运动吸收的能量对功率的贡献更为显著。

图8 不同形状波浪能装置的阻尼系数Fig.8 The damping coefficients of wave energy converters of the investigated shapes

固有频率是结构体的重要特性，对物体的运动有着至关重要的意义。图9描述了3种形状WEC在不同来波频率下的固有频率（图中：ωs1为外壳在横荡方向的固有频率；ωs2为内置球在横荡方向的固有频率；ωh1为外壳在垂荡方向的固有频率；ωh2为内置球在垂荡方向的固有频率）。

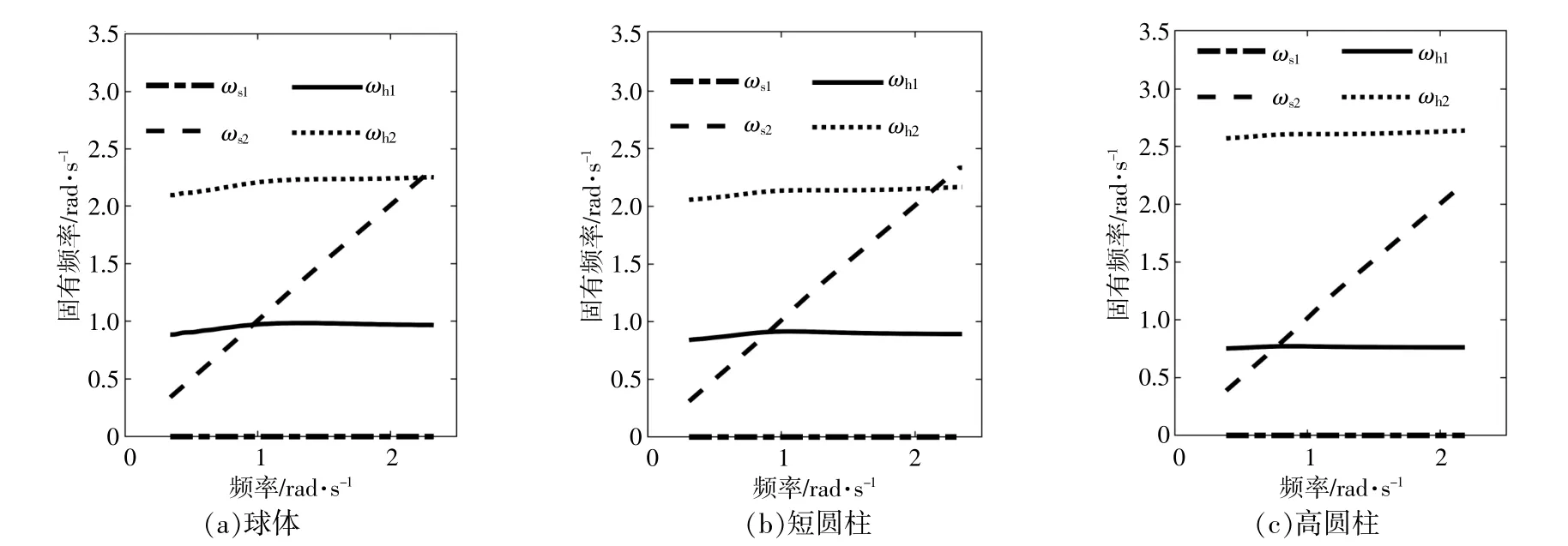
图9 不同形状波浪能装置的固有频率Fig.9 Natural frequencies of wave energy converters of the investigated shapes

从图9可以看出：3种形状WEC的ωs2曲线在低频处均与ωh1曲线相交，在高频处与ωh2曲线相交；外壳形状对固有频率的整体变化趋势影响不大，但对具体的频率值有细微影响。结合图4～6和图9可以看出，3种形状WEC在低频交点处的运动幅值和功率明显增大并出现峰值，在高频交点处有微小波峰。这两个峰的共振模式并不相同，低频峰是在入射波作用下由内置球横荡方向运动与外壳垂荡方向运动发生共振引起的；高频峰是在入射波作用下由内置球在横荡方向和垂荡方向发生共振引起的。3种形状WEC的最终优化结果：让内置球横荡方向的固有频率与波浪输入频率始终保持一致，整个系统以内置球横荡方向运动与其他运动的耦合共振为优化方向。这一结论可以为后续内置PTO式WEC的设计提供参考，在进行设计时需着重考虑内部振子以及装置在横荡方向上的运动性能。

为了深入了解WEC在发生共振时的运动状况，本文选取了共振频率下的3种形状WEC作为研究对象，通过分析其运动轨迹来探究规律。在入射波的激励下，外壳垂荡运动和内置球横荡运动会在WEC的共振频率下发生共振。图10～12分别描述了短圆柱WEC、球体WEC和高圆柱WEC在其共振频率下的运动轨迹和模态。

图10 短圆柱WEC的运动轨迹和模态Fig.10 Trajectory and mode shape of short cylinder WEC

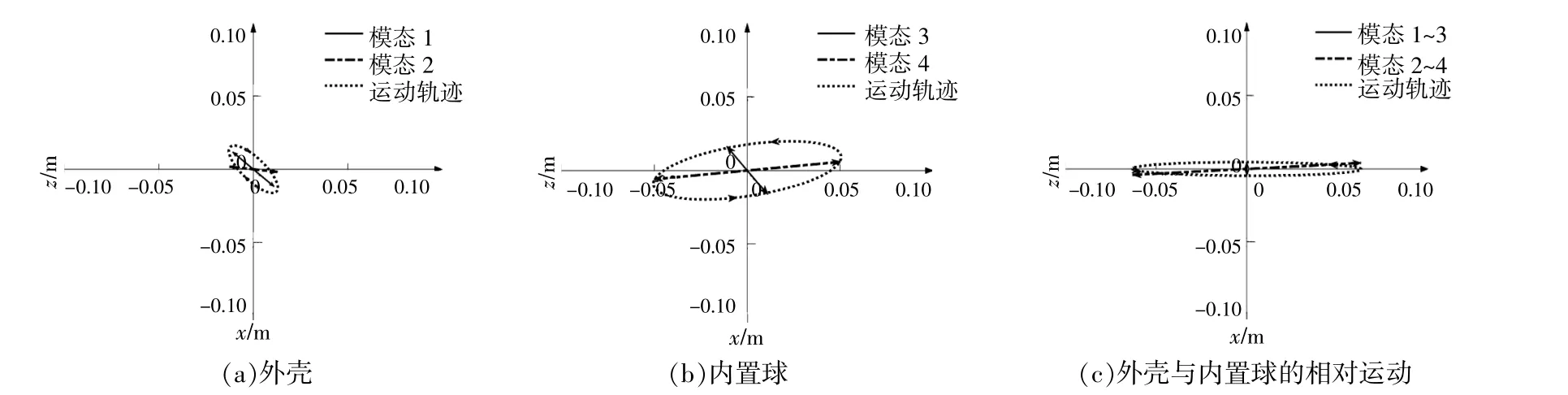
图11 球体WEC的运动轨迹和模态Fig.11 Trajectory and mode shape of sphere WEC

图12 高圆柱WEC的运动轨迹和模态Fig.12 Trajectory and mode shape of tall cylinder WEC

在图10（a）中：模态1是外壳垂荡运动主导的，模态2是外壳横荡运动主导的；外壳的横荡运动和垂荡运动的振幅较小，总体的吸能效果有限；模态1和模态2之间的相位差为222°，模态1在入射波影响下发生共振，振幅比模态2大；对于共振频率下的外壳，垂荡方向的运动对其影响更大。在图10（b）中：模态3是内置球垂荡运动主导的，模态4是内置球横荡运动主导的；模态3和模态4之间的相位差约为66.2°，模态4在入射波影响下发生共振，幅值约为模态3的2倍；在共振频率下，内置球受横荡方向运动的影响更大。在图10（c）中：模态1～3代表外壳和内置球在垂荡方向上的相对运动，而模态2～4代表外壳和内置球在横荡方向上的相对运动；模式1～3和模态2～4的相位差接近零，意味着振幅几乎沿x和z轴振荡；垂荡和横荡方向的运动几乎同时达到峰值和谷值，由于横荡方向的运动幅值远大于垂荡方向，相对运动的椭圆形轨迹的纵横比相当高，吸收能量的效果有限。由于WEC依靠外壳和内置球之间的相对运动发电，所以相对运动的轨迹决定着WEC的效率。

结合图10，11可以看出，球体WEC和短圆柱WEC的运动轨迹基本一致。结合图10～12可以看出：高圆柱WEC的外壳和内置球在垂荡方向的运动幅度大于球体WEC和短圆柱WEC；高圆柱WEC的内置球的运动轨迹接近圆形，这表明内置球在共振频率下有较好的运动表现；高圆柱WEC的外壳和内置球的相对运动轨迹整体呈现扁椭圆形，轨迹形状略优于球体WEC和短圆柱WEC，但幅值比前两者小，运动表现没有明显优势。从3种形状WEC的运动表现可总结出，内置PTO式WEC整体的吸收效果有待提高。短圆柱WEC在横荡方向上的运动振幅远高于垂荡方向，可以将该类装置应用于横荡方向能吸收更多波能的场景。在设计短圆柱WEC时，考虑到其他频率的运动表现，应该在横荡方向上设置更小的运动约束以达到更好的功率输出效果。

3 结论

本文基于模态分析法探究了一种多自由度内置PTO式波浪能装置的运动特性和输出功率之间的关系，为后续形状优化提供指导思想。本文选取了球体、短圆柱和高圆柱3种形状的外壳，在势流理论的基础上建立WEC的四自由度频域模型并进行优化，求解WEC在不同频率范围内的输出功率、相对RAO、相对速度、刚度系数、阻尼系数、固有频率以及运动轨迹。通过分析可以得出以下结论。

①短圆柱WEC和球体WEC的输出功率峰值比高圆柱WEC低，但是能量捕获带宽比高圆柱WEC宽约一倍，更适合在真实海况中工作；适当加大WEC外壳的宽高比有利于增大能量捕获带宽，吸收更多能量。

②对于短圆柱WEC，其横荡方向运动对输出功率的影响比垂荡方向运动更显著。在设计短圆柱WEC时，可着重考虑其在横荡方向的运动性能。

③内置PTO式WEC的优化结果：内置球横荡运动的固有频率与入射波频率始终一致，以内置球横荡运动与其他运动的共振为优化方向。内置PTO式WEC有两种不同的共振模式，低频时内置球横荡方向运动与外壳垂荡方向运动的共振是造成运动幅值和输出功率峰值的主要原因。3种外壳形状对系统的共振模式影响不大，但对具体的频率值有细微影响。