基于可靠性的动车组电机吊架多目标优化设计
李永华,杜江,黄漪婕,王登龙
(大连交通大学 机车车辆工程学院,辽宁 大连 116028)
随着高速轨道车辆技术的发展,结构轻量化设计成为高速动车组技术的重要研究内容之一.但结构轻量化设计与结构强度、刚度等存在一定冲突,应综合权衡各性能指标[1].动车组电机吊架的作用是将牵引电机固定在转向架构架上,其结构一旦出现问题将直接影响列车的平稳驱动和高速运行.
传统的确定性优化设计往往会忽略几何尺寸、材料参数等不确定性因素对输出响应的影响,因此可能使输出响应超出约束边界,使得优化设计不满足要求[2].可靠性优化设计能综合考虑不确定性因素的影响,使优化设计更符合工程实际.尚宝平等[3]针对现有铣削工艺参数优化过程中忽略不确定性因素的问题,采用近似模型与序列近似规划进行可靠性优化设计,有效降低加工表面粗糙度,满足最大铣削力的可靠性要求.王琼等[4]考虑汽车正面碰撞中某些不确定性参数的影响,建立一种混合不确定可靠性优化模型,实现轻量化目标并提高结构可靠性与乘员安全性.陈志英等[5]针对采用Monte Carlo模拟进行稳健优化效率低的问题,提出一种基于均值一次二阶矩并结合分位数区间的稳健优化设计方法,在保证计算精度的同时大幅度提高计算效率.目前,对电机吊架的研究主要为确定性仿真分析,尚未将参数的不确定性考虑在内,设计过程中忽略了结构可靠性的重要性,因此对其进行多目标可靠性优化具有一定的研究意义.
本文以动车组电机吊架为研究对象,通过对其进行可靠性及灵敏度分析,选择对结构应力影响较大的关键板件作为优化变量,结合多项式响应面法与均值一次二阶矩法建立多目标可靠性优化数学模型,采用多目标算法求解,该方法可以在提高结构的可靠性与稳健性的同时实现电机吊架的轻量化设计.
1 多目标可靠性优化方法
1.1 近似模型
在优化过程中直接调用有限元模型会大大增加计算时间,计算成本高.而采用适合的近似模型可以较为精准地预测出响应与输入变量之间的关系,进而代替仿真计算.针对低阶非线性问题,多项式响应面模型具有较高的拟合精度并且拟合效率要优于其他近似模型,因此,本文采用多项式响应面模型,其函数形式为[6]:
(1)
式中:b0为常数修正项;bi为线性项系数;bij为二次项系数;xi、xj为输入变量(i,j=1,…,n).所有系数根据仿真试验获取的样本点数据利用最小二乘法进行回归待定.
为评价多项式响应面函数对数据的拟合精度,使用评价指标复相关系数R2进行检验[7],其表达式为:
(2)

1.2 均值一次二阶矩方法
均值一次二阶矩法(MVFOSM)将非线性极限状态函数在均值点泰勒展开,保留线性项部分近似计算函数均值及方差,进而定义结构可靠性指标.根据应力-强度干涉理论,建立极限状态方程为Z=R-S(R为结构材料屈服强度,S为结构最大等效应力),函数Z可以通过输入变量X=[x1,x2,…,xn]表示为Z=f(X).因此,将函数在均值点μx=[μx1,μx2,…,μxn]处泰勒展开得到[8]:
(3)
根据输入变量X=[x1,x2,…,xn]的均值与方差计算Z的均值与方差为:
μZ=E(Z)=f(μx1,μx2,…,μxn)
(4)
(5)
结构可靠性指标定义为[9]:
(6)
结构可靠度与可靠性指标的关系为[10]:
Pr=φ(β)
(7)
式中,φ代表正态分布函数.
1.3 多目标可靠性优化模型
传统的多目标优化问题赋予各目标一定的权重,将多目标问题转化为单目标问题进行优化,由于该方法受人的主观影响,优化效果不够理想.目前,运用Pareto占优思想并结合多目标智能算法能够较好地处理多目标优化问题[11].通过在优化过程中引入可靠性约束实现多目标可靠性优化,其数学模型为:
(8)
式中,f(x)为目标函数,g(x)为约束函数,P(g(x)≤0)表示约束函数满足设计要求的概率[12],rj为可靠度期望值,xU、xL是优化变量的上下限.
综上所述,本文建立的多目标可靠性优化流程如图1所示.

图1 电机吊架多目标可靠性优化流程
2 电机吊架结构仿真分析
2.1 电机吊架有限元模型的建立
电机吊架大部分由薄板焊接而成,所使用材料为高强度耐候钢S355J2G.根据电机吊架的几何模型,使用HyperWorks中HyperMesh模块建立电机吊架的有限元仿真模型,利用T1~T10对不同位置的薄板进行编号,得到电机吊架有限元模型如图2所示.

图2 电机吊架有限元模型
该有限元模型在几何模型的基础上,清除了一些不必要的小圆孔与圆角,其余部分与几何模型保持高度一致.考虑到计算机求解效率,各板件结构使用网格大小为10 mm的四边形壳单元(Shell181)进行划分;部分结构使用少量的三角形壳单元划分;电机座衬套使用网格大小为10 mm的四面体单元(Solid185)划分.电机吊架有限 元 模型共划分50 739个单元, 节点数为30 170.根据UIC 615-4-2003《移动动力装置-转向架和走行装置-转向架的结构强度试验》添加载荷工况进行强度分析.
2.2 静强度分析
将电机吊架的有限元模型导入至ANSYS软件进行静强度分析,再将分析后的结果文件导入HyperView模块中查看等效应力计算值,电机吊架等效应力云图如图3所示.

图3 电机吊架等效应力云图
根据等效应力云图可以看出,电机吊架最大等效应力值为336.9 MPa,出现在肋板处(板件编号为T9).由于电机吊架所使用材料的屈服强度为345 MPa,最大等效应力值较为接近材料屈服强度,由于不确定性因素的影响,应力值可能超出材料屈服强度,使结构发生强度失效,因此进一步分析其可靠性.
2.3 可靠性及灵敏度分析
基于ANSYS中PDS模块采用Monte Carlo法进行电机吊架的可靠性及灵敏度分析.各随机输入变量的分布形式及参数见表1[13].

表1 随机输入变量的分布形式及参数
在输入变量的分布区间内采用拉丁超立方方法进行1 000次抽样,定义输出变量为Z,根据Z值判断结构强度是否符合材料屈服极限的要求.

(9)
通过Monte Carlo法定义电机吊架的可靠度为:
(10)
式中,n为Z值大于零的抽样次数,N为抽样总次数.
进行1 000次抽样后,最大等效应力的抽样结果如图4所示,由图可以看出其样本均值趋于平稳(置信水平为95%),说明抽样次数足够.最大等效应力的概率密度分布直方图如图5所示,通过样本抽样估计,得到最大等效应力总体近似服从均值为336.9 MPa,标准差为16.55的正态分布.通过Monte Carlo法计算电机吊架的静强度可靠度为71.7%.通过可靠性分析可知此结构有较大概率会发生强度失效,可靠度具有很大的优化空间.因此,有必要对电机吊架进行可靠性优化设计.

图4 电机吊架最大等效应力均值趋势图

图5 电机吊架最大等效应力概率密度直方图
灵敏度分析表明各输入变量对最大等效应力的影响程度,分析结果如图6所示.其中编号为T8的板件对应力影响不显著,在图中不予显示.
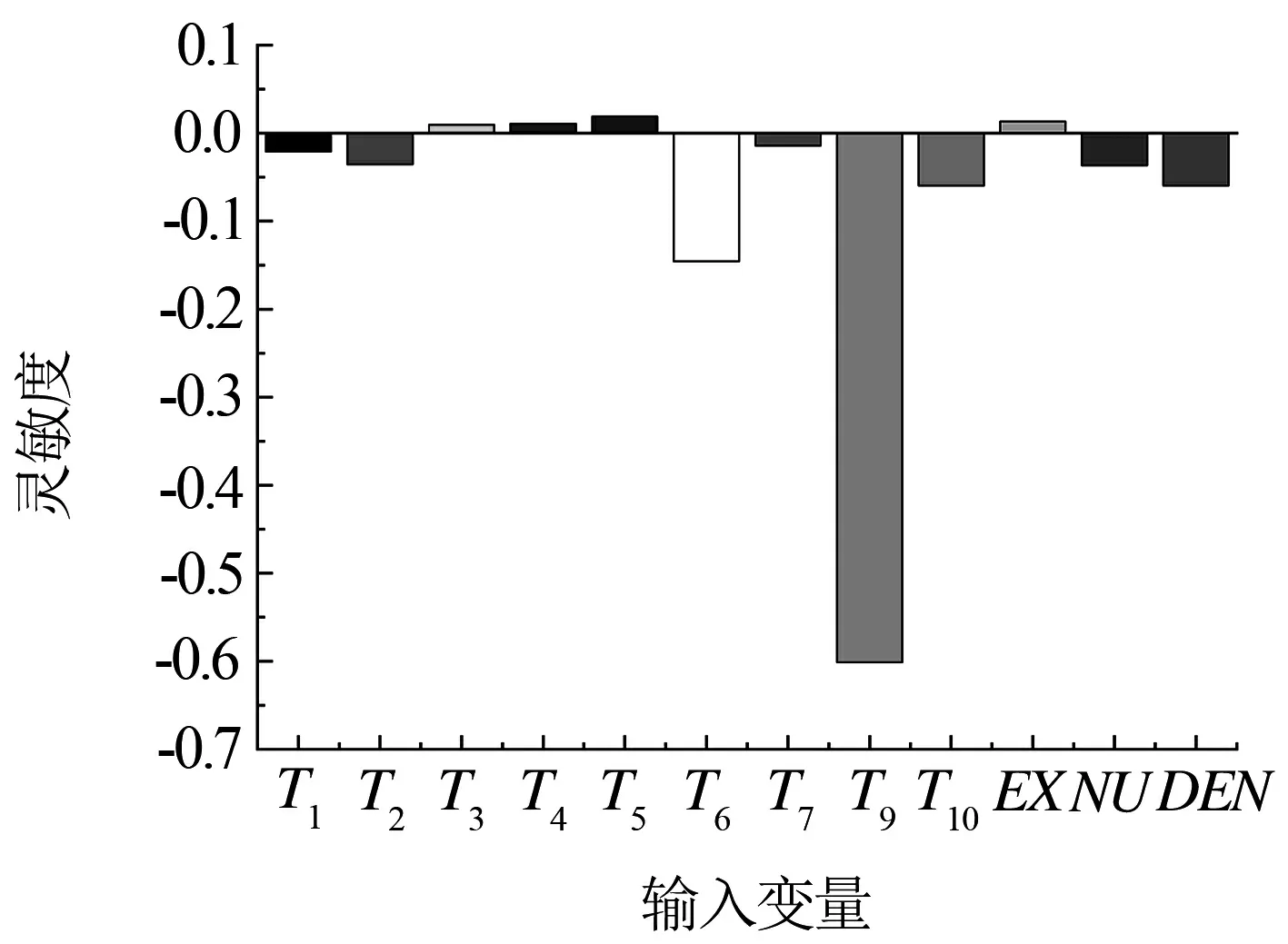
图6 电机吊架最大等效应力灵敏度
通过图6可以看出,最大等效应力与变量T3、T4、T5、EX呈正相关,与变量T1、T2、T6、T7、T9、T10、NU、DEN呈负相关.柱状图的绝对高度越高,表示输入变量对应力的影响程度越大.为提高优化效率,可以只关注灵敏度大的输入变量,因此,选取用T6、T9、T10表示的三个厚度参数值作为优化变量.
3 电机吊架多目标可靠性优化
3.1 仿真试验设计
基于Isight平台搭建仿真试验设计流程,在cdb文件中添加提取最大等效应力、质量的命令,建立批处理文件实现ANSYS的自动计算,将各设计变量、最大等效应力、质量的数值均映射到Isight中,采用最优拉丁超立方抽样方法进行均匀采样[14],得到30组抽样数据见表2.

表2 试验设计样本点数据
3.2 拟合响应面函数
根据已获得的30组抽样数据,利用最小二乘法计算各待定系数,得到应力fS、质量fM关于输入变量的多项式响应面函数表达式如下:
(11)
(12)
经过检验,结构最大等效应力与质量的多项式响应面函数的复相关系数R2分别为0.999、1.0.说明响应面函数的拟合效果良好、具有足够的精度,可以代替有限元计算.
将fS在均值点进行泰勒展开,舍去高阶项,保留线性项部分,根据输入变量的方差近似计算应力的方差为:
(13)
建立极限状态函数为Z=R-fS,将应力函数代入方程得到下式:
(14)
采用MVFOSM法对极限状态函数进行均值估计与方差估计,得到均值函数与方差函数为:
(15)
(16)
根据结构可靠性指标的定义,通过均值函数与方差函数的比值获得可靠性指标函数.将各变量均值代入得到结构可靠度为69.8%,可见MVFOSM法相比于Monte Carlo法误差较小.针对本文模型,MVFOSM法满足计算精度要求,并且计算时间远小于Monte Carlo法,计算效率得到大幅度提升.
3.3 建立优化数学模型
经过上述计算,建立电机吊架多目标可靠性优化数学模型为:
(17)
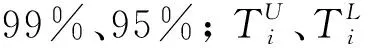
3.4 优化结果
采用第二代非支配排序遗传算法(NSGA-Ⅱ)对本文建立的数学模型进行多目标优化.设置算法的种群规模为60,遗传代数为50,交叉率为0.9,变异率为0.1.通过迭代计算得到的Pareto最优前沿如图7所示.

图7 Pareto最优前沿
通过图7可以看出,Pareto最优前沿分布均匀,图中每个点分别代表一组最优解,各个解之间互相不支配.由于目标之间的冲突,结构质量随着应力标准差的减小而增加,设计人员可以根据侧重点的不同选择相应的解.本文考虑质量解的变化范围相对较小,增加较小的质量可以使应力标准差下降的更多,因此,在最优解集中选择偏向于标准差更小的解.本文选定一组优化方案,根据工程制造实际,将各优化板件的厚度值进行圆整,将圆整后的各参数值写入到仿真分析文件中,再一次对电机吊架进行静强度及可靠性分析,得到电机吊架优化设计前后各参数值对比,见表4.

表4 优化设计前后各参数值对比
由表4可知,通过对电机吊架进行多目标可靠性优化,提高了结构可靠度、减轻了电机吊架的质量、降低了应力标准差.结果表明各性能指标均得到一定程度的优化,说明此多目标可靠性优化方法有效、可行.
4 结论
(1)通过对高速动车组电机吊架有限元模型进行强度校核与可靠性分析,筛选出对应力影响较大的关键板件并将其厚度参数值作为优化变量;
(2)基于应力-强度干涉理论,提出一种结合多项式响应面法与MVFOSM法的多目标可靠性优化设计方法,并采用多目标算法进行求解;
(3)优化设计后,电机吊架的最大等效应力降低5%、结构可靠性提高至98.9%、应力标准差降低27%、结构质量减轻6.4%.实现了电机吊架减重的目的并提高了结构稳健性,同时结构可靠性满足要求.为电机吊架及其他结构的多目标可靠性优化提供参考.

