考虑极限应力相对量度的Manson-Coffin改进模型
蒋广龙,高月华,刘其鹏,2
(1.大连交通大学 土木工程学院,辽宁 大连 116028;2.南昌航空大学 航空制造工程学院,江西 南昌 330063;3.大连交通大学 机车车辆工程学院,辽宁 大连 116028)
低周疲劳破坏是工程结构中常见的一种失效形式,大多数研究者把失效循环数低于104~105次的疲劳定义为低周疲劳[1].现有的低周疲劳寿命预测模型主要有Manson-Coffin模型、应力场强法和三参数幂函数能量法等,这些模型就是将疲劳寿命与循环应力、应变幅和循环滞回能等参量联系在一起得到的[2-3].其中,Manson-Coffin模型在工程中得到了广泛的应用,然而该模型更适用于对称循环载荷加载的情况,实际工程中的疲劳载荷几乎都是非对称循环载荷.在载荷从最小值变化到最大值的过程中会产生平均应力,研究[4-5]表明,平均应力会影响到裂纹的扩展速度,进而会对疲劳寿命产生影响.因此,在非对称循环载荷下进行疲劳寿命预测时,需要对Manson-Coffin模型进行平均应力修正.早在1968年,Morrow就将平均应力修正准则引入到Manson-Coffin模型中来考虑平均应力的影响[6].Smith等假设通过SWT参数来确定一个循环周期中的疲劳损伤量[7].Dowling结合Walker平均应力修正准则和Manson-Coffin模型得到了包含应力比修正的应变-寿命方程[8].Kwofie基于平均应力直接影响疲劳强度系数σf′的前提,提出了一种指数应力函数来反映平均应力对疲劳寿命的影响[9].吕志强将平均应力灵敏系数γ引入到SWT参数模型,得到了预测精度更高的修正模型[10],但这些Manson-Coffin改进模型针对不同材料的预测结果具有较大的分散性,且预测精度仍有待进一步提高.
本文在考虑平均应力对疲劳寿命的非线性影响的基础上,进一步考虑屈服极限和强度极限的相对量度对平均应力以及疲劳强度系数σf′的影响关系,对Manson-Coffin模型进行改进,并采用三种常用材料的非对称加载试验数据,通过与既有改进模型对比分析,对本文改进模型进行有效性和可行性验证.
1 Manson-Coffin模型及既有改进模型
应变-寿命曲线是用于表示结构应变和疲劳寿命之间的关系,其中最通用的应变寿命预测模型是由Basquin在1910年提出的,用以表示弹性应变εea和疲劳寿命N之间的关系,其表达式为[11]:
(1)
式中,σf′为疲劳强度系数,b为疲劳强度指数,E为弹性模量,Nf为疲劳寿命.由于Basquin公式没有考虑平均应力对疲劳寿命的影响,而且只能对以弹性应变为主的结构进行疲劳寿命预测.对此,1954年,Manson和Coffin在独立研究热疲劳问题的过程中分别提出了一种以塑性应变幅εpa为参量的寿命模型[12]:
εpa=εf′(2Nf)c
(2)
式中,εf′为疲劳延性系数,c为疲劳延性指数.在恒幅应变疲劳试验中,总应变幅εa可以写成弹性应变幅εea和塑性应变幅εpa之和,即Manson-Coffin公式:
(3)
对于Manson-Coffin模型,它是在对称循环载荷下提出的,没有考虑平均应力对疲劳寿命的影响.但是之后的试验证明,平均应力对结构疲劳寿命的影响不可忽略,一般情况下,拉伸平均应力对疲劳寿命具有削弱作用,压缩平均应力对疲劳寿命具有促进作用,本文主要考虑拉伸平均应力.针对Manson-Coffin模型未能考虑平均应力影响的缺点,Morrow提出了相应的平均应力修正准则,并将其引入到Manson-Coffin公式中提出了仅对结构弹性应变部分进行平均应力修正的模型[6]:
(4)
(5)
式中,σar=σf′(2Nf)b为等效对称应力幅值,σa为循环应力幅值,σm为平均应力.
同样地,Smith、Watson和Topper也提出了一种平均应力修正准则(SWT平均应力修正准则):
(6)
式中,σmax=σm+σa是最大应力值.同时他们认为在给定疲劳寿命下,最大应力σmax和循环应变幅εa两者的乘积会保持不变,因此假设在一个循环周期中的疲劳损伤量是通过SWT参数σmaxεa确定的,并结合式(6)提出了SWT参数模型[7]:
(7)
对比式 (4)~(7) 可以看出,两种改进模型都是在Manson-Coffin模型的基础上对疲劳强度系数σf′进行修正,Morrow改进模型假设疲劳强度系数σf′与平均应力σm之间是一次函数关系,而SWT参数模型则是假设两者之间是幂函数关系.文献[9]则认为疲劳强度系数损伤的严重程度取决于平均应力σm和强度极限σb之间的相对量度,并采用指数应力函数的形式来反映疲劳强度系数σf′与平均应力σm之间的非线性关系,即:
(8)
Nk=Nfexp(-σm/σb)1/b
(9)
2 Manson-Coffin模型的改进
根据Basquin公式可知,疲劳强度指数b通常为负值,当应力幅值一定时,疲劳寿命Nf和疲劳强度系数σf′为正比关系,由于平均应力使疲劳裂纹尖端保持张开,能够加速疲劳损伤的累积过程,使得疲劳寿命减少,从而引起σf′的降低,即可以假定σf′是σm的某一函数,即σf′=f(σm).大量的理论和试验数据证明,材料的疲劳寿命在加载的过程中以非线性函数的形式变化,因此假定疲劳强度系数和平均应力这两者之间是非线性函数关系是可取的,符合疲劳裂纹扩展的规律.
需要注意的是,一方面,只有当施加的最大应力小于材料的强度极限时,才会发生疲劳破坏而不是单调破坏,而屈服极限是表征工程材料塑性行为及其相关疲劳性能的关键指标,其对于低周疲劳寿命的影响也是不可忽略的.Soderberg曾提出一种极限应力线来补偿拉伸平均应力的影响,将屈服极限引入到平均应力修正准则中,以此来考虑屈服极限的影响[13],但后续试验表明只考虑屈服极限而得出的结果会比较保守[14],因此应该综合考虑强度极限和屈服极限两个因素.另一方面,因为材料的力学性能差异,不同材料的平均应力效应明显不同,文献[10]认为材料对平均应力影响的灵敏度和屈服极限、强度极限存在一定的内在联系,由此可得平均应力对每种材料疲劳寿命的影响程度与屈服极限σs和强度极限σb有关.综上,可以认为疲劳强度系数σf′的平均应力损伤程度与屈服极限和强度极限的相对量度σs/σb有关.
考虑到文献[9]通过平均应力与强度极限的相对量度σm/σb的指数应力函数形式来体现平均应力对疲劳强度系数的非线性影响具有较好的预测性能,本文改进模型中亦将相对量度σm/σb作为基本变量,并采用指数应力函数形式对疲劳强度系数σf′进行修正.根据上述分析,对疲劳强度系数σf′进行平均应力修正时,除考虑相对量度σm/σb的影响外,还需进一步考虑屈服极限和强度极限的相对量度σs/σb对平均应力以及疲劳强度系数的影响.此外,在低周疲劳区域,塑性变形会减弱或消除平均应力对疲劳强度的影响,因此主要考虑弹性部分的平均应力修正.综上,给出改进的预测模型为:
(10)
3 算例及对比分析
为验证本文改进的Manson-Coffin模型的疲劳寿命预测能力,采用SAE 1045 HRC 55钢、7075-T651铝和16MnR钢[4,15-16]三种材料的低周疲劳寿命试验数据进行疲劳寿命预测,同时为验证改进模型的有效性和准确性,将其疲劳寿命预测结果与其他改进模型的预测结果进行对比分析.
SAE 1045 HRC 55、7075-T651和16MnR三种材料的疲劳性能参数的试验值见表1,表2~表4分别给出了三种材料的疲劳寿命试验值和不同模型的预测值,表中应力σ单位均为MPa,疲劳寿命N的单位均为cycle.由表2~表4的结果可以看出,本文改进模型的预测结果比较接近试验值,具有较高的预测精度.为了量化不同模型的疲劳寿命预测误差,这里采用文献[17]中的方法,定义预测对数寿命与试验对数寿命之差δ为预测误差,即:

表1 SAE 1045 HRC 55、7075-T651和16MnR疲劳性能参数
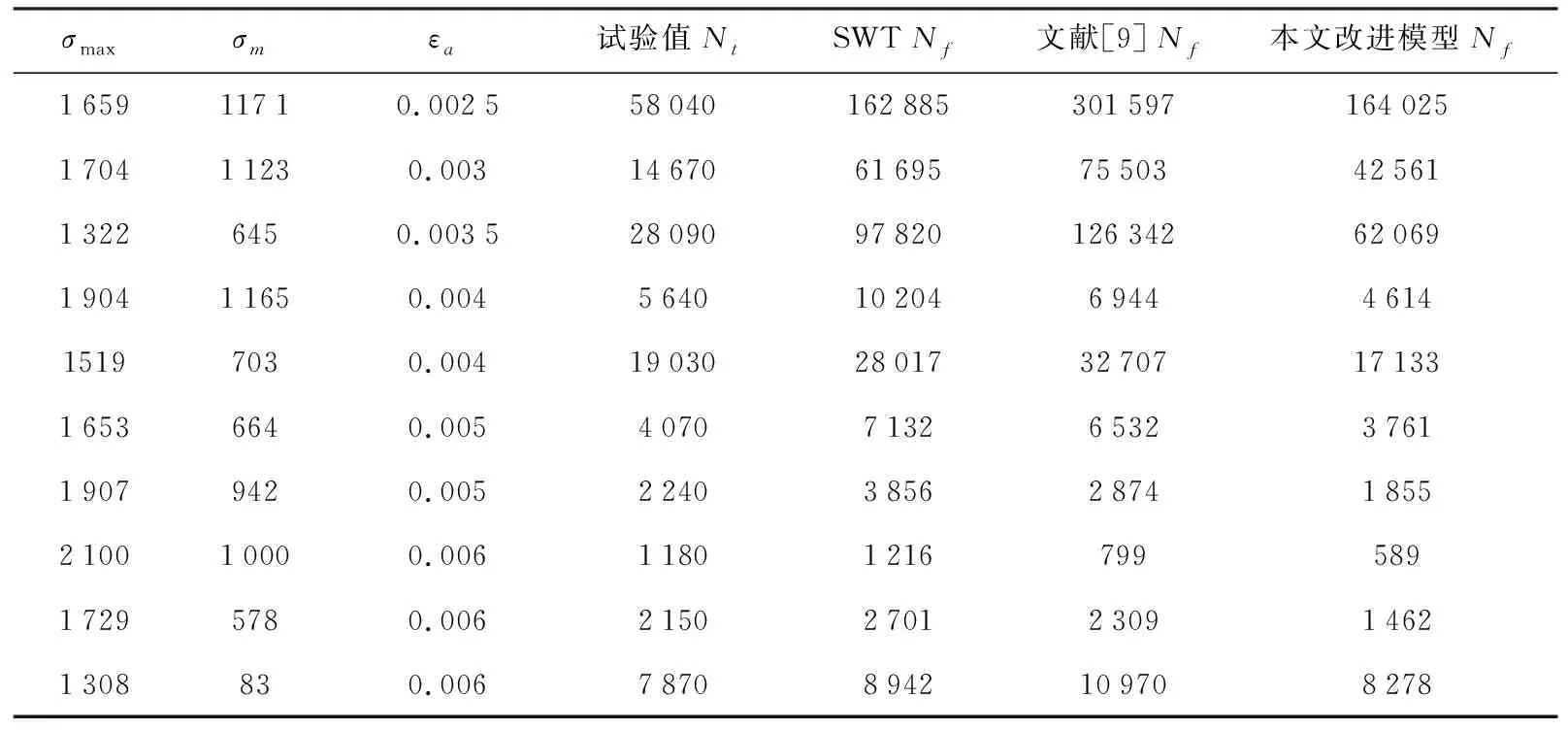
表2 SAE 1045 HRC 55钢疲劳寿命试验值和不同模型预测值
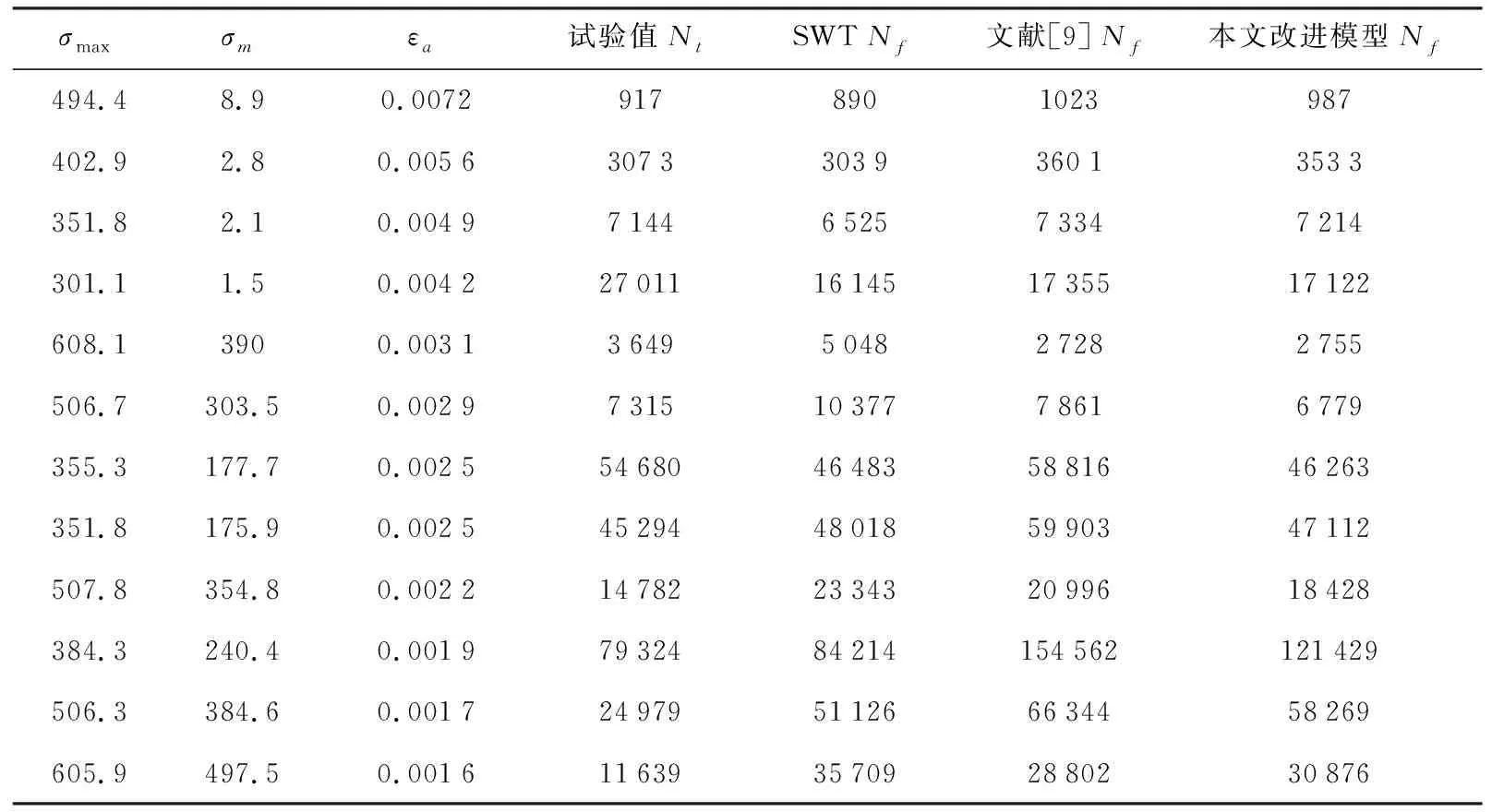
表3 7075-T651铝疲劳寿命试验值和不同模型预测值
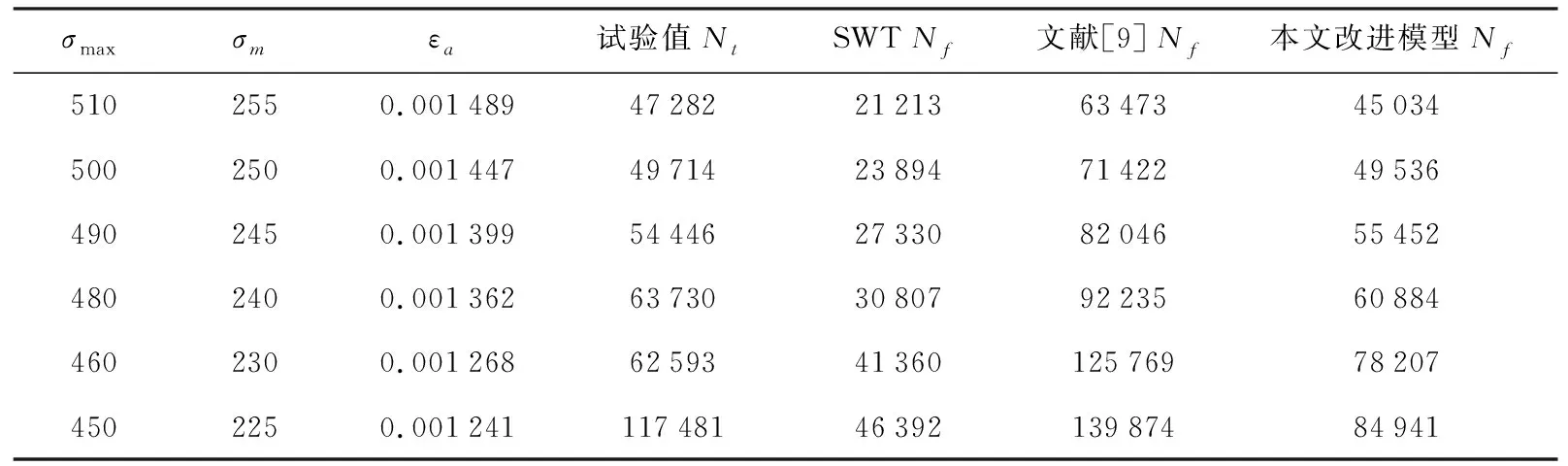
表4 16MnR钢疲劳寿命试验值和不同模型预测值
δ=lg(Nf)-lg(Nt)
(11)
均方差是总结模型预测误差集中趋势和扩散的良好统计量,计算均方差作为寿命预测模型的度量, 不同模型的疲劳寿命预测的均方差值见表5.
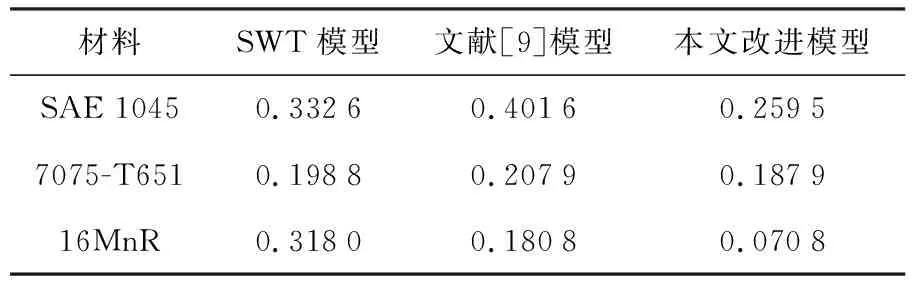
表5 不同模型疲劳寿命预测的均方差值
由表5的计算结果可知,本文改进模型对各个材料的寿命预测均方差值均最小,偏离试验值的程度最低,显示了良好的预测稳定性、准确性和适用性.
图1(a)~1(c)分别针对三种材料,将本文改进模型的疲劳寿命预测结果与SWT参数模型和文献[9]中模型的预测结果进行了对比.
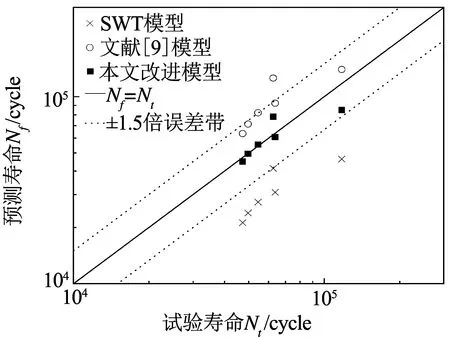
(c)16MnR钢图1 不同模型疲劳寿命预测值对比
从图1可以看出,对于SAE 1045 HRC 55钢,本文改进模型预测结果最优,明显优于SWT参数模型和文献[9]模型的预测结果,三种模型分别有60%、30%和40%的数据位于±1.5倍误差带内;对于7075-T651铝,三种模型的预测结果比较接近,大部分数据均在±1.5倍误差带内,预测精度均较高,本文改进模型略优于其他两种既有模型,同时显示了SWT模型对于铝制材料的预测效果也较好;对于16MnR钢,本文改进模型的预测结果十分接近试验值,预测数据均在±1.5倍误差带内, 预测精度显著高于SWT参数模型和文献[9]模型,其中SWT参数模型的预测结果最差,预测数据几乎都在1.5倍误差带以外.综上,本文改进模型对非对称载荷下结构的低周疲劳寿命预测是比较有效和准确的,相比于传统Manson-Coffin模型、SWT模型以及文献[9]模型,本文改进模型的预测精度均有较为明显的提高.
4 结论
(1)为了解决平均应力对疲劳寿命影响的问题,在采用相对量度σm/σb的指数应力函数形式基础上,引入屈服极限和强度极限的相对量度σs/σb来修正疲劳强度系数σf′,以此对Manson-Coffin模型进行改进.所提出的改进模型反映出了疲劳强度系数和平均应力之间的非线性关系以及极限应力之间的相对量度对两者之间关系的影响;
(2)采用三种常用材料的疲劳试验数据,对改进模型的合理性和有效性进行验证,结果显示本文改进模型的预测结果与试验数据吻合良好,疲劳寿命的预测精度相较于传统Manson-Coffin模型,其既有模型得到了明显的提高,且形式较为简单,便于应用于工程结构的疲劳寿命预测.

