基于子模型法的牵引梁结构优化设计
曾子铭,孙丽萍,王玉艳,孙业琛,卢佳妮
(大连交通大学 机车车辆工程学院,辽宁 大连 116028)
随着我国铁路行业的快速发展,特别是客运专线和高速铁路的相继开通,工程轨道车的投入量逐渐增长.在机车车辆设计制造过程中,车体结构的静强度计算不仅可以对车体结构的强度和刚度进行校核、指导结构改进,而且在提高机车车辆运营可靠性方面也发挥着重要作用[1-2].车辆在运行过程中,牵引梁主要用于传递轨道车辆纵向拉伸或压缩载荷,能够将来自车钩装置的纵向力传递到底架,其结构可靠性直接关系到车辆的运营安全[3].因此,在设计阶段对牵引梁进行高效的强度校核是一项必不可少的工作.
本文针对牵引梁后盖板在强度校核中安全系数不满足设计要求的问题,采用子模型法和拓扑优化对其结构开展优化研究.这样不仅减小计算规模,提高了设计效率,同时可为 未来相关板类的设计提供有益参考.
1 牵引梁结构简介
牵引梁是车体底架车钩安装和车辆承载的重要结构,其前端与缓冲梁连接,后端与枕梁连接,左右两侧分别通过小横梁与底架边梁焊接在一起.其主要构件由上盖板、腹板、隔板、加强筋板、后盖板和托板等组成,材质均为耐候钢(Q345),结构如图1所示.
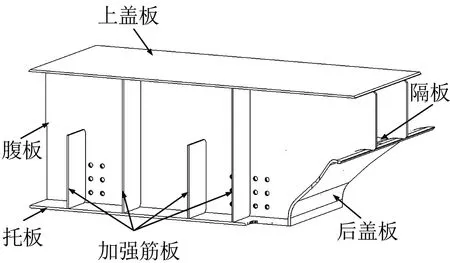
图1 牵引梁结构
根据设计要求,结构强度需小于材料的屈服极限且安全系数需大于等于1.1.牵引梁结构确定后,对其进行静强度分析时发现:压缩工况下,强度的最危险部位发生在牵引梁后盖板,数值为335.5 MPa,虽然应力值小于材料的屈服极限,但是其安全系数为1.03,不满足设计要求.因此,为了提高设计效率,结合子模型法对其结构重新进行优化设计.
2 子模型法简介
子模型法基于圣维南原理,是在计算分析整体模型基础上,对局部部件采取相关研究的一种方法,同时子模型法也被称为切割边界或特定边界位移法.切割边界指的是将所研究的部件的边界从整体模型中分割出来,获得的位移信息作为子模型基本的边界条件[4],进而将子模型从整体模型中提出来开展下一步的研究.子模型法可以从有限元理论中得到证明,而有限元求解的本质是线性方程组求解,具体可以表达为:
[K][D]=[F]
(1)
式中,[K]为整体刚度矩阵,[D]为待求的位移向量,[F]为外载荷.
假设位移向量[D]中,已知部分为[D1],其余部分为[D2],则上式可以改写为
(2)
其中,式(2)展开可以得到:
K22·D2=F2-K21·D1
(3)
由此可知,位移向量[D1]已经转变为载荷项,进而可求得向量[D2],其中位移向量 [D1]即为切割边界的位移条件,这就从有限元理论角度验证了子模型法的正确性[5-6].
子模型法不仅保证了局部部件研究的准确性,也使得结构在优化研究过程中的计算量大幅度减小,进而缩短了研究人员的设计时间,提高整体的分析效率,达到了以较小的计算量实现局部结构优化的目的.
3 牵引梁子模型
根据子模型法的基本理论,将整车模型中的牵引梁提取出来,建立牵引梁子模型.具体步骤如下:
首先对整车的有限元模型开展静强度计算,得到各个工况下的应力和位移结果.基于整车有限元模型的计算结果,将牵引梁从整车有限元模型中截取出来,同时建立牵引梁子模型的相关单元集合和边界的节点集合,获得边界位移信息后删除与牵引梁子模型不相关的网格.其次将牵引梁视为单独模型开展细化研究.将获得的边界条件和位移信息重新施加到模型中,设置载荷约束从而得到牵引梁子模型.
获得牵引梁子模型后,为了确保子模型的准确性,对其进行静强度计算加以验证,通过对比牵引梁子模型和整车模型的强度和刚度可以得出:在压缩工况下的最大VonMises应力值和发生的位置以及刚度基本保持一致,因此通过验证可以认为牵引梁子模型符合要求,具备优化研究的条件.
牵引梁结构整体采用壳单元离散,尺寸大小为20 mm,最终生成了12 446个节点和12 305个单元,其有限元模型如图2所示.

图2 牵引梁有限元模型
4 牵引梁后盖板拓扑优化
4.1 拓扑优化
拓扑优化指的是寻找优化设计区域内结构材料的最优分布,在给定边界条件、载荷以及满足各项设计约束的基础上,最终达到设计目标最优的目的[7].该方法可以在设计初期或工程探索阶段为设计人员提供结构和材料的最优分布方案,设计人员依据优化结果对设计方案作出相应的调整.经过多年的发展,常见的拓扑优化方法有:均匀化方法、变厚度法、变密度法、渐进结构优化法等[8-9].
本文以变密度法为理论基础,将区间[0,1]内的密度值作为设计变量.其中0、1表示材料的去除和保留[10].通过此方法就可以实现结构的拓扑优化问题和材料的最优分布问题之间的转换,同时将拓扑变量依附于单元材料上,进而基于连续变量的优化算法进行计算,在得到了最佳的传递力的路径同时,也使得最终的设计方案更加合理、经济[11].
4.2 牵引梁后盖板结构拓扑优化
牵引梁原设计结构中,后盖板的板厚为17 mm,质量为59.93 kg.由于只有牵引梁后盖板在压缩工况下的安全系数,不满足设计要求,因此只需对牵引梁后盖板进行优化即可,所以在参考原设计结构的外形尺寸基础上,将牵引梁后盖板以及腹板和隔板连接处采用实体网格填充,填充后的实体网格数量为30 348,得到了优化设计区域实体填充模型,其如图3所示.为了计算结果更加准确,部分网格重新划分,局部区域采用三角形网格进行过渡.最终以生成的实体网格为设计区域进行拓扑优化,数学模型可以描述为:

图3 优化设计区域实体填充模型
(1)目标函数:质量分数最小化;
(2)设计变量:牵引梁后盖板实体单元的密度;
(3)约束条件:给定设计区域的VonMises应力小于310 MPa.
通过OptiStruct计算显示,牵引梁后盖板模型结构在经过99次迭代后收敛,其目标函数的迭代曲线如图4所示.

图4 目标函数迭代曲线图
优化过程结束后,其结果在HyperView中打开,通过改变不同的密度阈值以获得优化后材料分布和载荷传递路径的最佳效果.通过改变不同的阈值,可以得到不同密度阈值下的等值面图.当密度阈值为0.5时,其等值面图如图5所示,从中可以清晰地看到材料分布情况,同时也得到了牵引梁后盖板的整体的外形形状以及与腹板连接的筋板.通过测量网格的尺寸,得到后盖板的厚度为16.75 mm,圆整后板厚取17 mm.后盖板的板厚与原设计结构的厚度保持一致.

图5 密度阈值为0.5时密度等值面图
根据优化结果对牵引梁后盖板进行几何重构,同时综合考虑后盖板与其他各结构焊接关系,对牵引梁后盖板结构重新设计,得到的结构见图6所示.设计后的牵引梁后盖板与原设计结构相比,其与牵引梁托板连接处的弧度有所增加,而且在水平方向的倾斜角度更大.

图6 几何重构后的牵引梁后盖板
牵引梁后盖板结构改进之后,其强度是否满足设计要求还不清楚,因此将优化后的牵引梁后盖板放到整车模型中进行应力计算和分析.从计算结果可以看出:在压缩工况中,改进后的牵引梁后盖板的最大VonMises应力为303.2 MPa,小于材料屈服极限,达到了设计要求中规定的安全系数大于等于1.1的要求.同时最大应力发生的位置与原设计结构基本一致,其应力分布见图7所示.由此可以证明优化后的结构满足设计要求.

图7 改进后牵引梁后盖板应力云图
结合优化后牵引梁后盖板应力云图可以看出:优化后的牵引梁后盖板中间部位应力较小,材料存在冗余,可以适当去除部分质量,这在加工工艺上是很容易实现的.于是在保证后盖板外形尺寸的前提下在其中间增加减重孔,这样既减少了设计材料,又降低了结构质量,同时间接地节约了制造成本,最终得到牵引梁后盖板结构如图8所示.增加减重孔后的牵引梁后盖板在整车中的静强度计算结果为:与未增加减重孔的牵引梁后盖板相比,在压缩工况中最大VonMises应力发生的位置一致,但是应力值从303.2 MPa增加到305.9 MPa,尽管应力值增加了2.7 MPa,但是依然满足材料的屈服极限且安全系数达到1.13,显然结果满足设计要求,其应力云图如图9所示.此外,增加减重孔的牵引梁后盖板的质量为53.26 kg,与原设计结构相比,质量减少了6.67 kg,减重11.13%.而且在压缩工况下的最大位移由原来的5.23 mm变为5.29 mm,刚度变化不大.
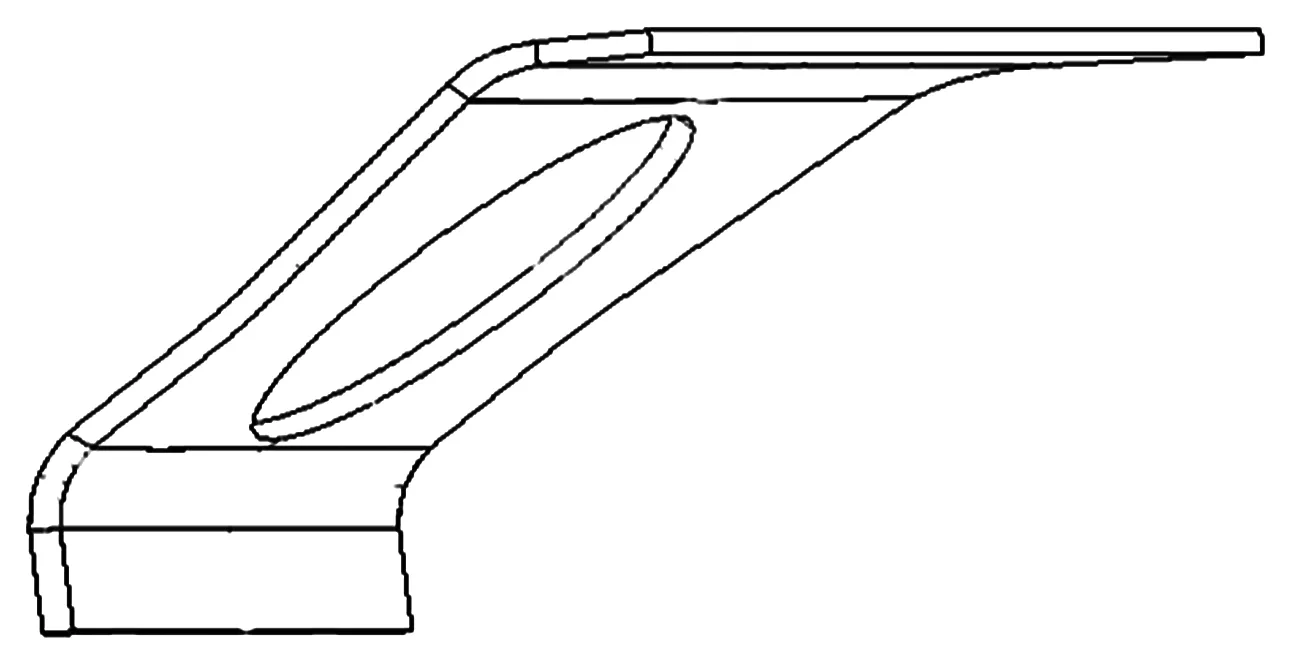
图8 增加减重孔后的牵引梁后盖板
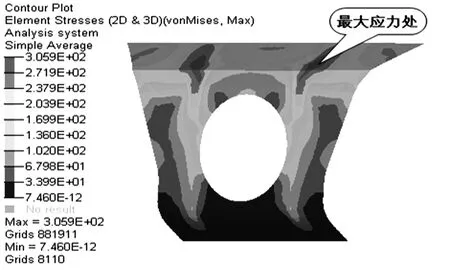
图9 增加减重孔后的牵引梁后盖板应力云图
牵引梁后盖板通过拓扑优化、几何重构以及增加减重孔后,确定了最终的设计方案.此方案不仅在压缩工况下满足设计要求,同时在其他工况下,改进后的牵引梁后盖板结构也符合设计要求.因此可以认为该方案达到了设计的预期目的.
5 结论
本文以某工程轨道车牵引梁后盖板为研究对象,利用子模型法对其进行拓扑优化.在设计过程中,子模型法的应用大幅度缩短了计算时间,而且计算精度也得到了保证.实现了以较小的计算量达到牵引梁后盖板结构优化的准确计算.同时依据拓扑优化的分析结果对牵引梁后盖板的结构进行重新设计,得到了最优方案,该方案经过整车静强度计算,安全系数达到1.13,满足设计要求.同时其质量比原设计结构减少了6.67 kg,减重11.13%,轻量化效果明显.

