全局参数估计的颜色空间转换偏振去雾算法
李荣华,唐智超,李宏亮,朴俊峰
(大连交通大学 机械工程学院,辽宁 大连 116028)
雾霾天气环境下,空气中的雾霾颗粒对大气光的吸收和散射等作用导致能见度降低,严重降低了探测器获取的图像质量,如交通监控、码头检测系统以及遥感探测系统等.目前对于如何消除雾霾影响的方法主要分为两类:一类是图像增强复原技术,主要是通过提高图像的对比度来增强图像,比如直方图均衡化、Retinex复原和小波变换等,这类算法虽然计算简单但只是增强了图像整体的效果,对于图像细节复原并不是很理想;另一类是通过大气散射模型消除雾霾,这类算法[1-2]在增强图像对比度的同时对于图像细节处的复原也能达到理想效果,因此,此类算法具有重大的研究价值和应用前景.
Fattal[3]重新定义了大气散射模型,并且在保留传输函数的基础上,增添了表面阴影这个新的变量,通过假设透射率和物体表面投影在局部区域内不相关来估计参数从而还原雾霾图像,但是在浓雾天气下此算法并不能很好的复原图像;Schchner[4]通过手动调节偏振片获取同一场景下的垂直和平行的最大、最小光强图像,通过手动选取天空区域来估算无穷远处大气光值和大气光偏振度来代替整幅图像的无穷远处大气光值和大气光偏振度,再根据偏振去雾模型得到去雾图像,此算法虽然运行简单快捷,但是需要手动选取区域,存在人为主观误差;何凯明[8]通过统计大量的无雾图像,发现在绝大部分非天空区域,至少有一个颜色通道的像素值较低并以此提出了暗通道先验理论,通过软抠图法得到了优化的透射图,此方法能够消除大部分图像的雾霾,但是对于存在大片天空区域的图像,容易出现光晕现象造成去雾图像颜色失真.
本文算法通过运用Stokes矢量公式计算图像的偏振信息,将其映射到HSI颜色空间提高目标细节特征,再转换到RGB空间,通过暗通道先验原理求取透射图,用导向滤波优化透射图;考虑了图像中因场景深度对偏振引起的变化,对图像中每一点像素值进行参数重构运算,避免了因选取图像中某一区域的大气光偏振度代替整幅图像的大气光偏振度而引起的误差;通过形态学对图像重建处理后求取局部极大值来代替无穷远处大气光值.
1 HSI颜色空间与偏振信息
HSI模型符合人类对于描述物体和解释颜色的方式,所以在处理彩色图像方面可以得到较好的结果.偏振光是一种光矢量振动方向不变并且具有某种变化规则的光,其所含的偏振信息不会因为光的吸收和散射而衰减,能够保留较完整的目标信息.为描述偏振信息,可以采用Stokes矢量(I、Q、U、V),其中I代表总光强,Q代表X轴方向上的偏振光分量,U代表45°方向的偏振光分量,V代表圆偏振光,因为自然光中的圆偏振信息微乎其微,所以通常假设V= 0.
1.1 图像偏振信息
描述偏振信息需要偏振度图像DOP和偏振角图像AOP,通过偏振度图像描述光强度的比例,通过偏振角图像描述偏振光振动方向和参考方向之间的夹角.
(1)
(2)
式(1)和式(2)中的Stokes矢量参数I、Q、U,可以通过式(3)获取.
I(αi)=(I+Qcos 2αi+Usin 2αi)/2
(3)
式中αi是指偏振片偏振方向与标准方向之间的夹角,通过获取三幅不同角度的偏振图像就可以求解出Stokes矢量参量I、Q、U,也可以求解处于不同偏振角度时的光强图像I(αi).本文采用0°,60°,120°三个方向的偏振图像.
1.2 偏振信息映射到HSI颜色空间
通过式(1)~式(3)求出总强度图像I、偏振度图像DOP和偏振角图像AOP.HSI颜色空间模型可以消除图像彩色信息携带的强度分量的影响,是一种彩色图像处理算法理想的描述工具,对人的视觉来说更加直观.为了增强偏振图像中的目标特征信息,将获取的偏振信息强度图像I、偏振度图像DOP和偏振角图像AOP映射到HSI空间模型.其中具体的映射关系[5]如下:

(4)

(5)

(6)
1.3 HSI空间与RGB空间的转换
现有很多的彩色模型如RGB模型、CMY和CMYK彩色模型等[6]虽然对于硬件的实现都很理想,但是并不能很好描绘人眼所观察的颜色.而HSI彩色模型是通过色调、亮度和饱和度来描述目标,色调H类似于RGB模型中的颜色种类,亮度I与色彩信息不相关,却是人类对于彩色感觉的重要参数,饱和度S描绘了物体颜色的浓度.将偏振信息映射在HSI模型上可以提高目标的细节特征,因为需要通过Matlab离线处理图像,所以最终需要转换到RGB空间上进行图像运算.
2 偏振图像去雾模型
产生雾霾的主要原因有两点,一是目标反射光在雾霾天气情况下因为大气中的悬浮粒子产生的吸收和散射作用,使目标反射光能量逐渐衰减,探测器接收到的图像亮度变暗、对比度降低;另一点是像太阳光等环境光因为大气中的散射介质产生背景光,而通常背景光强度大于目标光,导致探测器接收到的图像模糊不清.根据Mie散射理论可知被广泛认可的大气散射模型图[7]如图1所示.
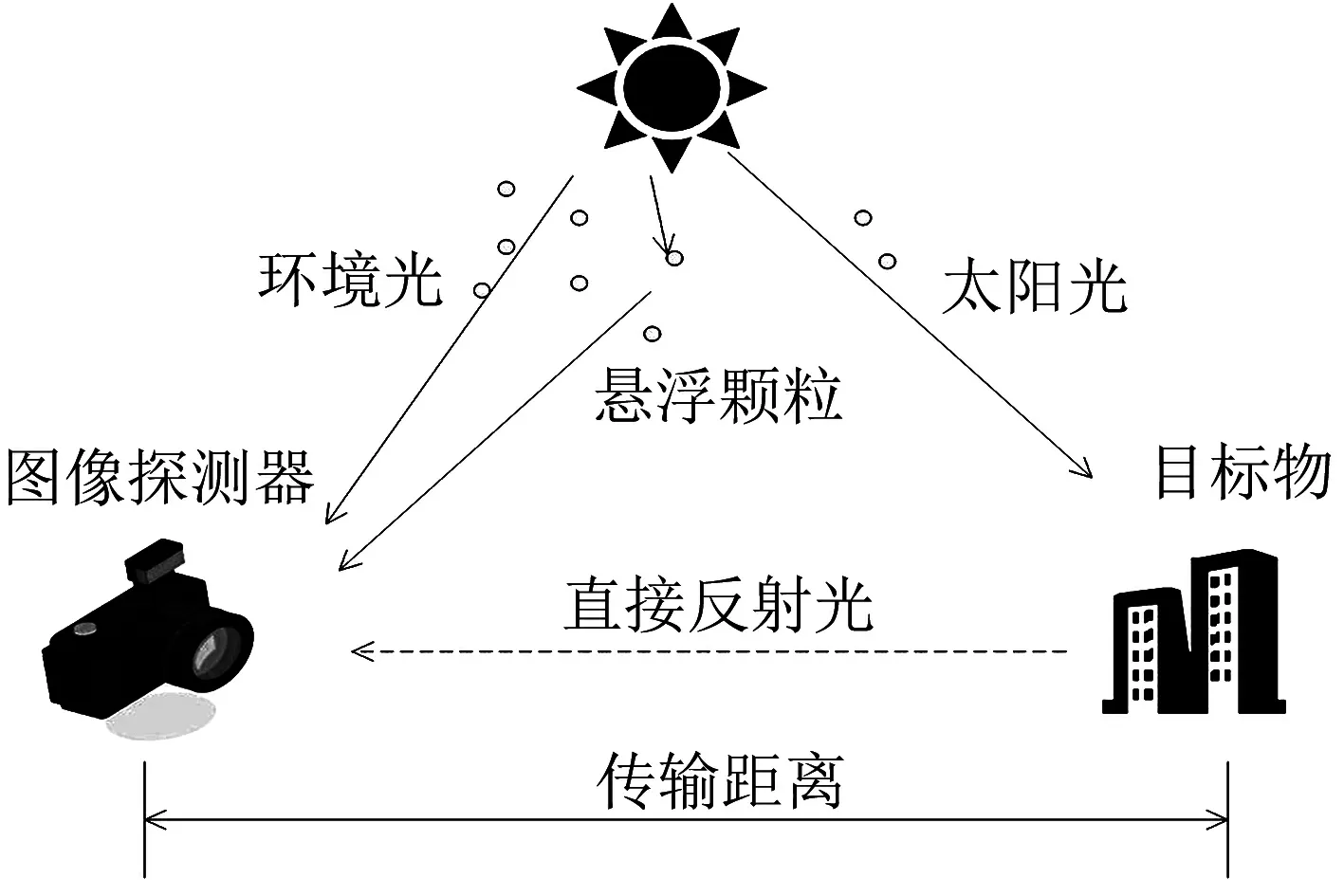
图1 大气散射模型
Schechner在大气散射模型的基础上,通过光的偏振原理改进了图像去雾模型如下:
I(x,y)=D(x,y)+A(x,y)
(7)
式中:D(x,y)指的是目标观测点的场景光强,通过大气散射模型可知D(x,y)=L(x,y)t(x,y),其中L(x,y)是待复原的图像,t(x,y)是传输图,式(7)中A(x,y)是大气光强图像,由式(8)组成:
A(x,y)=A∞(1-t(x,y))
(8)
式中,A∞是指无穷远处区域的大气光数值.
根据文献[4]可知探测器接收到的图像强度可以分解为平行和垂直入射面的两个偏振分量Amax(x,y)和Imin(x,y),同样大气光强A也可以分解为平行和垂直入射面的两个偏振分量Amax(x,y)和Amin(x,y).通过式(1)可知最大光强和最小图像为:
Imax(x,y)=D(x,y)/2+Amax(x,y)
(9)
Imin(x,y)=D(x,y)/2+Amin(x,y)
(10)
根据偏振度的定义可知偏振度图像和大气光偏振度图像为:
(11)
(12)
通过式(7)~式(12)可知偏振去雾表达式为:
(13)
由式(13)可知只需要求解图像总强度I、图像偏振度DOP、大气光图像偏振度PA和无穷远处大气光强四个参量即可去除雾霾对图像造成的影响,提升图像对比度,增强场景目标物的细节信息.
2.1 暗原色先验与传输图优化计算
暗原色先验原理[8]是何凯明通过测试数千幅户外无雾图像验证了其合理性,通过计算这些图像可知,图像的R、G、B三个通道之中必然存在一个通道的像素值很低.如式(14)所示:
(14)
式中,Jc(y)是图像J的其中一个通道,Ω(x)是以像素值x为中心的一个方形区域,通过式(14)可知Jdark(x)的像素值都相对较低,所以Jdark(x)为图像J的暗原色图像.根据大气散射模型原理可知复原图像可由式(15)表示:
J(x)=(I(x)-A(x))/t(x)+A(x)
(15)
对式(15)两边同除大气光图像A后进行局部最小值滤波操作可以得到透射率图t(x),见式(16):
(16)
通过式(16)求取的透射图存在块效应,本文使用导向滤波[9]进行透射图的优化.
2.2 求取无穷远处大气光强
Li等人[10]认为灰度图像中像素值的分布大致符合正态分布曲线,通过求取灰度图像像素值的均值与方差,运用阈值对正太分布曲线中的像素值迭代筛选出无穷远处的点,然而一旦遇到图像中有大量白色区域时(见图2(a)),仍然无法准确估计无穷远处的区域.而本文通过数学形态学的知识处理偏振图像,因为无穷远处区域的像素值要大于附近的近景区域的像素值,所以对图像进行形态学重建后求取其局部极大值,通过图2(b)可以看出,本文算法能够很好地避免白色高楼带来的影响并且能够自动筛选出无穷远处区域,通过对筛选出的区域像素值求取平均像素值来代替无穷远处的大气光强值.

(a) LI的方法

(b) 本文的方法图2 求取无穷远处大气光强方法对比图
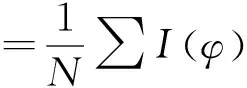
(17)
2.3 估算大气光偏振度信息
传统的偏振去雾模型求取大气光偏振度都是通过选取最大最小光强图像[11]上的无穷远处区域作为大气光的代替值,从而计算出大气光的偏振度值,但是将大气光偏振度当作一个全局不变量忽略了现实环境中场景深度对于偏振引起的变化,将其当作一个常量与实际情况存在误差,并且在之后的去雾运算中误差将逐渐增大造成复原结果失真.本文通过将偏振信息映射到HSI颜色空间增强图像的目标细节特征,根据暗通道先验原理运用导向滤波求取优化后的透射率图,根据式(8)可知优化后的透射率图和基于形态学求取的无穷远处大气光强值可以得到大气光强A.通过式(9)~(12)可以求取的全局变量参数大气光偏振度PA:
(18)
通过式(18)得到全局变量的大气光偏振度图像,解决了因为将大气光偏振度当成全局不变量而产生的误差,使复原效果更加符合现实场景.
2.4 通过归一化互信息改进大气光偏振度
通过偏振图像复原机理可知大气光偏振度的估计精度和大气光息息相关,当大气光偏振度估计精度有误时会造成复原图像目标细节丢失,场景光强D和大气光强A反应图像的不同信息,所以精确的PA应该使D和A的关系越小越好.本文通过归一化互信息NMI[12]来衡量图像之间的关系:
(19)
式(19)中pi(•)是图像的灰度级i的分布概率,pi,j(A,D)是图像A和D的联合概率分布,NMI(A,D)越大说明两者关联越大,所以精确的PAoptimal应为获得最小NMI时所对应的偏振度信息值:
PAoptimal=arg minNMI(A,D)
(20)
3 实验结果与分析
本文通过实验室所研制的三通道偏振相机获取雾霾天气情况下的图片,实验所使用的图片均为实际拍摄后经过配准处理运算后所获取,为了验证本文去雾算法的有效性,引进了信息熵、平均梯度和灰度方差三个客观指标进行评价,这三个值越大,证明图像质量越好.这里分别将本文算法与Schechner的算法和暗通道先验算法进行对比.
Schechner的算法通过手动旋转偏振片获取平行和垂直入射平面的正交偏振图像,手动选取天空区域计算无穷远处大气光强值,这种方法存在着人为主观性的误差且增加了人机交互性的烦琐;本文通过三通道偏振相机获取不同角度的偏振图像,通过形态学重建图像求取局部极大值可以自主选取无穷远处的区域.从图3中可以看出相对于Schechner的算法,本文提出的算法如图3(f)在远处的大楼可以清晰看到窗户的轮廓,近处楼房上的字更为清晰,整体图像复原效果要优于Schechner的算法.

(a) 原图

(b) Schechner算法

(c)本文算法

(d) 原图

(e) Schechner算法

(f) 本文算法图3 Schechner算法与本文算法的去雾图像对比
通过表1可知两组雾天图像通过Schechner的算法和本文算法分别去雾后,质量评价指标的量化结果相对于雾天图像均有提高,粗体数字代表效果最优,从表1可以看出本文算法在信息熵、平均梯度和灰度方差方面均优于Schechner算法.

表1 Schechner算法与本文算法图像质量评价表
从图4(b)和图4(e)中可以看出何凯明的暗通道算法对拥有大片天空区域的图片处理上容易出现颜色失真的情况,尤其是天空区域光晕情况十分严重.本文的算法能够在去除雾霾影响的情况下,保证天空区域不会出现颜色失真的情况.图4(c)和图4(f)是通过本文算法进行去雾后的结果,可以观察到图像中的白色教学楼去雾效果明显,整体轮廓清晰,天空区域符合现实情况,不会出现严重的光晕现象.

(a) 原图

(b) 暗通道算法

(c)本文算法

(d) 原图

(e) 暗通道算法

(f) 本文算法图4 暗通道先验算法与本文算法的去雾图像对比
从表2可以看出本文提出的算法在信息熵、平均梯度和灰度方差要远高于雾霾图像;图4(c)在信息熵方面略低于暗通道算法,因为信息熵反映了图像包含的细节程度,从图4(c)可以看出本文算法虽然对于场景中远处细节恢复明显,远处的教学楼轮廓复原明显,图像整体对比度有所加强.但是左下角的树木却因为距离探测器过近,在去雾过程中存在部分细节丢失,所以导致图像中信息量减少,数值略低,但是图像整体复原情况要优于暗通道算法.

表2 暗通道算法与本文算法图像质量评价表
4 结论
本文算法针对雾霾天气图像质量下降的情况,提出一种全局参数估计的颜色空间转换偏振去雾算法.通过将偏振信息映射在HSI空间上增强目标细节特征,求取优化的透射图,重构大气光偏振度图像中每一点的像素值,通过形态学重建雾霾图像求取其局部极大值,自动求取无穷远处大气光值.相对于Schechner的算法,本文不需要手动选取天空区域,避免了因为人机交互而造成的精度误差;相对于暗通道算法,本文算法解决了大片天空区域出现光晕、颜色失真等问题.通过信息熵、平均梯度和灰度方差三个评价指标可以看出本文算法有着较好的去雾效果,恢复了更多的目标细节特征,为了后续进行实时视频去雾奠定了良好的基础.

