基于小波分析的转辙机声信号去噪研究
姜琦,冯庆胜
(大连交通大学 自动化与电气工程学院,辽宁 大连 116028)
转辙机作为重要的铁路信号基础设备之一,因其长期处于室外极易产生故障,通过其动作声信号分析可实现结构损伤检测,探究好的声信号降噪方法对后续的设备故障分析有非常重要的作用与意义[1-2].
目前对转辙机故障信号有多种采集手段,夏平[3]用超声波检测技术采集超声缺陷回波信号进行分析.荆戈[4]用红外热像仪采集转辙机表面红外辐射进行分析.仲祎敏[5]用视频监测系统采集图像信号进行分析.以上方法或检测方式复杂,或受天气干扰大或检测不全面,在实际检测中皆有不足之处.而声音信号具有非接触、易于采集等优点,且转辙机运动过程中产生的声音信号包含了可分析的故障信息.应用小波分析对声音信号的去噪处理方法也较为成熟,赵月静[6]采用改进阈值小波分析对机床冲孔声音信号进行去噪处理,取得良好效果.郭凤霞[7]采用小波变换理论通过对比试验得到适用于回波信号的最佳分解层数和阈值,实现了声雷达回波信号中杂波和噪声的去除.
本文使用小波阈值去噪法,对处于不同工作环境的转辙机声音信号进行处理, 通过MATLAB软件计算对比均方根误差和信噪比,并结合波形图分析得到最佳去噪方法.
1 小波阈值去噪概述
小波变换是一种优于傅里叶变换的分析方法, 它既有短时傅里叶变换的局部化优势,又具有可随频率改变的时频窗口,该方法能够在高频处时间细分,低频处频率细分,因而是一种比傅里叶变换更有效的降噪方法.由于在实际应用中信号多使用数字处理模式,因此需将信号进行离散小波变换,以获得适合计算机软件处理的离散信号,并最大程度上消除和降低冗余度.
在进行离散小波变换时,通常把尺度a和偏移b取作幂级数的形式:
假设a0>1对应的离散小波为:
(1)
对于信号x(t)的离散小波变换系数可表示为:
(2)
对于信号x(t)的离散小波重构公式为:
(3)
其中,c是一个与原始信号无关的常数.
小波变换的一个重要应用就是对一维信号进行消噪处理,一个含噪声的一维信号模型可表示为:
s(n)=f(n)+σ·e(n)
(4)
其中,n=0,1,2,…,N-1,s(n)为含噪信号,f(n)为原始信号,σ为噪声强度,e(n)为噪声信号.
在对实际信号处理时可发现,噪声信号或故障信号常处在高频段且非平稳,而有用信号则常处于低频段并较平稳.这样的特性恰恰为运用小波分析进行信号去噪的方法提供了前提条件.当对含噪信号进行尺度分解后,应用门限阈值形式(阈值去噪法)对含噪声的高频小波系数行处理,然后将处理后的小波系数进行重构便可完成消噪.
信号的消噪处理过程如图1所示,利用小波进行消噪处理分为如下四个步骤:

图1 小波消噪处理过程图
(1)对含噪信号进行预处理,以便进行后期处理;
(2)信号的小波分解,根据实验观察与分析,确定利于信号分解的小波函数和分解层数;
(3)高频系数的选择与量化,对每一层高频系数选择一个阈值,并进行阈值量化处理;
(4)信号的重构,也是对第N层的小波分解低频系数与第一层至第N层经量化处理后的高频系数的重构.
根据有用信号与噪声信号在频域中的分布特点,对信号进行小波分解时更为重视对低频部分的处理.由于在低频部分中包含信号的基本特征,高频部分对应信号的细节,与噪声有关.因此,小波分解是对信号的低频部分多次分解,对高频部分不做二次分解的方法.对信号S的小波分解树如图2所示.

图2 小波分解树
图2将信号进行了三层分解,其公式可表达为:S=A1+D1=A2+D2+D1=A3+D3+D2+D1.在原则上可对信号低频部分无限分解下去,即把图中信号低频部分A3分解为低频A4与高频D4,依此类推.然而在实际分析过程中,不可对信号的分解层数随意选择,需通过观察波形图和准确的评判标准来确定最佳分解层数.从图2可以看出,对低频部分每一次分解,都会使频率的分解率逐步变高,过高的分解层数会使获得的信号失真,过低的分解层数无法将噪声有效消去.小波基类型的选取也是同理,与所分析信号波形,性质相差较大的小波基无法有效对信号进行处理,同样需经实验对比确定最优小波基类型.
2 默认阈值的小波去噪参数选取
根据小波消噪处理步骤2可知,当运用小波阈值去噪法对转辙机动作声音信号进行消噪处理时,需先确定合适的分解层数和小波基类型.因此,本文以信噪比及均方根误差作为评判标准,以更精确的方式选取有效的去噪参数.
均方根误差(Root Mean Squared Error,RMSE)计算出的数值代表观测值与真实值之间的偏差.用其判断同一转辙机动作声音信号在不同的参数选择下产生的去噪信号与原信号的相似程度.其公式为:
(5)
其中,m为样本个数,yi为原信号真实值,h(xi)为与原信号对应的消噪信号观测值.
信噪比(SIGNAL NOISE RATIO,SNR or S/N)在不同的应用领域内有不同的表达方式,为衡量去噪后转辙机动作声音信号效果的优劣,其表达式为原信号能量与去噪信号和原信号差值的能量之比.其公式为:
(6)
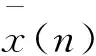
2.1 分解层数选取
为选择对转辙机动作声音信号去噪的最佳分解层数,需保持其他变量不变,即确定小波基类型和阈值选择标准.先使用具代表性的Daubechies小波系db5,以及常用的gbl全局阈值标准.全局阈值的计算公式为:
(7)
其中,σ为噪声标准差,M,N为信号尺度.
使用MATLAB计算在不同分解层数下的SNR和RMSE值,确定适合的分解层数.计算结果如表1.

表1 四种分解层数降噪效果对比
由表中数值可观察出,当转辙机动作声音信号分解层数为1层时,得到的信噪比SNR最大,均方根误差RMSE最小.该结果说明最佳分解层数为1层,同时也验证了小波变化的多分辨率分析理论,即高层次分解出的小波系数来源上一层的低频部分,而信号的主要成分处于低频部分.因此越多的分解层数,去掉的低频成分越多,失真度也越高,反而不利于对信号的分析.
2.2 小波基类型选取
选择最佳小波基并没有统一的标准,通常是按照小波基函数的性质、待检测信号的特征及信号处理的目的等,凭经验选择最佳小波基[8].在实际选择小波基时,可通过观察信号的形状,并结合计算结果,分析比较选出最佳小波基.
由图3与图4可看出,Daubechies小波系中有与转辙机动作声音信号形状较为相似的小波类型,因而使用该小波系类型进一步实验.

图3 原始信号时域图

图4 db8小波基时域图
全局阈值gbl和分层阈值lvd是两种常用的阈值选择标准.全局阈值是指对各层小波系数或同层内在方向上有差异的小波系数选择相同的阈值;分层阈值是对不同层不同方向的小波系数选取不同的阈值.但由于该转辙机动作声音信号的最佳分解层数为1层,因此使用全局阈值和分层阈值的结果并无差别.
根据表2可知,当选择小波基由db1到db8时,所计算出的信噪比逐步增大,均方值误差逐步减小.当选择小波基由db8到db9时,均方值误差不再减小,且信噪比出现了下降趋势.该结果证明db8为最佳小波基类型.

表2 不同小波基类型的降噪结果对比
3 默认阈值去噪仿真结果
在表1与表2分别确定了本转辙机动作声音信号去噪的最佳分解层数1层与小波基类型db8后,使用软硬两种阈值处理方式对全局阈值的小波系数进行处理.
硬阈值处理是把算得的阈值与信号分解所得的小波系数绝对值进行比较,将绝对值大于阈值的点保持不变;小于或等于阈值的点取0.
其中硬阈值函数为:

(8)
该函数图像如图5所示,图中δ为阈值,x为小波系数.

图5 硬阈值函数
软阈值处理同样是把算得的阈值与信号分解所得的小波系数绝对值进行比较,不同的是将绝对值大于阈值的点变为该点值与阈值的差;将绝对值小于或等于阈值的点取0.
软阈值函数为:

(9)
该函数图像如图6所示.图中,δ为阈值,x为小波系数.
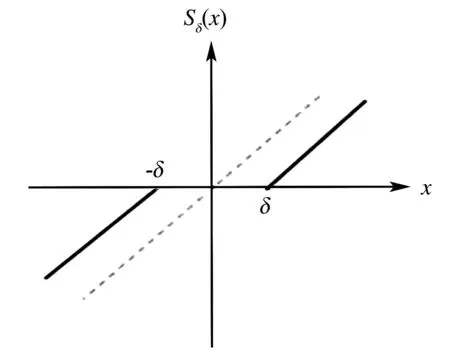
图6 软阈值函数
仿真去噪后的信号波形图如图7和图8.

图7 db8的硬阈值去噪信号

图8 db8的软阈值去噪信号
计算两种降噪方式的信噪比与均方根误差对比结果如表3所示.

表3 两种降噪方式对比
可以看出,经多种方法去噪后所得的信号在时域波形图上与原始信号非常相似,但是经过计算信噪比和均方根误差,可以清晰地看到其中差别之处.在软硬阈值处理方式对比中,小波系数采用硬阈值时得到的信噪比大于采用软阈值时得到的信噪比,采用硬阈值时得到的均方根误差小于采用软阈值时得到的均方根误差.说明经硬阈值处理的结果在数值上优于软阈值.但表格中软硬阈值处理得到的信噪比皆不高,为此需进一步研究提出改进方法.
4 指定阈值选取的小波去噪分析
除全局阈值去噪法外,还有四种可用以分析的阈值去噪方法.
Stein无偏估计阈值(rigrsure):一种以Stein无偏似然估计原理实现的阈值获取方法,是将最小风险量对应的小波变换系数作为阈值,且具有自适应性,其具体算法为:
(1)将每一层的小波系数(设其长度为n)平方之后,由小到大进行排列,得到新的向量P.
(2)将向量P中的每个元素按下式计算风险向量:
(10)
(3)由风险值Rk对应的小波系数平方Pk以下式求得阈值δ为:
(11)
固定式阈值(sqtwolog):设由小波系数构成的向量长度为n,则阈值计算公式为:
(12)
启发式阈值(heursure):它是一种无偏估计阈值与固定式阈值二者相结合的阈值获取方法.当信噪比很大时,采用无偏估计阈值法;当信噪比很小时,采用固定阈值法.具体是判断两个变量Eta和Crit的大小,它们的表达式分别为:
(13)
(14)
其中,n为向量的长度,wj为离散信号.
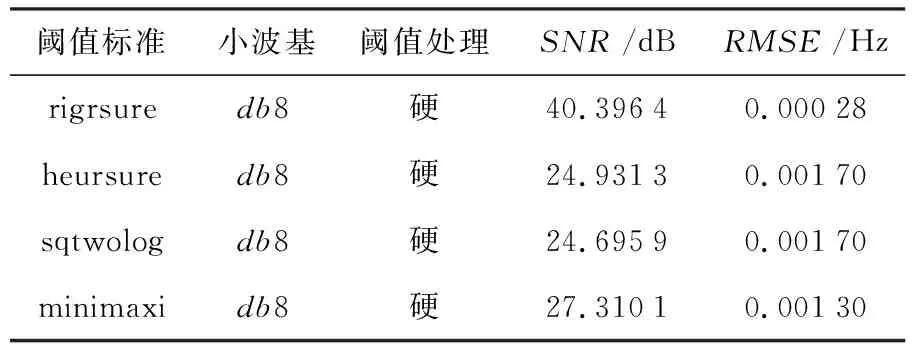
评判标准是当Eta 极大极小值阈值(minimaxi):也可作为一种固定阈值方法.其原理是让估计的最大风险最小化.该阈值计算公式为: (15) 上述四种阈值中含有的噪声是标准差(小波域)为1的高斯白噪声,所以在对信号去噪时,实际阈值应为δ·σ,其中σ为噪声的标准差.由于一般认为最小尺度上的小波系数大部分由噪声引起,因此噪声标准差为: (16) 其中,Mx是含噪信号最小尺度上对应的小波系数绝对值向量的中位数. 现选定小波基类型为db8,小波系数采用硬阈值,分别计算四种方法在不同分解层数下的SNR和RMSE,其折线图如图9与图10所示. 图9 消噪信号信噪比 图10 消噪信号均方根误差 图中四种阈值方式的最优数据,如表4所示. 表4 四种降噪方法最优值 从表4可看出,在采用以上四种阈值去噪法后,信噪比较全局阈值方法整体出现了至少一倍的提高,均方根误差也整体下降.其中,采用Stein无偏估计阈值的去噪效果最为突出. 本文完成了转辙机动作声音信号的去噪方法研究,通过实验确定最佳分解层数与小波基类型.在此基础上,选取不同阈值获取标准,通过分析不同标准下信号去噪后的波形图,并结合信噪比和均方根误差计算数值,以更加精确的方式,对降噪后信号的效果进行分析和评价.由结果可知,在选用db8小波基类型、1层分解、阈值硬处理下,Stein无偏估计阈值法去噪时可使信噪比高于40 dB.这证明小波分析可有效消除转辙机声音信号中的环境噪声,为转辙机的动作声信号分析及其故障处理提供了参考.

5 结论

