提高解题能力 落实核心素养
——浅谈一节高三复习课的教学感悟
◎李成坤(嘉兴市第三中学,浙江 嘉兴 314051)
一、课堂呈现
笔者在一节高三数学复习“绝对值不等式的解法”教学过程中,引导学生对下列例题进行了解法探究:
2020年高考全国2卷(理科数学)第23题第(1)问:
已知函数f(x)=|x-a2|+|x-2a+1|.当a=2时,求不等式f(x)≥4的解集.
笔者先让学生独立思考这个问题,很快就有一名同学给出一种解答方法.
二、解法探究
当a=2时,f(x)=|x-4|+|x-3|,即求不等式|x-4|+|x-3|≥4的解集.
生1:(方法一)利用函数y=|x-4|+|x-3|的零点3和4,分段讨论去绝对值.
(1)当x≤3时,

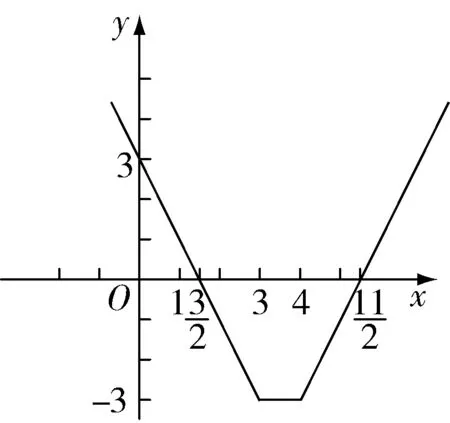
(2)当3 (3)当x≥4时, 教师点评:方法一利用函数y=|x-4|+|x-3|的零点3和4,将数轴分为三个区间,进行分段讨论去绝对值,体现了分类讨论的思想. 生2:(方法二)不等式f(x)≥4的解集等价于求解不等式f(x)-4≥0. 设函数 教师点评:方法二是通过构造函数,利用函数的图像直观求解,体现了函数与方程的思想. 生3:前两种解法都需要先分类去绝对值再进行求解,其实第一问可以不用分类讨论进行求解,解法如下: 方法三:如图所示 此时,教室响起了掌声! 教师点评:方法三利用绝对值的几何意义进行求解,体现了数形结合的思想,方法巧妙,思维深刻. 这时,笔者问学生:“同学们,此题还有其他的解法吗?”等了片刻,班级还是没有学生举手回答,笔者开始讲解另外两种解法. 教师:由绝对值不等式|a±b|≤|a|+|b|(a,b∈R)可知, |x-4|+|x-3|≥4⟺|(x-4)+(x-3)|≥4或|(x-4)-(x-3)|≥4. 方法四:由|x-4|+|x-3|≥4可得, |(x-4)+(x-3)|≥4或|(x-4)-(x-3)|≥4. 解得,|2x-7|≥4或|-1|≥4, 教师点评:方法四利用绝对值不等式|a±b|≤|a|+|b|(a,b∈R)对所求问题进行等价转化,很巧妙地把两个绝对值问题转化成一个绝对值问题进行求解,极大地简化了运算,避免了烦琐的分类讨论,此方法体现了等价转化思想的重要性. 接着教师再次引导学生对方法四进行归纳总结,得到一般性结论: |f(x)|+|g(x)|≥h(x)⟺|f(x)+g(x)|≥h(x)或|f(x)-g(x)|≥h(x). 教师:根据绝对值的定义可知,该不等式的含义是数轴上的点x到两定点(3,0)和(4,0)的距离之和大于等于4.这也恰好符合椭圆的定义,故可用椭圆的知识来解释该不等式. 方法五:设椭圆的长轴在x轴上,两个焦点分别为(3,0)和(4,0),定长为4,椭圆与长轴的交点的横坐标为x1与x2.由椭圆的定义可知,x1,x2恰好是x轴上分别到3和4的距离等于定长4的点(如图所示), 因此,x轴上到(3,0)和(4,0)的距离大于定长4的点必定落在这两根之外, 教师点评:方法五是构造椭圆模型,利用椭圆的概念进行求解,避免了分类讨论的烦琐. 为巩固上述解绝对值不等式的方法,课堂上笔者让学生做了以下练习题目: 练习1:求解不等式|x-1|+|x-2|≥3. 练习3:求解不等式|x+1|-|2x-3|>1. 笔者让三名学生到黑板上完成这三道练习题,并让他们讲述解法…… 教师点评:这三道题,大多数学生用到了方法一、二或者三中的某一种,并且答案正确,大多数学生做得很好.全班只有三名学生选用了方法四进行求解,没有一名学生用方法五求解,还有两名学生没有做出此题,个别学生有答案计算错的. 接着,笔者针对这三道题又给学生做了解法上的引导和讲解…… 教师:请同学们自我总结一下,这节课你都有哪些收获? 学生1:学会了求解含两个绝对值不等式的前三种解法,后面两种解法还不是很清楚,不太会用. 学生2:学会了求解含两个绝对值不等式的前四种解法,后面一种解法听懂了,但是还不太熟悉,不会用来求解.同时体会了函数与方程、数形结合、分类讨论、等价转化等重要的数学思想方法,收获颇丰. 学生3:学会了多种求解绝对值不等式的方法,方法五令我很惊奇,没想到绝对值不等式还能和解析几何中的椭圆建立联系,让我深深地感受到代数和几何是紧密联系在一起的,以后思考问题时要学会从多角度进行思考. 教师:同学们回答得很好.我们一起再总结一下:这节课我们复习了“绝对值不等式的解法”,教学过程主要是围绕|x-4|+|x-3|≥4解法的探究展开的,其中方法一利用函数“零点分段法”求解,体现了分类讨论的思想;方法二是通过构造函数,利用函数图像直观求解,体现了函数与方程的思想;方法三利用绝对值的几何意义进行求解,体现了数形结合的思想.这三种方法都是求解形如|x-a|+|x-b|≥c和|x-a|+|x-b|≤c(a,b,c∈R)类型不等式的通用方法.方法四利用绝对值不等式|a±b|≤|a|+|b|(a,b∈R)进行等价转化,体现了等价转化的思想,同时得到一般性的结论:|f(x)|+|g(x)|≥h(x)⟺|f(x)+g(x)|≥h(x)或|f(x)-g(x)|≥h(x);方法五是构造椭圆模型,利用椭圆的概念进行求解,属于巧解,拓宽了大家的解题思路和思考问题的视角.希望同学们仔细体会这些解题方法,更重要的是细细品味蕴含其中的数学思想,并学以致用. 俗话说:“一只手五个手指各有长短.”一个班级的学生,由于知识基础、学习能力及学生自身的智力因素等不尽相同,学生的学习客观上存在着个体差异,导致班级学生学习水平不等、成绩有差异.因此,教师在教学过程中要关注学生的个体差异,满足不同学生的学习需求,尽量使每一名学生都能获得成功的喜悦,促进每一名学生全面而富有个性的发展.充分发挥一题多解在建立知识联系、灵活应用知识、实现不同表现形式的相互转化等方面的作用,通过多角度、全方位解题,开阔学生的视野,拓展学生的思维,帮助不同程度的学生运用适合自己的解题方法去解题,能很好的满足不同层次学生的需求. 新课程理念强调学生是学习和发展的主体,要重视培养学生主动探究、团结合作、勇于创新的精神.高三数学复习课堂教学中,教师既要传授学生获取知识的方法,又要给学生提供自主探究的时间和空间,鼓励学生积极自主地探究数学问题.这也就要求教师在教学中要精选题目,使得每一道题目都要有它的训练目标,并使这些题目能够组合成一个有机体,从而实现这节课的总的教学目标.教师还要引导学生对一题多解的题目进行解法的提炼和对比,“授人以鱼,不如授人以渔”.一题多解的引用主要是要让学生细细体会每一种解题方法、技巧及蕴含其中的数学思想,对比各种解法的优劣,根据自身的基础和理解能力,选择适合自己的解法,从而达到提升学生解题能力的最终目的. “知识”是基础,“方法”是手段,“思想”是灵魂.教师要对学生的解题过程进行引导与指导,在探究解决问题的方法过程中要进一步渗透数学思想,使学生体会到解题方法中所蕴含的重要数学思想方法(如函数与方程、数形结合、分类讨论、等价转化等),真正感受数学思想贯穿整个解题过程,是解题的灵魂.在教学过程中,教师要只有提高学生对数学思想方法的认识和运用,才能真正有效地落实学生的核心素养.
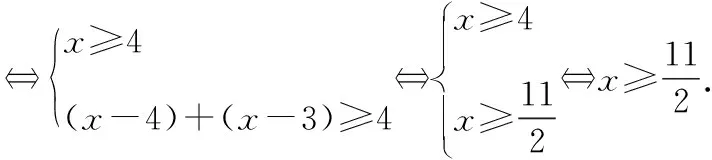
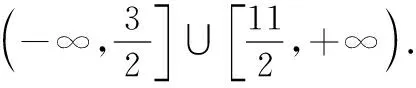

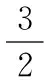






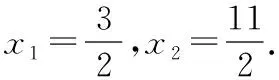
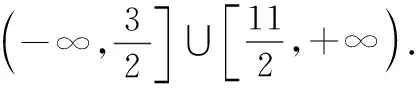
三、解法运用
四、课堂总结
五、教学启示
(一)一题多解,满足不同学生的需求
(二)提炼总结,提升学生的解题能力
(三)渗透思想,落实学生的核心素养

