基于Matlab激光谐振腔中激光模式形成机理研究

张亚妮， 薛 佳， 宋卓颖， 苗 挺， 姚一铭， 武柯欣， 陈敬梓

(陕西科技大学 文理学院， 陕西 西安 710021)

0 引言

激光(Laser，Light Amplification by Stimulated Emission of Radiation)由于具有良好的单色性、方向性、相干性以及超高亮度和超短脉冲等性质而被广泛应用于各种领域，如生物医学[1]、通信以及受控核聚变等.激光作为测距光源,因其方向性好、功率大,能够精确地测量极远距离；激光因其良好的相干性,在通信领域获得了广泛应用；激光能量的可控性使其在受控核聚变的研究中占据着不可忽视的地位.1960年世界上第一台激光器——红宝石激光器的成功研制和半导体技术的快速发展,使得半导体激光器得到快速发展及应用.最典型的半导体激光器——半导体激光二极管的发明让激光应用得以迅速普及,各类信息扫描、光纤通信、激光测距、激光雷达、激光唱片、激光指示等已与半导体激光二极管密不可分.在国防领域,半导体激光器作为新一代小型化、轻量化的激光载荷光源[2],也被广泛装备到车载或机载等机动性强的作战平台.

激光的产生需要有三个必备条件,即：具有适当能级结构的激光工作物质；使工作物质发出激光的激励源(泵浦源)[3]以及光学谐振腔.前二者为实现集居数反转进而实现光放大奠定了物质基础.然而,光放大后受激辐射呈现的随机性并不能获得相位、频率、振动方向和传播方向均完全相同的激光束.因此,要获得真正意义上的激光,关键在于光学谐振腔的选模作用[4].

光束质量是激光器的重要指标,度量激光束的聚焦程度[5].影响光束质量的主要因素是光学谐振腔的设计与选择,光学谐振腔的形状与设计参数对激光振荡器的模式产生和选择具有无可替代的作用,激光模式选择又是提高光束质量的有效途径.随着对高功率、高能量、高光束质量(高亮度)激光器应用需求的快速增长,通过光学谐振腔的优化设计及激光合束技术,实现千瓦、万瓦乃至更高功率高光束质量激光输出是激光武器发展的迫切需要.

光学谐振腔的主要作用是提供正反馈能量以及选择光束的频率和方向.在工作物质两端恰当安装两个反射镜片,构成开放式光学谐振腔,可从各种可能光信号中选取特定光信号进行放大.谐振腔对激光束的形成影响重大[6],谐振腔使受激辐射集中于特定方向输出,使光束呈现很好的方向性；谐振腔的稳定输出强度和选频作用能够提高输出光束的单色性.谐振腔内可能存在的激光模式按照光束方向和频率分为横模与纵模[7].本征模式受谐振腔的影响是由两个反射镜的自身性质以及间距来决定的,不同类型的谐振腔具有不同的模式选择特性和模式结构.因此,谐振腔中激光模式的优化对激光器性能及激光光束的改善具有重要作用[8].激光腔模式经典理论仅给出了部分简单腔的解析解.激光技术的发展致使各种复杂的谐振腔型精彩纷呈,解析解无法满足谐振腔的求解需求,需要采用数值仿真方法实现谐振腔的模式选择.Matlab强大的数据处理和图像拟合功能可以直观地展示谐振腔的自再现模[9],为复杂谐振腔的模式优化奠定了重要基础.本文基于Matlab数值分析软件,通过对各种复杂谐振腔的数值求解,模拟得到不同谐振腔内的光场模式与菲涅耳数之间的分布关系,绘制出振幅分布图、模场分布图及模场花样分布图,通过各种谐振腔模式分布图样的对比分析,为通过模式选择实现光束质量优化奠定基础[10].

1 光学谐振腔结构及仿真模型

在光学谐振腔的模式分析中,菲涅耳数有着重要的调节作用.菲涅耳数是表征衍射损耗大小的物理量,菲涅尔数越大,衍射损耗越小.一般谐振腔的菲涅尔数较大时,低阶模式和高阶模式的衍射损耗非常接近,高阶模在有限的迭代次数下不能有效地消除；而谐振腔的菲涅耳数较小时,高阶模具有更高的彩色损耗,能够有效地抑制高阶模振荡.通过选用波长为632.8nm的氦氖激光器,设计三种谐振腔型：平行平面腔、圆形共焦腔、方形共焦腔.运用Matlab数值分析软件,通过调节腔长,改变菲涅尔数F,获得在不同菲涅尔数下的振幅和相位分布[11]、自再现模平面图、三维模场图及模场分布花样,最后针对不同迭代次数得到的结果进行分析,获得形成最佳激光模式输出的谐振腔型和参数.

1.1 平行平面腔[12]

平行平面腔分为一维条形腔和二维矩形腔.

(1)一维条形腔

条形腔是一种一维理想模型,即一个方向有限长,而另一个方向上无限延伸的腔形,其只在长度有限的方向上发生衍射现象,其迭代公式为一维菲涅尔-基尔霍夫衍射积分：

(1)

其求解方法为将条形腔左镜面沿着(-a,a)之间划分N-1等分,则有N个点,每个区间为2a/(N-1).右镜面上每一点的求解需要将左镜面上的点逐点计算并相加,如此循环迭代下去,最终达到模式稳态分布.

(2)二维矩形腔

图1所示为二维矩形腔的平面示意图,主要结构由两个平面反射镜对称放置构成,图1(a)、(b)分别为立体图和剖面图.

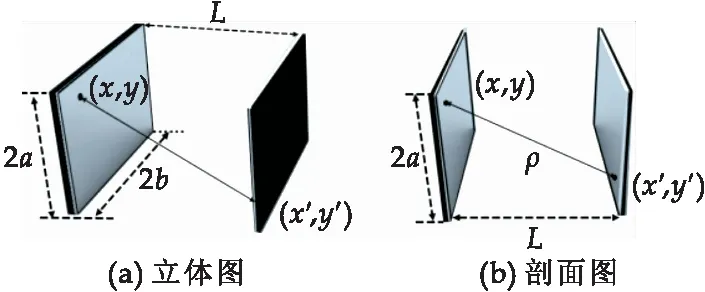
图1 平行平面腔结构图[13]

在矩形腔中,(x′,y′)与(x,y)连线的长度ρ可以表示为：

(2)

其求解方法通过采用分离变量法,按照x、y两个方向把二维菲涅尔-基尔霍夫衍射积分分离为式(3)：

μ(x,y)=μ(x)μ(y)

(3)

其中的μ(x)、μ(y)计算与一维条形腔相同.选取初始场μ1(x),计算μ2(x),并将其进行归一化,依次计算μ3(x)…直到达到模场稳态分布.

1.2 方形镜共焦腔

方形镜共焦腔的平面示意图如图2所示,主要结构由两个方形凹面反射镜M1、M2对称放置构成.图2(a)、(b)分别为正视图和左视图.

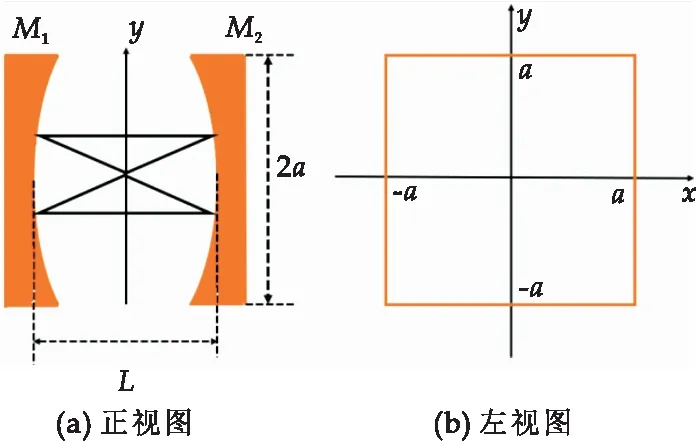
图2 方形镜共焦腔结构图[14] .

其中镜长L、腔长2a与光波长λ之间需要满足关系：

L≫a≫λ

(4)

且

(5)

方形镜共焦反射镜面中心附近,其自再现模的解可近似表示为厄米特多项式和高斯分布函数的乘积,即厄米——高斯(Hermitian-Gaussian)分布.厄米多项式的一般解表示为式(6)：

(6)

其中,[m/2]表示m/2的整数部分.Hermitian-Gaussian分布如式(7)：

(7)

(8)

1.3 圆形镜共焦腔

圆形镜共焦腔的平面示意图如图3所示,主要由两个圆形凹面反射镜对称放置构成.图3(a)、(b)分别为主视图和左视图.

图3 圆形镜谐振腔结构图[15]

圆形镜共焦腔光场模式的积分方程只讨论菲涅耳数足够大时的拉盖尔-高斯近似解.拉盖尔高斯光束是在腔的孔径足够大,即对于激光光束而言,圆形镜的直径无限大的情况下得到的近似光束.其解析表达式的一个特解可表示为:

(9)

然而,这只是旁轴方程的一个特解,还有很多其他形式的特解,同样满足旁轴方程.形如：

(10)

(11)

式(11)中：Lp(ρ)为拉盖尔多项式[16].

基于以上菲涅尔-基尔霍夫积分公式和拉盖尔光束讨论,可以得到当谐振腔菲涅尔数N→∞,圆形镜共焦腔的自在现模分布函数由下述拉盖尔-高斯函数所描述[17]：

(12)

式(12)中：(r,φ)为镜面上的极坐标；Cmn表示归一化常数；与Vmn(r,φ)相应的本征值为:

(13)

2 计算结果与分析

由于光场模式受谐振腔结构的影响而发生变化,需要采用不同的数值分析方式对不同腔型进行模拟.Fox-Li数值迭代法[18]具有普适性,尤其是在计算低阶模时效果更佳.因此,对上文提到的三种腔型的模式分析,可利用Fox-Li数值分析法进行求解.借助Matlab强大的数据处理[19]和图像分析功能,研究在波长632.8 nm的氦氖激光器中,不同菲涅尔数下的振幅相位分布图像,自再现模仿真平面以及三维模场图像和模场花样图,最后针对不同迭代次数下的结果进行分析比较.

2.1 平行平面腔仿真结果及分析

(1)一维条形腔在不同菲涅尔数下模式的振幅和相位分布

图4给出了一维条形腔在菲涅尔数F分别取6.25、2.5和0.5时的振幅相位分布.由图4可以看出,随着一维条形腔菲涅尔数的逐渐减小,场分布曲线由起伏不定趋向于平滑,迭代次数N越小,模式越容易达到稳态分布.同时,菲涅尔数减小到0.5时,振幅分布曲线呈高斯分布,相位分布曲线与球面波的分布形状一致.

(2)二维矩形腔在不同菲涅尔数下模式的振幅和相位分布

图5给出了二维矩形腔在菲涅尔数分别取6.25、2.5和0.5时模式的振幅和相位分布.由图5可以看出,二维矩形腔的模式特点主要是模场分布在整个镜面上,说明矩形腔的衍射损耗较大；在腔镜中心附近,矩形腔的稳态分布特性接近于平面波；其相位分布呈球面状.随着菲涅尔数的减小,矩形腔的振幅和相位分布均趋于平滑,迭代次数N越小,越容易达到稳态分布.

图4 一维条形腔在不同菲涅尔数F和 迭代次数N下模式的振幅和相位分布

图5 二维矩形腔在不同菲涅尔数F和 迭代次数N下模式的振幅相位分布

2.2 方形镜共焦腔仿真结果及分析

对于方形镜共焦腔在菲涅尔数分别选取6.25、2.5和0.5时的振幅一维分布、三维分布和模式光斑分布进行了系统模拟.

(1)方形镜共焦腔在菲涅尔数F=6.25时的振幅分布

方形镜共焦腔在菲涅尔数取6.25时的振幅分布和光斑分布如图6所示.其中，图6(a)、(b)分别为方形镜共焦腔模式的振幅一维和三维分布图.观察四种模式可以看出：当m=n=0时，截面为高斯分布,三维仿真图为空间点扩散函数；当m=0，n=1时,截面为对称的2个高斯分布,有一个零节点在y轴方向,三维仿真图为两个空间点的扩散函数；当m=1,n=0时,有一个零节点在x轴方向,三维仿真图的扩散函数同上；当m=n=1时,截面为对称的4个高斯分布,有2个零值节点,三维仿真图为4个空间点扩散函数；图6(c)为方形镜共焦腔模式的光斑图,从图6(c)可以看出,在F=6.25时,方形镜共焦腔的基模较为集中,无零节点,在r=0处振幅最大,光斑体积较小；随着m、n的增大,零节点增多,光斑呈现多模形式.

图6 方形镜共焦腔在菲涅尔数F=6.25时的仿真

(2)方形镜共焦腔在菲涅耳数F=2.5时的振幅分布

方形镜共焦腔在菲涅尔数取2.5时的振幅分布和光斑分布如图7所示.其中，图7(a)、(b)分别为方形镜共焦腔模式振幅的三维分布和一维截面分布,图7(c)为方形镜共焦腔模式的光斑图.从图7可以看出：总体模式特征与菲涅尔数取6.25时无差别.但是,从图7(c)可以看出,随着菲涅耳数的减小,光斑面积较之前变大,这是由于谐振腔菲涅耳数变小时,高阶模的损耗相应增加的缘故.

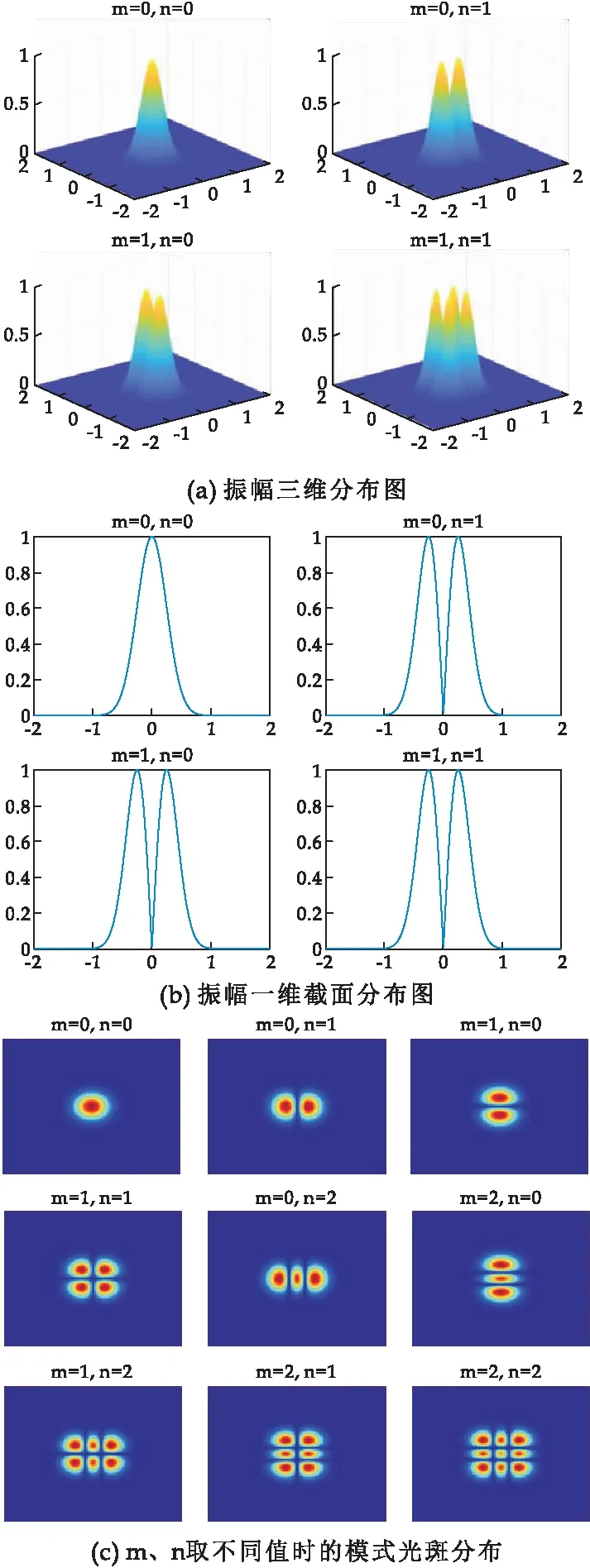
图7 方形镜共焦腔在菲涅尔数F=2.5时的仿真

(3) 方形镜共焦腔在菲涅尔数F=0.5时的振幅分布

方形镜共焦腔在菲涅尔数取0.5时的振幅分布和光斑分布如图8所示.其中,图8(a)、(b)分别为方形镜共焦腔模式振幅的三维分布图和一维截面图,图8(c)为方形镜共焦腔的模式光斑图.从图8可以看出：总体模式特征与前两种情况趋于一致,图8(c)光斑图同样显示随着菲涅耳数的进一步减小,光斑面积呈现明显变大趋势,且F=0.5时模式特征与基模截面呈现高斯分布.

图8 方形镜共焦腔在菲涅尔数F=0.5时的仿真

总之,方形镜共焦腔的基模截面为高斯分布,三维仿真图为空间点扩散函数,在r=0处振幅最大,无节线；高阶模与基模相比,随着m、n值的增大,零节点值越多,空间点扩散函数的个数越多,模体积越大.不同菲涅尔数下的模式光斑图表明：菲涅尔数越小,模式光斑体积越大,表示从激活介质中提取的能量越多,发生模式振荡时参与的粒子数越多,获得优质光束输出的可能性越大.因此,适当减小菲涅尔数,方形镜共焦腔能够获得优质的光束输出,在满足理论条件的基础上适当选择高阶模组,则能够获得满足高功率器件需求的激光模式输出.

2.3 圆形镜共焦腔仿真结果分析[20]

圆形镜共焦腔亦在菲涅尔数分别选取6.25、2.5和0.5时，对其振幅分布进行了模拟.

(1)圆形镜共焦腔在菲涅耳数F=6.25时的振幅分布

圆形镜共焦腔在菲涅尔数取6.25时的振幅分布和模式光斑分布如图9所示.其中,图9(a)、(b)分别为圆形镜共焦腔模式振幅的三维分布图和一维截面图,图9(c)为m、n取不同值时,模式的光斑分布.从图9可以看出：当m=n=0时，模式三维分布和一维截面分布均为高斯分布,三维仿真图为空间点扩散(脉冲响应)函数.当m=0，n=1时,与方形镜共焦腔类似,截面为轴向对称的2个高斯分布,三维仿真图为2个空间点扩散函数,有一个零值节点.当m=1、n=0时,截面为径向Sa(抽样)函数分布,其特点是在中心处取得最大值,随着自变量绝对值的增大呈振荡减小趋势,最终趋近于0,三维图像近似为衍射光斑分布,有一个零值节点.当m=n=1时,截面为轴对称的两个Sa函数分布,三维仿真图近似为两个衍射光斑分布,有两个零值节点.图9(c)的模式光斑图可以看出,圆形镜共焦腔的基模截面为高斯分布,高阶模截面随着m、n的增加呈现径向衍射光斑与轴向光斑分裂交织分布,且其衍射损耗比方形镜共焦腔更大一点.

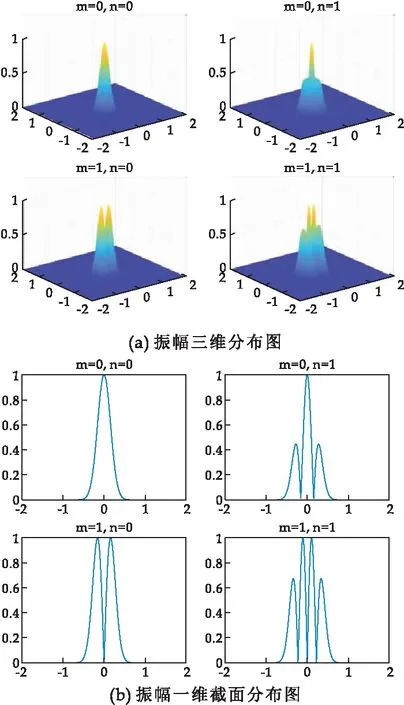
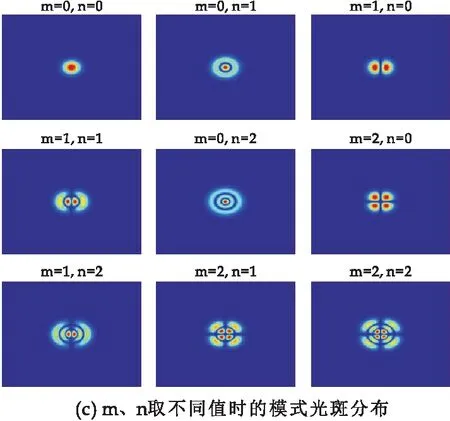
图9 圆形镜共焦腔在菲涅耳数F=6.25时的仿真

(2)圆形镜共焦腔在菲涅尔数F=2.5时的模式分布

圆形镜共焦腔在菲涅尔数取2.5时的振幅分布和光斑分布如图10所示.由图10可以看出：当菲涅耳数F减小为2.5时,其模式特征与F=6.25时无差别,但其光斑图10(c)显示光斑面积较之前变大,这同样与谐振腔菲涅耳数变小时,高阶模的损耗相应增加相关.

(3)圆形镜共焦腔在菲涅尔数F=0.5时的模式分布

圆形镜共焦腔在菲涅尔数取0.5时的振幅分布和模式光斑分布如图11所示.从图11可以看出,F=0.5时模式特征与前两种情况下基本趋于一致,基模截面呈现高斯分布状,三维仿真图为空间点扩散函数,高阶模截面图近似为Sa函数分布,三维仿真图近似为衍射光斑,光斑面积随着菲涅尔数的减小而增大.

总之,圆形镜共焦腔的基模截面呈现高斯分布状,三维仿真图为空间点扩散函数,高阶模截面图近似为Sa函数分布,三维仿真图近似为衍射光斑分布,衍射损耗介于平行平面腔和方形镜共焦腔之间.圆形镜共焦腔模式随菲涅尔数的变化与方形镜趋于一致,菲涅尔数越小,模式光斑面积越大,高阶模的抑制能力越强.

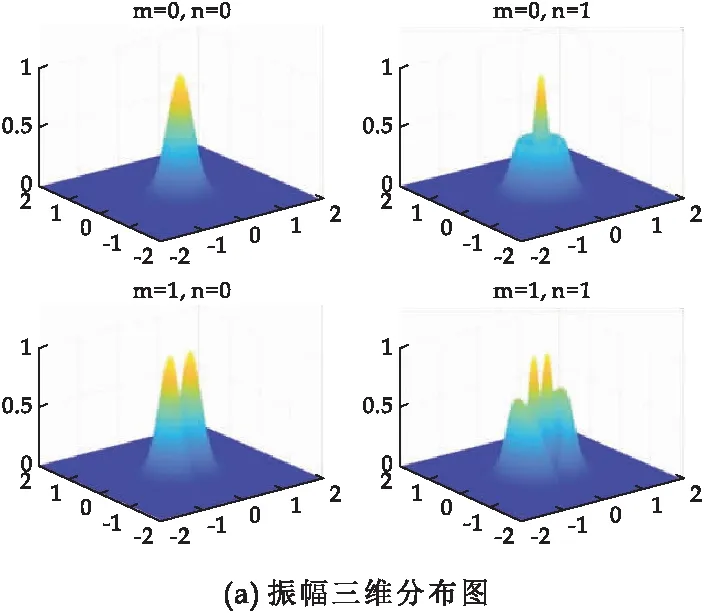
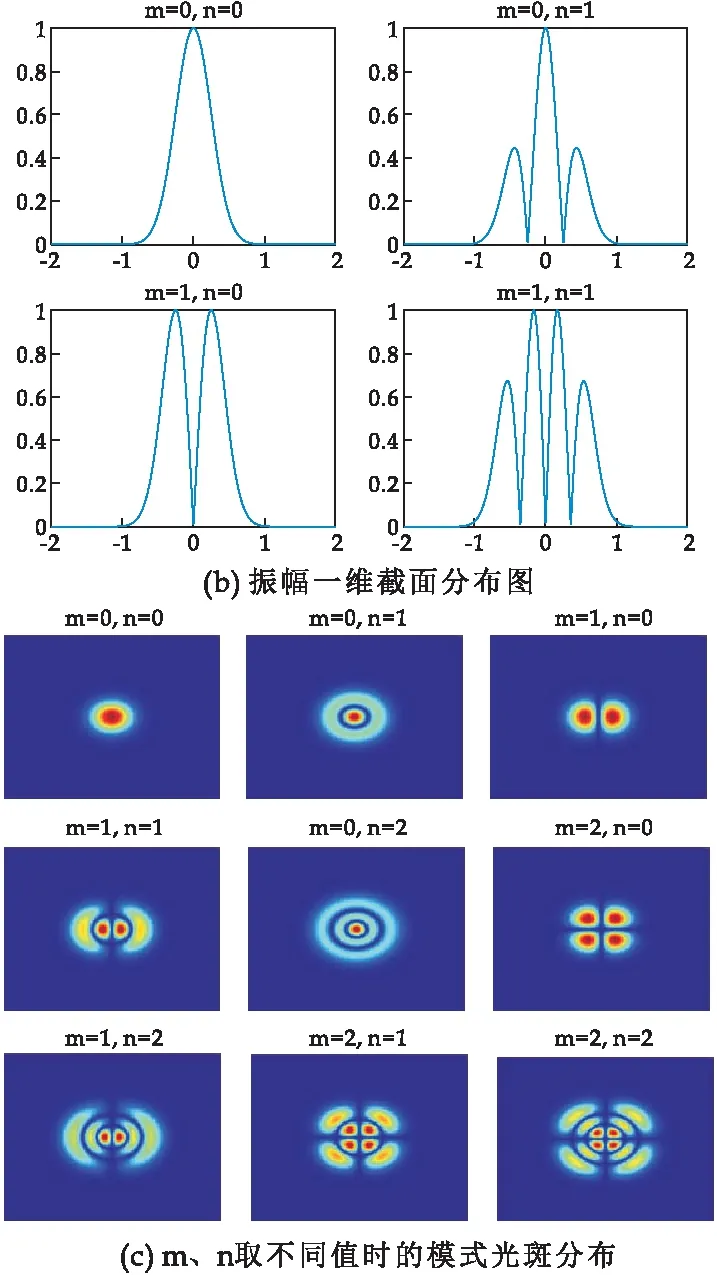
图10 圆形镜共焦腔在菲涅尔数F=2.5时的仿真

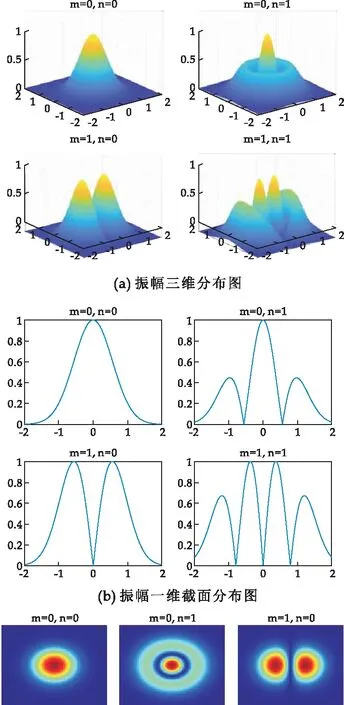
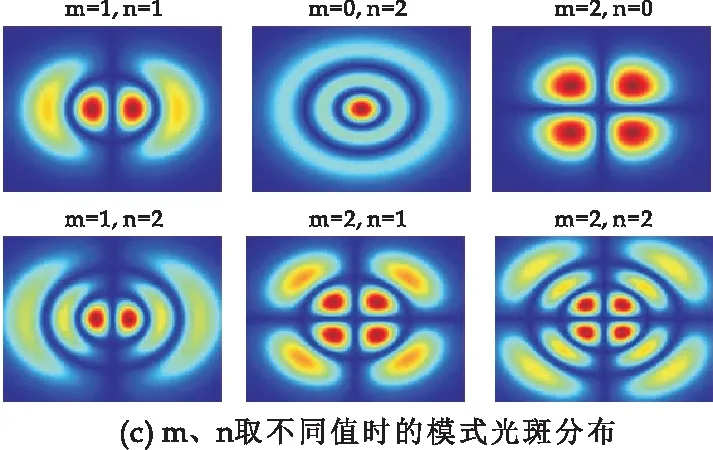
图11 圆形镜共焦腔在菲涅耳数F=0.5时的仿真

3 结论

平行平面腔的模式特征在小菲涅尔数的情况下振幅分布为高斯分布,相位图像呈现球面波状,模式体积大、分散在整个镜面上,说明其衍射损耗和几何损耗较大,因此不适用于小增益情况下的激光输出[21].方形镜共焦腔的模式集中在镜面中心附近,基模截面为高斯分布,三维仿真图为空间点扩散函数,在中心原点处振幅最大,无节线；高阶模与基模相比,模的阶数越大,零值节点越多,空间点扩散函数的个数越多,模体积越大.在高功率选模时纯粹的基模无法满足功率需求,可以从高阶模中选择更为合适的模组,其优点在于单程损耗较小,基模更为集中,可应用于精细度要求较高的激光器.圆形镜共焦腔基模截面呈现高斯分布状,三维仿真图为空间点扩散函数,高阶模截面图近似为Sa(取样函数)分布,三维仿真图近似为环形衍射光斑,单程损耗介于平行平面腔和方形镜共焦腔之间.该研究为激光器谐振腔结构的优化设计及激光器光束输出质量的提升具有重要的指导意义.