基于MA-BiLSTM的多时间窗航班过站时间估计方法

曹卫东, 梁 陈

(中国民航大学 计算机科学与技术学院, 天津 300300)

0 引言

航空公司为提高飞机使用率，通常采用由单架飞机一天内连续执行多个航班任务的航班链运行方式，某架飞机若在执行航班链的过程中未出现延误情况，各过站机场的实际过站时间与计划过站时间相差不大；但是当航班链中发生了前航延误，后续航班若再受到过站机场运行效率较低或恶劣天气等因素的影响，较大可能出现延误波及，产生更多的航班延误[1].因此，精准估计航班过站时间可以帮助航空公司适时调整航班计划，为机场进行资源调配提供决策依据，降低航空公司由航班链运行的脆弱性导致的成本损失[2]，同时帮助旅客及时调整出行计划，降低旅客时间和经济损失.

针对航班延误吸收与波及问题，众多学者从不同角度进行研究.Chen等[3]通过随机森林、LightGBM和XGBoost三种模型分别预测的结果进行二次训练，提出了一种多模型融合的航班延误预测模型；朱星辉等[4]依据基于航班延误等级，调整过站时间，提高航班计划的鲁棒性；高强等[5]利用波及延误树构建以初始航班延误为根节点触发的延误传播过程，对航班过站松弛时间重分配，降低延误时间.丁建立等[6]利用贝叶斯网络增量学习的特性，依赖贝叶斯估计动态修正贝叶斯网络参数，动态更新过站时间估计值；邢志伟等[7]针对单机场服务保障流程数据采用贝叶斯网络架构，再结合条件概率推理方法动态估计了航班预计离港时间.何坚等[8]基于多机场真实运营数据，构建了基于LightGBM的航班中转时间预测模型.以上学者研究方法多采用有监督的机器学习方法，预测效果受影响因素个数限制，为降低模型复杂度，提高模型准确度，需先对航班、天气等数据进行特征提取，而深度学习模型可以增加输入数据维度，自动提取特征并较好地挖掘其中的潜在关系.

此外，航班链各机场过站数据随航班计划执行航班状态不断更新，具有时序特性，数据更新时间间隔随航班计划安排长短不一.LIM等[9]经过实验探索发现，基于深度学习的时间序列预测效果较优.注意力机制[10]模仿人类大脑的注意力思维方式，可通过网络自主学习出的一组权重系数，并以概率动态加权的方式来强调关注目标和抑制无效信息.Du等[11]采用一种融合注意力机制和双向长短时记忆网络(Bi-LSTM)进行时序数据预测方法，在预测精度和算法鲁棒性方面取得较好的效果.综上可以得到采用Bi-LSTM模型[12]在解决非固定时间步长时序任务时，具有充分探索全局上下文信息的能力，注意力机制[13]可以高效提取关注目标主要特征信息.基于此，结合航班链过站数据的时序特征、数据量大、影响因素多等特性，提出了一种基于MA-BiLSTM (Mixed Attention based Bidirectional Long Short-Term Memory)的多时间窗航班过站时间估计方法.采用具有可以获得双向信息的Bi-LSTM模型进行基础建模，为更加高效选择聚焦属性，在Bi-LSTM网络模型的基础上增加时间和多维属性的混合注意力机制，最后根据航班链执行状态设置不同长度的时间窗，采用多时间窗滑动推进的方法对各机场过站时间进行动态估计.

1 航班链航班过站流程

单架飞机一天内通常会连续到达多个过站机场，执行多段航班，称为航班链[14].如图1所示，长度为7的航班链.

图1 长度为7的航班链

在航班链中，飞机到达过站机场后，完成一系列航班过站保障流程和旅客登机程序等.如图2所示，实际过站时间等于实际离港时间和前序实际到港时间之差.

图2 航班过站流程

2 航班过站多维度影响因素分析

多数研究受限于数据难以收集，同时传统机器学习方法对影响因素选择个数有较高要求，既往研究选用的影响因素较少[6].本文在现有数据的基础上，结合专家经验，从天气因素、机场因素、飞机因素及航班相关时间信息四个方面选择影响因素.

2.1 天气因素

根据机场天气状况可以判断是否进行航班起降，主要包括能见度等参考指标.其中天气描述参考指标综合概括机场的天气状况，本文将其划分为5个等级，如表1所示.

2.2 机场因素

用于量化机场规模和机场运行效率，主要包括机场类型等.其中标准机场地面滑行时间是民航局为客观反映不同机场实际地面运行效率而设定的，如表2所示，将国内机场分为4类，并给出对应的标准机场地面滑行时间.

此外，过站机场小时吞吐量是指过站机场每小时到港航班架次和离港航班架次总和，为更准确地描述机场实时运营效率，增加过站机场小时吞吐量为过站时间影响因素；机场停机位的远近会影响实际到港时间，增加是否为远机位作为影响因素.

表1 天气描述等级

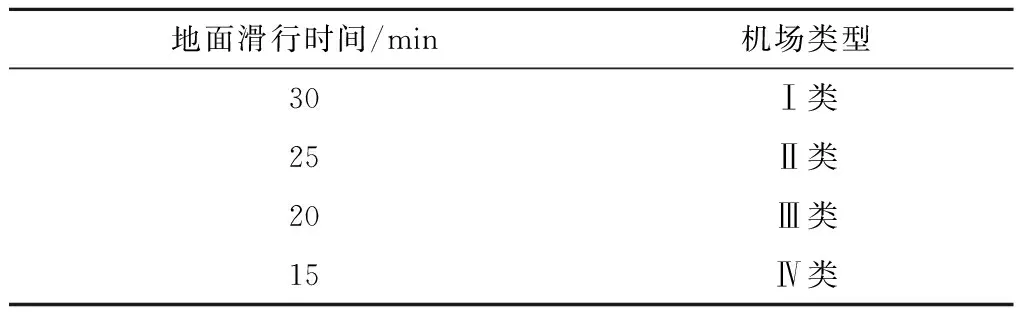
表2 全国机场等级

2.3 飞机因素

用于量化航空公司对航班计划制定合理性以及应急保障能力.其中，航空公司、机龄和座位数等飞机属性不同，航班过站时间也会不同.当航空公司和过站机场相同，机型越大，座位数越多，则过站时间越长.以某大型航空公司为例，根据不同机型的座位数、过站机场，统计最小过站时间如表3所示.

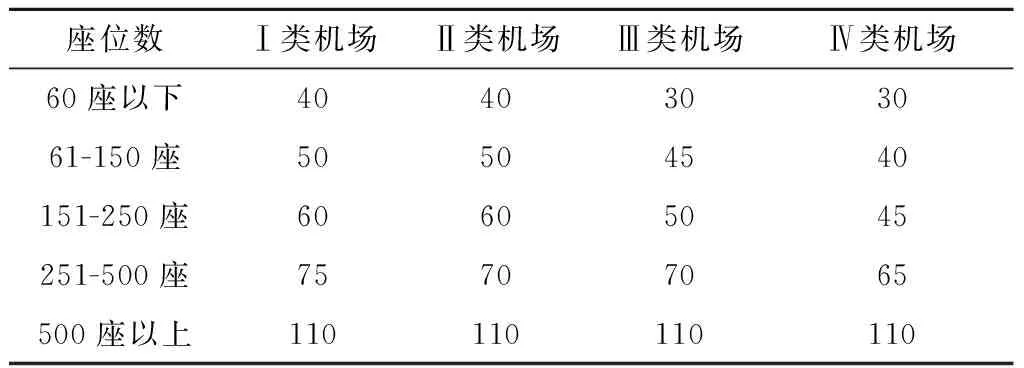
表3 某大型航空公司最小过站时间(分钟)

2.4 航班相关时间信息

用于量化航班链相关时间信息，航班过站关键时间节点如图2所示.首先，为探究各航段计划飞行时间松弛度对航班延误时间的影响，增加了计划飞行时间和实际飞行时间作为影响因素.其次，为凸显出季节、节假日和工作日对机场进离港流量的影响，增加了相应字段作为影响因素.同时，为进一步探究繁忙时段对航班链过站延误波及的影响，增加了繁忙时段作为影响因素.

综上，航班链航班的机场过站时间影响因素如图3所示，其中灰色部分表示前序航班相关信息.

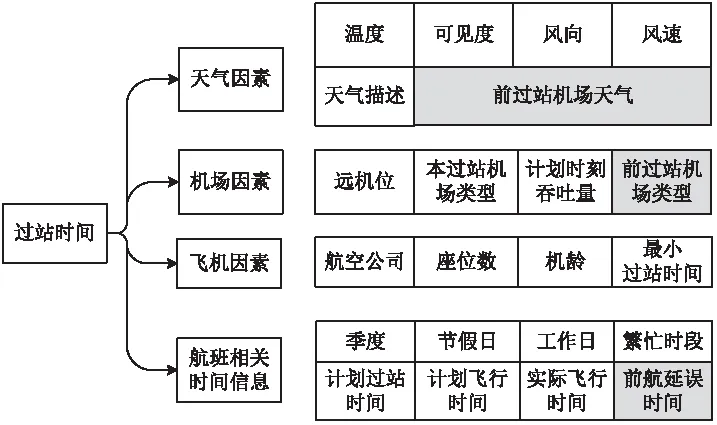
图3 过站时间影响因素

3 过站时间预测模型

构建基于MA-BiLSTM网络的航班过站时间动态估计模型，以航班上、下游过站机场天气因素、机场因素、飞机因素及航班相关时间因素作为模型输入；再根据航班链执行状态设置不同长度的时间窗，采用MA-BiLSTM模型预测出下游不同过站机场的预计过站时间；最后采用加权平均方法融合多时间窗估计结果，提高预测精度.

3.1 MA-BiLSTM模型

MA-BiLSTM模型由Bi-LSTM网络层、Mixed Attention层和Dense层组成，结构如图4所示.模型是基于Bi-LSTM网络对航班过站数据进行建模，得到上游和下游机场过站数据序列之间的关系，再增加感知时间(Time)和多维属性(Factor)的混合注意力机制(Mixed Attention)，获取上下游不同过站机场不同因素的影响重要程度，最终全连接层(Dense)输出下游不同过站机场的预计过站时间.

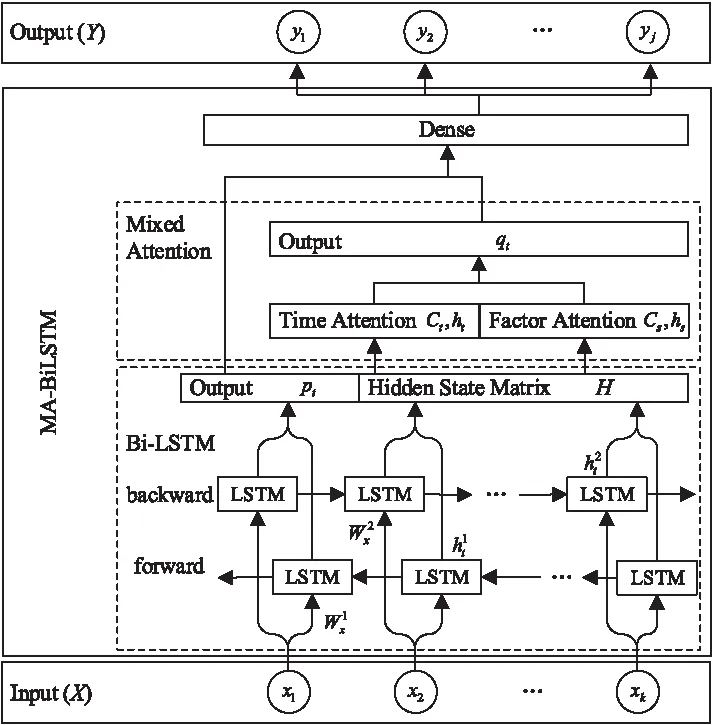
图4 MA-BiLSTM模型

Bi-LSTM[13]网络层利用Bi-LSTM网络可获得双向时序信息的特性，得到上游和下游机场间的时序记忆信息.Bi-LSTM是在LSTM[15]上扩展，结合BRNN[16]原理，在输入序列上分别地向前和向后训练两个LSTM，其输出由这两个LSTM共同决定，从而可以充分学习某时刻过去和未来的时序信息[17].LSTM是在RNN[18]基础上改进，其特有的记忆和遗忘方式，能够解决许多使用固定长度的时间窗无法解决的时间序列任务.

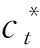
遗忘门：

ft=σ(Wf[ht-1,xt]+bf)

(1)

输入门：

it=σ(Wi[ht-1,xt]+bi)

(2)

(3)

(4)

输出门：

yt=σ(Wy[ht-1,xt]+by)

(5)

ht=yt*tanh(ct)

(6)

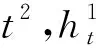
(7)

(8)

(9)

设H表示对过站数据输入时间序列进行Bi-LSTM网络构建后得到的隐状态矩阵，其中行向量代表同一变量的所有时间步构成的向量集合，列向量代表同一时间步下的所有变量构成的向量集合，H1和H2分别表示向前和向后两个方向得到的隐状态矩阵.具体描述如下：

(10)

Mixed Attention层分别针对时间和多维属性进行注意力训练，得到了混合注意力权重矩阵.具体计算如下：

(11)

(12)

(13)

(14)

qt=τ(Wc[Ct;ht;Cs;hs])+bq

(15)

式(11)～(15)中：αt表示当前输入的时间步为t时隐藏层的注意力权重，Ct表示各时间步加权平均后的权重；βs表示影响因素s对应的注意力权重，Cs表示各因素加权平均后的权重；qt表示混合注意力机制结果输出.

Dense层通过线性运算得出下游各过站机场的预计过站时间.主要进行MA-BiLSTM网络层和输出层之间的过渡，最终输出预计过站时间向量y.

3.2 模型输入及输出

本文预测场景为：假设某飞机的航班计划为一天连续飞行N趟航班，已知首航起飞已完成，后续经过N-1个过站机场，完成前i-1趟航班，到达第i个过站机场，依据第i-k个至第i-1个过站数据，预测此飞机在第i个至第i+j-1个过站机场的过站时间.其中，k表示上游过站机场个数，j表示预测下游过站机场个数.

定义I为模型输入的航班链过站数据集合，表示如下:

(16)

式(16)中：n表示输入过站数据总条数，Xi表示第i条输入过站数据，xi,t表示第i条数据的第t个过站数据序列，分为离散型数据变量和连续型数据变量.离散型数据变量主要包括机场类型、航空公司等变量，由原始数据进行One-Hot编码[19]处理得到.连续型数据变量主要包括温度、过站机场小时吞吐量和飞行时间等变量，使用Min-Max标准化法[11]对原始数据进行归一化得到.

定义O为模型输出的过站数据集合，表示如下:

(17)

式(17)中：n表示输出预计过站时间总条数，Yi表示第i条输出预计过站时间向量，yi,t为第i条数据预计第t个过站机场的过站时间，由模型输出结果进行归一化还原后得到.

3.3 多时间窗过站时间估计

随着航班链运行状态的变化，为及时降低因前航延误带来的延误波及，采用多时间窗滑动的方式进行过站时间估计，图5为多时间窗航班过站时间估计流程图.

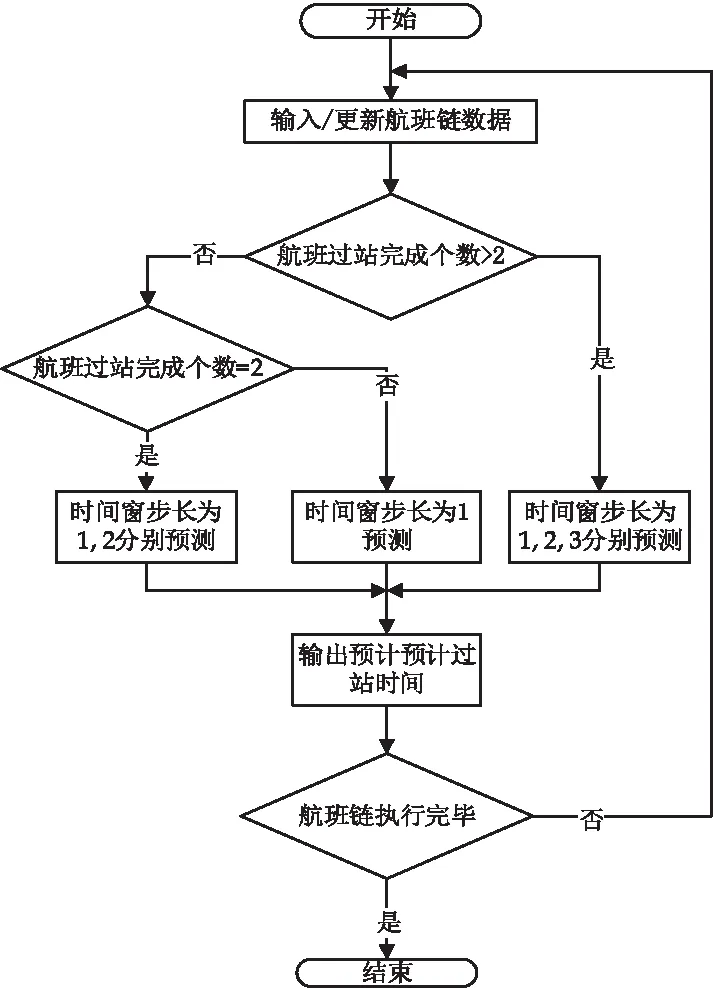
图5 多时间窗过站时间估计流程

具体流程如下所示：

步骤1输入或更新航班链数据.

步骤2判断航班链最新过站完成状态，当过站个数大于2时，分别采用时间窗长度为1,2,3模型进行预测，跳转至第5步；否则跳转至第3步.

步骤3当过站个数为2时，分别采用输入时间窗长度为1,2模型进行预测，跳转至第5步；否则跳转至第4步.

步骤4当过站个数为1时，采用输入时间窗长度为1模型进行预测，跳转至第5步.

步骤5对多时间窗预测结果进行融合，跳转至第6步.

步骤6判断航班链是否执行完毕，如果否，等待更新航班链状态，跳转至步骤1；否则流程结束.

4 实验结果及分析

4.1 实验数据

实验原始数据为全国2019年一整年的真实航班数据，覆盖全国136个机场，数据量约350万条.一条航班数据主要包含航班过站关键时间节点(见图2)等字段，不包含前序航班相关数据.需要先对航班数据进行预处理转化为航班链过站数据，使用JetBrains PyCharm进行编程实现，运行内存为16G.

4.1.1 航班数据清洗

某飞机一天内先后到达A、B、…等多个机场，若航空公司售卖联程机票，航班数据中可能同时包含A-B、B-C、…等单航段及A-(B)-C、B-(C)-D、…等多航段数据，或者包含部分单航段和部分多航段数据，对重复航段的数据进行重组，保留最小的单航段数据.

4.1.2 航班链过站数据集成

将得到的航班数据通过飞机注册号这一唯一标识来匹配同一架飞机执行的航班；通过机场唯一标识匹配天气相关属性数据；通过飞机机型匹配飞机相关属性数据；通过日期拼接成航班链过站数据.

4.1.3 航班链数据选择

对航班链中每条过站数据的过站时间进行过站时间等级统计.根据时间长度分为5个等级，如表4所示.

表4 时间长度等级

分析不同过站时间等级航班数占总过站架次百分比，其中计划过站时间在Level 1范围内占比33%，但实际过站时间在Level 1范围内占比9%，大约24%航班过站时间高于计划过站时间；计划过站时间长度和实际过站时间长度在Level 5范围内占比稳定，说明当过站时间大于4 h时，过站时间安排较为充裕，较大可能将前序航班延误吸收，因此设定当过站时间大于4 h，表示航班链执行末班航班.对数据集中航班链过站延误时间进行统计，航班链执行过程中发生过站延误时间的航班占比约为20%，发生首航延误的航班占比约为14%.

为探究航班链不同执行状态下，机场过站时间对后续航班延误的影响，对航班链中占较大比重的未发生延误数据进行随机采样处理，使延误与未延误数据保持平衡，提高训练模型的鲁棒性.

4.2 结果与分析

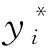
(18)

(19)

4.2.1 多模型对比分析

通常单架飞机单日过站机场个数约为2至6个，即航班链长度为3至7，航班链长度为5占比总航班链个数的40%.选择航班链长度为5的航班链数据进行MA-BiLSTM模型的准确度评估，选用RNN[18]、LSTM[18]、Bi-LSTM[17]和Bi-LSTM+Att[11]四种作为对比模型.各模型基于Tensorflow框架进行网络构建和训练，对每个模型多次训练调优，得到各模型超参数(学习率、训练轮次、随机失活比例)；依赖sklearn编程库，对数据集按照8∶2的比例多次划分训练集和测试集.

同时，为探索输入前序过站机场个数和输出预测后续过站机场个数对预测模型预测本机场过站时间的影响，各模型设置不同长度时间窗的输入和输出进行实验，表5和表6为其5次MAE和RMSE评价结果的平均值，其中，时间窗长(k,j)表示输入过站数据的前序过站机场个数为k和输出预计过站时间的机场个数为j.

多个模型结果对比分析发现，当选择相同的时间步时，MA-BiLSTM模型的MAE值和RMSE值均小于四种对比模型，MA-BiLSTM模型在预测航班过站时间方面有较好的准确性.其中，当时间窗长为(2,1)时，MA-BiLSTM模型评估效果最好，MAE值和RMSE值分别为2.45 min和3.95 min，较Bi-LSTM+Att模型MAE值提升1.1 min，RMSE值提升1.92 min，即输入已完成2个机场的过站数据，能够更为准确预测后续1个机场的过站时间.

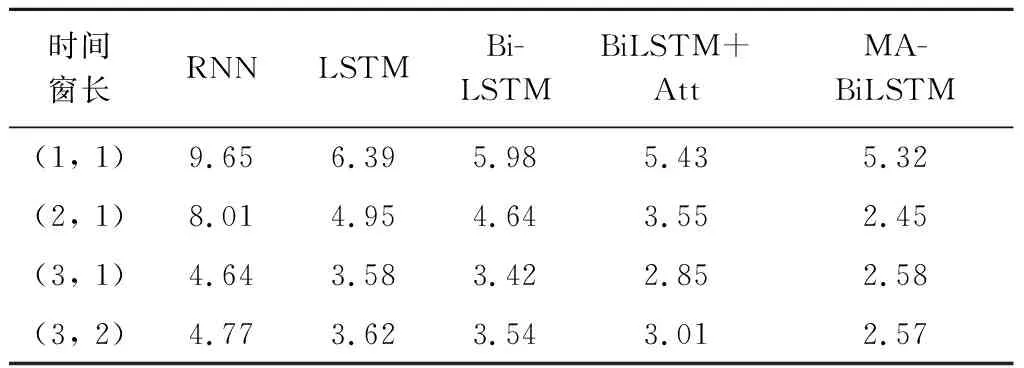
表5 长度为5的航班链各模型MAE结果

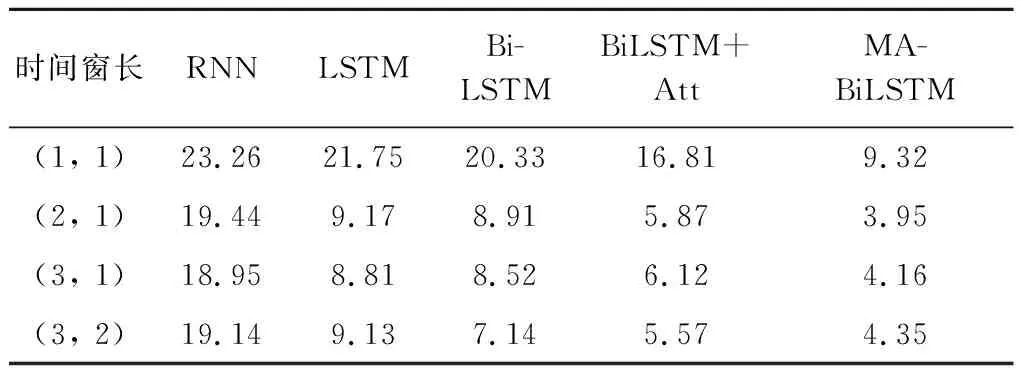
表6 长度为5的航班链各模型RMSE结果

4.2.2 模型准确度验证

为进一步验证MA-BiLSTM模型的准确性，选择时间窗长(3,1)时，分别按照月份和工作日对结果进行MAE和RMSE值验证，图6为各月份的评估结果，图7为各季度工作日与节假日的评预测估结果.

依据民航航班计划安排将12个月分为夏秋季和冬春季，夏秋季是指4月至10月，其余月份为冬春季，其中夏秋季平均航班延误率高于冬春季，且6月份至8月份的延误率最高.如图6所示，全年12月份验证结果均匀分布在全年的综合评估结果上下，其中，6月份至8月份评估结果高于全年的综合评估结果受台风、暴雨等天气影响因素较大.

对比全年节假日和工作日平均延误率发现，节假日平均每日运输量高于工作日，但节假日延误率低于工作日延误率.如图7所示，整体评估结果分布均匀，说明MA-BiLSTM模型预测效果良好.其中各季度节假日优于工作日评估指标受节假日调整运营保障计划的影响.

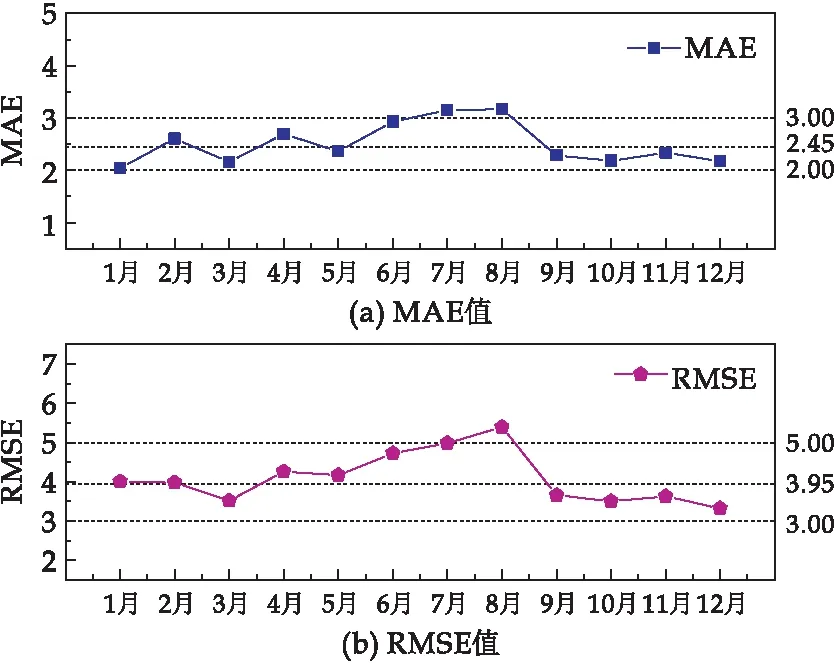
图6 月份评估结果

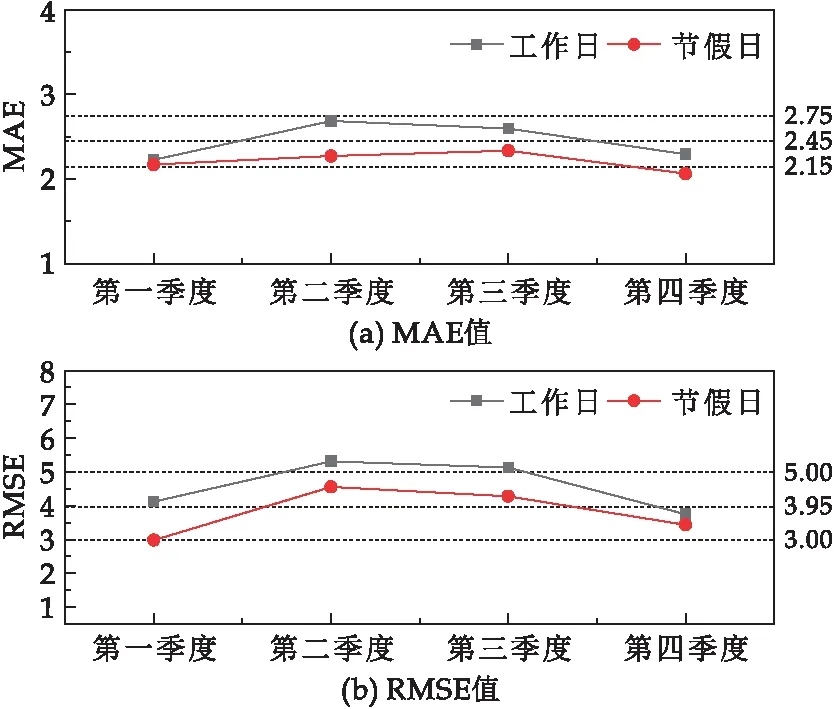
图7 工作日与节假日评估结果

4.2.3 多航班链实验分析

为验证航班过站时间动态估计精度，选择数据集中航班链长度为4、5、6和7根据图5流程进行多时间窗滑动方法估计航班过站时间.首先采用多次训练调优得到不同长度时间窗预测模型作为基础模型，随着多时间窗的推进增加模型训练数据，由于新增数据量较历史数据较小，调整模型训练超参数，动态更新模型参数，表7和表8为MA-BiLSTM模型预测结果，表中“-”表示不存在数据结果，表中“A、B、…”表示航班链第1个、第2个、…过站机场.

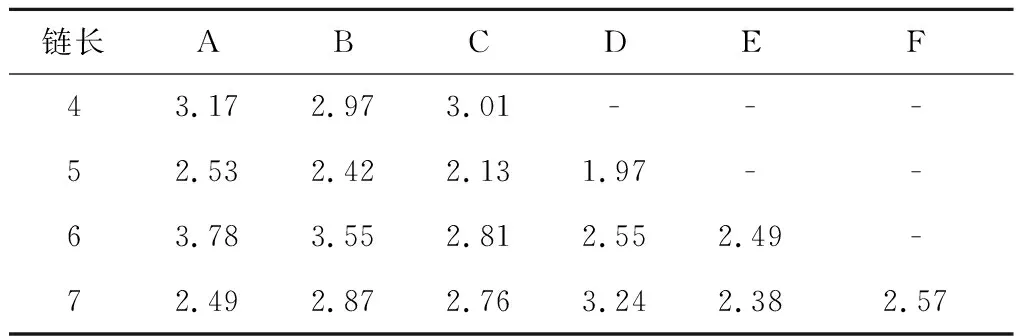
表7 MA-BiLSTM模型MAE结果

表8 MA-BiLSTM模型RMSE结果

通过对比不同航班链长度评价指标发现，当航班链长度为4时，3个过站机场预测结果随时间窗推动波动不大，说明预测效果较为稳定；当航班链为7时，6个过站机场预测结果随多时间窗滑动推进在一定范围内波动相对较大.当航班链为5时，MA-BiLSTM模型预测结果比单时间窗预测结果MAE值和RMSE值均有显著提升，说明基于MA-BiLSTM的多时间窗航班过站时间估计方法有良好效果.

5 结论

本文充分提取航班过站时间的影响因素，从天气因素、机场因素、飞机因素和航班相关时间信息四个方面进行影响因素选择，基于可充分学习前后段时序特征的Bi-LSTM网络，融合时间和多属性两维度的混合注意力机制，提出了基于MA-BiLSTM的多时间窗航班过站时间估计方法.首先，与常用模型对比实验，进一步探究了输入和输出过站机场个数对多模型预测模型的影响，采用不同模型和不同时间步长进行训练预测，得出了MA-BiLSTM模型预测效果最好.最后采用了多时间窗滑动推进的方式，分别对不同长度的航班链进行航班过站时间动态估计，验证了MA-BiLSTM的多时间窗航班过站时间估计方法有较好的预测准确性.在今后的研究中，如果能够加入机场保障数据，将进一步提高航班过站时间预测模型性能.