刚性吊杆拱桥主要受力构件冲击效应差异性

雷家艳，崔怡观，周志成，王子豪

(1.厦门大学建筑与土木工程学院，福建 厦门 361005;2.中铁一局集团有限公司广州分公司，广东 广州 511400)

我国南京大胜关长江大桥、宜宾金沙江公铁两用特大桥均采用了刚性吊杆，相对于钢绞线柔性吊杆，刚性吊杆公路拱桥比较少见，因此对刚性吊杆拱桥开展动力性能研究具有重要的意义.冲击系数是重要的结构动力性能指标之一，我国现行的公路桥梁设计规范[1]对冲击系数的规定仅依据结构基频计算，已有研究资料表明，依据规范计算的复杂结构体系桥梁冲击系数明显偏小，且复杂结构体系中各构件的冲击效应差异性明显[2-3].

当前对桥梁冲击效应的数值研究主要采用车桥耦合振动分析方法，针对拱梁组合体系的复杂桥梁，朱劲松等[4]采用二维车桥耦合振动分析方法对中下承式拱桥的柔性吊杆应力冲击系数不均匀性进行了分析.Huang[5]考虑桥梁跨长及矢垮比等因素，通过比较振型叠加法和Newmark算法，分析了桥面、拱肋以及墩柱的动力响应.霍学晋等[6]基于四自由度二轴车辆模型，从行车速度、结构阻尼、路面不平整度、行车方向、轴距等角度对蝶形拱桥拱肋、主梁及吊索的冲击系数进行研究，为该桥型的设计提供参考依据.Wang等[7]基于三维车桥耦合模型，运用四阶Runge- Kutta法分析车桥耦合方程，研究了车辆荷载、车速及路面条件等几个重要参数对钢管混凝土拱桥的主拱、主梁及吊杆的动力冲击系数的影响.Gao等[8]在不同车速和不同路面平整度的影响下，对钢管混凝土拱桥的主梁、主拱肋和吊杆等构件的冲击效应进行了数值研究.

然而已有的研究资料主要针对钢绞线柔性吊杆拱桥，且为了减少车桥耦合迭代计算的工作量，通常采用较为简化的车辆或桥梁模型，在参数分析中也甚少涉及不同车道、不同车辆模型对冲击效应的影响.因此，本文以厦门天圆大桥(单拱肋刚性吊杆拱桥)为工程背景，建立拱桥精细三维模型，利用自编的三维车-桥耦合振动分析程序，分别研究了拱桥箱型主梁、刚性吊杆及拱肋冲击效应的差异性，探讨了汽车车速、路面不平整度、不同车辆模型和车辆横向行驶车道等影响因素对桥梁各主要构件冲击效应的影响，对该类桥梁的动力性能评估、运营及维护提出建议.最后利用桥梁结构动力测试数据，验证了数值计算结果的合理性.

1 三维车桥耦合振动体系的分离迭代求解方法

车-桥系统整体耦合法是将车辆与桥梁的运动方程合并为一个耦合方程，采用Runge- Kutta法、Wilson-θ法、Newmark-β法等积分方法联立求解车辆与桥梁耦合振动方程，计算速度快，但是该方法在求解自由度较多的模型时，相关矩阵维数巨大.分离迭代法是将车辆和桥梁视为两个分离体系，分别求解车辆模型和桥梁模型的动力平衡方程，其中车辆振动方程如式(1)所示，通过车辆与桥梁接触点的位移协调条件加以耦合，分别进行迭代，桥梁振动计算可以在通用有限元程序中实现，车辆的振动分析迭代过程可利用MATLAB进行编程计算，虽然迭代过程计算量大，计算速度较慢，但分离迭代法思路清晰、实用性强，适合于复杂结构体系桥梁的三维车桥耦合振动分析[9].

(1)

式中：Mv、Cv和Kv分别为车辆的质量矩阵、阻尼矩阵和刚度矩阵，Gv为重力荷载向量，Fv为轮胎和桥面接触点的瞬时耦合荷载向量.

本文将路面不平整度作为一种激励参数整合到迭代法中，利用Newmark-β法对车辆振动方程进行求解，通过位移协调条件和力的平衡条件计算出车桥接触点相互作用力，并施加到桥梁有限元模型中，其表达式分别如式(2)和(3)所示.通过有限元软件计算并提取桥面位移时程，若满足位移耦合条件，则结束迭代过程，反之，重复以上迭代步骤，直到提取出的桥面位移时程满足位移耦合条件.具体求解流程如图1所示.

图1 分离迭代法求解车桥耦合问题流程图Fig.1 Flow of vehicle-bridge coupling analysis with separated iteration method

ui=zi-yi-ri,

(2)

式中：zi为车轮与桥面接触位置车轮的竖向位移，yi为车轮与桥面接触位置桥梁的竖向位移，ri为车轮与桥面接触位置桥面的不平顺度.

(3)

路面不平整度是车桥耦合振动分析中的一个重要激励源，且具有较大的随机性，一般可用功率谱密度函数表示路面不平整度随频率的变化[10].如式(4)所示：

(4)

式中：n为空间频率，单位为(cycle/m)；n0为标准空间频率，n0=0.1，单位为(cycle/m)，为空间频率的低频段与高频段的分界；φ(n0)是标准空间频率对应的路面粗糙系数，单位为m3/cycle，其值决定了路面的平顺程度；ω是频率指数，取为2；n1和n2是路面功率谱在低频段和高频段分别采用不同的指数.

本文后续分析中，根据《车辆振动输入—路面平度表示方法》给定的功率谱密度函数，考虑A、B、C 3种路面不平度等级，在MATLAB软件中编制运算程序进行傅里叶逆变换，得到图2所示的路面不平整度样本.计算中选用美国《国家公路与运输协会标准》(AASHTO)中的HS20-44车型和中国《公路桥涵设计通用规范》(JTG D60—2015)中的五轴车模型(文中记为5axle-CHN车型)，两种车辆模型的参数见参考文献[11-12].为了验证本文车桥耦合振动分析方法的正确性，采用与文献[12]中相同的车桥模型，相同测点的应变动力时程对比如图3所示，本文计算方法因精细三维桥梁模型的单元数量巨大，迭代步长比参考文献[11-12]中的方法长，总迭代步数减少使时程曲线的波峰波谷数量减少，但两种方法计算结果的总体趋势及最大值符合较好.

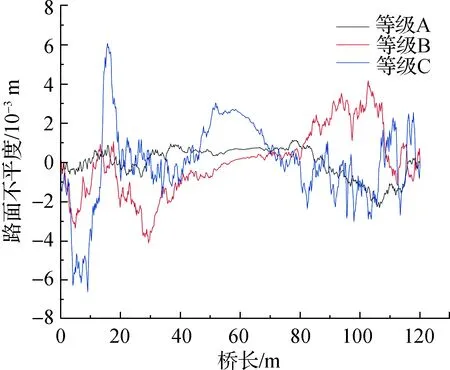
图2 路面不平整样本Fig.2 Samples of road roughness

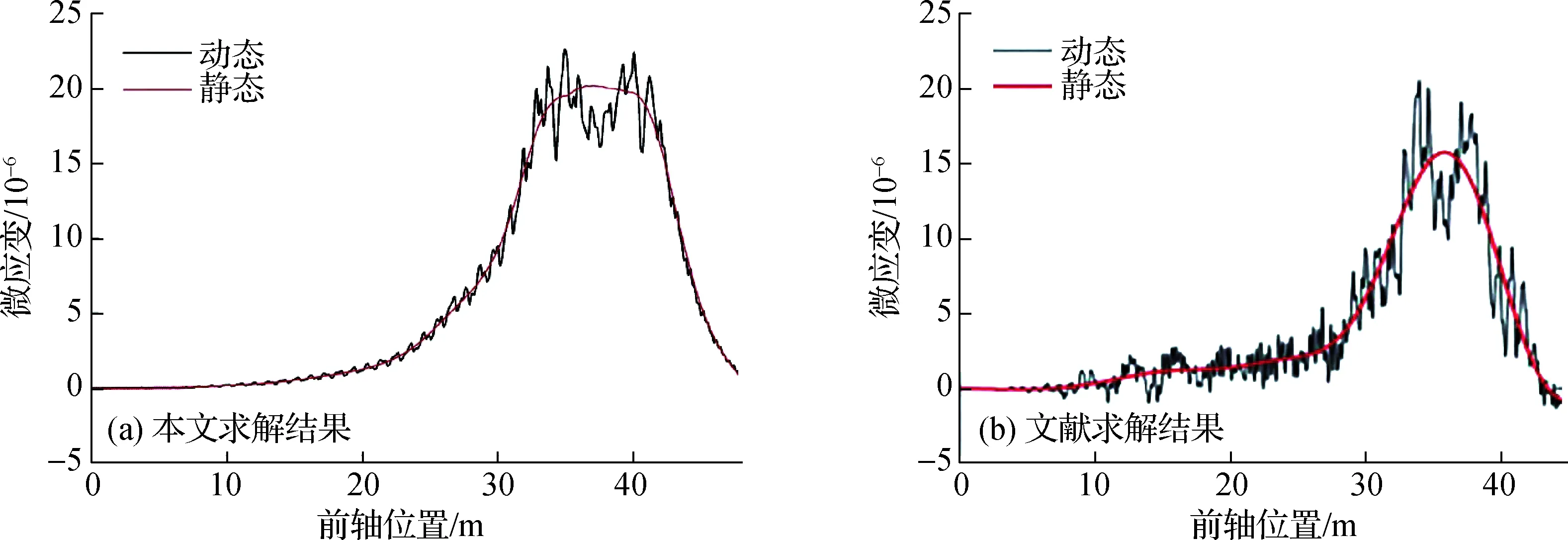
图3 1/4跨截面测点微应变时程Fig.3 Micro-strain time history curve of 1/4 cross section measurement point

2 桥梁概况及有限元分析模型

本文以厦门天圆大桥为工程背景，如图4所示，该桥为跨径120 m的中承式单拱肋拱梁组合体系钢桥，主梁为大宽跨比(0.268)等截面单箱单室钢箱梁，主拱为箱形单拱肋，拱与主梁之间的刚性吊杆为Q345-C钢板焊接变截面矩形钢箱.吊杆上端通过连接板与拱肋耳板采用鞘铰连接，下端通过焊缝与锚座连接，锚座与主梁通过焊缝刚性连接.桥面行车道为双向六车道布置，主梁两侧分别设有3.3 m宽的人行道.选取图4中P1～P8共8个测点作为动力响应的分析位置.拱肋上的P1、P2分别位于1/4跨、1/2跨截面处.箱型主梁底板中点为测点P3，顶板中点为测点P4，测点P5、P6分别位于测点P4两侧.在1#吊杆和7#吊杆分别设置测点P7、P8.

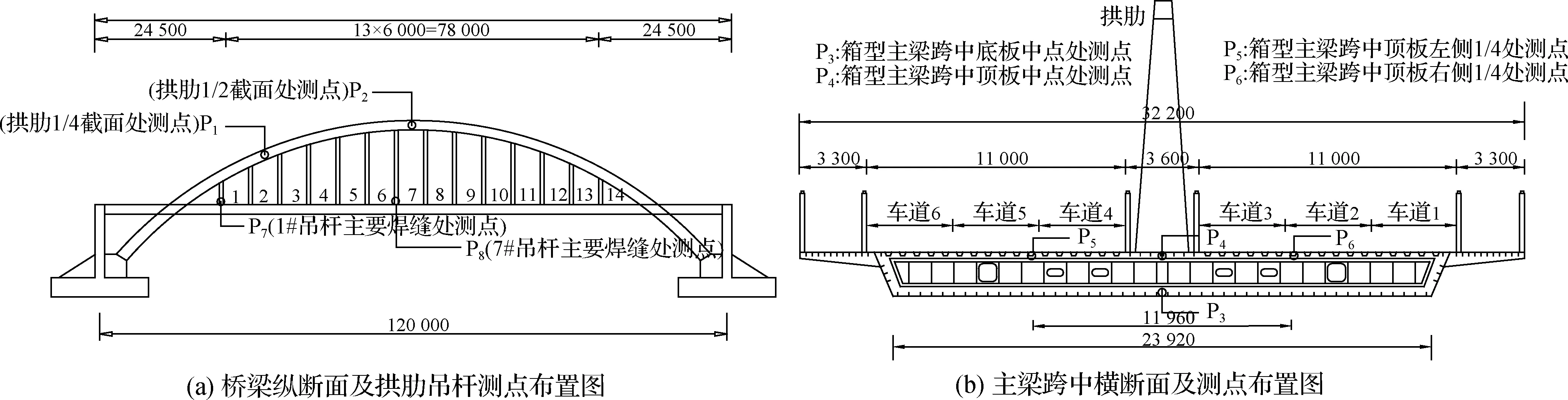
图4 桥型结构及测点布置图(单位：mm)Fig.4 Layout of bridge structure (unit: mm)

根据设计图纸，对该桥进行建模，采用壳单元来模拟箱型主梁及刚性吊杆，采用梁单元模拟拱肋.主梁两端支座位置采用简支约束，拱肋两端采用固端约束.钢材弹性模量取2.06×1011N/m2，泊松比取0.31，材料密度取7 850 kg/m3.全桥划分网格后共计61 312个单元，有限元模型如图5所示.为了验证有限元模型的合理性，取模态分析前3阶结构自振频率，与西安长大公路工程检测中心通过桥梁动载试验测得的模态比较.从表1可见，所建有限元模型与桥梁实际情况基本一致.

图5 天圆大桥有限元模型Fig.5 Finite element model of the Tianyuan Bridge

表1 天圆大桥主要振动频率比较

3 冲击效应影响因素的数值分析

3.1 行车速度的影响

常用的冲击系数主要有位移冲击系数和应变冲击系数，本文采用应变冲击系数，其定义式如式(5)所示：

(5)

其中，Ydmax为在汽车过桥时应变时间历程曲线上的最大应变值；Yjmax为相应的最大静力效应值.本文桥梁的动力响应曲线通过数值模拟分析方法获取，最大静力应变值通过模拟准静态试验获得，即模拟车辆以很低的运行速度(通常<1 m/s)通过桥梁时计算提取.图6为1#短吊杆当HS20-44卡车在3车道过桥(车速45 km/h，C级路面)中的结构响应数值计算结果.

图6 P7测点典型的动力和准静态应变时程曲线Fig.6 Typical dynamic and quasi-static strain time history curves of P7 measuring point

为了分析车速对拱梁组合体系桥梁冲击效应的影响，以C级路面不平整度情况为例，HS20-44车型在车道3分别以30，45，60，75，90 km/h的速度通过该桥，各主要构件的冲击系数计算结果如图7所示.

图7 不同车速下拱桥各测点的冲击系数计算值Fig.7 Calculation value of impact coefficient at each measuring point of arch bridge under different vehicle speed

随着车速的增加，吊杆、拱肋、主梁顶板及底板各测点的冲击系数总体都呈现先增大的趋势，当车速达到45 km/h左右时取得最大值，之后冲击系数随着车速的增加而逐渐减小.这一计算结果与已有文献[13]的结论一致.C级路面下，短吊杆的冲击系数最大达到0.432，长吊杆的最大冲击系数为0.322，短吊杆在车辆荷载作用下会受到更大的冲击效应.拱肋1/2跨截面的冲击系数大于1/4跨截面的冲击系数.主梁顶板及底板的冲击系数较小，其数值在0.097～0.145区间变化，相较于吊杆和拱肋，主梁冲击系数偏小.主梁底板中间位置P3测点的整体冲击系数略大于顶板中间位置P4测点及P5测点的局部冲击系数.车辆行驶在离主梁顶板P6测点近的3车道上，因此P6测点处的局部冲击系数比顶板上另两个测点处大.

3.2 路面不平整度的影响

路面不平整度是车桥耦合振动分析中一个极为重要的影响因素[13].考虑到天圆大桥桥面情况良好，故本文仅选择A、B、C 3种不平度等级进行计算.由3.1节可知，在车辆速度为45 km/h左右时，各构件的冲击系数最大.因此考虑选取HS20-44车型在车道3分别以45，60 km/h的速度通过该桥，以此来分析路面不平度等级对拱梁组合体系冲击效应的影响,计算结果如图8所示.

图8 不同路面等级下的冲击系数Fig.8 Impact factor changing with pavement condition

由图8可见，无论车速为45 km/h或者60 km/h，随着路面状况恶化，各构件的冲击系数均呈现增大的趋势.以1#吊杆测点P7为例，行车速度为45 km/h时，在A级路面下的冲击系数为0.384，在C级路面的冲击系数为0.432，增大了12.5%，可见路面状况的维护对桥梁冲击效应影响至关重要，相关部门应该引起高度重视.

3.3 不同车辆模型的影响

3.1节和3.2节中都是以AASHTO中的HS20-44车型作为计算车型来探讨不同因素对拱梁组合体系冲击效应影响，为了讨论不同车型对冲击系数的影响，与3.1节中的计算对应，补充计算了5axle-CHN车辆模型过桥的工况，路面等级同为C级，该车分别以30，45，60，75，90 km/h在车道3匀速行驶过桥，冲击系数计算结果如图9所示.

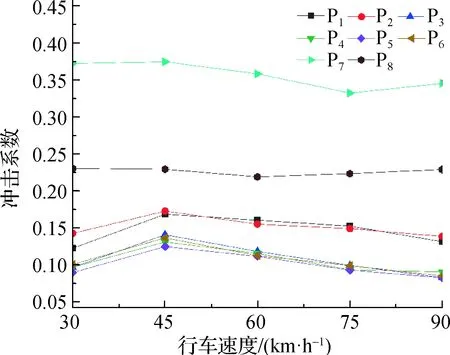
图9 5axle-CHN车型作用下冲击系数随车速的变化Fig.9 Impact factor with the 5axle-CHN model at different traveling speed

比较图7和图9，5axle-CHN车型作用下各构件冲击系数比HS20-44车型行驶过桥产生的冲击系数都要小.例如行车速度为30 km/h时，拱肋1/4截面处测点P1在5axle-CHN车型作用下的冲击系数为0.122，相较于HS20-44车型作用下的冲击系数0.148，减少了17.57%.车轴重、车轴间距、车轮的阻尼及刚度等因素共同影响桥梁的冲击系数[10-11]，且5axle-CHN车型的车辆参数取值尚需进一步确定，不同车型对冲击系数的影响还有待于深入的研究.

3.4 横桥向不同车道加载位置的影响

为了分析在横桥向不同车道加载对拱梁组合体系冲击效应的影响，本节依然选用HS20-44车型，设定车速为45 km/h，路面等级为C级，分别在车道1、车道2及车道3行驶过桥，冲击系数计算结果如图10所示.

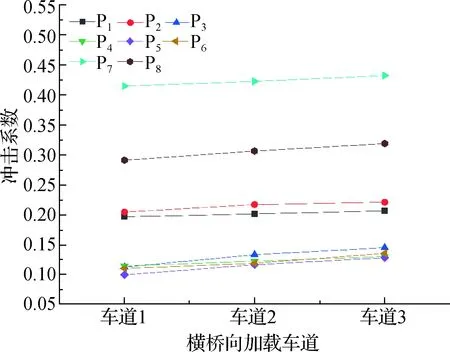
图10 车辆行驶在横桥向不同车道下的冲击系数Fig.10 Impact factor with vehicle passing in different lane

车辆行驶在车道1、2、3时，主梁跨中底板测点P3的冲击系数分别为0.113、0.133、0.145.其他构件的冲击系数变化也呈现相同的变化趋势，车辆行驶在车道3时，与行驶在车道1、车道2相比较，各构件的冲击系数整体上呈增大趋势.偏载对复杂桥梁的挠度冲击系数会产生影响，但偏载并不会使各构件的冲击系数增大，反而当车辆在靠近结构横向中心线的车道上行驶时，各测点的冲击系数最大.

根据车桥耦合振动分析，在3种路面等级下，车速在30～90 km/h时，主梁整体冲击系数介于0.082～0.145之间，拱肋跨中截面冲击系数介于0.122～0.226之间，吊杆的冲击系数介于0.219～0.432 之间.整体上，主梁冲击系数、拱肋跨中截面冲击系数、吊杆的冲击系数依次增大.

4 冲击效应的实测数据对比分析

为了验证数值计算结果的可靠性，本节利用该桥上安装结构振动监测系统，对箱型主梁跨中截面底板中点处P3、拱肋1/4跨截面处P1、1#吊杆主要焊缝处P7的应变测点处采集到的实测动应变展开分析(应变测点布置如图4所示).主梁应变片为顺桥向(考虑主梁以正截面受弯为主)、主拱应变片为拱轴线方向(考虑拱截面以受压为主)、吊杆应变片为杆轴向(考虑吊杆以轴向受拉为主)，应变片接桥方式为1/4桥法，采样频率100 Hz，考虑桥上车辆实际的通行情况，为获取单车过桥的动应变时程，从2019年9月5日零点至9月8日24点的动应变监测时程数据中截取30个样本，结合主桥长和行车速度，样本时长取8 s左右，能涵盖时速30～70 km/h单车过桥的时间，对实测数据进行如图11所示的去噪去漂处理，所截取的实测数据与典型的数值模拟应变时程曲线对比如图12所示，由于车辆、车速不同，时程曲线在数值上存在一定的差别，但总体趋势较为一致.

图11 实测数据去噪去漂处理Fig.11 De-noising and de-bleaching of measured data

图12 单车过桥实测应变与数值计算时程对比Fig.12 Comparison between measurement strain and numerical calculation time history of single vehicle bridge

将30个实测数据样本，根据现场试验常用的波峰-波谷均值法计算得到拟静态应变值，再计算冲击系数，如图13所示.然后与第3节中数值计算得到的冲击系数进行对比，结果如表2所示.可以看出实测样本的冲击系数与有限元模型数值计算结果基本吻合，说明本文对桥梁各主要构件冲击效应的数值分析是合理的.

表2 冲击系数比较

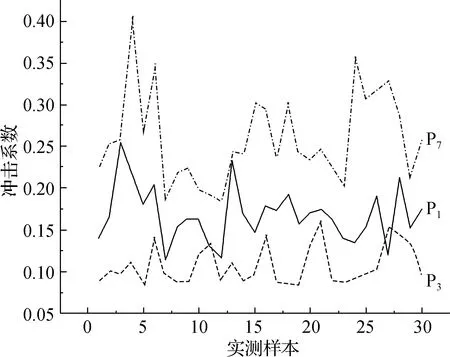
图13 实测样本冲击系数Fig.13 Impact coefficient of measured samples

5 结 论

本文采用三维车桥耦合振动的分离迭代法，针对行车速度、路面不平整度、不同车辆模型、车辆横向行驶位置等因素，对组合体系拱桥的各主要构件开展了冲击效应的差异性分析，得到如下主要结论：

1) 在确定的路面等级下，随着车速的增大，各构件的冲击系数总体呈现先增大的趋势，并在车速为45 km/h左右时取得最大值，之后随着车速的增加而逐渐减小.

2) 随着路面不平度的恶化，各构件的冲击系数均呈现增大的趋势，路面不平度对拱梁组合体系结构冲击系数的影响显著.

3) 车辆模型的不同会对拱梁组合体系冲击效应产生影响，HS20-44车辆模型作用下各测点的冲击系数比5axle-CHN车辆模型作用下大.

4) 车辆横向加载位置对桥梁各主要构件冲击效应有一定的影响，靠近测点的车道上行车会使冲击效应略微增大.

天圆大桥有限元模型计算得出的主梁竖向基频为1.525 Hz，根据《公路桥涵设计通用规范》(JTG D60—2015)，利用该基频计算得到的冲击系数为0.059.车桥耦合振动分析结果表明，对于复杂结构体系桥梁，由规范计算的冲击系数整体偏小，趋于不安全.另外，设计中对于桥梁的不同构件应充分考虑冲击效应的差异性.