基于滑动单元的高速磁浮列车-轨道梁耦合系统的动力相互作用分析

古 泉，袁 彬，国 巍,刘永斗,周惠蒙

(1.厦门大学建筑与土木工程学院，福建 厦门 361005；2.中南大学土木工程学院，湖南 长沙 410075；3.中国地震局工程力学研究所，河北 三河 065201)

高速磁浮列车一直是轨道交通领域的研究热点.磁浮列车相比较传统的高速轮轨列车有着显著的优势： 1) 能耗低； 2) 电力驱动，无废气排放，节能环保； 3) 车体与轨道无接触，安全舒适且轨道损耗小.随着科学技术的不断发展，磁浮列车的时速不断攀升.磁浮列车运行过程中的动力学问题直接影响着列车运行过程的舒适性和安全性.

业内学者关于高速磁浮列车-轨道梁耦合系统的动力仿真分析大多采用以下方法：将磁浮列车的各个构件视为刚体，使用多体动力学方法建立运动方程进行求解[1]，或直接使用商业多体动力学软件如SIMPACK进行建模计算[2]，同时使用软件内置的桥梁模块进行求解；使用多体动力学结合有限元法，对磁浮车辆系统与轨道梁系统分别建立运动方程，通过轨道梁位移计算轨道梁系统对车辆系统的力，求解车辆系统的动力学方程，得出车辆的响应后再根据此响应计算车辆系统对轨道梁系统的力，在时域内积分运算求解计算[3].在使用多体动力学方法求解过程中，由于轨道梁不可视为刚体，导致求解过程不连贯.

本文以TR08型磁浮列车和上海Emsland磁浮轨道梁为例，使用二维滑动单元[4]模拟磁浮列车行驶过程中电磁铁与桥梁之间的连接，并在有限元软件OpenSees中完成磁浮列车与轨道梁的建模仿真.数值模拟全程在OpenSees平台完成.该平台拥有丰富的材料库和单元库，使得考虑更复杂的三维非线性的磁轨相互作用成为可能.

1 适用于电磁作用的二维滑动单元

1.1 二维滑动单元模型

图1为二维滑动单元的示意图，该单元由一个磁浮节点m和列车行进过程中所有可能与之接触的梁单元节点序列构成.在磁浮列车模型中，电磁铁与轨道梁之间的接触关系为电磁力相互作用.

对于二维问题，轨道梁单元仅考虑竖向和转动自由度，磁浮节点仅考虑竖向自由度.因此，该滑动单元自由度和内力可以表示为：

u=[umu2…un-1un]T，

(1)

R=[FmR2…Rn-1Rn]T.

(2)

式中：um是磁浮节点的竖向位移；Fm为磁浮节点竖向内力；u2～un为所有可能与磁浮节点产生相互作用的轨道梁单元的节点位移；R2～Rn为所有可能与磁浮节点产生相互作用的梁单元的节点内力.

如图1所示，在某一时刻t，磁浮节点前进至单元K处时，二维滑动单元a、p、q节点内力和对应刚度取值均为0,i、j节点内力和对应刚度取值不为0.为方便计算推导，将未接触的局部节点a、p、q定义为未激活节点.因此，激活的局部滑动单元自由度和节点内力表示为：

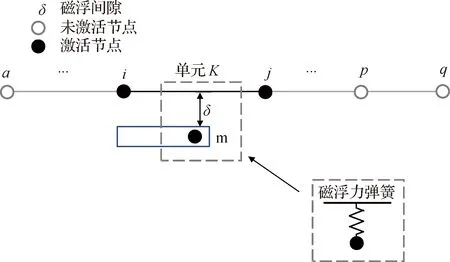
图1 滑动单元模型Fig.1 Model of sliding element

(3)

(4)

如图2所示：u2～u5和R2～R5分别表示局部滑动单元激活节点对应的位移和内力；x为磁浮节点m与激活的轨道梁左节点i之间的水平距离，可通过速度积分求得；L为与磁浮节点连接的梁单元长度.

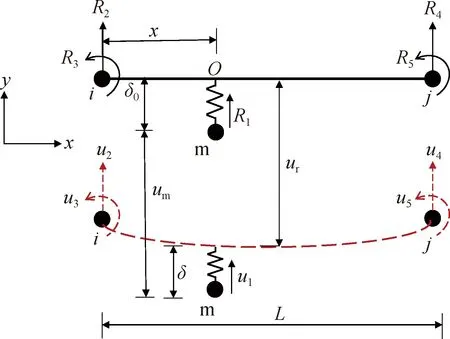
图2 激活的滑动单元的局部节点Fig.2 Local node of active slide element

通过插值得到轨道梁在x处的位移为：

(5)

其中，N为插值形函数，可表示为

(6)

1.2 磁浮力的求解

(7)

悬浮架与轨道梁之间的相互作用力由电磁铁提供.事实上电磁力是空间中的三维分布力，目前尚没有简单的解析表达式.根据电磁学理论[5]，二维情况下，电磁铁的瞬间吸引力为：

(8)

式中,μ0为空气磁导率,N为电磁线圈匝数,A为磁极面积,δ(t)为磁浮间隙,i(t)为通过电磁铁的电流.在磁浮间隙小幅度变化时，根据文献[6]，磁浮力可以等效处理为线性弹簧阻尼力：

(9)

将式(9)稍作变形可得：

(10)

式中：δ和δ0分别为当前磁浮间隙和初始磁浮间隙;Fm0为磁浮列车静悬浮，即δ=δ0时的磁浮力.

根据磁浮力计算式(10)可知，若求解磁浮力，首先要得到磁浮间隙.磁浮节点与轨道梁的连接关系见图2.根据几何关系可以得到：

δ0-um=δ-ur.

(11)

式中：um为磁浮节点位移；ur为磁浮力弹簧连接处轨道梁的位移，包括由形函数插值得到的位移uS和由磁浮力作用产生的额外位移uFm.

ur=uS+uFm,

(12)

(13)

式中，Fflex为梁在x处的柔度，EI为梁单元的抗弯刚度.

根据式(10)，可以得到磁浮力计算公式：

Fm=Fm0+keq(uS+uFm-um)+ceq(vr-vm)，

(14)

式中，uS+uFm和vr分别为磁浮力弹簧连接处轨道梁的位移和速度，um和vm分别为磁浮节点m的位移和速度.

1.3 滑动单元刚度矩阵

根据链式法则，激活的滑动单元的刚度矩阵可写成：

(15)

根据式(7)可以得到激活的滑动单元的节点内力与磁浮力的关系：

(16)

根据式(14)可以得到激活的滑动单元的磁浮力与节点位移的关系：

(17)

根据式(5)有：

(18)

根据式(13)可以得到磁浮力作用下轨道梁的位移uFm与磁浮力Fm的关系：

(19)

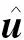
(20)

将式(16)～(20)代入式(15)，可以得到激活的滑动单元的刚度矩阵为：

(21)

2 磁浮列车动力学模型

高速磁浮列车在设计上要求将重力与载荷等尽量均匀地分配到左右两侧的轨道上.通常，磁浮列车的悬挂系统与走行系统在设计和布局上都要求尽可能地与轨道相垂直的纵向中心平面对称.因此,一般可以认为磁浮列车的动力学行为在垂向和横向上是弱耦合的,可以分开处理，以降低问题的复杂度[7].本文以TR08型高速磁浮列车结构为研究对象,参考文献[7]建立TR08型高速磁浮列车单节列车垂向动力学模型,如图3所示.

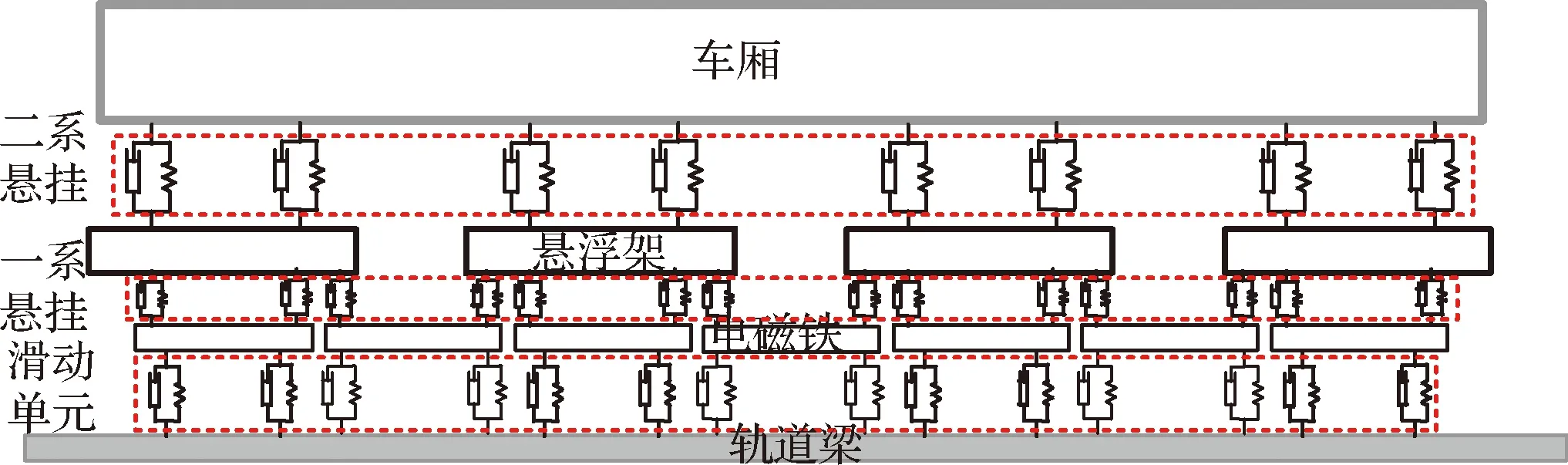
图3 TR08列车垂向动力学模型Fig.3 Vertical dynamic model of TR08 vehicle

TR08型磁浮列车悬浮架结构[8]如图4所示.将磁浮列车车厢、悬浮架、电磁铁都视为刚体.每节车厢下部与4个“H”型悬浮架通过二系悬挂装置连接，每个悬浮架由两个悬浮框和纵梁构成，每个悬浮框由两个C型梁构成.

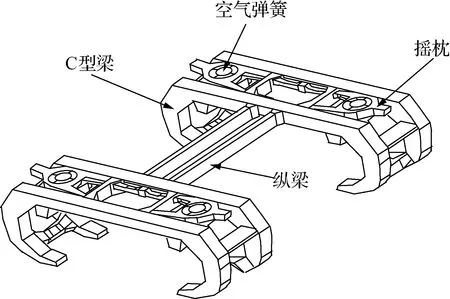
图4 TR08型磁浮列车悬浮架结构Fig.4 Bogie structure of TR08 vehicle

图5为高速磁浮列车-轨道梁耦合系统示意图.车厢与悬浮架之间由空气弹簧、摆杆、摇枕连接，为二系悬挂装置；悬浮架与电磁铁之间由金属橡胶支承连接，为一系悬挂装置；电磁铁与轨道梁之间通过电磁力连接，电磁力主要为电磁导向力和电磁悬浮力.本文中将高速磁浮列车-轨道梁耦合系统简化到二维平面后，系统无平面外位移，电磁力只考虑悬浮电磁铁产生的垂向悬浮力.

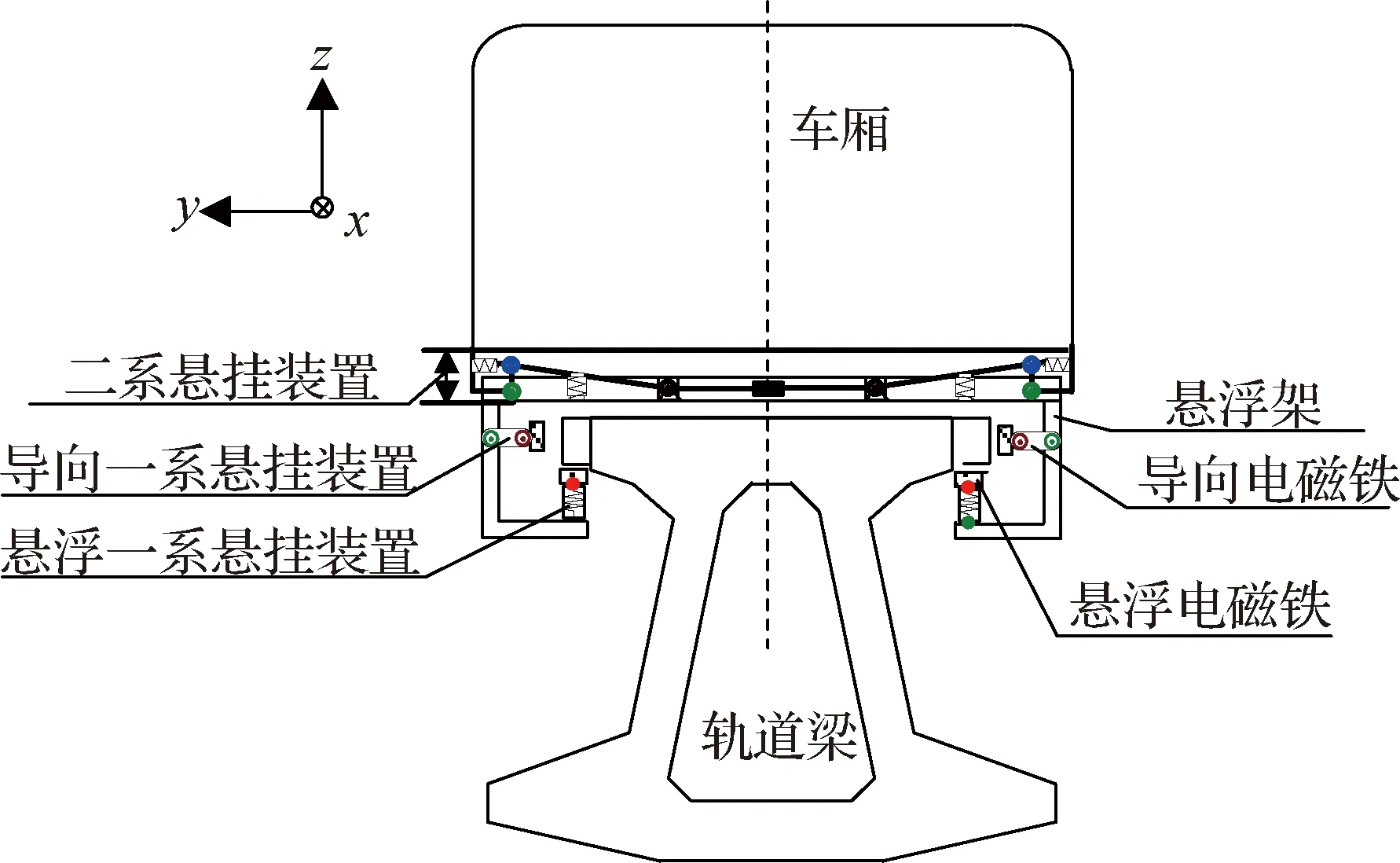
图5 高速磁浮列车-轨道梁耦合系统模型Fig.5 Model of high speed maglev vehicle-guideway coupling system

2.1 二系悬挂系统的等效

将二系悬挂系统简化到二维平面时，需要根据其空间布置进行等效处理.TR08型磁浮列车的二系悬挂系统的剖面图[8]如图6所示.二系悬挂系统可等效看作空气弹簧与摆杆的串联弹簧.而摆杆的刚度大约是空气弹簧刚度的50～100倍，因此在对二系悬挂系统的等效中，摆杆的刚度可以近似忽略.

图6 二系悬挂系统结构剖面图(单位：mm)Fig.6 Sectional view of secondary suspension system of TR08 vehicle (unit:mm)

车体与每个悬浮架之间通过4个空气弹簧装置进行连接.如图7所示，空气弹簧位于x1的位置，车厢通过摆杆与空气弹簧在右边x2的位置连接.等效为二维问题时，以摇枕为对象，忽略其自身重力的作用，对支承转轴处取矩，根据力矩平衡方程有：

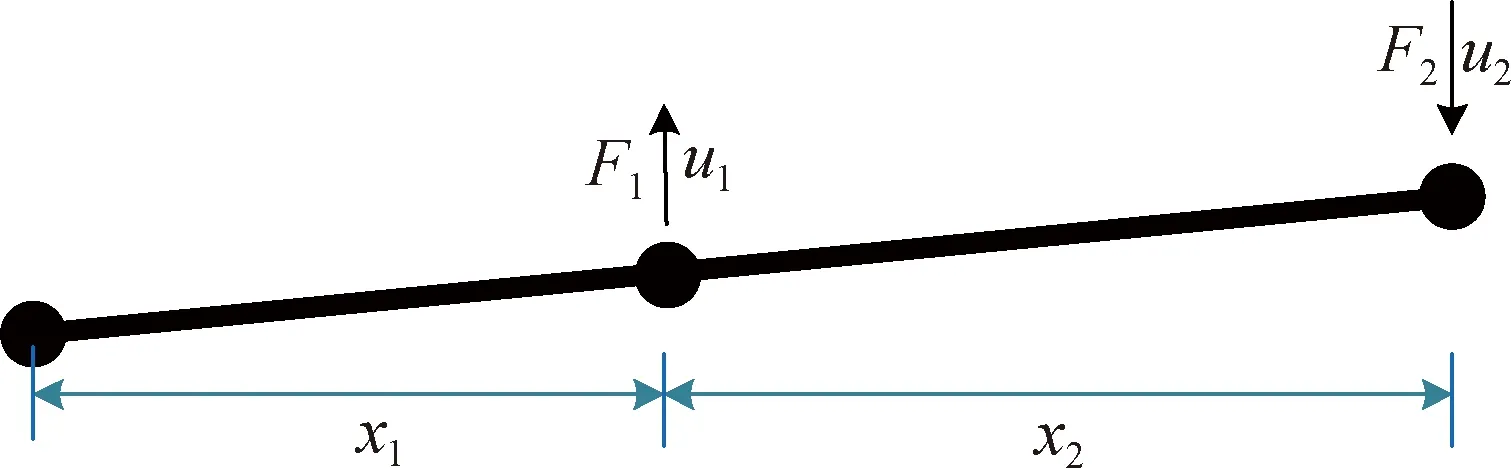
图7 空气弹簧等效示意图Fig.7 Equivalent diagram of air spring

(x1+x2)F2-F1x1=Jα，

(22)

其中J和α分别为摇枕的转动惯量和角加速度.

摇枕转动惯量约为40 kgm2，同时在满足行车舒适度的要求下，摇枕的角加速度很小，故式(22)可近似写成：

(x1+x2)F2=F1x1.

(23)

将摇枕视为刚体，摇枕转动角度很小时，根据位移协调关系有：

(24)

根据式(23)与(24)可得空气弹簧等效刚度：

(25)

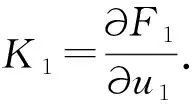
根据式(25)结果可知，等效到二维平面后空气弹簧的刚度不到设计值的1/3，说明该等效措施在建立TR08型磁浮列车二系悬挂系统的二维平面模型时是必要的.

2.2 磁浮列车的数值建模

本文中磁浮力计算使用式(10)中的线性弹簧阻尼模型.磁浮列车参数全部取自文献[2-3,9]，详细参数见表1.

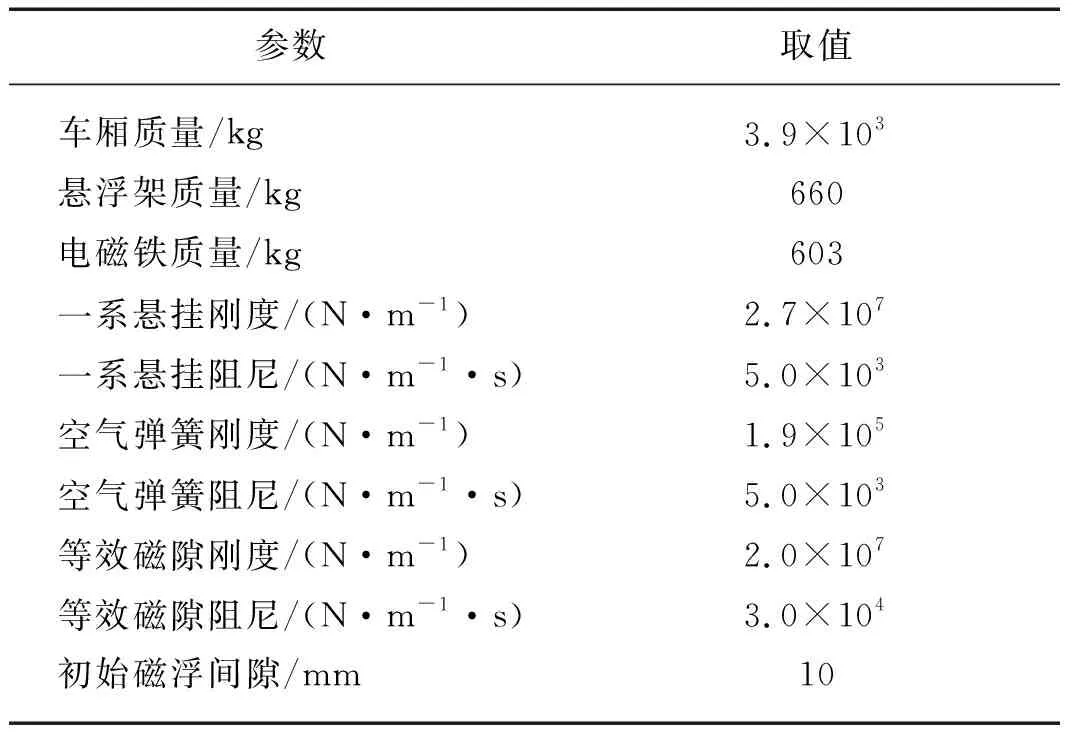
表1 磁浮列车参数Tab.1 Parameters of maglev vehicle

车厢、悬浮架、电磁铁均使用刚性欧拉梁单元模拟.一系悬挂和二系悬挂均使用truss杆单元来模拟弹簧和阻尼.简化到二维平面后，每个一系悬挂在竖向由2个并联的弹簧阻尼单元构成.车体与每个悬浮架间通过4个空气弹簧装置连接.

基于表 1和式(25)中对二系悬挂结构的简化，在OpenSees平台建立了单节磁浮列车的有限元模型，计算得到磁浮列车在竖向二维平面内的第一阶和第二阶自振频率分别为0.797 4和0.846 8 Hz，分别对应于车身在竖向平面内的沉浮和点头运动，对比文献[9]中的数据0.787 8和0.823 5 Hz，说明二系悬挂的简化以及整车模型的建模是正确、可靠的.

3 轨道梁的数值建模

以上海高速磁浮Emsland轨道梁为例，参考文献[10]建立简支梁桥，不考虑桥墩和支座的影响.轨道梁截面如图8所示. 轨道梁的截面形式较为复杂，假定其弹性模量等效于强度等级C60混凝土的弹性模量.根据文献[10]，计算得到轨道梁的截面参数，如表2所示.

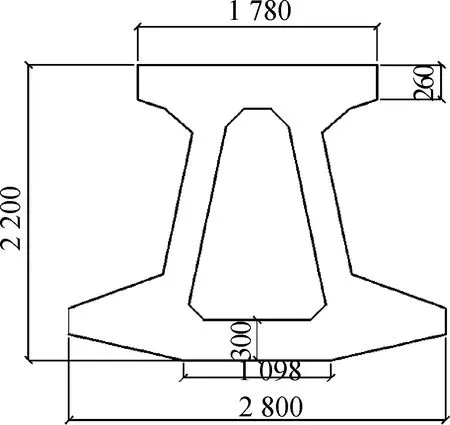
图8 轨道梁截面尺寸(单位：mm)Fig.8 Cross-section dimension of guideway (unit:mm)

表2 轨道梁参数Tab.2 Guideway parameters

在OpenSees平台中使用欧拉梁单元建立单跨简支轨道梁，计算得轨道梁的自振频率.其中简支轨道梁弯曲的一阶自振频率f1的横向和竖向弯曲频率分别为6.33和7.47 Hz.

轨道梁的截面设计还应避免在磁浮列车行驶时产生共振.对于简支轨道梁，f1需满足以下要求[11]：

(26)

式中,v为列车行车速度,L为轨道梁的跨度.

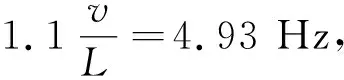
4 数值验证

在OpenSees平台建立TR08磁浮列车-轨道梁系统的二维平面模型，使单节磁浮列车以400 km/h匀速通过单跨长24.768 m的简支梁桥.图9为高速磁浮列车驶过简支轨道梁时，轨道梁跨中的挠度时程曲线和加速度时程曲线.可以看出跨中加速度在-0.39～0.60 m/s2之间波动；跨中最大挠度为2.76 mm，小于跨长的1/4 000，符合规范要求[8].

图9 跨中挠度(a)和加速度(b)Fig.9 Mid-span deflection (a) and mid-span acceleration (b)

图10为磁浮列车通过桥梁时车体质心的加速度时程曲线.为满足行车舒适度要求[11], 磁浮列车的加速度需满足要求：竖向的向上加速度≤0.5 m/s2，向下加速度≤1.0 m/s2.图中车身竖向加速度在-0.018～0.017 m/s2之间，满足行车舒适度要求.

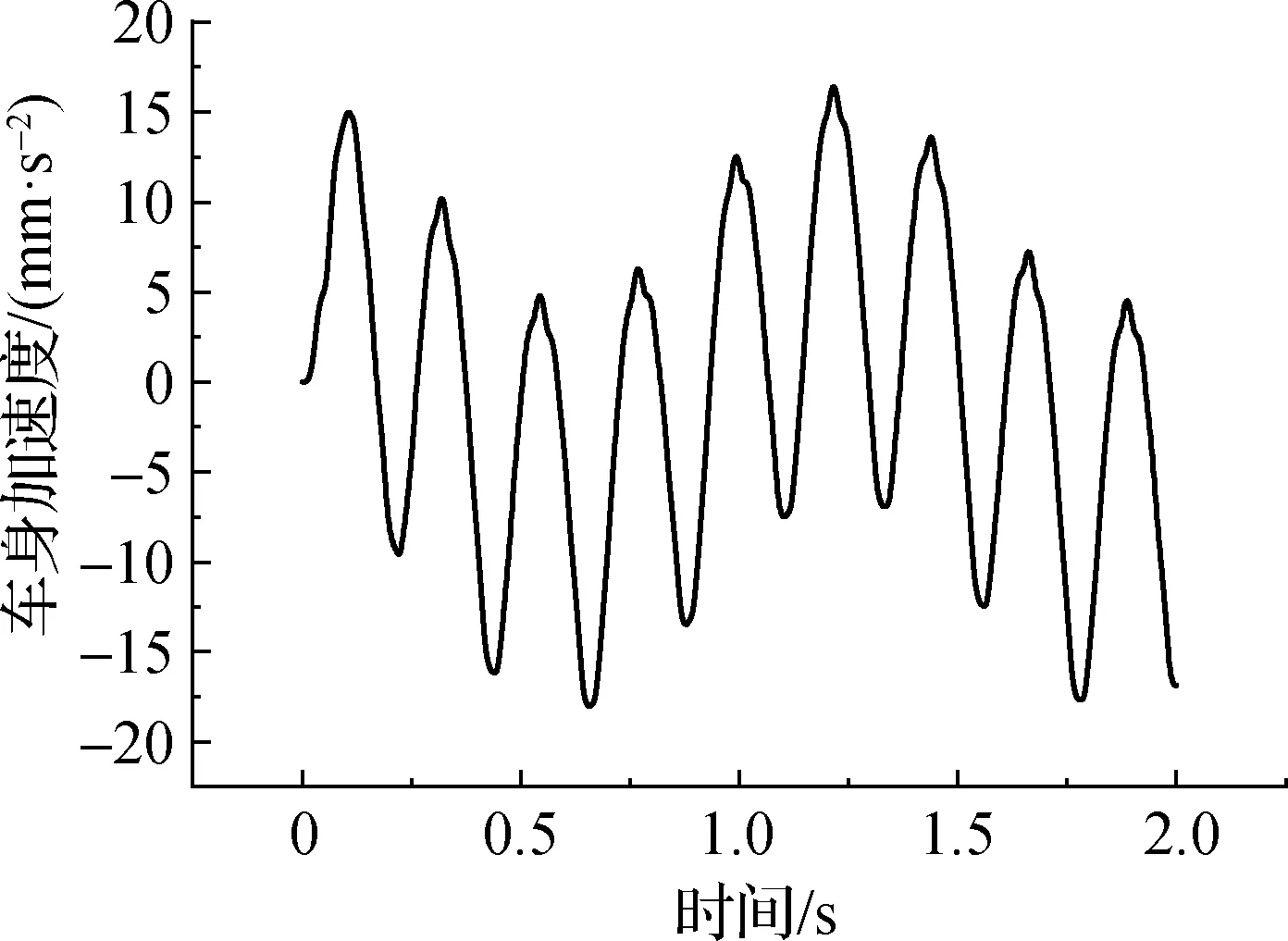
图10 车体质心加速度Fig.10 Acceleration at centroid of carbody

图11为磁浮间隙的变化时程曲线，从图中可以看出磁浮间隙的波动范围为-0.21～0.17 mm之间，满足±2 mm的要求[12]，说明本文中将二维磁轨作用力等效为线性弹簧阻尼力是合理的.

图11 磁浮间隙的变化幅值Fig.11 Variation amptitude of maglev gap

5 结 论

本文推导了将磁浮力等效为线性弹簧阻尼力时

滑动单元的刚度矩阵，并在有限元软件OpenSees平台中实现.建立了TR08型磁浮列车与上海Emsland磁浮轨道梁的二维有限元模型，计算得到磁浮列车以400 km/h高速通过轨道梁时的列车与轨道梁的动力响应.结果均满足规范要求，并与文献中结果进行对比，验证了模型的可靠性.可以用改进后的滑动单元模拟电磁铁与轨道梁间的相互作用，以计算分析更复杂的高速磁浮列车-轨道梁耦合系统问题.