金属基复合材料界面与内聚力模型的研究进展

张泽文 潘永智 张天一 付秀丽

（济南大学机械工程学院，济南 250022）

文 摘 首先对金属基复合材料的界面物相组成和检测、结合强度等方面的研究进展进行综述，基于传统断裂力学，对现有金属基复合材料界面相进行表征的内聚力模型进行分析，探讨了内聚力本构关系及参数获取方法，并对模拟仿真在金属基复合材料界面相中的应用进行了总结，提出了未来研究的重点和方向。

0 引言

轻量化高端装备及关键基础构件的高性能、高可靠性要求带动了金属基复合材料产业的不断创新和飞速发展［1-3］。金属基复合材料由金属基体相、增强相以及界面相组成，能够保持各组分材料的优点，克服单一材料的缺陷，在航空航天、军事等领域［4-6］应用广泛。由于金属基复合材料由多相材料组合而成，属于典型的难加工材料，且基体相与增强相间形成具有明显性能差异的界面层是金属基复合材料的特点之一。在金属基复合材料的切削加工过程中，常规宏微观检测方法得到的界面层组织和性能特征，与实际仍有明显差距，其界面层的结构和性质很难被准确把握。因此，在金属基复合材料的微观有限元仿真模拟过程中，界面层的缺失或不够准确是模拟仿真结果相较于实际产生较大误差的主要原因，限制了其仿真精度的提高。同时，用来分析传统单相均质材料的传统断裂力学，如线弹性断裂力学，已经无法满足金属基复合材料界面脱粘及粘结界面开裂等研究需求，基于弹塑性断裂力学的内聚力模型逐渐发展完善，能够应用于进行上述计算过程并得到较为精确的结果。因此，研究金属基复合材料界面，对其界面裂纹扩展的内聚力模型进行准确表征和描述及研究金属基复合材料的界面层特征和进行切削有限元模拟、切削加工机理研究均有重要的理论意义和工程价值。

本文首先对金属基复合材料的界面物相组成和检测、结合强度等研究进展进行综述，基于传统断裂力学，对现有金属基复合材料界面相表征的内聚力模型进行分析，探讨了内聚力本构关系及参数获取方法，并对模拟仿真在金属基复合材料界面相中的应用进行了总结，提出了未来研究的重点和方向。

1 金属基复合材料的界面特征

物理意义上，金属基复合材料的界面相是指基体相与增强相之间的结合部，与力学模型意义上含义不同［7］。金属基复合材料的界面不是一个理想的平面或曲面，而是存在于基体与增强相之间化学成分有显著变化的、构成彼此结合的、具有复杂力学行为的微小过渡区域。基体相与增强相两相间的线胀系数失配，会造成残余应力不匹配，进而影响金属基复合材料受载时的力学行为，如造成材料拉伸和压缩性能的明显差异等［8］。金属基复合材料界面脱粘（图1）［9］是工件失效的主要形式，界面相的结构与性能对金属基复合材料整体的性能有极大的影响。

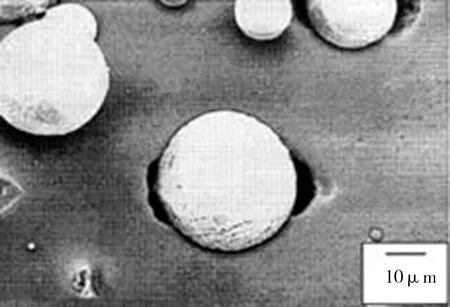
图1 颗粒增强金属基复合材料界面脱粘［9］Fig.1 Interfacial debonding of particle reinforced metal matrix composites［9］

1.1 界面物相组成与检测

金属基复合材料界面层的物相组成是研究界面层的重要内容，其物相组成及检测综述如表1所示。QIAN 等［10］使用透射电镜及高分辨率透射电镜针对SiCp/Al 金属基复合材料的界面相进行研究，并使用EDS 对界面元素进行扫描发现Al 基体相与SiC 颗粒增强相之间的界面相是一条非晶态SiO2带，含有微量的Si、C 及Al 元素，并且这些元素来自于基体相与增强相的扩散。刘侃等［11］基于自制Fe-Ti 金属黏结剂与ZTA 陶瓷颗粒制备金属基复合材料，通过微观分析金属基复合材料的界面行为，发现较高含量的黏结剂界面结合，能够较好地保持复合材料的结构和尺寸，且增强相与基体相的结合界面无明显缺陷，证明了TiOx过渡层起到了改善界面的作用。李欢等［12］通过SEM、XRD 等对W5Mo4Cr4V3/42CrMo 金属基复合材料的界面相展开研究，确定了界面区域厚度，且界面区域的减摩性优于增强相与基体相。刘志军［13］针对Al2O3（p）-NiCrBSi 金属基复合材料的界面相进行分析，发现由于元素的扩散运动，金属基复合材料的界面相附近会出现等温凝固现象，形成α-Ni固体层，靠近基体的一侧会渗出Fe-Cr-B 物相，强化了复合材料的耐磨性能。宋静雅［14］认为界面反应为热动力学过程，可在复合材料制备的任何阶段产生，在SiCp/Al 制备过程中界面相会产生中间相Al4C3及Al4SiC4，由于其为一种脆性相，将导致界面相强度以及耐腐蚀性能的降低，从而影响复合材料整体性能。

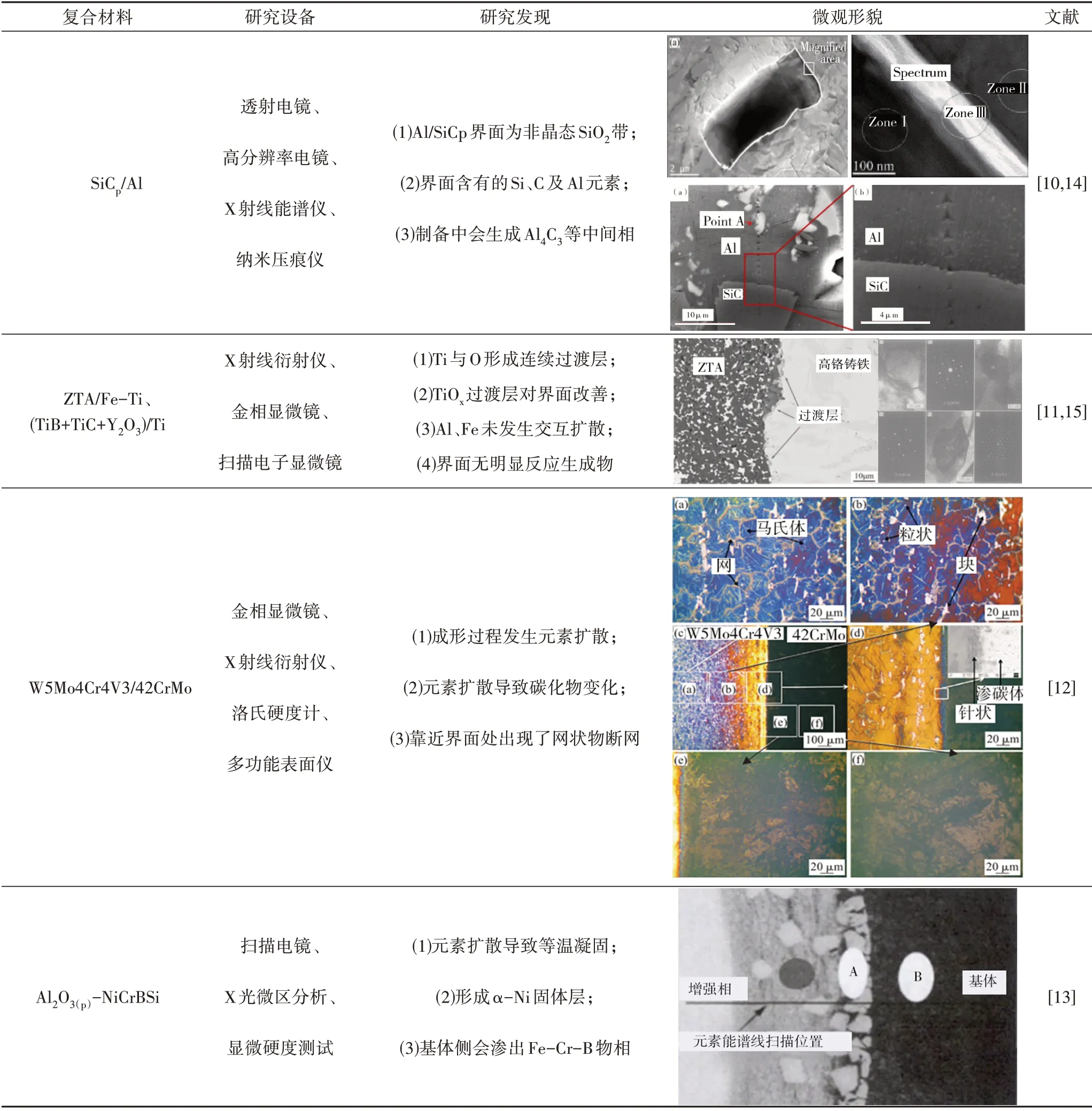
表1 金属基复合材料界面物相组成及检测综述Tab.1 Review on phase composition and detection of interface of metal matrix composites

1.2 界面结合强度

针对金属基复合材料界面层的结合强度，国内外学者进行了大量的试验研究。J.D.ACHENBACH等［16］用连续牵引力和界面间位移差与共轭牵引力之间的线性关系来模拟增强相与基体相间的界面力学行为，并使用模型构建比例常数表征界面的刚度和强度，分析了界面裂纹的萌生、扩展和止裂过程，发现界面参数对金属基复合材料整体弹性模量的影响及界面裂纹发展前后的影响。巴颖等［17］针对碳纤维增强的5056 铝合金金属基复合材料进行纵/横向拉伸试验研究，通过对宏观拉伸应力应变曲线及断口形貌（图2）进行分析，发现其主要失效行为：横向拉伸为纤维-基体界面处剥离，纵向拉伸为界面相的脱粘，从而判断该材料的界面相为中等结合强度。

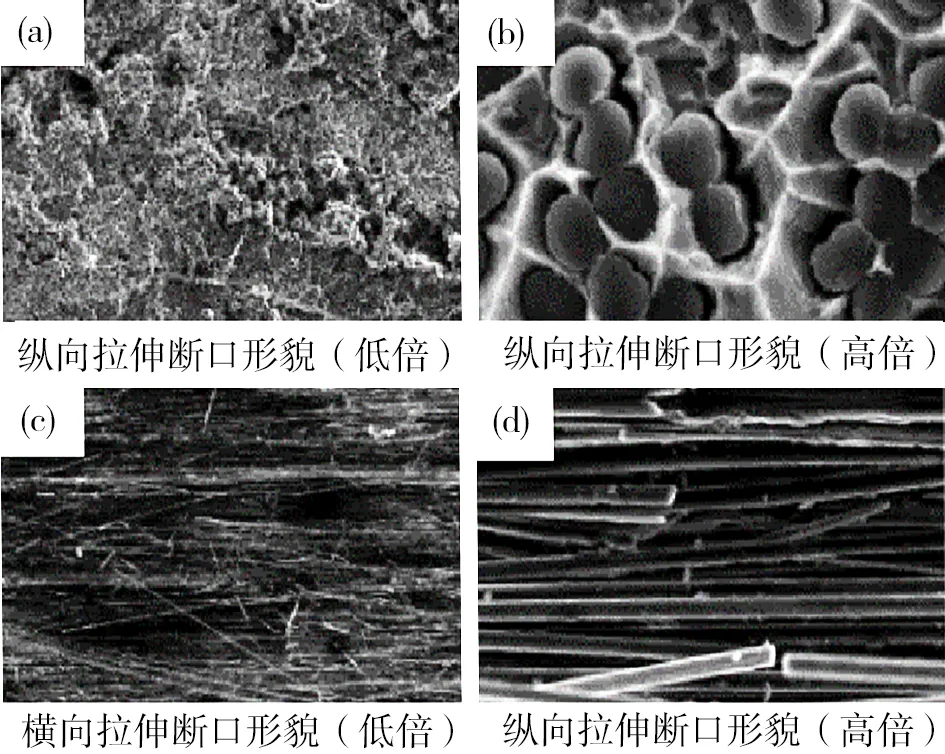
图2 Cf/5056Al复合材料拉伸断口形貌［17］Fig.2 Tensile fracture morphology of Cf/5056Al composite［17］

不同体积分数的颗粒增强型金属基复合材料，结合强度及性能也明显不同。SAURABH TIWAR等［18］对10vol%SiC 颗粒增强金属Al基复合材料的力学性能进行研究（图3），疲劳断口显示T6 合金中有韧窝形成，推测在界面上有韧性断裂和脱粘现象。裂纹通常在界面处萌生，并随循环加载而扩展，最后裂纹合并导致失效。在LM13 复合材料中，界面的脱粘是疲劳破坏的主要机制。在循环加载期间，裂纹在界面处萌生并扩展至失效。王振兴等［19］考虑增强相与基体相之间的润湿性较差，认为增强相的种类与形状及增强相在基体分布状态，增强相与基体相在界面处发生的反应都会对界面结合强度产生影响，以至于对金属基复合材料的力学性能产生影响。宋静雅［14］进行了SiCp/Al金属基复合材料的纳米压痕实验，在微纳米尺度对颗粒增强金属基复合材料界面微区力学性能分布规律及其影响因素展开研究，发现相比于其他研究手段，纳米压痕技术可以较好地表征金属基复合材料界面相残余应力引起的塑性变形区及复合材料基体相的强度，从而评价金属基复合材料的综合性能。但由于其研究仅针对界面塑性变形这一个影响因素展开研究，与生产实际的多影响因素的综合工况差异较大，其研究结果具有一定的局限性。饶紫馨等［20］基于分子动力学实验发现增强相可以提升基体相的拉伸强度和弹性模量，并认为其强化机制主要是剪切滞后强化机制及热失配强化机制。金属基复合材料中的增强相通过界面剪切力传递分担载荷，并由于增强相的与基体相的线胀系数差异较大，增强相周围会产生高强度位错阻碍晶体滑移，使得强度提高。

图3 断口显示界面脱粘失效［18］Fig.3 Interface debonding failure from fracture surface［18］

2 基于断裂力学的材料界面力学模型研究

界面断裂力学的发展对金属基复合材料界面层的研究提供了重要的理论依据。断裂力学分为线弹性断裂力学和弹塑性断裂力学两部分，其主要研究裂纹固体裂尖的应力场和应变场，并分析裂纹扩展的条件和规律。其中，裂纹裂尖前沿的应力场的一般形式可表达为：

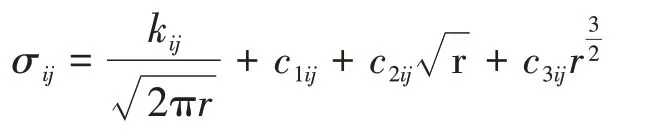
式中，σij为应力分量，r为距裂纹尖端距离，cij为弹性常数。当考虑裂尖附近的区域时，即当r较小时，可只考虑其支配项（奇异项），即其第一项。这样，根据裂尖附近的应力状态，可以将断裂类型基本分为三类：张开型、滑开型和撕开型（图4），任何的断裂形式都是由这3种基本断裂类型叠加得到。

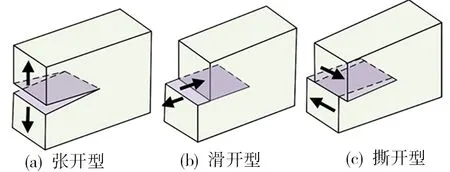
图4 3种基本断裂模式示意图Fig.4 Schematic diagram of three basic fracture modes

2.1 线弹性断裂力学理论

界面裂纹研究最早基于线弹性断裂力学，其假设裂纹体为理想的线弹性材料，使用弹性力学的线性理论对裂纹体进行力学分析。A.A.GRIFFITH［21］对脆性材料的实际强度进行研究，提出了格里菲斯脆性破坏准则，当裂纹尖端区释放的能量达到形成裂纹面积所需的能量时，无需继续增加载荷，裂纹就会发生失稳扩展即自持续断裂的裂纹扩展平衡论。

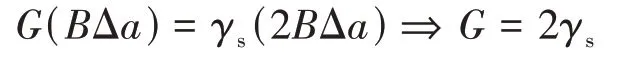
式中，G为应变能释放率，B为裂纹厚度，a为裂纹长度，γs为材料的表面自由能。Griffith脆性破坏准则只适用于纯脆性材料的断裂问题，而金属基复合材料中的金属基体相存在裂纹尖端塑性区使格里菲斯脆性破坏准则失效。针对于金属材料裂纹扩展的问题，E.OROWAN［22］对Griffith 公式进行了修正，裂纹扩展时释放的能量在提供裂纹形成新自由表面所需的表面能同时还要提供裂尖产生塑性区所需的塑性形变能。G.R.IRWIN［23］通过对裂尖附近的应力场的研究，提出应力强度因子K的概念。

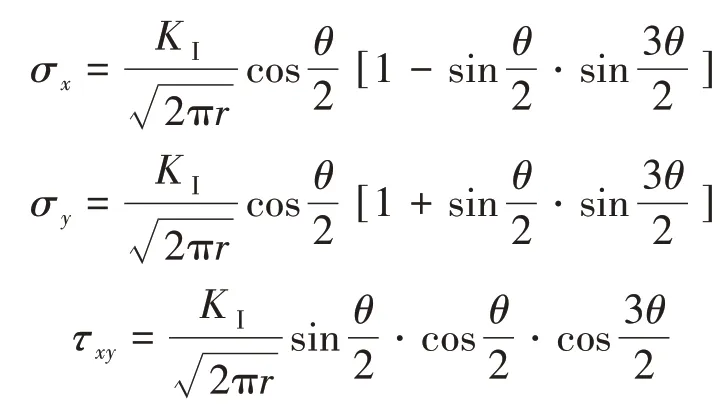
式中，σx，σy，τxy为应力分量，r，θ表示裂纹尖端附近点的极坐标，KⅠ为Ⅰ型裂纹尖端应力场强度因子。基于此，陈路平［24］等针对复合材料界面失效问题进行研究，根据参数变分原理利用参数拟二次规划有限元法对增强相和基体相间的界面失效过程建立了非连续线弹性模型，计算分析了复合材料界面失效问题，并将数值结果与扫描电镜观察到的实验现象进行了对比，一致性较好。但实际上界面相失效力学行为较为复杂，涉及众多材料参数及变形机制仍需要进行研究。

2.2 弹塑性断裂力学理论

在金属基复合材料界面层裂纹尖端通常存在较大的塑性屈服区，线弹性断裂力学理论只适用于同等数量级塑性区较小的情况，对于具有较大塑性屈服区的问题，需要对界面裂纹尖端的奇异应力场进行研究，并以此为基础对界面的断裂行为进行评价。A.A.WELLS［25］提出了弹塑性条件下裂纹的起裂准则即COD 准则，裂纹顶端的张开位移COD 可作为强烈变形的尺度表征裂纹尖端应力应变场的综合效应，但由于其没有明确的物理意义，很难像应力强度因子K一样直接作为应力应变场的表征参量。J.R RICE［26］在此基础上提出J积分，使用围绕裂尖的与路径无关的回路线积分作为表示界面裂纹尖端应变集中特性的平均参量从而回避直接计算裂纹尖端的弹塑性应力应变场，在线弹性情况下有：

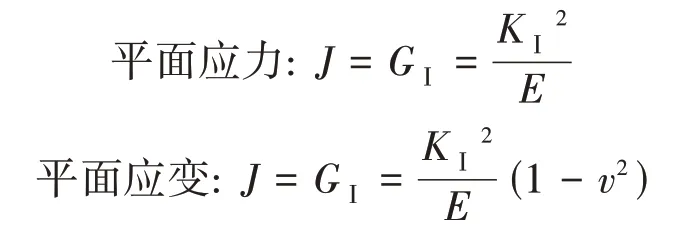
式中，J描述裂纹尖端区域应力应变场的强度，KⅠ为Ⅰ型裂纹尖端应力场强度因子，GⅠ为裂纹扩展能量释放率，v为泊松比，E为弹性模量。进而建立J积分断裂准则：当围绕裂纹尖端的J积分达到临界值时，即J=Jc时，裂纹开始扩展。但J积分不能被用来表征提供新的界面裂纹表面能和裂尖前沿形成新的塑性域所需的能量，因此J积分对于金属基复合材料界面层的表征适用性较差。J.W.HUTCHINSON［27］发表了I 型裂纹尖端应力应变场的弹塑性分析即HRR 奇异解，证明了J积分唯一决定裂尖弹塑性应力应变场的强度也具有奇异性。然而HRR理论考虑了界面塑性变形则必然引起界面裂纹尖端的钝化，裂纹尖端不应该是奇异的。李明瑞［28］提出了一种线性硬化模型，可较好地按等效弹性材料分析界面应力场，但在奇异应力场支配区较小时，会使数值解与理论解产生较大的差异。从力学的角度看，界面的失效行为是一个裂纹在多相介质中的扩展行为，弹塑性断裂力学对界面失效过程的数值模拟存在相当的困难。

2.3 内聚力模型

内聚力模型基于弹塑性断裂力学，认为在裂纹的尖端区域存在一个微小的内聚力区，可以较好地对金属基复合材料的界面相进行分析并对其断裂机理进行评价。D.S.DUGDALE［29］提出一种允许直接计算屈服程度作为外部载荷的函数模型。当在垂直于切口的方向上加载同向载荷时，可以预测屈服现象将被限制在沿着切口的非常窄的带状区域即裂纹尖端塑性区之中。DUGDALE 认为，裂纹端部产生塑性区之后，可以用一个等效裂纹所代替，并采用类似内聚力模型，研究了裂纹尖端屈服和塑性区尺寸的大小；在早期关于非线性断裂的研究中，当内聚力尺寸小于裂纹和试样尺寸时，内聚力理论与Griffith 的能量平衡理论等效。Dugdale 将内聚应力的分布在数值上等同于材料的屈服强度，但从物理角度判断则与实际存在误差。

1962年，G.I.BARENBLATT［30］提出“内聚力模型”，线弹性断裂力学假设裂纹尖端的曲率半径为零，引起了裂纹尖端应力的奇异，实际上裂纹尖端的应力不可能是无穷大，因此他假设裂纹尖端存在一个很小的内聚力区（图5），为裂纹尖端内聚力区示意图；相较于弹塑性断裂力学，内聚力模型不需要材料或结构中包含预置的裂纹，使其在数学模型上能够一直保持连续性条件，使开裂过程中的应力变为开裂位移的函数，从而有效避免了裂纹尖端奇异性。内聚力模型虽然略显粗糙，但因其能准确地计算界面开裂路径上的裂纹萌生与扩展过程，在金属基复合材料界面相方面良好的实用性而得到广泛关注。

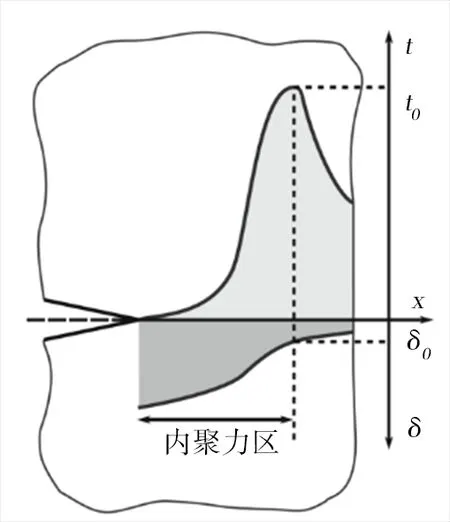
图5 裂纹尖端的内聚力区［31］Fig.5 Cohesive zone at the crack tip［31］

3 内聚力本构关系及参数获取方法

3.1 内聚力的数学模型

由于内聚力模型良好的适用性，学者在D-B 模型的基础上进行了大量的研究，提出了多种内聚力模型，如表2所示。Y.MI 等［32］基于界面单元的使用及应力与相对位移之间的关系，将应力-位移曲线的面积与临界断裂能相结合，建立了典型的双线性内聚力模型（图6），与传统断裂力学相比，其不需预置界面初始裂纹缺陷，可通过算法路径追踪技术自动追踪裂纹萌生与扩展过程并将其与非线性自适应网格技术相结合，在金属基复合材料界面相计算中不断细化，提高结果精准度。

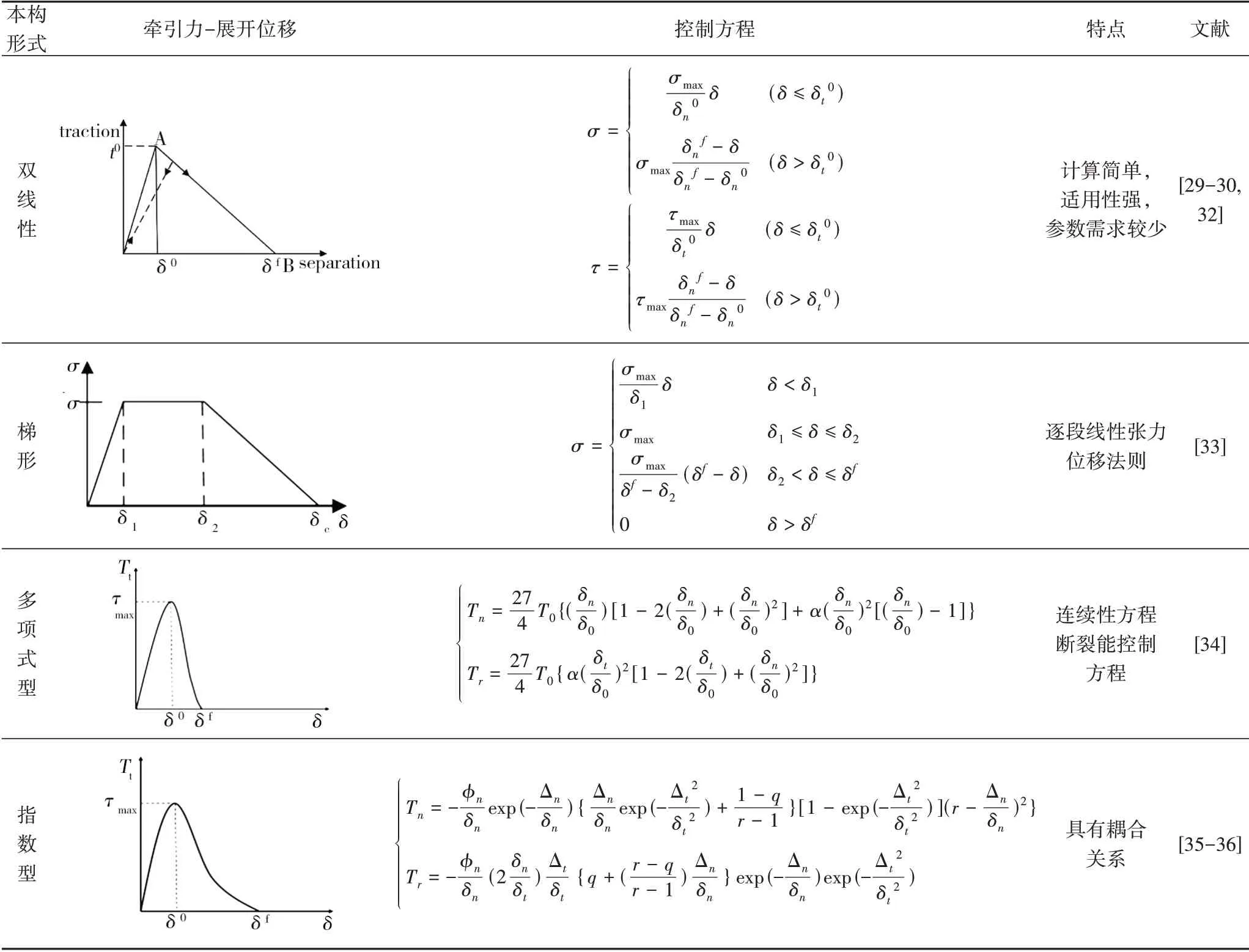
表2 常见的内聚力模型Tab.2 Common cohesive models

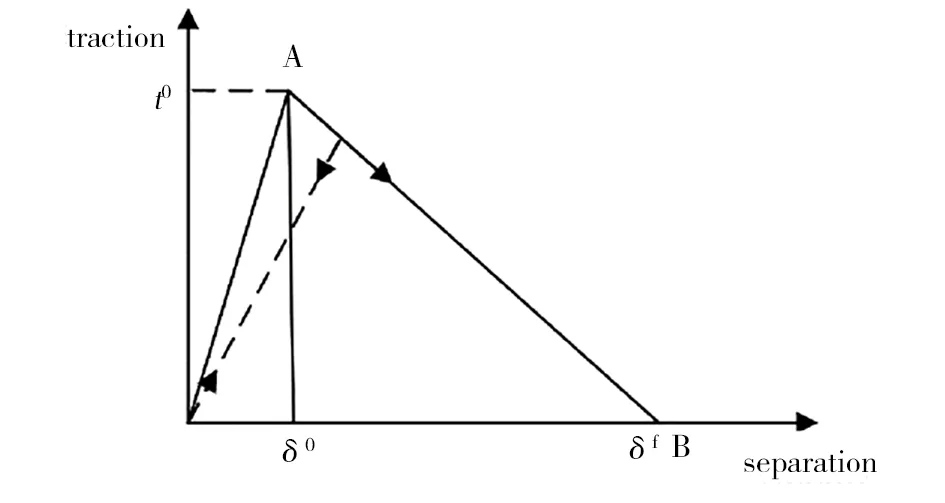
图6 典型的双线性牵引力-位移法则示意图Fig.6 Schematic diagram of typical bilinear traction force-displacement law

图6可知，裂纹尖端牵引力在载荷作用下，对位移的增加呈现线性增长的趋势，当位移达到临界值δ0时材料损伤开始，裂纹萌生并扩展，随后伴随位移的增加t呈现线性降低的趋势减小至零，界面在该处开裂失效。双线性内聚力模型在计算过程中参数较少，便于应用于有限元等场景进行计算求解。

V.TVERGAARD 等［33］针对弹塑性固体，建立了梯形内聚力模型，基于此计算了具有理想牵引力的弹塑性固体在裂纹面上的裂纹初始扩展及阻力，对断裂过程进行了表征。与双线性内聚力模型不同的是梯形内聚力模型认为复合材料据位移发生的最大牵引力不是一个值而是一段区间（δ1到δ2）。A.NEEDLEMAN［34］通过基于高次多项式函数建立多项式内聚力模型，此模型适用于球体夹杂的脱粘问题，针对颗粒增强金属基复合材料界面相的裂纹扩展问题提出了较好的模型方案。在此基础上，A.NEEDLEMAN［35］首次提出了指数内聚力模型，应用于模拟界面裂纹萌生扩展至界面开裂。X.XU 等［36］在此基础上针对指数内聚力模型进行了改进，对界面取向对裂纹扩展路径的影响进行了研究，并对不同取向的裂纹扩展路径进行了分析，由于该种内聚力模型及其导数具有连续性，能够在法向压缩时自动满足接触关系，法向与切向内聚力相互耦合［37］等优点而在金属基复合材料界面失效的预测方面具有良好的适用性。

3.2 内聚力模型参数获取方法

内聚力界面模型参数的取值是进行有限元仿真计算的难题与关键，K.ARK 等［38］利用拉伸试验和三点弯曲实验估算材料内聚力模型参数，对材料的断裂过程进行预测，并通过对比试验对内聚力模型的参数进行了验证。HAN等［39］基于实验估算材料断裂过程中的能量释放率，以这一反应材料断裂性能的特征参数带入到多项式内聚力模型中，确定了内聚力模型参数，但仍不准确。由于实验方法及条件等的局限性，内聚力模型参数较难通过直接实验的方式进行精准获取，目前对于界面参数的确定多基于文献与经验的估计，但此种方法得到的模型参数往往不够精确（图7）。封涛等［40］在Hooke-Jeeves 的参数反演方法的基础上，对典型的双线性内聚力模型参数进行了反演分析确定了界面参数。王效贵［37］等针对内聚力模型参数的确定问题，提出了一种基于Nelder-Mead（N-M）算法的反演化优化方法，以裂纹尖端局部区域内参考点的实测位移信息与有限元计算得到的位移信息建立优化目标函数，实现了对内聚力模型参数的反演识别并对其进行了验证。

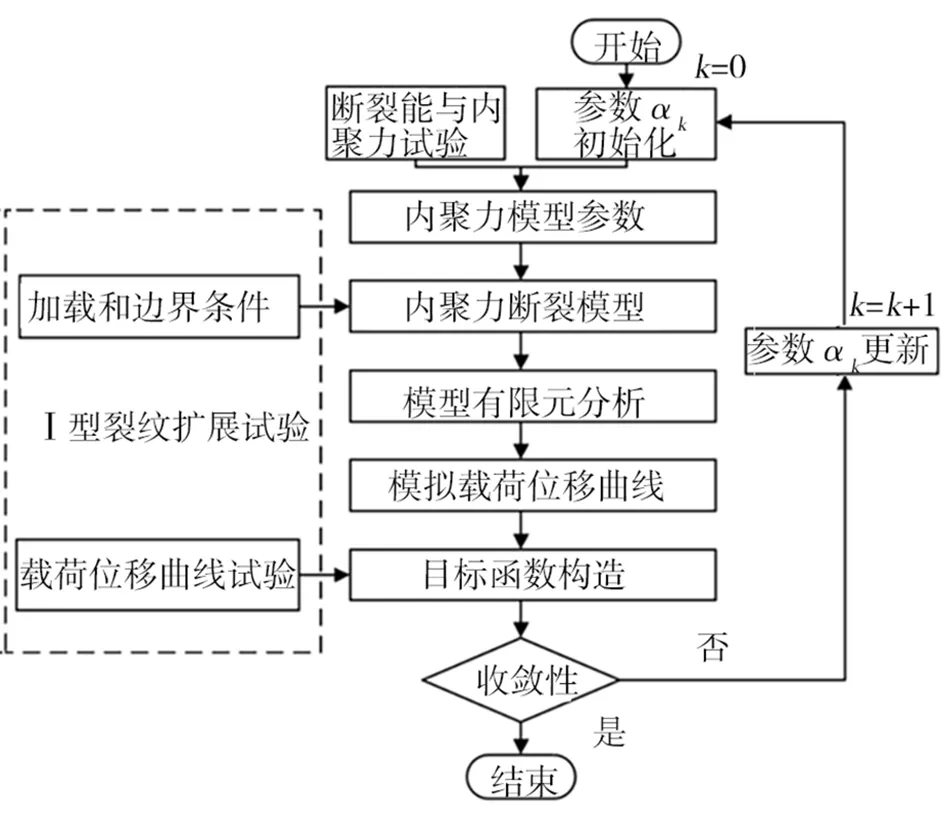
图7 反演方法模型图［39］Fig.7 Inversion method model diagram［39］

4 模拟仿真在金属基复合材料界面的应用

4.1 界面模拟仿真

由于金属基复合材料非均质、多相耦合特征，增强相与金属基体相均会对界面层产生影响，多因素考量金属基复合材料界面层的试验较为困难且周期较长，而采用有限元分析的方法可以更为细致地模拟预测材料界面层状态与机理。ADAMS［41］开发了一种二维有限元细观力学分析方法对金属基复合材料增强相与基体相间的结合进行分析（图8），认为应力及位移是在界面层上连续传递的，即认为界面层对于复合材料的力学性能影响较小。但实际上，无论是增强相与基体相间应力传递还是微观结构与性质，都不能简单地将界面相忽略。

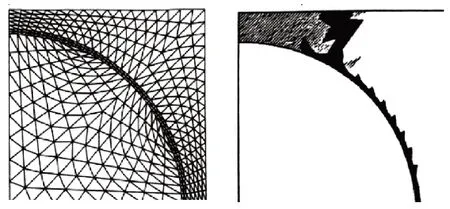
图8 复合材料界面相有限元模型及失效图［41］Fig.8 Finite element model and failure diagram of composite interface phase［41］

D.P.MONDAL 等［42］采用有限元法对金属基复合材料的界面进行了模拟，引入“界面有效系数”（η），并将界面相模拟成一层极薄的人工材料，通过改变人工材料的厚度与模量对其变形行为与界面刚度、界面厚度及增强相体积分数等界面特性的关系进行了研究，发现当界面有效系数小于2.0 时，复合材料劣化显著，当其小于0.8 时，则可认为材料失去了增强相的优势。MENG 等［9］通过建立碳化硅颗粒增强铝基复合材料细观力学模型（图9），对其界面强度和破坏机理进行了预测，当界面强度大于600 MPa时界面脱粘发生在塑性变形范围内；界面强度小于600 MPa界面脱粘发生在弹性变形范围内，且随着界面强度的增加，复合材料发生界面脱粘时的塑性应变呈上升趋势。界面强度和断裂能是颗粒增强金属基复合材料界面脱粘的关键因素。

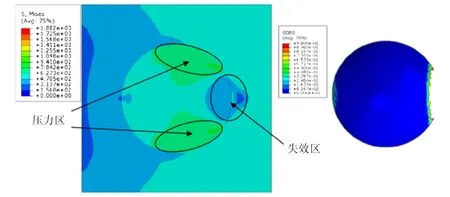
图9 金属基复合材料界面失效［9］Fig.9 Interface failure of metal matrix composites［9］

ZHANG 等［43］针对颗粒增强金属基复合材料，基于嵌入单元模型及有限元法研究了界面相对其的强化行为的影响（图10），发现颗粒增强相与基体相之间的硬界面相加大了颗粒对基体相的增强作用，较软的界面使基体出现孔洞，恶化了增强相的增强作用，另外，对于硬界面相，界面相与基体相的脱粘比界面相与颗粒增强相之间的脱粘对金属基复合材料的整体强化效果影响更明显。

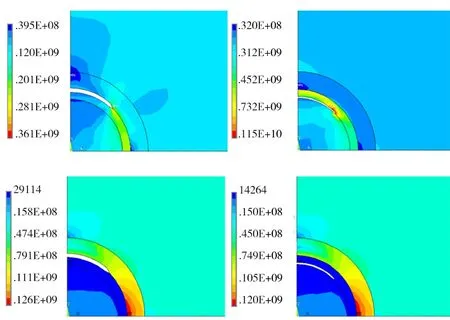
图10 金属基复合材料界面脱粘及应力分布［43］Fig.10 Interfacial debonding and stress distribution of metal matrix composites［43］

QING 等［44］基于对含界面相的SiC 颗粒增强金属基复合材料的变形和损伤演化的二维有限元模拟，同时对SiC 颗粒增强金属基复合材料进行计算实验，对界面相对金属基复合材料弹性及强度造成的影响进行了分析，发现界面相对材料弹性性能影响较小，而对其强度性能影响较大。孙继华等［45］针对金属基复合材料，仿真分析了金属基复合材料界面不同结合情况下的超声检测信号，获得了界面不同情况下的频谱特性差别。杨慧等［46］通过引入双夹杂模型，对含脆性界面相的颗粒增强金属基复合材料弹塑性损伤变形行为的颗粒尺寸效应进行了研究，发现在脱粘损伤时候，颗粒应力下降为零，使基体相与界面相的应力也相应降低。目前已通过有限元仿真方法对金属基复合材料界面层进行的分析中，对界面层对材料力学性能及失效脱粘的破坏机理的研究提供了理论依据，但仍存在不足，包括：目前机理分析多基于二维有限元仿真，因计算量较大和收敛困难等原因对更符合实际的三维有限元仿真研究较少；分析过程中单因素或单一参数影响分析较多，与实际工况类似的多因素综合影响分析较少。

4.2 内聚力模拟仿真

基于多种内聚力模型，金属基复合材料界面在力学性能及有限元模拟仿真等方面已取得阶段性研究成果。姜卓群［47］通过对结合最大应力失效准则的增强相、基体相及界面相失效模式的分析，获取了封闭的金属基复合材料的细观力学失效包线。但由于其在分析过程中忽略了纵向拉伸、压缩及剪切载荷下的应力集中效应，导致金属基复合材料强度预测精度偏低。刘昌明［48］基于双线性内聚力模型，使用有限元仿真软件对复合材料的细观结构等效基体相，增强相以及界面相对复合材料单胞模型进行了建立，对界面相出现初始损伤到裂纹完全扩展及界面脱粘的全过程进行了模拟仿真，结果符合基于内聚力模型复合材料界面脱粘的三个典型阶段：线弹性承载阶段、界面损伤阶段、界面损伤演化阶段（见图11）。当载荷较小时，界面结合完好，界面相在增强相与基体相间起传递应力的作用；当载荷达到界面的最大应力时，界面开始出现初始损伤，此时若继续增大载荷，则使界面承载能力迅速下降，进入损伤扩展阶段直至界面应力为零，界面完全脱粘失效。

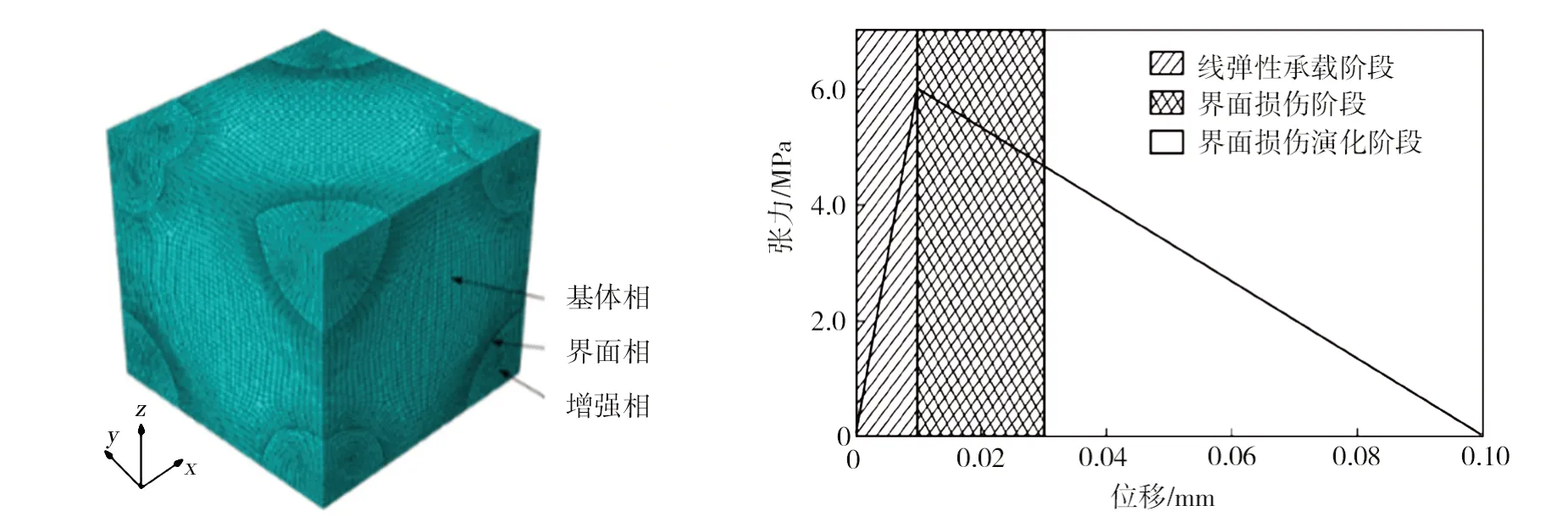
图11 复合材料模型［9］及界面处张力-位移曲线［48］Fig.11 Composite material model［9］and tension-displacement curve at interface［48］

刘敏等［49］基于UEL 用户子程序实现了Abaqus仿真平台上的内聚力界面二维二次单元的力学模拟，通过数值算例验证了该程序的准确性和有效性。其虽然在一定程度上能为开发其他类型的内聚力界面有限单元提供研究思路，但仍停留在二维层面。赵帅［50］基于卡尔曼滤波算法开发了一种用于表征内聚力模型参数的反演辨识算法，提出了更为真实的细观尺度的建模方法，实现了对复合材料力学性能和相关失效机理的研究，并利用计算均匀化的方法实现了界面脱粘的双尺度分析计算（图12）。但其提出的细观模型构建方法多基于二维，对于更为真实的三维模型还尚未进行深入研究，且只对沿固定路径的界面脱粘问题进行了研究，对任意路径的双尺度损伤与失效问题研究较少。

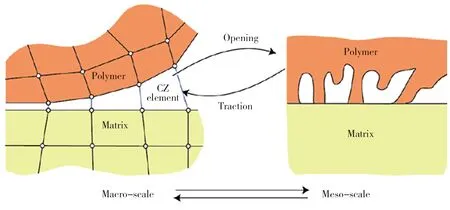
图12 界面双尺度方法［50］Fig.12 Two-scale method of interface［50］

张洪峰［51］基于多种内聚力单元，总结了内聚力单元的参数选择方法用来改善计算中遇到的数值问题，并通过双悬臂梁试验在不同参数下的算例验证了不同参数设置下对计算结果的影响，发现通过合理的内聚力单元参数设置可以使有限元仿真模型在较粗的网格下获得更为良好的效果，精度和效率均有所提升。周艳光等［52］针对Cu/SiC 金属基复合材料，进行了其在拉伸和剪切作用下的大规模分子动力学模拟，并通过建立原子级内聚力界面模型将其应用于有限元模拟，发现温度与界面结合强度是导致界面破坏发生脆-韧转换的关键因素。目前研究证明低温对金属基复合材料加工有积极影响［53］，但低温对材料界面相的影响仍不明确，该工作为研究低温对界面裂纹产生造成影响及研究金属基复合材料基体相与增强相塑脆转化提供了思路。

5 结语

本文对金属基复合材料界面层及断裂力学理论和内聚力模型进行系统综述和总结，梳理了可以较好地对金属基复合材料的界面行为进行表征的内聚力模型及其研究进展，并总结了目前应用内聚力模型对金属基复合材料的模拟仿真应用，目前研究仍存在以下问题：

（1）对于金属基复合材料界面相，细观模型多基于二维有限元模拟仿真，对于三维内聚力界面研究较少；

（2）金属基复合材料界面层的内聚力模型参数目前仅能通过有限元反演分析的方法来提高模型参数的准确性，仍难以通过直接实验的方式进行精准获取；

（3）目前针对内聚力模型在金属基复合材料界面相的研究多基于常温环境，对低温环境下的情况研究较少。

结合目前的研究现状，金属基复合材料界面相断裂损伤研究仍不完善，限制了其应用发展。进一步完善内聚力模型将其应用于金属基复合材料界面，以实现材料界面相断裂机理研究是今后研究的热点与方向之一。