带通滤波电路故障的BP网络诊断方法与仿真设计
王 恒,唐孝国,郭俊亮
(铜仁职业技术学院 信息工程学院,贵州 铜仁 554300)
0 引 言
随着各种智能化诊断方法的出现,模拟电路的故障诊断技术也得到了很大的发展。神经网络作为智能信息处理工具,已成为科学研究中最活跃和应用最广的学科之一。由于其可以克服小样本、高维数以及时变性等困难的优势,因此得到迅速的发展和广泛应用。目前神经网络主要用于线性或非线性模型的建模与仿真,而对于复杂网络研究还不够深入。与传统的故障诊断方法相比,人工神经网络不需要建立对象的精确数学模型,具有并行处理、联想记忆、自组织、自学习和较强的强非线性映射能力,同时又有很高的容错性能,能够对输入数据进行自动分类。由于神经网络可以克服小波变换存在“维数灾”问题,因此在故障诊断中具有巨大的潜力和应用前景,在实践中越来越受到重视。目前,模糊神经网络技术为故障诊断开辟了新的研发方向,模糊神经网络在本质上是双重模拟人脑的结构和思维功能,其可以充分利用各自的模糊理论和神经网络的优势,弥补其不足。此外,小波分析和神经网络的结合也是一个研究非常活跃的领域。传统的信号处理方法由于具有非平稳性、非线性和不确定性等特性,难以取得良好的效果,而神经网络可以以更高的效率和精度解决这些问题。另外,由于神经网络是由大量神经元构成的网络模型,因而能对复杂问题进行快速而准确地识别和判断,从而使之更易于推广到其他领域。因此,许多学者开始重视模拟电路故障诊断,并取得了许多成果。归纳起来,诊断方法大致分为6大类:故障字典法、故障参数识别法、验证法故障诊断、逼近法、人工智能法、神经网络法。
本文根据现有的研究成果,分析总结各种故障诊断方法的基本原理,运用基于BP神经网络的故障诊断方法,设计带通滤波电路的故障诊断方法,使用MATLAB软件进行仿真,使之能够有效诊断电路的故障。
1 BP网络模拟电路故障诊断方法概述
应用BP神经网络进行模拟电路故障诊断的方法一般是:在一定的测试激励下,将电路常见的各种故障状态及正常状态所对应的参数通过PSpice求出,进行数据预处理后作为BP网络的输入样本,对网络进行训练,然后在相同的激励下,检测电路实际输出,作为待诊断样本集提供给BP网络,网络输出即为对应的故障模式。
常用BP神经网络包括输入层、隐含层和输出层。其中,输入层没有神经元,只有信息输入;隐含层和输出层都可以相应地更改传入的数据。隐含层可以通过多次实验或经验公式得到,隐含层中每个神经元都有一个权值,其反映了神经元之间的联系程度,输入层和输出层的数量取决于输入向量和输出向量的尺寸。
采用BP神经网络进行故障诊断,需先建立故障字典,这一步需要设计电路的故障特征,对可能出现的故障进行归类,从而生成故障集,生成故障集能够消除故障诊断过程中大量的冗余信息和不精确信息。使BP神经网络能够对故障字典进行记忆,然后根据BP神经网络的模糊性和记忆性,获取测量数据集,按比例和随机方式收集数据,形成训练集和测试集。接下来对数据样本集进行预处理,因为很多样本数据是参差不齐的,直接训练会降低神经网络学习的效率。然后对电路状态进行记忆和推断,即输入新的状态参量时对电路状态进行推断,训练后将测试样本数据输入网络,获得预测结果。将预测结果与实际输出结果进行比较,验证网络性能是否满足设计要求,如果不能满足要求,则需要对网络的参数进行调整,甚至可能对网络结构进行调整,以便再次培训和学习,从而获得最合适的网络参数和网络结构。
2 带通滤波电路的BP网络故障诊断方法设计
2.1 带通滤波电路仿真设计
本文设计选用Sallen-Key带通滤波电路为主电路进行分析,电路具体参数为:1 kΩ、3 kΩ、2 kΩ、4 kΩ、4 kΩ、5 nF、5 nF,激励信号为5 V的交流信号。使用的仿真软件为OrCAD/PSPice,在OrCAD中绘制电路(如图1)。对电路进行交流分析(AC Sweep),考虑到元件中存在容差值,设定电阻的容差为10%、电容的容差为5%、激励信号为5 V、起始频率为1 kHz、终止频率为1 MHz的交流扫频信号。电路幅频响应波形如图2所示。

图1 Sallen-Key带通滤波电路Fig.1 Sallen-Key band pass filter circuit

图2 Sallen-Key带通滤波电路幅频响应波形图Fig.2 Sallen-Key band-pass filter circuit amplitude-frequency response waveform diagram
2.2 带通滤波电路灵敏度分析及故障测试点选取
利用PSPice的灵敏度分析仪对电路进行灵敏度分析,选用带通滤波电路的输出电压V(OUT)作为电路性能参数,根据电路元件的相对灵敏度,选择电路测试点。在PSPice软件中,可以利用MATLAB语言编程,计算出各种不同情况下的电路系统参数,对所得到的组件的相对灵敏度的分析结果如图3所示。

图3 Sallen-Key带通滤波电路相对灵敏度分析图Fig.3 Sallen-Key band-pass filter circuit relative sensitivity analysis diagram
通过相对灵敏度测试结果可知,2、3、1、2的相对灵敏度较大,因此测试点的选取应靠近这几个元件。根据所需数据的复杂性,并综合考虑计算和时间因素,选择1、2、OUT 3个测试点,作为故障数据的提取点(见图4)。

图4 测试点选取Fig.4 Test point selection
2.3 带通滤波电路的故障类型
根据图3中的灵敏度分析,当2、3、1和2发生改变时,能够对电路输出产生比较明显的影响。考虑软故障情况下2、3、1和2各组件状态,设置其高于或低于标称值50%时为故障状态,用“↑”表示偏大,用“↓”表示偏小。从而可以得到9种状态类型,分别是:无故障、2↑50、2↓50、3↑50、3↓50、1↑50、1↓50、2↑50、2↓50。通过设置故障类型输出值来区分网络识别结果,故障分类见表1。

表1 故障类型Tab.1 Fault type
2.4 原始数据采集及归一化处理
本文采用多测试点、多信息特征量的模拟电路故障诊断方法,即通过多个测试点提取不同频率信号下的电压值做为原始训练数据。运用OrCAD进行电路仿真,在软件绘制中如图4所示电路,输为5 V、1 kHz、1 MHz的交流扫频信号,进行交流分析(AC Sweep),输出频响曲线如图5所示。3条曲线分别为OUT、1、2,3点的输出频响曲线,褐色曲线“□”表示OUT的输出频响曲线,绿色曲线“◇”表示1点的输出频响曲线,红色曲线“▽”表示2点的输出频响曲线.

图5 输出频响曲线Fig.5 Output frequency response curve
根据其它8种故障状态,直接修改相应元件的数值,重复进行交流分析,得到图6中(a)、(b)、(c)、(d)的输出频响曲线。

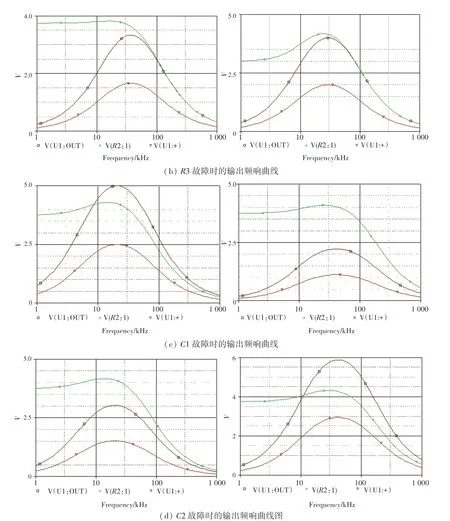
图6 R2、R3、C1、C2故障时的输出频响曲线Fig.6 The output frequency response curve when R2、R3、C1、C2 fails
通过仿真波形可以看到,当元件发生故障时,3条波形变化最大的区域在3 kHz~30 kHz的范围内,3个测试点的电压对每种状态的情况具有代表性。因此,为了尽可能少截取到对训练无用的数据,选择在3 kHz~30 kHz频率中截取训练数据。
仿真分析时,将交流分析的起始频率和终止频率分别设定为3 kHz和30 kHz,对以上9种状态各自进行20次蒙特卡洛实验,每次蒙特卡洛分析得到3个输出点各20条曲线,如图7所示。

图7 电路无故障时蒙特卡洛分析仿真图Fig.7 Monte Carlo analysis simulation diagram without circuit failure
设定每单位采样点数为40,则从每条输出频响曲线上能提取41个不同频点对应电压值,每种状态下提取20组3×41维的数据序列,9种状态下共能获得9×20组123维的原始数据样本,将其作为训练样本集。节选其中每种情况下各两组3 kHz和30 kHz频率下的输出电压值,见表2。
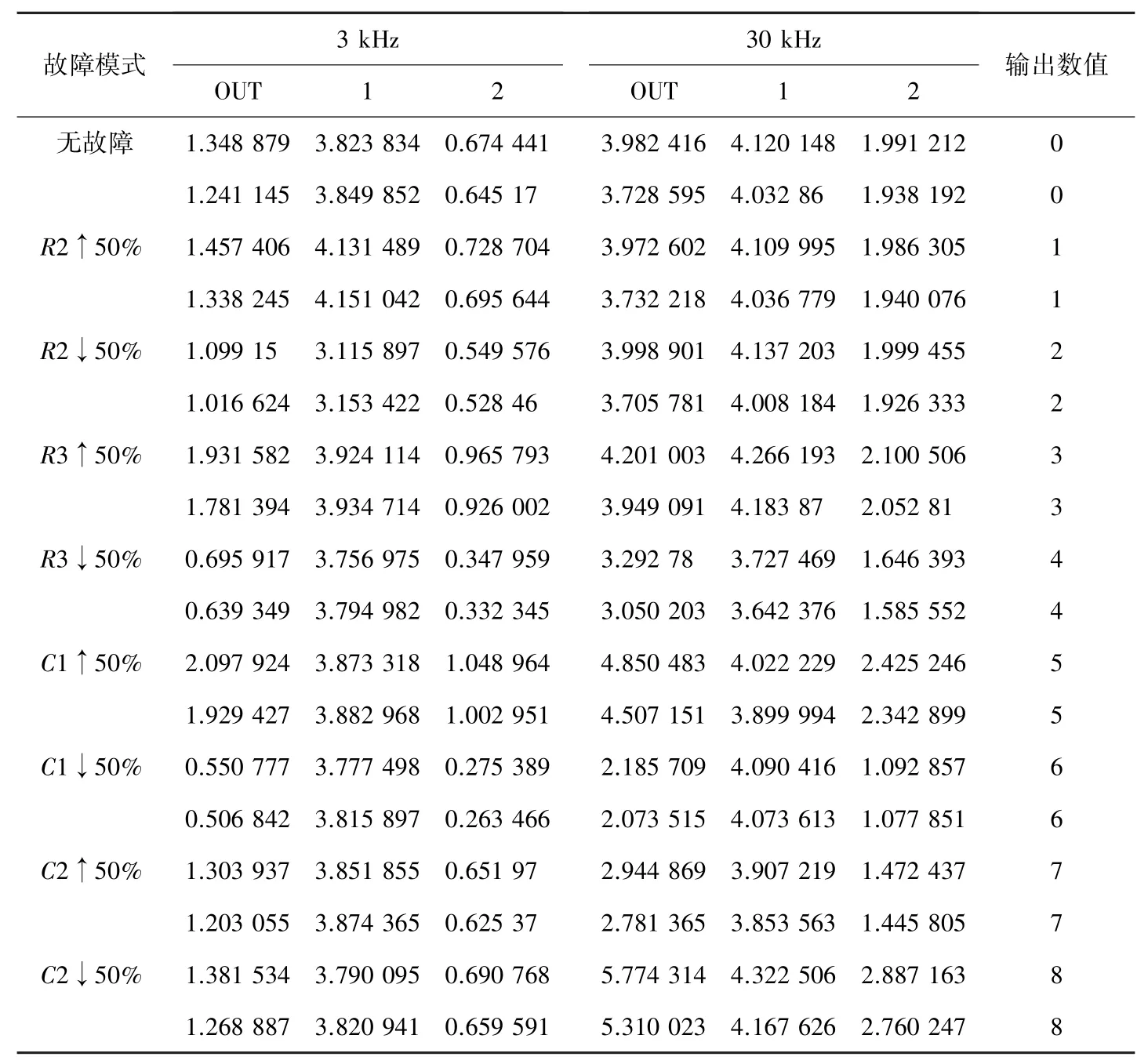
表2 原始训练数据节选Tab.2 Examples of the original training data
2.5 BP神经网络故障诊断网络结构设计
设计BP网络时,主要利用MATLAB神经网络工具箱完成网络的构建。
(1)确定网络的结构。输入输出层节点的数量由输入输出训练样本的数量确定,每个采集的样本集包含123个数据集和1个输出集。
(2)隐含层设计。一般情况下,单个隐含层满足大多数应用场景。虽然多层隐含层可以进一步减少误差,但其使网络变得复杂,增加了训练时间。为了减小误码率和计算量,可采用多个隐含层同时进行数据融合处理。
通过反复试验确定了123-10-1的网络结构;为了使神经网络能适应复杂系统,可将其分为3层结构:输入层、隐含层及输出层。其中前两层为简单模型,后一层为精确模型。
3 带通滤波电路故障诊断MATLAB仿真
3.1 BP神经网络MATLAB仿真设计
在进行BP网络设计时,采用MATLAB神经网络工具箱对网络进行构造和初始化。在此基础上,为了验证该方法的有效性,原始数据中有180套数据,其中150套是随机抽取的训练集,30套是测试集。通过仿真得到了BP网络训练的训练效果。以下为MATLAB程序设计的主要部分:
(1)导入数据。180组输入数据集y和输出数据集x分别放在61.mat和6.mat文件中,首先导入数据集x和y。

(2)产生1~180的随机数排列的数组。用以随机提取测试集和故障集。

(3)定义数据。定义输入集为input,输出集为group。
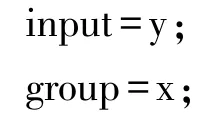
(4)提取150组为训练集,提取30组为测试集。

(5)数据的归一化预处理。

(6)初始化网络结构。

(7)网络训练。

(8)预测输出。将测试集连接到经过训练的网络得出诊断数据,并让数据进行反归一化处理。

3.2 实验数据与结果分析
运行程序后,诊断结果准确率如图8所示。其中,预测类别是BP网络诊断结果,输出类别是实际故障类型。经多次重复运行程序,诊断结果准确率均在90%以上,说明本文设计的BP网络诊断故障成功率较高,可以有效的进行故障诊断。实验结果表明,神经网络对故障诊断具有一定的效果,预测和输出类别完全相同,误差的减少如图9所示。

图8 预测与实际结果对比图Fig.8 Comparison between prediction and actual results

图9 BP网络结构仿真误差曲线图Fig.9 BP network simulation error curve
通过仿真结果及过程可以看出,本文设计的BP网络结构模型能快速训练将误差缩小到目标值,预测结果准确率高。说明BP网络的收敛速度较快,故障的定位准确率较高,确实是故障诊断中一种较优越的选择方案。
4 结束语
本文基于神经网络原理,通过对带通滤波电路的故障诊断方法设计,分析了模拟电路故障诊断的方法。在故障提取中,采用多测试点、多信息特征的方法,使故障集数据更具有代表性,并对网络进行更好的训练。利用MATLAB软件建立了BP神经网络的故障诊断模型,并对BP网络进行了训练,得到了仿真结果。利用该诊断模型对一个实际的模拟电路进行故障诊断。仿真结果表明,BP神经网络能够较快地达到目标误差,具有较高的诊断识别率,从而证明神经网络在模拟电路故障诊断中具有良好的应用效果。

