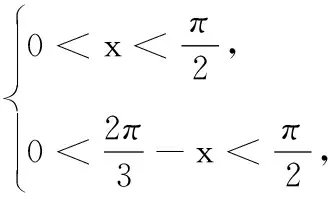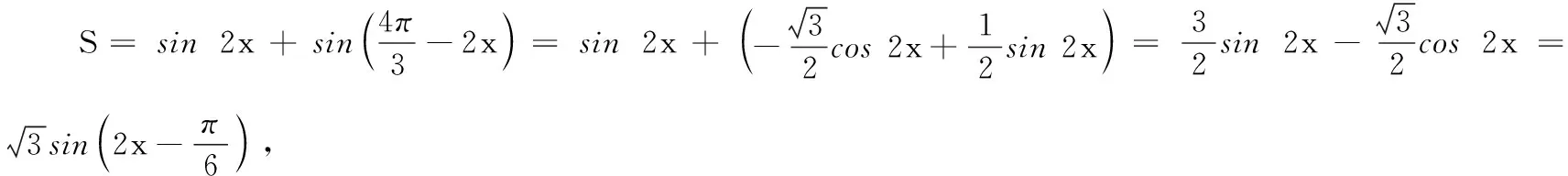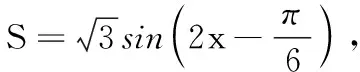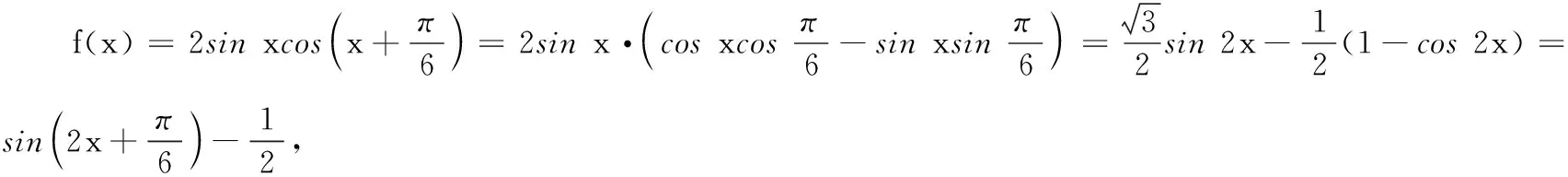高一数学测试

一、单项选择题(本大题共8小题，每小题5分，计40分)

1.tan 255°等于( )

2.sin 22°sin 52°+sin 68°sin 38°等于( )

4.在∆ABC中,a,b,c是角A,B,C分别所对的边,若A∶B∶C=1∶2∶3,则a∶b∶c=( )

(A)1∶2∶3 (B)3∶2∶1

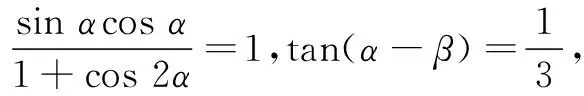
(A) 1 (B)-1 (C) 7 (D)-7

8.a,b,c是∆ABC中角A,B,C分别所对的边,根据下列条件解三角形,有两解的是( )

(A)a=1,b=2,A=30°

(B)a=30,b=25,A=130°

(C)a=6,b=9,A=45°

(D)a=9,b=10,A=60°

二、多项选择题(本题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)

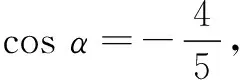
10.在复平面内,下列说法正确的是( )

(B)若复数z满足z2∈R,则z∈R

(C)若复数z=a+bi(a,b∈R),则z为纯虚数的充要条件是a=0

(D)若复数z满足|z|=1,则复数z对应点的集合是以原点O为圆心,以1为半径的圆

11.定义平面向量之间的一种运算“⊙”如下:对任意的向量a=(x1,y1),向量b=(x2,y2),令a⊙b=x1y2-x2y1,则下列说法正确的是( )

(A)若a与b共线,则a⊙b=0

(B)a⊙b=b⊙a

(C)对任意的λ∈R,有(λa)⊙b=λ(a⊙b)

(D)(a⊙b)2+(a·b)2=|a|2|b|2

12.在∆ABC中,a,b,c是角A,B,C分别所对的边,下列命题正确的为( )

(A)若sinA>sinB,则A>B

(C)若acosA=bcosB,则∆ABC为等腰三角形

三、填空题(本大题共有4小题,每小题5分,计20分)

13.已知向量a=(2,3),b=(-1,2),则|a-2b|=______.

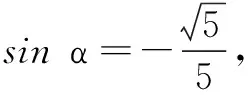
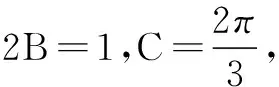
四、解答题(本大题共6小题,计70分.解答应写出文字说明、证明过程或演算步骤)

17.(本小题满分10分)复数z1=a+4i,z2=-3+bi,若它们的和z1+z2为实数,差z1-z2为纯虚数,求实数a,b的值.

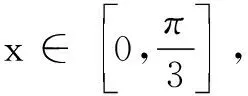
(1)若m∥n,求x的值;

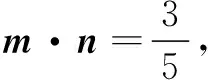
(1)求A;

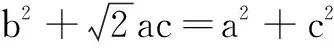
(1)求f(x)的最小值,并写出f(x)取最小值时x的取值集合;

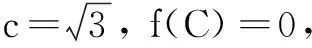
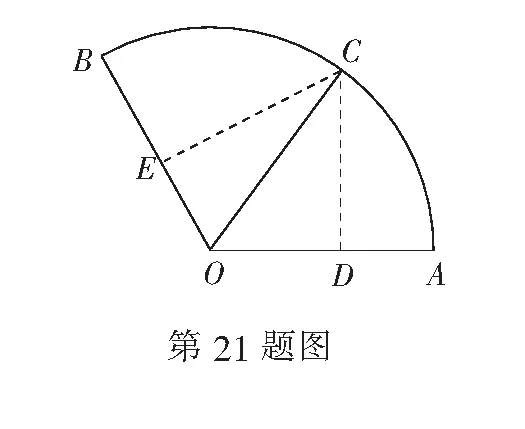
(1)设∠COD=x,将四边形CDOE的面积S表示成x的函数并写出定义域;

(2)求四边形CDOE的面积S的最大值.

参考答案

一、单项选择题

1.D;2.D;3.C;4.C;5.B;

6.A;7.B;8.D.

二、多项选择题

9.CD;10.AD;11.ACD;12.ABD.

三、填空题

四、解答题

17.因为z1+z2=(a-3)+(4+b)i为实数,所以4+b=0,b=-4.

又因为z1-z2=(a+3)+(4-b)i为纯虚数,所以a+3=0且4-b≠0,得a=-3且b≠4.综上,a=-3,b=-4.

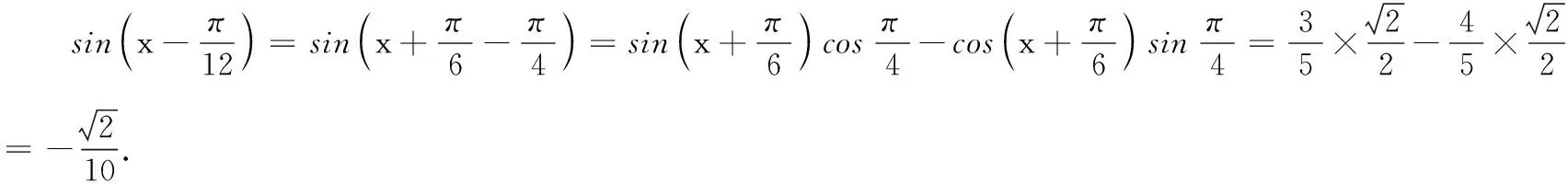
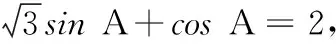
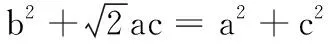
(选择① 或② 的结果相同)

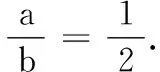
要得到题设中的四边形CDOE,必须