融合双重策略粒子群算法的分布式电源配网无功优化

李子健，郭佩乾，马宁宁，吴爱军，杨敏珑

(1. 国网上海市电力公司市区供电公司，上海 200080；2. 电力系统及大型发电设备安全控制和仿真国家重点实验室(清华大学电机系)，北京100084)

0 引言

为积极响应国家提出的“双碳”目标与十四五电力规划要求，需大力发展可再生能源，加快能源低碳转型，实现以新能源为主体的新型电力系统。在此背景下，积极优化各类型能源配置，大力推进以光伏和风电为主的分布式可再生能源的建设成为重要研究方向[1 - 2]。

与此同时，传统配电网系统逐渐朝着智能化方向发展。为保障配网系统高效的自动化管理和稳定经济的运行，及时准确地实现潮流分析和优化是基本前提[3]。然而，可再生能源在高密度、大规模的接入的同时，分布式发电技术驱使原有配电网结构更加复杂多变[4 - 5]。此外，可再生能源本身特点也对现有配网的潮流方向、电压分布和网络损耗等产生巨大的影响[6]。如何在保证新型配电网系统稳定和经济运行的前提下，实现大规模分布式可再生能源的接入成为亟待解决的问题。

针对交流配电系统的网络损耗和电压质量优化已有一定研究基础[7]。通过增设无功补偿装置(static var compensator, SVC)接入配电系统，调节接入点无功功率和无功特性，能有效提升功率因数，是实现降低网络损耗且稳定高效的方案之一[8]。配电网无功优化是在系统运行在约束条件时，通过调整系统内无功设备出力，在维持系统电压稳定的前提下，使网损功率达到最小值的有效方案[9]。为解决以上多目标综合最优化问题，研究人员将遗传算法、粒子群算法和神经网络算法等各类优化方法应用于配网无功优化[10]。文献[11]结合秩相关系数联系风速与负荷，通过混合整数二阶锥模型进行多场景无功优化。文献[12]则针对“光-储”联合的增量配网系统，依靠光伏逆变器和储能对无功与有功功率调节能力，构建了时段解耦的动态无功优化模型。通过灾变遗传算法，实现增量配网动态无功优化，实现节能减损。同样地，文献[13]在考虑电压越限的风险的基础上，通过时间解耦并将灾变遗传算法应用在无功补偿和电压控制领域，实现长时间尺度下的系统无功优化调度。文献[14]提出基于二阶段鲁棒优化模型的无功电压控制策略，在考虑可再生分布式电源出力预测误差以及存在误差较大情况下，以最小成本实现系统电压无功控制，提高了配网运行的经济性。上述方案虽在配网无功优化问题上取得较好效果，但在稳定性与适应性上仍有优化空间。粒子群优化(particle swarm optimization，PSO)算法[15]以其收敛速度快、计算结构简单等优势也可应用于配网系统的无功优化配置领域。然而在应用于目标对象复杂情况时，传统PSO算法存在收敛过早或优化速度缓慢的问题。针对该缺陷，诸多改进式PSO方案被提出，以平衡该算法在的全局搜索与局部搜索能力[16]。文献[17]引入自适应惯性系数结合变异算子进行优化，使得粒子搜索行为脱离局部“陷阱”。文献[18]结合模糊逻辑控制与PSO算法，提升了群体的多样性，加快收敛速度。文献[19]提出基于时变加速系数的自适应粒子群算法，提升算法全局搜索能力。但上述研究仅为改进PSO算法单方面特性进行优化，未全局考虑算法收敛速度慢、易陷入局部搜索困局等问题。

基于以上，本文首先对含分布式可再生能源的配网优化目标、约束方程、控制变量以及标准粒子群算法展开了分析。然后结合上述研究结论，提出了一种融合天牛须算法与粒子群算法的双向学习优化算法，将衡量交流配电网的有功损耗及电压质量作为目标函数，以交流配电网运行边界作为约束条件，建立多目标优化模型，应用于含分布式可再生能源和静止无功补偿设备的配电网无功优化。最后，基于IEEE 33节点的增强分布式能源配电系统模型，对本文所提融合天牛须搜索的双向学习粒子群优化算法进行了有效性和优越性的验证。

1 含分布式可再生能源的配网系统无功优化模型与标准粒子群优化算法

1.1 含分布式可再生能源的无功优化模型

针对分布式发电电源(distributed generation，DG)接入的配电网，通过控制系统无功功率，对系统有功网损进行控制的同时优化系统节点电压。其数学模型包括目标函数、功率约束和控制变量方程。

1.1.1 分布式可再生能源并网模型

参考已有可再生能源并网等效计算方案，本文将所增设的分布式可再生能源接入方式分为3类。

1)分布式可再生能源PQ接入方式

对于双馈型风机与SVC等恒功率因数运行的分布式可再生能源，本文将其视作PQ节点。在开展系统潮流计算时，通常将其认作输出为负功率的负荷，潮流计算等效模型可表示为：

(1)

式中：P与Q为电源模型等效为负荷的有功功率与无功功率；Pws和Qs分别为双馈型风机与SVC等恒功率因数运行的分布式可再生能源输出的额定有功功率和无功功率。

2)分布式可再生能源PV接入方式

对于异步风力发电机组类型通过逆变装置并网的分布式能源，本文视作PV节点处理，其潮流计算所需的等效模型详见文献[20]方法。

3)分布式可再生能源PI接入方式

对于光伏电站类型采用直流电流控制逆变器接入的分布式可再生能源，可将其等效为PI节点。此类节点在潮流计算时可开展如下处理：

(2)

式中：t为迭代次数，Qsolar(t)为光伏电站类型分布式可再生能源第t次迭代的无功功率；Psolar为光伏电站有功功率；Isolar为向配电网注入电流幅值；Usolar(t-1)为第(t-1)次迭代计算所得节点电压值。随后，通过以上公式可得该PI节点转化PQ节点函数。

(3)

1.1.2 系统优化目标函数

有功网损是配电网中重要的经济与技术指标，从提升经济性考虑应对设备运行状态应进行优化。同时节点电压偏差作为影响用电设备效率与工作状态的重要指标，也需一并考虑。

本文建立以含分布式可再生能源配电网系统有功损耗及节点电压偏差为控制目标的目标函数，其控制目标优先考虑系统有功网损的最优化，兼顾电压偏差量控制，其表述为：

minF=min{(1-λ1)F1+(1-λ2)ηF2}

(4)

(5)

(6)

λ1+λ2=1

(7)

式中：F1为有功网损控制目标函数；F2为电压偏差量控制目标函数；n为总网络支路；Pg为有功功率总输入；PDG,i为各节点分布式电源有功功率输入；PL为配电网各有功负荷；ΔVi为节点电压越限偏差量；Vimax与Vimin分别为该节点允许的最大和最小电压值；λ1与λ2分别为目标函数权重系数，可根据控制目标偏重调整。

当ΔVi≥Vimax时，ΔVi=ΔVi-Vimax；当ΔVi≤Vimin时，ΔVi=Vimin-ΔVi；当Vimin≤ΔVi≤Vimax时，ΔVi=0。本文取λ1=0.7，λ2=0.3；η为控制电压偏差量的罚系数，根据文献[21]提出的震荡发散罚系数处理方法，其表达为：

(8)

式中：k1为约束引力递增系数；t为迭代次数；T′为震荡发散周期长度；k2为引力递减系数，其设计有利于保障收敛。本文中k1=0.2，k2=0.02，T′=300。

1.1.3 功率约束方程

对于该无功优化模型，各节点须满足有功功率与无功平衡，即满足式(9)的条件。

(9)

式中：Pi和Qi为节点i发电机的有功和无功出力；PGi与QGi分别为节点i注入的DG有功与无功出力；PLi与QLi分别为节点i的有功功率与无功功率负荷；QiSVC为i节点连接的静止无功补偿装置SVC的无功出力；θij为节点i、j之间的电压相角差；Gij和Bij分别为节点的电导和电纳。

1.2.4 模型变量约束

在实际模型中，各节点电压和无功补偿容量限定在一定范围内，以确保电能质量和投资控制。配网接入DG后，通过静止无功补偿设备SVC的接入控制节点电压幅值，变量约束条件如式(10)所示。

(10)

式中：PGi和QGi分别为含分布式可再生能源DG系统的有功和无功功率出力值；PGimax、PGimin分别为含分布式可再生能源DG系统的有功功率出力上限设定值和下限设定值；QGimax、QGimin分别为含分布式可再生能源DG系统的无功功率出力上限设定值和下限设定值；Uimax、Uimin分别为节点电压的上限和下限设定值；QiSVCmin、QiSVCmax分别为i节点连接的为静止无功补偿装置的允许出力最小值与最大值。

1.2 标准粒子群算法

根据标准粒子群算法[15]，其搜索更新公式为：

(11)

xi(t+1)=vi(t)+xi(t)

(12)

本文在第2节将提出一种改进粒子群算法，并对其在含可再生能源分布式接入配网系统的适应性开展分析和验证。

2 融合天牛须搜索吸引排斥和双向学习的改进粒子群算法

对1.2节分析可知，传统PSO算法采用的惯性权重与学习因子更新方式较为单一，易使搜索陷入过早收敛[22]。据此，本文基于文献[23]提出的一种双重自适应调整策略，结合全局寻优的天牛须智能算法，在搜索过程中自适应调整惯性权重与学习因子，平衡并增强算法的全局与个体搜索能力。

2.1 天牛须全局寻优算法

天牛须搜索(beetle antennae search, BAS)算法受天牛觅食启发的仿生算法[23]，模仿其触角双向探测比较的搜索方式，搜索方式以个体为单元，具有运算量少和收敛速度快的优势。

具体搜索过程可分为两个步骤：搜索行为和检测更新行为。该算法在迭代过程中会通过随机方向开展移动搜索，且每次需要先对搜索方向进行矢量归一化处理[24]。进而，矢量归一化处理方式可通过计算公式(13)获得：

(13)

式中：random函数表示一个随机函数；j为当前搜索位置的维度。

同时，用式(14)来建立天牛须全局寻优搜索的区域模型：

(14)

式中：xleft和xright分别是现在搜索位置维度的左侧搜索空间和右侧搜索空间；dt是天牛须到天牛质心之间的搜索区域范围。

进而，天牛须最优搜索根据当前位置维度，可按照式(15)进行更新搜索和移动：

x(t+1)=x(t)+δ(t)bsign(f(xright)-f(xleft))

(15)

式中：δ(t)为天牛须搜索算法搜索步长；f为用来计算对应函数适应度值。bsign用来规定搜索算法向当前维度左侧搜索范围或者右侧搜索范围的方向。

因此，对式(13)—(15)分析可知，天牛须搜索算法在进行一次迭代过程中只在单次搜索维度方向上开展一次探索。同时，每一次搜索迭代目标函数无论为何值，天牛所处的位置都进行更新。因此，固定步长会导致天牛陷入局部最优位置，无法实现全局寻优[25]。

2.2 惯性权重与学习因子更新

基于上述，所提改进的粒子群融合天牛须寻优计算所设定的惯性权重更新方式为：

(16)

式中：ωmin和ωmax分别为惯性权重的最大值和最小值，取值为0.1和0.8；A为曲线斜率参数，值为6；t为迭代数；T为迭代上限数。

对于学习因子c，采用单粒更新方式，结合自适应学习，其更新方式为：

(17)

式中：cmin和cmax分别为学习因子最小和最大值，取值为0.5和2；Ffit为t次迭代的粒子适应度；fmax为t次迭代后粒子适应度最大值。

采用该惯性变量和学习因子更新方式，可在搜索早期快速更新粒子速度，避免过早收敛。在搜索后期，惯性权重更新步进减缓，配合学习因子增长提升局部搜索能力，增强搜索精度。

2.3 双向学习与吸引-排斥策略

传统PSO算法基于选取较优值的单向更新方式，而本算法融合天牛须算法的双向搜索，将每次迭代的结果xi(t)与排序后的结果中随机较优结果xk(t)正反向比较，选取更优结果，其更新后公式如式(18)—(19)所示。

(18)

xi(t+1)=xi(t)+vi(t+1)

(19)

式中：ω为惯性权重；c为学习因子，根据式(16)—(17)随迭代进行更新。该更新方法扩大了粒子的学习范围，增强了全局搜索能力，减少了过早收敛的概率。

参考粒子位置更新方式，结合文献[26]提出的引斥力规则和双引力规则采用吸引-排斥策略，其更新方式为：

(20)

2.4 自适应决策因子

该算法中引入决策因子F，使算法在不同搜索阶段在双向学习策略和吸引-排斥策略中选择较优方式，兼顾算法搜索优势同时加快收敛速度，提升算法效率。决策因子F的表达方式为：

(21)

式中：d1=0.4；d2=0.6；a为决策因子曲线斜率参数，值为10；T为最大迭代数。

综合以上，所提出的融合天牛须搜索的改进粒子群算法计算流程如图1所示。

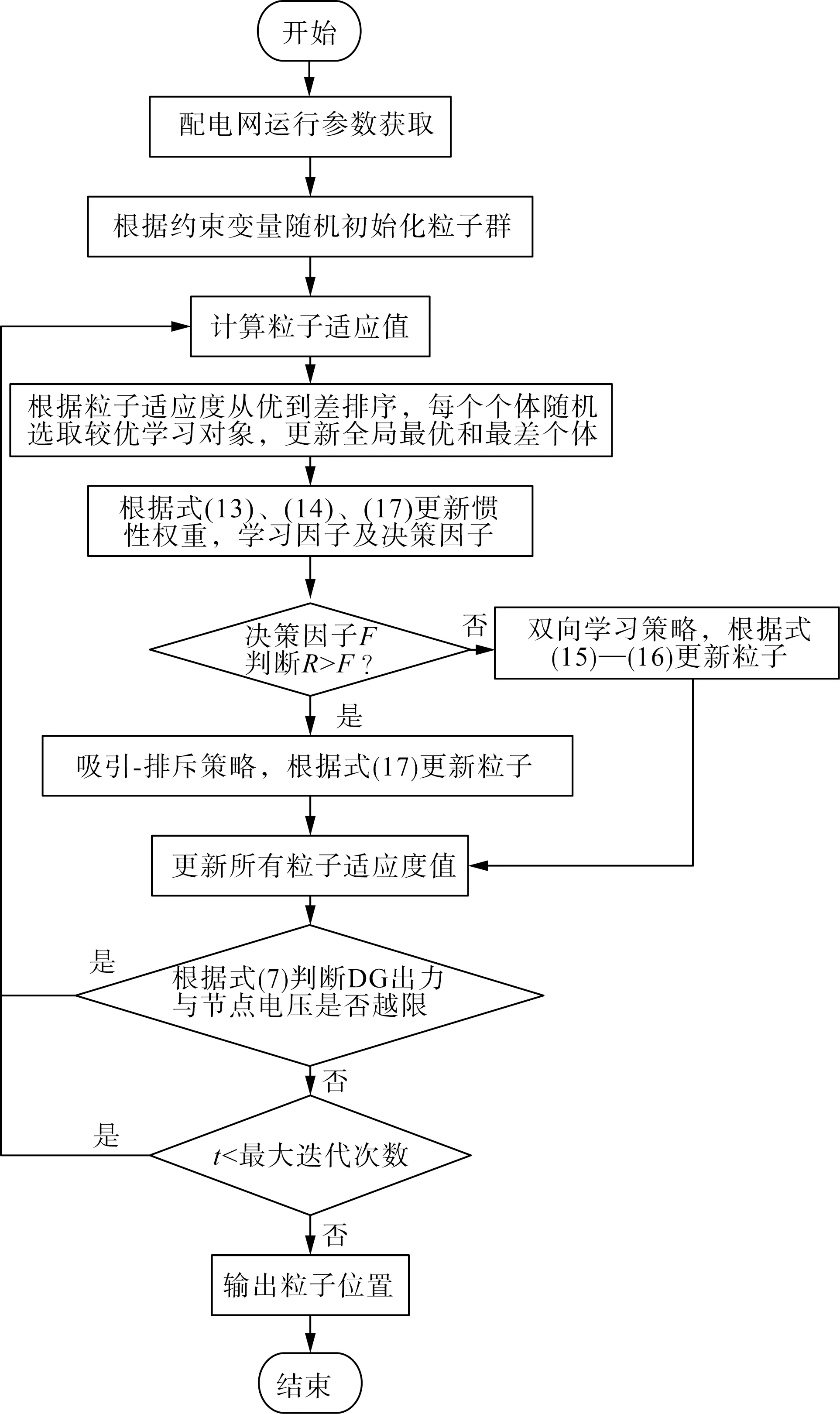
图1 改进PSO算法流程图Fig.1 Improved PSO algorithm diagram

3 算例分析

3.1 算例模型与算法参数设定

为验证本文所提改进粒子群算法在含多种分布式电源配电网系统应用中的优越性与可行性，本文基于Dolatabadi等提出的增强分布式发电的IEEE 33节点配网模型[27]开展了算例分析，结构如图2所示。(该配电网模型对于分布式电源接入配电网进行节点优化，更加符合配电网发展和研究方向。)

图2 增强分布式发电IEEE 33节点系统Fig.2 IEEE 33-node based distributed renewable system

标准IEEE 33节点模型如图2中无虚线部分，本文在节点18、22、25、33不同区域分别加入3种不同类型的分布式电源，节点18、33加装了无功补偿装置，容量设定为1 Mvar。进而本文DG主要并网参数如表1所示。

表1 分布式电源主要参数Tab.1 Main parameters of distributed generations coefficients

增强分布式发电的IEEE 33节点模型基准电压为12.66 kV，功率基准值为10 MVA，有功负荷曲线见图3所示。同时，本文中采用功率曲线时间轴均以15 min，即0.25 h为节点。节点18、33采用光伏分布式能源接入，节点22、25采用风电分布式能源接入，功率随时间变化的曲线如图4所示。

图3 IEEE 33节点系统有功负荷曲线Fig.3 Active power curve of IEEE 33-node system

图4 风电与光伏电源日内出力Fig.4 Typical daily power data of wind and solar energy

所提融合天牛须寻优与双重策略的改进PSO算法主要仿真参数设定如表2所示。

表2 改进PSO仿真参数设定Tab.2 Coefficients of improved PSO algorithm

3.2 仿真结果与对比分析

3.2.1 改进PSO算法效果分析

为了更好地反映所提改进粒子群算法在算例环境下收敛速度的优越性，本节首先对采用传统单向更新惯性变量PSO和所提改进PSO算法的仿真效果开展对比。以增强分布式电源IEEE 33节点模型为基础，经仿真验证，两种算法均可在20次迭代内实现收敛，收敛特性结果对比图如5所示。

同样地，根据图5中网损对比可知，未加任何无功优化控制方案的配网系统有功电量损耗可达2 618 kWh左右。系统分别投入所提无功优化控制方案与传统无功优化控制方案后，最大有功电量损耗分别为1 795 kWh左右和1 826 kWh左右。

图5 改进PSO与单向更新PSO算法收敛对比Fig.5 Convergence comparison between improved PSO algorithm and unidirectional updating PSO algorithm

对比无功优化控制投入后配网系统有功损耗可知，系统稳态后有功电量损耗减少量分别约为31.5%和30%，随着配网系统容量的增加，该有功电量损耗的减少量将十分可观。同时，根据收敛计算结果可知，本文采用改进PSO算法其收敛速度较传统PSO算法有较大优势，其收敛所需迭代次数降低率可达30%，对于改进优化速度有较大的促进。

图6为所提改进的PSO算法和传统惯性动量PSO算法的多方面对比结果。根据图中收敛迭代次数对比分析可知，对于本文所采用的IEEE 33节点系统，改进PSO算法收敛迭代所需次数仅为6，而传统PSO算法则需9次，迭代效率提升约1/3。同样地，随着配电系统容量的增加，对于更为复杂、多变的配网系统的网络结构，所提改进控制方案可有效提升迭代效率。

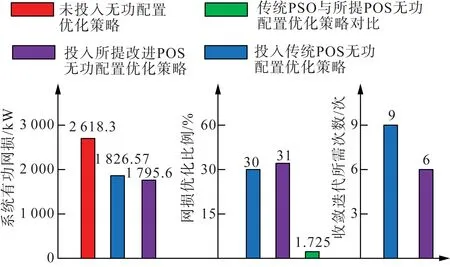
图6 改进PSO与单向更新PSO优化效果对比Fig.6 Optimization comparison between improved PSO algorithm and unidirectional updating PSO algorithm

据此，本文所提的改进PSO算法相较于传统PSO算法在配网系统网损优化计算中收敛速度和寻优能力上均有提升。

3.2.2 系统网损影响分析

依据上文算例的数学模型及算法应用，此处输出24 h内经改进PSO算法和传统算法优化的无功补偿设备接入的配网网损，并与无补偿设备投入的接入节点数据进行对比。有功网损对比结果如图7所示，投入无功优化后系统有功网损优化比例如图8所示。(注：将未投入无功设备进行优化的网络损耗减去改进PSO算法优化无功补偿设备接入的配电网网损所得的差值，除以未投入无功补偿设备接入的配网网损，所得的比值用百分比表示，即为图8所示有功损耗优化比例。)

根据图7中对比结果可知，在终端用户高峰用电期间，即早上7时左右与下午16时左右，未投入无功补偿设备和相应优化策略时配网网损最高可到150 kW和155 kW左右。随着改进PSO算法优化无功补偿设备的接入，系统有功损耗可减少至最大107 kW和110 kW左右。

根据图8中配网系统的有功网损优化比例可知，经过改进PSO算法完成无功补偿设备优化配置策略后，系统有功网损优化效率最大值可达42%左右，最小值约13%左右。结合以上对比结果可知，经改进PSO算法优化无功补偿接入对于配网系统的网损降低起到明显作用，优化后的静止无功补偿设备SVC接入使系统无功吸纳与支撑能力明显提升，增强了配电网功率传输能力。

图7 IEEE 33节点系统有功网损对比Fig.7 Active power loss comparison for IEEE 33-node system

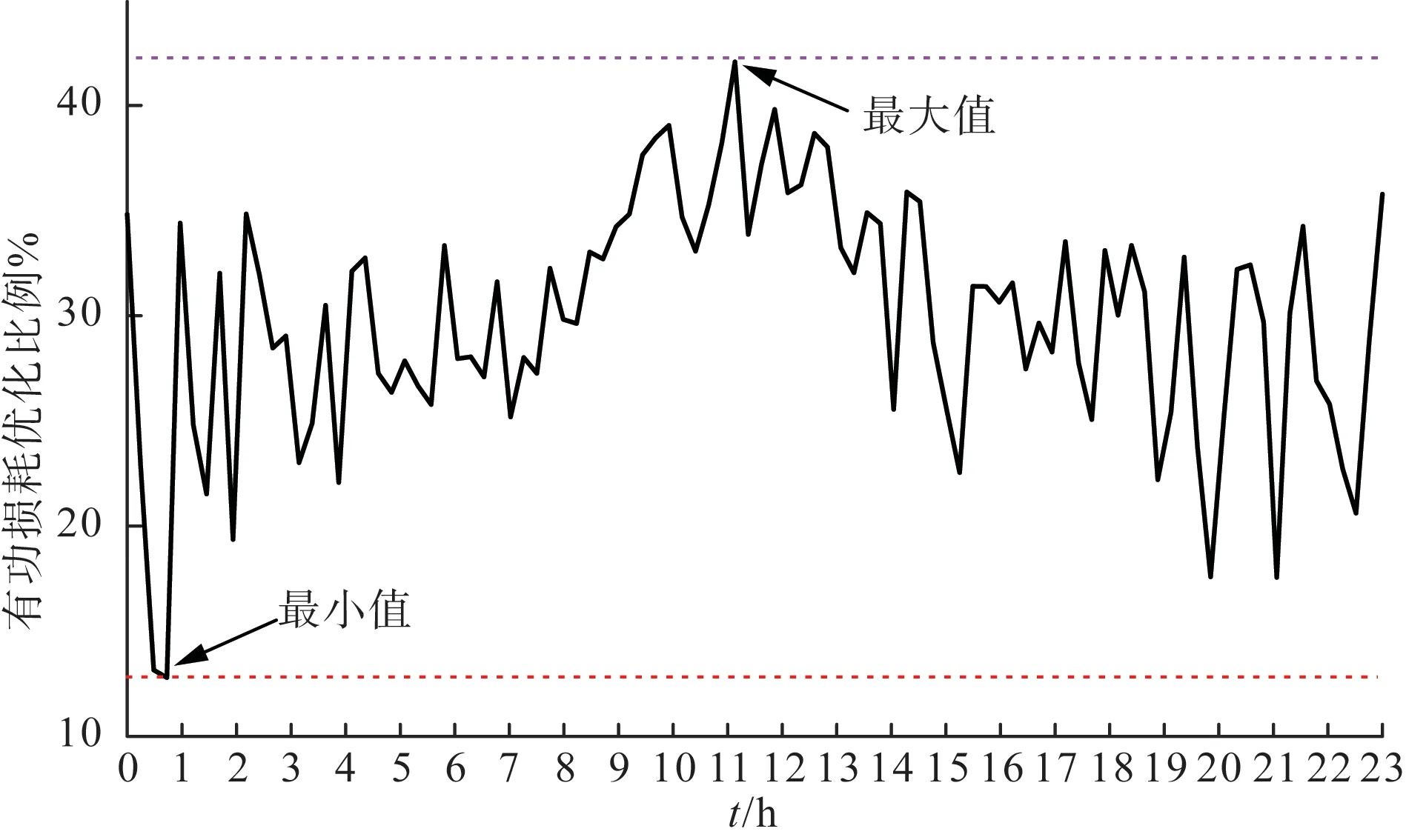
图8 IEEE 33节点系统有功网损优化比例Fig.8 Active power loss optimization ratio for IEEE 33-node system

3.2.3 系统节点电压影响分析

依据本文算例模型，选取全天最大负荷时节点电压值，分别输出接入经优化无功补偿设备和未接入无功补偿节点电压。据此，含分布式可再生能源接入和静止无功补偿设备的增强式IEEE 33节点电压变化对比结果如图9所示。

图9 IEEE 33节点电压变化曲线与比较Fig.9 Voltage comparison curve for IEEE 33-node system

根据图9可知，在配电网未加装无功优化策略时，系统电压最低达在32节点到0.937 p.u. 左右。对于传统PSO优化，其节点电压幅值最低出现在12节点处，为0.95 p.u.左右。随着所提改进无功优化策略的投入运行，节点电压幅值最低出现在30节点处，达到0.955 p.u.左右。而32节点电压也抬升至0.96 p.u. 左右。

此外，为研究本文所提优化策略的在33节点系统的普适性，节点16作为PQ节点，其功率需求具有一般代表性。选取其24 h电压值作为比较，计算结果如图10所示。在用电高峰期，未投入无功设备优化控制策略时系统最大电压跌落可达0.928 p.u.左右。经过改进PSO算法完成无功补偿设备优化配置策略后电压跌落有显著抬升，最低可达0.95 p.u.左右。相对传统PSO优化结果，本文所采用的PSO优化方式减少了节点电压的波动。

图10 算例节点16一日内电压变化比较Fig.10 Comparison of voltage changes for node 16 in case study

为更加直观地反映所提改进PSO无功补偿设备优化策略的效果，表3对16号节点一天内的电压比较和节点电压抬升率开展了详细对比。

因此，结合图9—10和表3可知，分布式可再生能源接入配网系统经无功补偿优化投入可明显优化各节点电压幅值，减少负荷和分布式电源输入变化对配电网节点电压的影响，将电压幅值限定在0.95～1.0 p.u.的合理范围，并减少电压波动，有效提升电能质量。

表3 节点16一日内电压比较Tab.3 Comparison of daily voltage changes for node 16

4 结语

本文以降低网络损耗和提升节点电压稳定性为优化与控制指标，提出一种融合天牛须搜索与吸引排斥和双向学习双重策略的改进式粒子群算法应用于分布式可再生能源并网系统的优化方案。通过仿真结果分析与对比可知，所提改进式粒子群算法进行无功补偿优化可降低配电网整体有功损耗和电压波动，提升系统电能质量。相较于传统粒子群无功优化算法，改进式粒子群算法可显著提高运算效率。

进一步地，应用本文算法有利于为配网侧制定更优无功配置策略，增强分布式可再生能源接入配电网后系统运行的稳定性，提升配电网的经济性水平。通过现有设备协调完成能源结构的优化，提高了分布式能源利用率，为进一步含分布式可再生能源的配网系统无功优化提供了参考和借鉴。