常态课中渗透“数学学习策略”的实践和感悟

周建平

(浙江师范大学附属中学,浙江 金华 321004)

当下，有关中小学教育的国家“顶层设计”密集出台以及“疫情”的影响在逐渐改变中小学教育、教学的传统范式.随着“双减”的逐渐落地，学生的数学学习更需要自觉，更需要内驱力.事实上中小学数学教育在多年的“应试”浸润中，大部分学生早就失去了学习兴趣，或者说已经不会“真正地学习”，这一现象尤其是在高中数学学习中表现更为突出.笔者曾对2021级部分高一新生进行了数学学习策略问卷调查，通过对问卷结果科学分析发现：在生源基础较好的前提下，多数学生对数学学习策略知之甚少，平时学习过程中根本没有主动运用“策略”的想法和意识，更谈不上灵活运用策略.数学教师可以在常态课中主动渗透数学学习策略，这既是当前形势的需要也是培养学生数学核心素养的需要.

1 什么是数学学习策略

目前“数学学习策略”在学术界还没有形成统一的认识.在研究相关文献和资料的基础上，从理论与实践相互促进的角度，笔者给出对“数学学习策略”的浅显认识，数学学习策略就是对数学学习方法、技巧等的选择和使用.学生能适当地运用数学学习策略，就是能根据特定的学习情境在自己的储备系统中选出合适的学习方法和技巧等，以便使自己的解题和学习境界达到更高的层次.数学学习策略具有一般学习策略的特点(如：学习计划的制定、思维导图的运用、记忆方法的选择等)，它也有自己鲜明的特色(如极值点偏移问题的处理策略：对称构造函数+主元法；比值、差值设参；对数平均不等式的运用等).

2 课堂教学中的数学学习策略

“课堂教学”是渗透“数学学习策略”的主阵地之一.分类讨论是学生必须掌握的数学思想之一，笔者在教学中讲解相关题目时,通过一题多解让学生体会数学策略的魅力.

例1已知函数f(x)=ex-ax2,其中a∈R，若f(x)在(0,+∞)内单调递增，求实数a的取值范围.

方法1(分类讨论法)由f′(x)=ex-2ax，其中a∈R，可知f(x)在(0,+∞)内单调递增，即f′(x)=ex-2ax≥0在(0,+∞)上恒成立.又f″(x)=ex-2a.

1)当a≤0时，f″(x)=ex-2a≥0恒成立，即f′(x)在(0,+∞)上单调递增，从而f′(x)min>f′(0)=1≥0.

2)当a>0时，由f″(x)=0，得x=ln 2a.

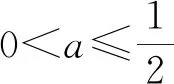
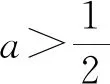
表1 x，f ′(x)，f ″(x)的变化情况

从而f′(x)min=f′(ln 2a)=2a-2aln 2a

=2a(1-ln 2a)≥0,

于是

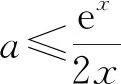
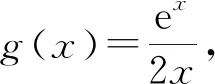
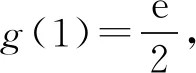
设置本例的目的是让学生感悟：在思考过程中具有“策略”意识，可以避免过多的分类讨论.这是数学学习策略在解题实践中的现实运用.又如排列组合问题中的“捆绑法、插空法、优限法”也是渗透数学学习策略的绝好素材.

在日常课堂教学中，教师要不断地进行学习策略的渗透，这样学生对数学学习策略的领悟会更深，进而能从认识、认同数学学习策略逐渐过渡到自己能运用策略并能总结策略.数学学习策略的渗透要讲究实效，要审时度势，以生为本.不同的数学学习策略、不同的教学对象、不同的渗透时机等都使得日常教学变得异常复杂，笔者对每节课的策略渗透设计都要慎之又慎.大量的教学实践告诉我们：数学学习策略的渗透要讲究实效.教学中要有真实的数学学习问题，尤其是高考必考的热点和难点，当学生苦于没有好方法来理解和掌握时，在数学学习策略的渗透下难题变得“唾手可得”，学生自然会接受相关的数学学习策略.在此情境下，教师要不失时机地给学生传授此种数学学习策略的详尽步骤和要点.在日常学习策略渗透教学中多设计一些此类问题，相信学生更能心悦诚服地接受和运用学习策略.

3 关于数学学习策略的几点思考

3.1 好的“教学预设和生成”更有利数学学习策略的整体、无痕渗透

好的“教学预设和生成”可以让学生很自然地“触摸”到数学学习策略.笔者把“函数图像的理解和综合运用”的教学过程变成渗透数学学习策略的不可多得的时机，在层层递进的思考下，学生对数学学习策略会有更深的感悟.下面是笔者的部分课堂教学设计、实录和感悟,与同行分享.

实录1分别作出下列函数的图像：

1)y=|lgx|;

3)y=x2-2|x|-1;

实录2请同学们思考下列问题，并尝试证明.

1)函数图像平移变换八字方针：

①“左____右____”，要注意加减指的是______；

②“上____下____”，要注意加减指的是______．

2)对称变换：

①f(x)与f(-x)的图像关于______轴对称；

②f(x)与-f(x)的图像关于______轴对称．

升降施工平台为高层建筑外墙施工用的安全防护、工人操作和解决楼层水平运输的操作平台，平台配合升降系统使用可进行提升和下降操作[1-2]。在使用状态时，施工平台依靠附墙导座与建筑外墙固定连接；在升降状态时，施工平台脚手架的导轨与附墙导座进行滑道配合升降。

3)翻折变换：

①|f(x)|的图像是将f(x)的图像中x轴______的图像对称翻折到x轴______，x轴______的图像不变；

②f(|x|)的图像是f(x)的图像中x轴______侧的图像不变，再对称翻折到y轴的______侧得到．

4)关于两个函数图像对称的3个重要结论：

①函数y=f(x)与y=f(2a-x)的图像关于直线______对称；

②函数y=f(x)与y=2b-f(2a-x)的图像关于点______中心对称；

③若函数y=f(x)定义域内的任意自变量x满足f(a+x)=f(a-x)，则函数y=f(x)的图像关于直线______对称．

5)函数图像自身的轴对称：

①f(-x)=f(x)⟺函数y=f(x)的图像关于______轴对称；

②函数y=f(x)的图像关于______对称⟺f(a+x)=f(a-x)⟺f(x)=f(2a-x)⟺f(-x)=______；

③若函数y=f(x)的定义域为R，且有f(a+x)=f(b-x)，则函数y=f(x)的图像关于直线x=______对称．

6)函数图像自身的中心对称:

①f(-x)=-f(x)⟺函数y=f(x)的图像关于______对称；

②函数y=f(x)的图像关于点(a,0)对称⟺f(a+x)=-f(a-x)⟺f(x)=-f(2a-x)⟺f(-x)=______；

③函数y=f(x)的图像关于点______成中心对称⟺f(a+x)=2b-f(a-x)⟺f(x)=2b-f(2a-x)．

7)双对称出周期：若一个函数f(x)存在两个对称关系，则f(x)是一个周期函数，具体情况如下(假设b>a)：

①若f(x)的图像关于x=a,x=b轴对称，则f(x)是周期函数，周期T=______；

②若f(x)的图像关于点(a,0),(b,0)中心对称，则f(x)是周期函数，周期T=______；

③若f(x)的图像关于x=a轴对称，且关于点(b,0)中心对称，则f(x)是周期函数，周期T=______.

实录3学以致用.

练习1(多选题)函数f(x)的定义域为R，若f(x+1)与f(x-1)都是奇函数，则

( )

A．f(x)是偶函数 B．f(x)是奇函数

C．f(x)=f(x+4) D．f(x+3)是奇函数

答案C,D.

分析因为f(x+1)与f(x-1)都是奇函数，所以函数f(x)的图像关于点(1,0)及点(-1,0)对称，从而

f(x)+f(2-x)=0，f(x)+f(-2-x)=0，

故

f(2-x)=f(-2-x)，

函数f(x)是周期T=2-(-2)=4的周期函数，选项C正确．又因为f(-x-1+4)=-f(x-1+4)，即f(-x+3)=-f(x+3)，所以f(x+3)是奇函数，选项D正确．故选C,D．

通过环环相扣的3个环节，让学生感悟到数学学习是需要基础的，无论是概念的学习还是解题能力的提升都需要前面的基础，环环相扣,缺一不可.对“直接法和图像变换法”等基本知识熟练掌握后，还要进行升华.所谓“升华策略”是指学生主动整合各种资源进行精细的反思和升华，从而能更好地解决新的问题.如果不总结、不升华，那么前期付出的思考就失去了应有的价值，升华了的策略和方法是学生可以顺利应用的秘籍.学生通过多选题目的思考会清醒地认识到：知识方法升华到什么程度，解法就简洁到什么程度.好的“教学预设和生成”可以使学生在认知、记忆、领悟、运用过程中，感知、领悟学习策略和方法给学习带来的微妙的升华作用.其实在教学过程中，教师不需要给学生点明什么是数学学习策略、运用了什么学习策略，这些对学生并不重要，重要的是学生在教师创设的情境和解决问题的过程中，有了新的体验、新的感悟，感受到数学学习的乐趣，能够“见贤思齐”，能够学以致用就可以了.

在日常教学中，教师要尊重学生内心的真实体验，尊重学习策略形成的规律.好的教学一定会使学生身心愉悦.渗透数学学习策略绝不能一厢情愿，要多观察学生的课堂表现，多和学生交流、谈心，尊重他们的主体体验，教师不要夸夸其谈学习策略的高妙之处，要分析学生能不能接受、能不能用得上.学生能把相关学习策略内化到自己的认知结构中，最后形成自己的学习智慧和技能，并能在后继的学习中灵活运用并发扬光大之，这应是教学的最高境界.

笔者在渗透数学学习策略教学实践时，根据相关数学学习策略的特质，分为以下3个阶段：在数学学习策略尝试阶段，要让学生在实际解题过程中，牛刀小试，颇具成就感；在数学学习策略的固化阶段，要让学生主动地运用学习策略，能够固化成学生的一种习惯，让学习策略成为学生的主观自觉行为；在数学学习策略的升华阶段，恰如其当的学习策略会给学生的思维和身心带来愉悦，在教学中，教师要让学生感受：由于学习策略的使用和灵活掌握，自己的数学学习是充满了内省与体悟的智慧活动，自己是学习的主人.由于数学学习策略各有不同，教师要根据学生的心理特点、学业基础等来整体把握、统筹安排不同策略出现的时机和教授难度，不要急于求成.数学学习策略的形成是循序渐进的，教师在每一个环节都要刻意设计，助学生一臂之力，让学生顺利接受、内化、灵活运用相关学习策略.

3.2 数学学习策略的渗透要日常化

我国中学生在日常数学学习中有很多良好的习惯，如预习、课后复习、练习等，在笔者看来这其中就包含着数学学习策略.我们在教学中不能只关注所谓的“高大上”的数学学习策略，一定要把日常学习常规和学习策略结合起来，如画“三角函数和差倍半公式思维导图”是一种好的数学学习策略，但如果没有日常对每个公式的“刻意训练、各个击破、举一反三”，这种思维导图学习策略效果不会很好.只有学生养成良好的日常学习习惯，教师的学习策略渗透才不会成为空中楼阁.

在学生高中三年的学习过程中，教师要多观察、多研判，在学生“思穷”“技穷”时，点拨之“学习策略”，学生会受益无穷.如在高一数学初始课，笔者会利用教材中相关素材，如2019年人教A版《数学(必修1)》中的“主编寄语”，字里行间充满了数学学习策略，笔者借机对学生进行学习策略的渗透.在与高一学生聊天时，笔者会告诉学生：“高中数学变得抽象了，更需要学生和家长有静气.数学的学习没有什么灵丹妙药，如数学运算能力的提升，就要通过持之以恒‘有智慧、有反思’的数学运算实践来解决.高中的学习不要好高骛远，要明确数学能力的提升是循序渐进的，不要被‘教辅’‘课外辅导班’等所左右；不要在高一做高三的题目，在高三再补高一对概念的认识和领悟.”在与高三学生聊天时，笔者会告诉学生：“对经典例题要慢慢揣摩、领悟，要一题多解、多题一解，领悟题目的数学思想方法，不能囫囵吞枣迫不及待地跳入‘题海’.”事实证明：急于刷题，刷掉的是学生对数学的乐趣，刷掉的是学生学数学的灵气.

3.3 数学学习策略的渗透要注重分层，尤其要关注学生主体的差异性

近年来，高中学生在知识储备、学习力(学习动力、学习能力、学习毅力和学习创新力)、学习习惯等方面表现出较大的个体差异性.比如笔者所在的学校，生源特殊，有普通班、浙师大直升班、中新班、青海班等，班级差异性大，即使同一班级内的学生，差异性也较大.在进行数学学习策略渗透时，教师就要多关注这种差异性.笔者根据“知识储备、学习力、学习习惯”这3个维度对学生进行合理分层，采取不同的渗透策略，尽可能使每一个学生都能得到数学学习策略的升华，获得成功的愉悦.分层渗透的目的不是“放弃”而是不“抛弃”.

总之，数学学习策略的渗透应不露痕迹，这样才能让学生达到“自然化之、自然而用”的最高境界.学生“数学学习策略”的养成和应用是一个长期、持久的过程，相信通过教师坚持不懈地进行数学学习策略渗透，学生定能从数学学习策略的“必然王国”迈向“自由王国”.