通法结构筑能力 思维进阶育素养——一道不等式统测题的解与思

王 凯, 顾予恒

(1.源清中学，浙江 杭州 310015；2.浙大城市学院附属高级中学，浙江 杭州 310015；3.杭州第二中学钱江学校，浙江 杭州 311215)

不等式是高中数学学习的基础和关键，它贯穿于整个高中数学的方方面面，也是解决很多疑难问题的重要工具.在不等式的教学过程中，教师一定要注重思维方法的培养，掌握合理有效的思维方法是提升学生问题解决能力的有效途径.本文以2021学年第一学期浙江省杭州市高三数学质量检测第16题为例，谈不等式解题教学中培养和落实学生数学核心素养的做法和思考．

这个题目题干简洁，蕴涵了丰富多彩的代数变换策略和技巧.不同程度的学生对这个问题的解决会有不同的认识层次，但在解决问题的过程中都能对学生理性思维的培养起到作用，发展其思维，培育核心素养．

层次1多参变单参，函数显威力，数学运算是工具.

分析题干中给出了两个正实数满足的一个条件(x2+9y2=1)，目标是求一个代数式的最值．事实上，等式为变量之间建立了联系，借助条件可以通过适当的方式减元.

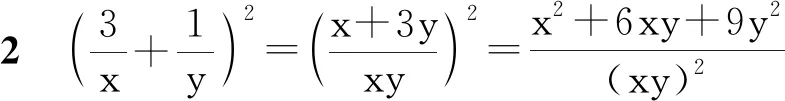
目标转变为二次型函数求值域的问题.

又因为1=x2+9y2≥6xy，所以

即

t≥6，

从而

得

还可以从结构入手，由于x2+9y2=1是齐次式，故可采取比值换元，得策略3.

策略3令y=kx，可得

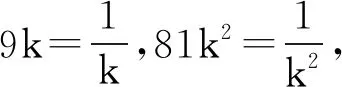
方法提炼对于双变量最值问题，我们通常可以根据代数结构和知识储备找到合适的方式将其变为单变量函数问题来解决．“能够在关联的情境中确定运算对象，提出运算问题”是《普通高中数学课程标准(2017年版2020年修订)》(以下简称《新课标》)对数学运算素养水平二的要求．在日常的解题教学中教师应加强通性通法的教学，教会学生关联情境，把问题变回到熟悉的数学情境中，然后建立合适的运算思路，从而解决问题.这是培养学生理性思维、落实数学运算核心素养的抓手．

层次2双参巧变点，图像来帮忙，直观想象是策略.

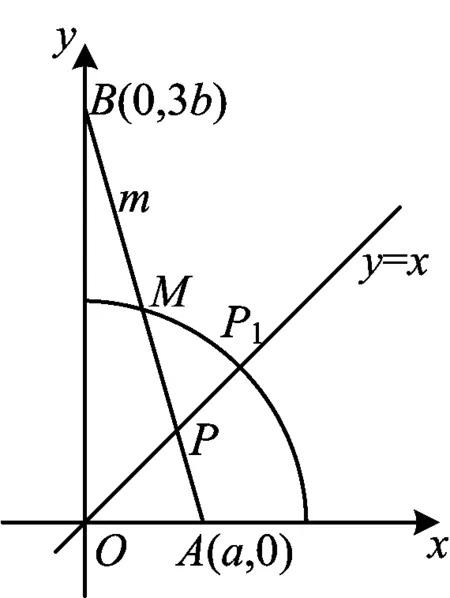
图1

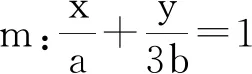
方法提炼“能够在关联的情境中，想象并构建相应的几何图形”是《新课标》对直观想象素养水平二的要求．在日常的教学中教师应抓住各种机会引导学生形成数形互助的意识，能够用图形探索问题解决的思路，进而形成数形结合的思想，体会几何直观的作用和意义.

层次3基本不等式，条件要满足，逻辑推理是思想.

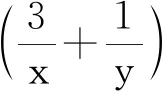
可以尝试用不等式工具来解决问题.

从而

可得

故

基本不等式是解决最值问题的一个重要工具，但使用基本不等式对学生的能力要求较高，尤其要关注取到等号时的条件.若某个问题的解决过程中多次用到基本不等式，则一定要检验等号取到的条件是否一致.若不一致，则可能要另谋他法.

方法提炼通过问题的表征去寻求知识背景，符合《新课标》对逻辑推理水平二中提出的：能够对与学过的知识有关联的数学命题，通过对其条件与结论的分析，探索论证的思路，选择合适的论证方法予以证明，并能用准确的语言表述论述过程．通过问题的表征联想“熟悉”的配方，就是培养学生从方法层面去考虑问题解决策略，逻辑推理的核心素养也在这个过程中落地生根.

层次4借助高观点，结构很重要，数学抽象是素养.

除了基本不等式外，高中阶段有些拔尖的“数学精英”也会接触一些高等数学观点下的不等式，借助这些不等式也能处理这个问题.区别是此时工具不等式更抽象了，需要学生有较高的数学抽象素养才能够理解.下面给出3个高观点下的解决策略.

策略7柯西不等式的二维形式:

(ac+bd)2≤(a2+b2)(c2+d2)，

当ad=bc时，等号成立.

由柯西不等式可得

(x+3y)2≤[x2+(3y)2](12+12)=2，

即

即

从而

策略8权方和不等式：若ai>0，bi>0，m>0，则

成立，当ai=λbi(其中i=1,2,…,n)时，等号成立.因此

≥a1b1+a2b2+…+anbn

两边同时立方后得

即

方法提炼能够通过数学对象、运算或关系理解数学的抽象结构，能够理解数学结论的一般性，能够感悟高度概括、有序多级的数学知识体系是《新课标》对数学抽象水平三的要求.这个要求不是所有学生都要具备的，但对那些拔尖的“数学精英”还是需要的，也是在为我们的未来培育“创新”性人才.

结束语在数学解题教学中，我们要重视通性通法的运用，让学生会处理数学结构，培养其解决问题的能力.同时还要教学生从不同层次来思考问题，解读好数学学科知识，挖掘数学知识背后的思维层次，不断促成学生思维的进阶，最终实现学生数学核心素养的养成.