跨线龙门吊吊装小箱梁全过程力学性能分析

彭伟，曾珍明，孟庆锋，王培桥，王国俊

（中交第四公路工程局有限公司，北京 100000）

0 引言

龙门吊作为一种大型吊装设备，在工程中应用较为广泛。龙门吊由早期的实腹梁转变为现今的钢桁架形式，以减轻自身重量，实现较大的跨度和安装的便捷性。由于龙门吊需要满足较大的吊装能力和较高的工作效率，故对其力学特性有很高的要求[1-7]。

目前，许多学者对龙门吊的力学特性及吊装技术做了许多工作。李晋文等人[8]基于龙门起重机的动力学模型研究了主梁受力特点，并校核了起重机刚度及强度。刘铁军等人[9]通过有限元模型对大修列车龙门吊的静强度和模态特性开展了研究。张文韬等人[10]通过数值模拟高低腿龙门吊的受力和变形，发现最大竖向位移出现在主梁二分之一位置处。商大勇[11]则研究了龙门吊在移动荷载作用下对基坑围护结构和土体受力和变形的影响。然而，关于龙门吊在重物起吊全过程的静动力特性的研究并不多。

基于此，本文以某城市双层多幅小空间高架桥预制小箱梁架设为背景，研究了小箱梁离地阶段、均匀提升、横向错位行走等工况下的静力性能，依托动力学分析理论开展跨线龙门吊的动态特性分析，并通过模态分析得到跨线龙门吊振动特性。

1 龙门吊结构参数

本次吊装所用的龙门吊主要由主梁、柔性支腿、刚性支腿、小车组成。主梁的总跨度为39m，净高22m，吊装额定90t。主梁采用双梁结构形式，间距为2.5m，支腿的基距为12m，主要材料为Q235钢。

2 吊装过程有限元分析

2.1 龙门吊参数化模型建立

为便于模拟多种吊装工况，有限元模型采用ANSYS宏文件的形式建立参数化模型。吊车梁和小箱梁均采用beam188单元，支腿的底部边界采用固端约束。考虑到小车、箱梁和吊车梁同时建模时，较难以收敛，因此本文将分开考虑，即先建立小箱梁的模型，根据小箱梁的荷载提取两个吊点的支反力，并作为作用于吊车梁上的荷载，小车也用节点力考虑，以进行吊车梁静动力分析，龙门吊的有限元模型如图1所示。

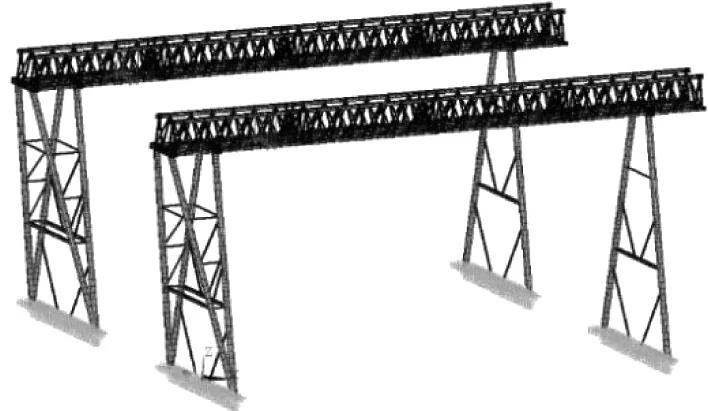
图1 龙门吊有限元模型

2.2 有限元分析

小箱梁的提升过程主要分为离地阶段、均匀提升阶段以及小车行走阶段，由于空间限制，还需要将小箱梁横向错位。因此，本文将考虑上述4种工况吊车梁的静力特性，并依托动力学和瞬态分析，研究龙门吊的振动特性。

在进行各工况分析前，需对小箱梁进行静力分析。先建立小箱梁模型，进行网格划分后，对其施加重力荷载，得到吊点的支反力。其中，2 个吊点的位置根据吊点弯矩与跨中弯矩相等原则确定，为距离梁端0.207倍的梁长。

2.2.1 离地阶段

本文选择完全瞬态分析方法进行，阻尼形式为Rayleigh，阻尼系数α=0.16，β=2.14。将吊点支反力时间历程结果作为载荷，施加在龙门吊上，进行瞬态动力学分析。

图2 为跨中位置处的位移-时间历程曲线，跨中位移震荡衰减较快，在20s 左右达到平稳状态，此时跨中位移稳定在平衡位置附近，位移大小为5.5mm。但最大位移并非在跨中，而是在跨中左侧14mm 处，其平衡后的位移大致为12.5mm（如图3 所示）。本工况下的最大应力出现在柔性支腿的顶部（如图4 所示），应力大小为188MPa。选取此处节点作为应力热点，获取其应力时间历程曲线如图5所示，应力值经过一定的震荡后稳定在188MPa附近，但瞬时的应力接近300MPa，大于结构的允许应力。为防止可能的安全隐患，应在此处进行补强。

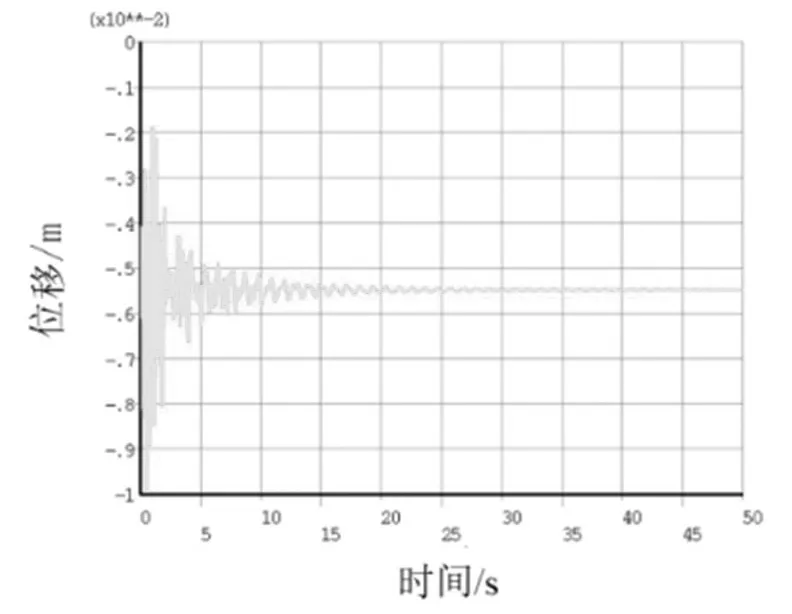
图2 跨中位移-时间历程曲线

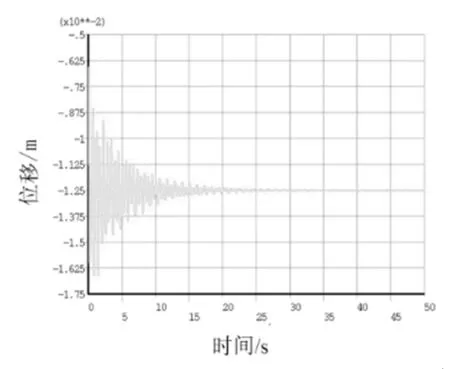
图3 最大位移-时间历程曲线

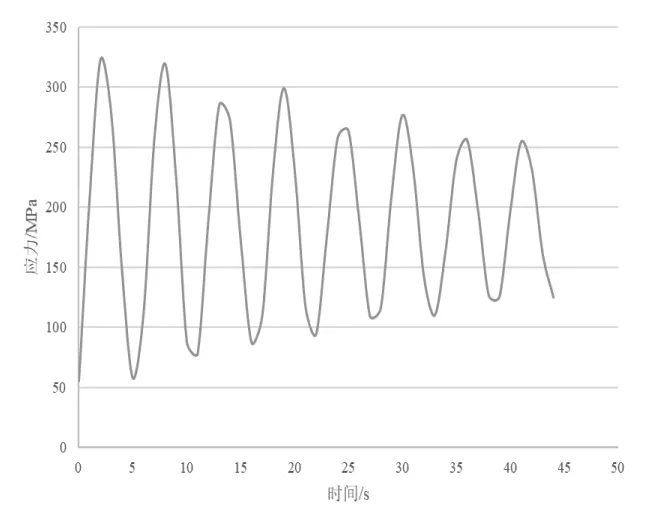
图5 应力最大值的时间历程曲线

2.2.2 均匀提升

此阶段小箱梁对吊车梁的作用与静力平衡状态类似。将小箱梁的重力响应求解后得到吊点的支反力为398kN，龙门吊的应力如图6 所示，小车在刚性支腿提升过程中，刚性支腿与柔性支腿的末端的应力都比较大，最大应力为188MPa。

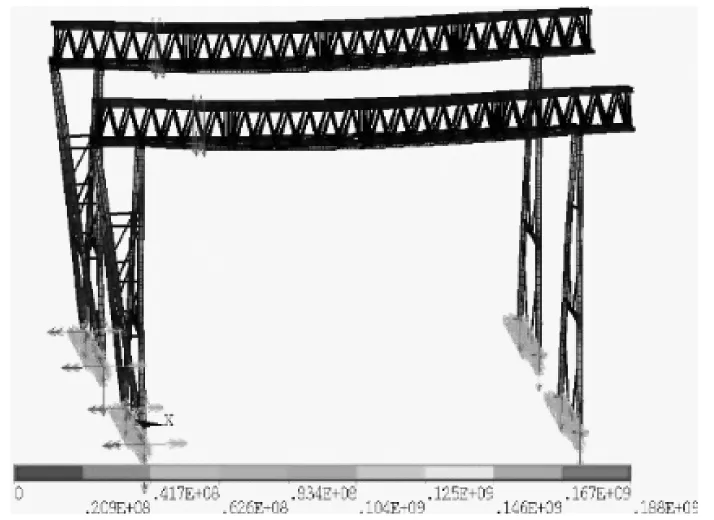
图6 吊车梁应力图

2.2.3 小箱梁非错位状态下小车行走

小箱梁提起以后，以匀速状态行走时整体仍处于平衡状态。对小车实时行走进行瞬态分析，得到跨中的位移时间历程（如图7 所示），随着小车的移动，跨中位移呈先增大后减小趋势，在14s 左右达到最大位移20mm，由此可见此时对主梁的冲击最大。最大的应力仍出现在柔性支腿的顶部，经过一段时间震荡后，也逐渐稳定在188MPa 附近，瞬时应力也超过了容许应力，需进行适当加强。

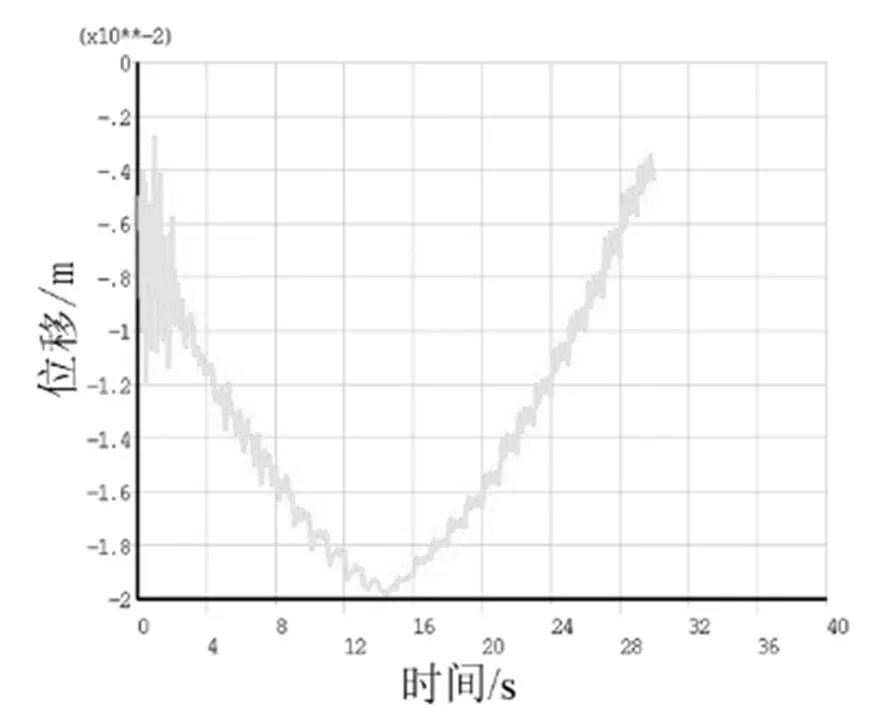
图7 跨中位移-时间历程曲线

2.2.4 小箱梁错位状态下小车行走

小箱梁错位状态下（5°），两个吊车梁跨中处的位移时间历程曲线如图8 所示。两个位移的变化规律均呈先增大后减小规律，由于吊点2 离跨中更近，故其位移在12s 时达到最大值，吊点1 需要14s，但位移的大小均为20mm。而吊车1 的应力最大值达到了196MPa，吊车2 的应力最大达到了212MPa。由此可见，在错位状态下吊车梁的应力将增大。随着错位角的增大（5～15°），达到最大位移的时间逐渐缩短，但吊车2 最大的应力值呈现先减小后增大的趋势（见图9～图10）。

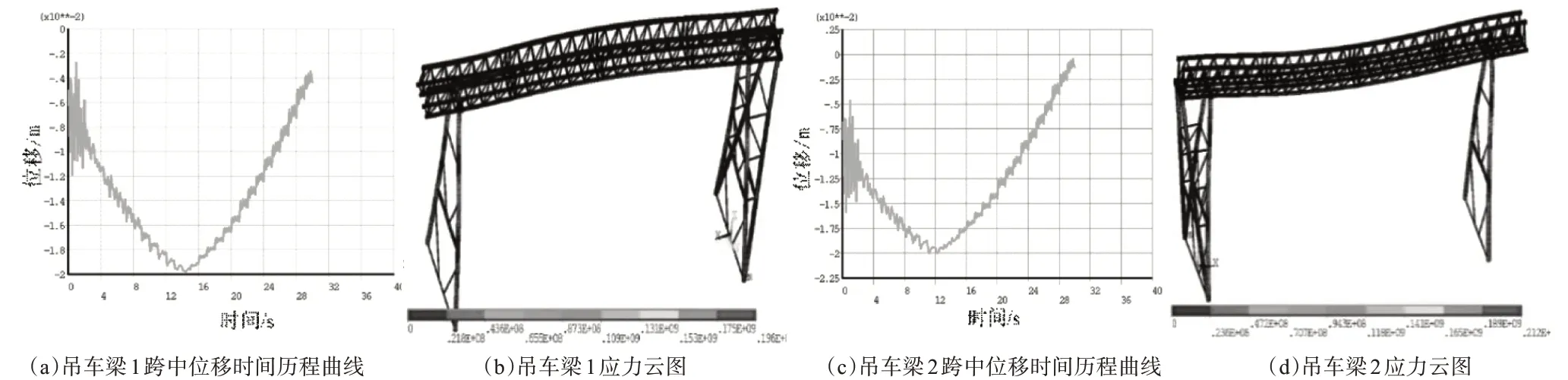
图8 错位角为5°的力学状态

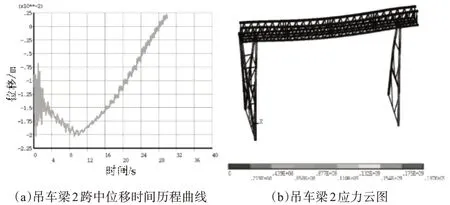
图9 错位角为10°的力学状态

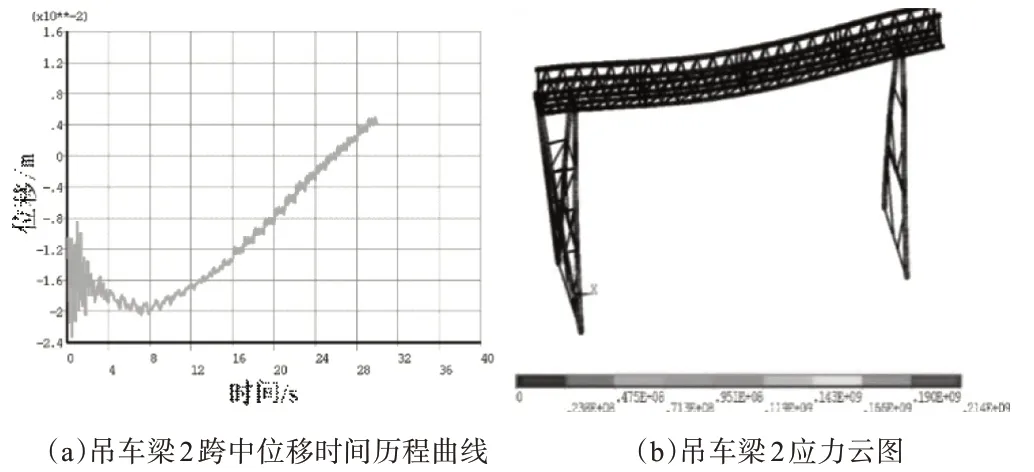
图10 错位角为15°的力学状态

2.2.5 模态分析

为确定龙门吊的振动特性，需研究系统的模态响应。计算时采用Block lanczos 法，由于阻尼的作用高阶模态衰减较快，其贡献较小，故只考虑前6阶的低阶模态，各阶的频率与振型见表1和图11所示。对前6阶振型图分析可知，第1、6阶振型揭示了水平方向的振动，原因可能是小车的启动或者制动；第3 阶振型为Y 方向，可能是由于吊车梁的启动或者制动；第2、4、5阶振型为Z 方向，可能是由于主梁在该方向的摆动较大，是吊车梁的薄弱环节。

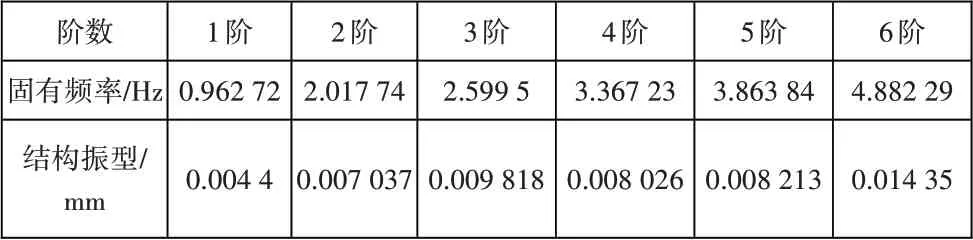
表1 前6阶模态

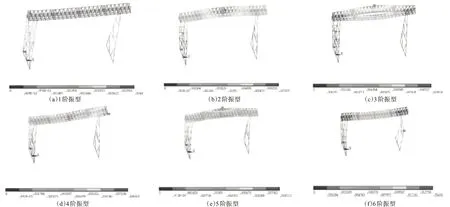
图11 振型模态

3 结论

本文以某城市双层多幅小空间高架桥预制小箱梁架设为工程背景，基于有限元模型分析了龙门吊提升小箱梁的静动力特性和模态特征，得到以下结论：

（1）研究了小箱梁提升过程四个阶段的静动力分析，发现位移最大位置为跨中附近处，最薄弱的地方为柔性支腿的顶端；在错位状态下吊车梁的应力比非错位状态下的应力更大，但随着错位角的增加，应力呈先增大后减小趋势。

（2）模态分析表明，小车与吊车梁的启、制动均对吊车梁的振动有显著影响，竖直方向的振动是其薄弱环节。