基于分位数回归的交通流速度-密度关系随机基本图模型

潘义勇，管星宇

(南京林业大学 汽车与交通工程学院，江苏 南京 210037)

0 引 言

速度-密度关系基本图模型是交通流理论的基础，挖掘两者之间的关系有利于在交通状态识别、交通拥堵分析等领域发挥重要的作用[1-2]。现有的研究主要集中在速度-密度关系确定基本图模型，由于交通流具有固有的随机特性和异质特性，确定性的速度-密度关系限制了其表征实际交通流的能力，导致在交通控制策略建模中产生误差[3]。因此需对交通流速度-密度关系随机基本图模型问题进行研究。

针对速度-密度关系确定基本图模型研究很多，自从Greenshields模型首次提出以来，其缺点是密度值较大或较小时，模型拟合效果较差，在此基础上改进的模型有：Greenberg模型，Underwood模型，Northwestern模型，Newell模型，这些模型都是单阶段确定性模型[4]，多阶段模型这里不再阐述。在对速度-密度确定关系模型参数进行拟合过程中，主要存在两个问题：数据点低密度状态下的分布较为密集，导致均值回归受异常点影响较大；实测的速度、密度值具有随机性，在对数据进行均值回归时，难以满足方差齐性和正态性的假设要求[5]。

针对速度-密度关系随机基本图模型的研究非常少，S.E.JABARI等[6]、S.FAN[7]分别针对特定的交通流模型推导了速度概率分布函数和密度的关系模型，但是该方法不能推广到其他交通流模型；X.QU 等[8]提出基于不同百分位的交通流速度-密度关系基本图模型，根据不同的百分位点采用加权最小二乘法对不同的百分位点进行参数拟合获得关系模型，但是该方法从根本上还是采用最小二乘法进行参数拟合，异常值对拟合效果影响较大。

针对以上问题，引入分位数回归获得速度-密度关系随机基本图模型[9]，分位数回归在计量经济学中已经获得了广泛的应用，分位数回归采用最小一乘法进行参数拟合，对异常值具有更好的鲁棒性，更能反映数据整体的分布状况,更全面的反映数据信息,适用性更广，有利于对交通流数据的深度挖掘，这是笔者研究的出发点。首先，基于分位数回归建立交通流速度-密度关系随机基本图模型；其次，利用分位数回归对实际交通流数据进行速度-密度曲线参数拟合，获得不同分位数水平的速度-密度曲线簇；第三，对参数值进行了假设检验和置信区间的计算，并对拟合结果进行数值分析；最后，总结了笔者的研究成果以及进一步研究的方向。

1 随机交通流基本图模型

1.1 分位数回归

分位数回归在高级计量经济学中已经获得了广泛的应用，根据不同的分位点得到对应的回归方程，可以直观的描述自变量对因变量分布的变化[10]。式(1)表示在第τ分位点下得到的回归方程，即分位数回归模型的基本定义为：

(1)

(2)

1.2 速度-密度关系随机模型

基于分位数回归构建交通流速度-密度关系随机基本图模型，充分挖掘数据中隐含的信息。以Greenshields模型为例，基于分位数回归模型改进的Greenshields模型可以表示为：

(3)

表1 基于分位数回归的速度-密度关系随机基本图模型

2 数据来源

文中的数据来源于美国德克萨斯州圣安东尼奥市的高级交通管理系统TransGuide，从中选取了2条公路进行分析：东行单向三车道的I-10公路(中间车道，传感器编号：L2-0010E-562.581)以及西行单向二车道的Loop-1604公路(第2条左车道，传感器编号：L2-1604W-034.326)，数据点在24 h内每隔20 s统计一次。在非线性模型的拟合中，为了避免数据在对数转化中出现无穷大值，保证数据分析的可靠性，对数据进行了整理，删去数据集中密度值为0的点(I-10公路第22和第628个观测值)，共获取I-10公路3 526对样本值、Loop-1604公路3 258对样本值。整理后的数据情况如表2，表2中分位差偏态测量(QSK)用于分析数据的偏态特征，QSK>0表示右偏，QSK<0表示左偏，QSK=0表示正态分布。其公式为：

(4)

式中：QSK(τ)为第τ分位点的分位差偏态测量值；Q(τ)、Q(1-τ)分别为数据第τ和(1-τ)分位点处的分位值。

表2中数据显示，I-10公路在[0.3,0.7]分位点区间的数据呈现近似正态分布的特点(QSK=0)，整个数据点的分布则呈现左偏分布(QSK<0)，说明收集到的低速数据较少。与I-10公路相比，Loop-1604公路的数据分布呈现出更为复杂的关系，但是2条公路从整体总体上都为左偏分布，图1为2条公路速度观测值的概率密度曲线，可以直观地看出2个数据集的左偏特性。图2、图3表示基于马氏距离的二维变量异常值检测分布图，考虑变量之间的相关性和数据之间的马氏距离，根据图形展示的信息，I-10公路的异常值为402个(占观测值12.3%)，主要集中于密度为[40,100]的区域；Loop-1604公路的异常值为125个(占观测值3.8%)，主要集中于密度为[60,120]的区域。结果显示：2条公路在高密度区间产生了较多的异常值，在真实的交通状况下，需要考虑这些异常值对速度变量的影响。结合分位数回归模型以及均值回归模型对异常值的鲁棒性，采用分位数回归模型更能反映速度与密度之间的关系。

表2 数据基本信息

图1 概率密度分布

图2 异常值分布(I-10)

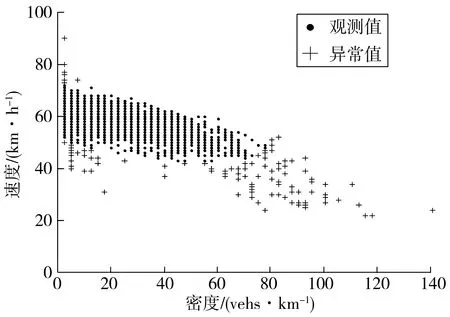
图3 异常值分布(Loop-1604)

3 数值试验

结合R语言中quanterg包中的rq函数进行线性拟合以及nlrq函数进行非线性的拟合[11]，对数据的0.05、0.1、…、0.95共计19个分位点进行回归分析，并对回归系数进行T检验得到P值，P值表示回归系数无效的概率值，用于验证回归系数是否显著(P<0.05，系数显著)。

3.1 线性模型

表3 Greenshields模型的拟合参数值(I-10公路)

图4 Greenshields模型拟合(I-10)

图5 Greenshields系数比较(I-10)

3.2 非线性模型

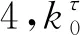
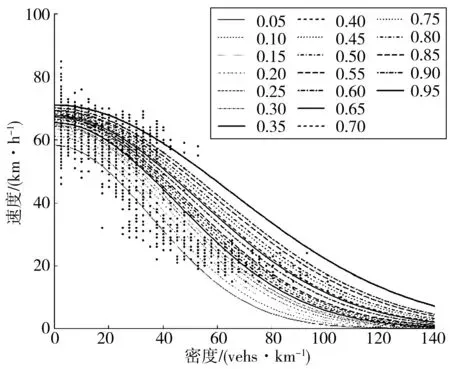
图6 Northwestern模型拟合(I-10)

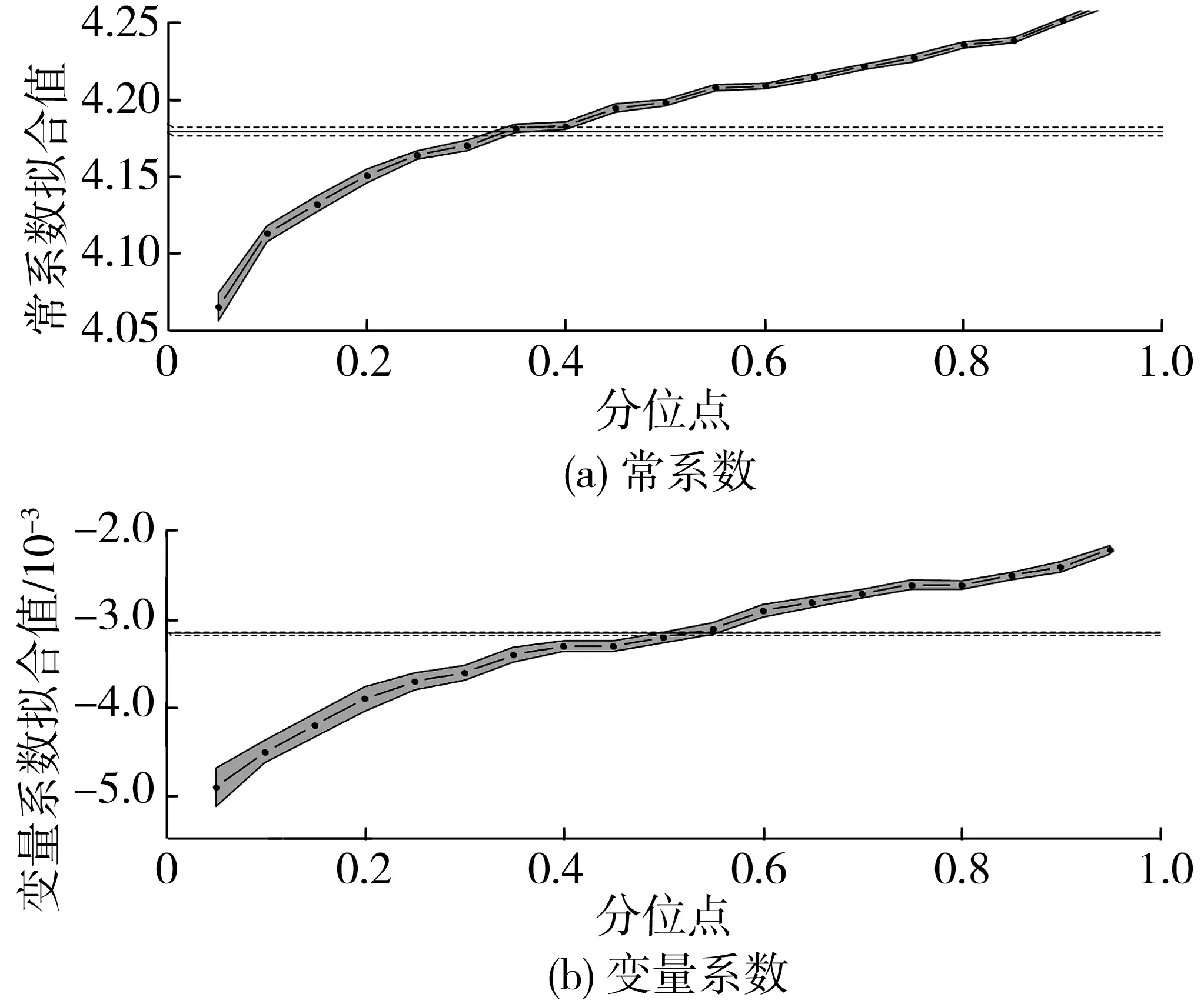
图7 Northwestern系数比较(I-10)

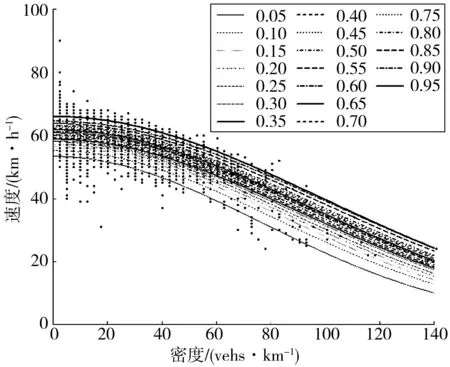
图8 Northwestern模型拟合(Loop-1604)

图9 Northwestern系数比较(Loop-1604)

图10 Newell模型拟合(I-10)

表5 Newell模型的拟合参数值(I-10公路)

3.3 结果分析

拟合结果如图11～图14，对拟合结果进行分析，得出：

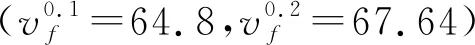
图11 Greenshields模型对比(0.5分位点)

图12 Greenshields模型误差值(I-10)

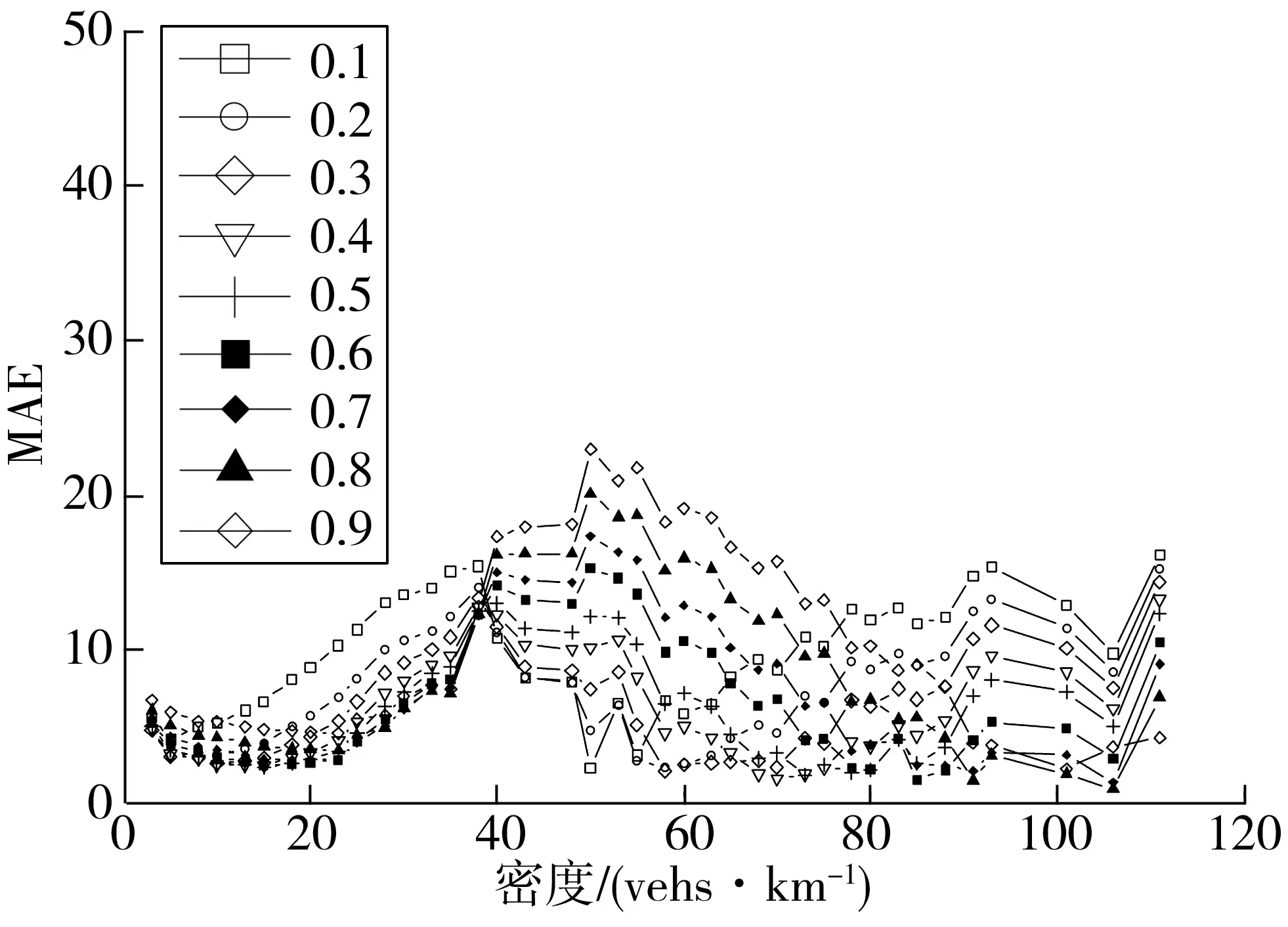
图13 Northwestern模型误差值(I-10)

图14 Newell模型误差值(I-10)

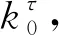
表4 Northwestern模型的拟合参数值

4 结 语

针对交通流速度-密度关系基本图问题，首次引入分位数回归获得交通流速度-密度关系随机基本图模型，利用分位数回归对速度-密度曲线进行参数拟合，获得不同分位数水平的速度-密度曲线簇，对参数值进行了假设检验和置信区间的计算，并对拟合结果进行数值分析。数值试验结果表明：相比于已有模型，笔者提出的模型可以反映不同分位数水平下交通流速度和密度的关系，更能反映数据整体的分布状况,更全面的反映数据信息，其中Northwestern分位数回归模型的误差值最小，拟合效果在上述模型中效果最好；提出的方法能够反映不同数据集的特点，适用性更广，有利于对交通流数据的深度挖掘；该模型可以应用于对交通流的建模和仿真中，不同密度值在不同的分位点对应不同的速度和加速度值，有利于提高仿真的维度和灵活性；所提出的方法为交通流基本图随机模型构建提供了一个方法论，可以推广到其他未来交通流模型。本研究只考虑了单一交通流状态下模型参数的拟合，而不同交通流状态对参数拟合结果存在很大影响，需要进一步进行研究。