变工况下基于加权理论的气阀泄漏诊断方法研究
张登路 周纪武 王 瑶,3* 张进杰,3 孙 旭
(1.北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室,北京 100029;2.中国石油化工股份有限公司金陵分公司,南京 210033;3.北京化工大学 压缩机技术国家重点实验室压缩机健康智能监控中心,北京 100029)
引 言
往复式压缩机通过曲轴连杆机构带动气缸内的活塞作往复运动,使气缸容积发生周期性变化进而实现气体的压缩和输送。大型往复式压缩机是石油化工、冶金等行业不可或缺的设备[1]。气阀是压缩机控制气体吸入与排出气缸时的关键部件。据统计,对于往复式压缩机,气阀故障是其最主要的故障形式,故障占比高达65%以上[2],因此对于气阀故障诊断的研究尤为重要。由于工艺参数的改变或节能减排的要求等限制,压缩机不能一直处于满负荷状态运行,从而使得气量调节技术在往复式压缩机中的应用越来越广泛,同时也使得压缩机的故障更加复杂多样,导致变负荷工况下的故障诊断变得更加困难。
目前国内外对于正常工况下气阀故障诊断方法的研究有很多。有研究者将示功图用于往复压缩机的故障诊断与压缩机的性能分析[3-6],也有研究者基于振动信号,将时频分析和图像识别技术相结合用于往复压缩机弹簧疲劳和阀座磨损的早期检测[7]。压缩机故障分类方法包括深度置信网络[8]、支持向量机[9]、神经网络[10]等。欧阳城添等[11]运用反向传播(BP)神经网络对压缩机故障进行检测,并与其他模型对比,结果表明该方法具有良好的稳定性。但以上这些针对往复压缩机的故障诊断方法都是在满负荷工况下进行的。赵梦芸等[12]对变负荷工况下阀片的运动规律和压缩机的气缸状态进行模拟仿真,得到了气量调节对缸内压力的影响规律。Pichler等[13]提出一种在变负荷条件下使用逻辑回归和支持向量机进行分类的压缩机气阀磨损或断裂的诊断方法。
由于变负荷工况对气阀运动特性及故障特征的影响较大,使得气阀故障特征的提取和故障的分类较为复杂,所以目前国内对于变负荷工况下气阀故障诊断方法的研究较少。本文提出一种针对变负荷与气阀故障耦合工况下气阀故障的诊断方法,利用BP神经网络,分别依据示功图的几何特征及灰度矩阵特征得到压缩机的负荷,再结合故障特征判断气阀是否发生故障;并将加权证据融合理论分别应用于负荷判断和故障分类两个过程,以提高诊断结果的准确度。
1 变负荷及气阀故障状态下示功图的变化规律
示功图是已建立的一种分析气缸内部热力学过程的方法,可以识别工业往复式压缩机的典型故障,如密封圈和气阀的泄漏、松动和颤动等。因压缩机受到的气量调节执行机构的振动冲击与气阀故障的振动发生耦合且难以分离,很难确定特征频率,而示功图能反映往复式压缩机的实时动态压力,准确地判断出压缩机的运行状态和性能,与基于振动信号分析气阀故障的方法相比,它的特征机理更加明确,可以反映设备内部的能量循环,能够在更深层次上对往复压缩机故障进行诊断。
在工业生产中,由于生产需求的改变和节能减排的要求,使得往复式压缩机不能在满负荷条件下运行。目前常用的变负荷调节方式为部分行程顶开进气阀,而负荷的变化会导致压缩机示功图的变化。同时气阀故障也会使示功图形状发生变化。通过实验与仿真数据分析得到变负荷及气阀泄漏对示功图变化的影响规律,如表1所示。
由表1可见,往复式压缩机负荷发生变化对示功图的特征影响很大,如示功图面积、压缩起始点、压缩过程线等;而当压缩机气阀发生故障时,示功图面积、压缩过程线等也会发生相应变化。因此当变负荷和气阀故障同时存在时,示功图变化规律发生耦合,导致变负荷工况下的气阀故障诊断难度增加。
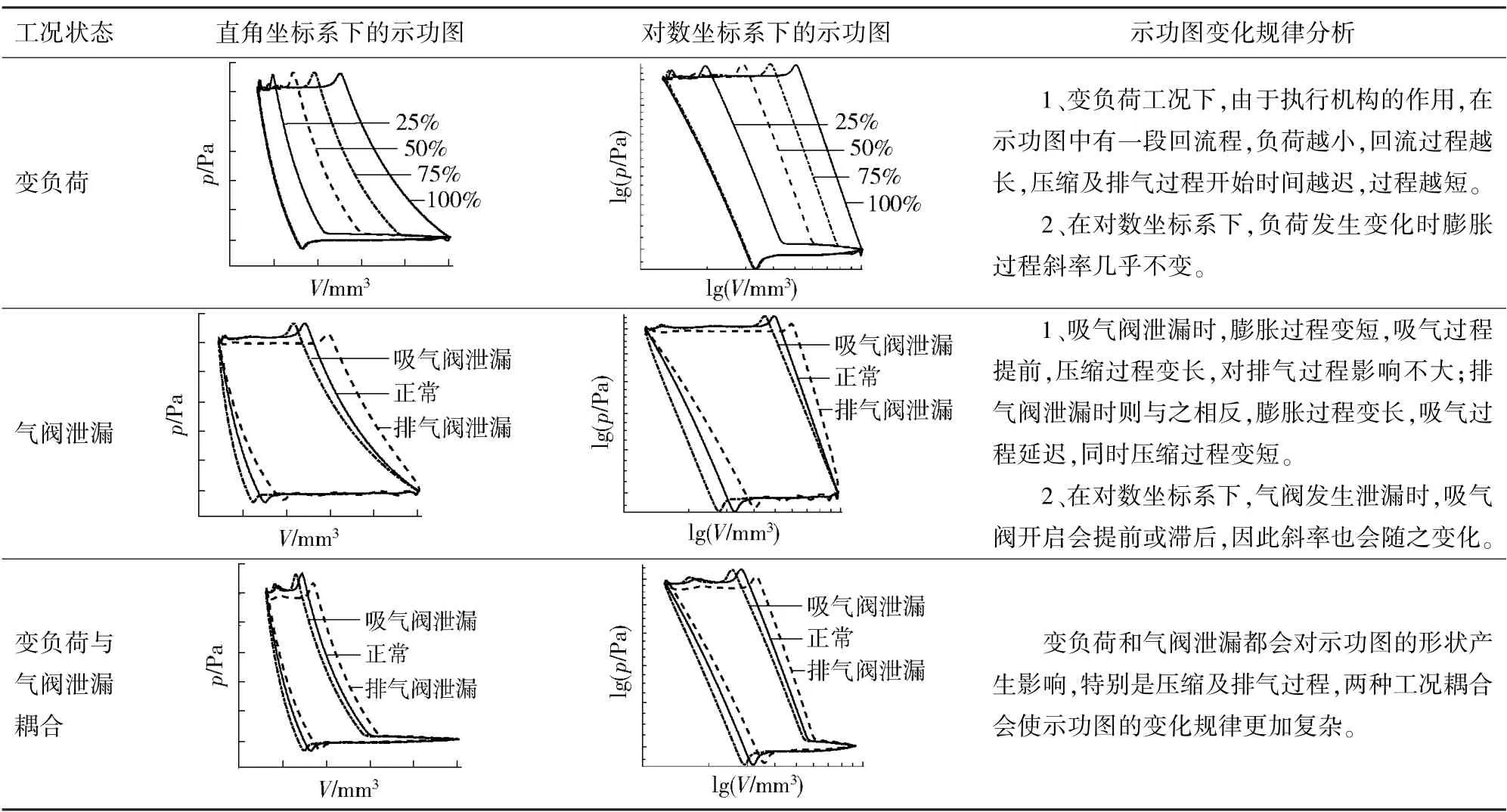
表1 不同工况对示功图的影响Table 1 Influence of different working conditions on the indicator diagram
2 变负荷工况下示功图的特征提取
2.1 几何特征
由第1节分析可知,由于变负荷、气阀泄漏等工况都会引起示功图形状的变化,因此提取了面积、形心以及主惯性矩等能反映图形变化的几何特征。
示功图面积的计算如式(1)所示。

1)形心
设示功图的一个单位面积元为dA,则对x轴静矩为

同理y轴静矩为

则示功图的形心坐标可由以下公式得到。
x轴形心坐标为

同理y轴形心坐标为

2)形心主惯性矩
x轴惯性矩为

y轴惯性矩为

惯性积可由式(8)求得。

形心主惯性矩可以通过平行移轴公式和转轴公式得到。由平行移轴公式得

式中,a为xc轴与x轴的距离,b为yc轴与y轴的距离,xc轴与yc轴为通过形心的坐标轴。由转轴公式得
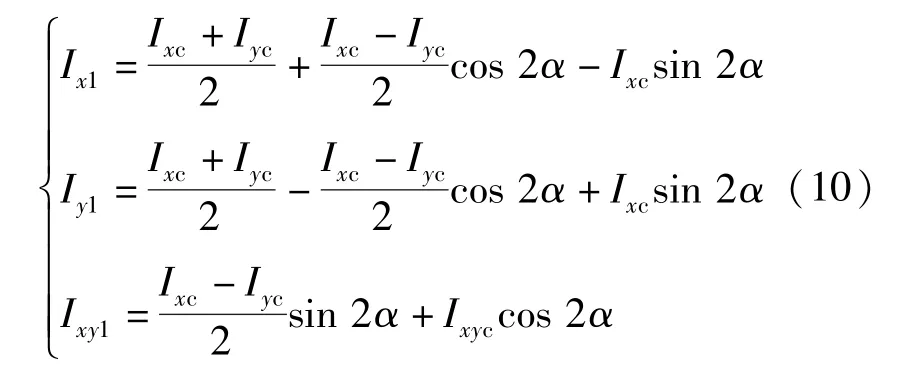
式中,α为xc轴旋转角度。当满足以下关系时,

惯性矩取得极值,且此时惯性积Ixy1=0。
变负荷工况通过部分行程顶开进气阀原理实现,利用控制卸荷器撤回时间达到调节负荷的目的,所以卸荷器撤回点位置D反映了负荷大小。


图1 几何特征值随泄漏孔直径的变化Fig.1 Variation of geometric eigenvalues with the diameter of the vent hole

图2 几何特征值随负荷的变化Fig.2 Variation of geometric eigenvalues with load
2.2 灰度矩阵特征
灰度矩阵基于网格法改进得来,网格法即是将图形放进一个矩形中,对该矩形使用网格划分,再通过这些细小网格来描述图形形状。
灰度矩阵按照等高线的方式对网格进行赋值:示功图内部网格每远离曲线1格,则其网格值增加1;示功图外部的网格每远离曲线1格,则其网格值减小1。以这种方法将整个网格填满,得到示功图的灰度矩阵如图3所示。

图3 灰度矩阵Fig.3 Gray matrix
灰度矩阵的统计特征主要有灰度均值、灰度方差、灰度偏度、灰度峰度、灰度能量、灰度熵这6个特征值。
设示功图的灰度矩阵为H(m,n),矩阵中的每一个元素hmn表示示功图灰度矩阵中的灰度值,如果所有灰度值的种类为R个,在灰度矩阵中某种灰度值r的个数为N(r),则该灰度值的概率如式(12)所示。

由式(12)可以计算灰度矩阵的6个特征值。
灰度均值为

灰度方差为

灰度偏度为
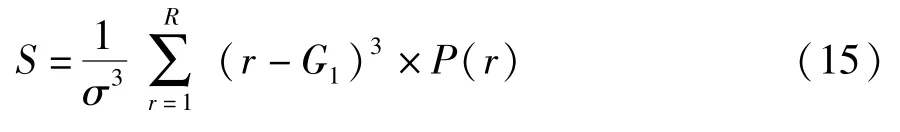
灰度峰度为

灰度能量为

灰度熵为
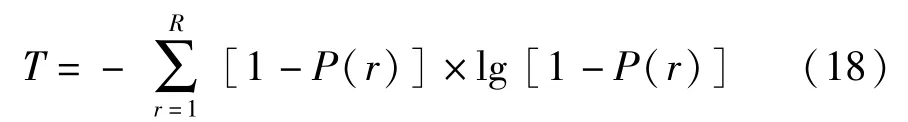
根据不同泄漏孔直径的仿真数据计算灰度矩阵征值,分析其变化规律。由图4可以看出在气阀泄漏工况下,灰度矩阵的σ2、S、G1的变化量较大,并且这种变化趋势随泄漏量的增大而增大,而E、T、P的变化量很小。由图5可以看出在变负荷工况下,灰度矩阵的σ2、G1、P的变化量较大,并且这种变化趋势随负荷的减小而增大,而T的变化量很小,E、S的变化与负荷不存在正比关系。

图4 灰度矩阵特征值随泄漏孔直径的变化Fig.4 Variation of gray matrix eigenvalues with the diameter of the vent hole
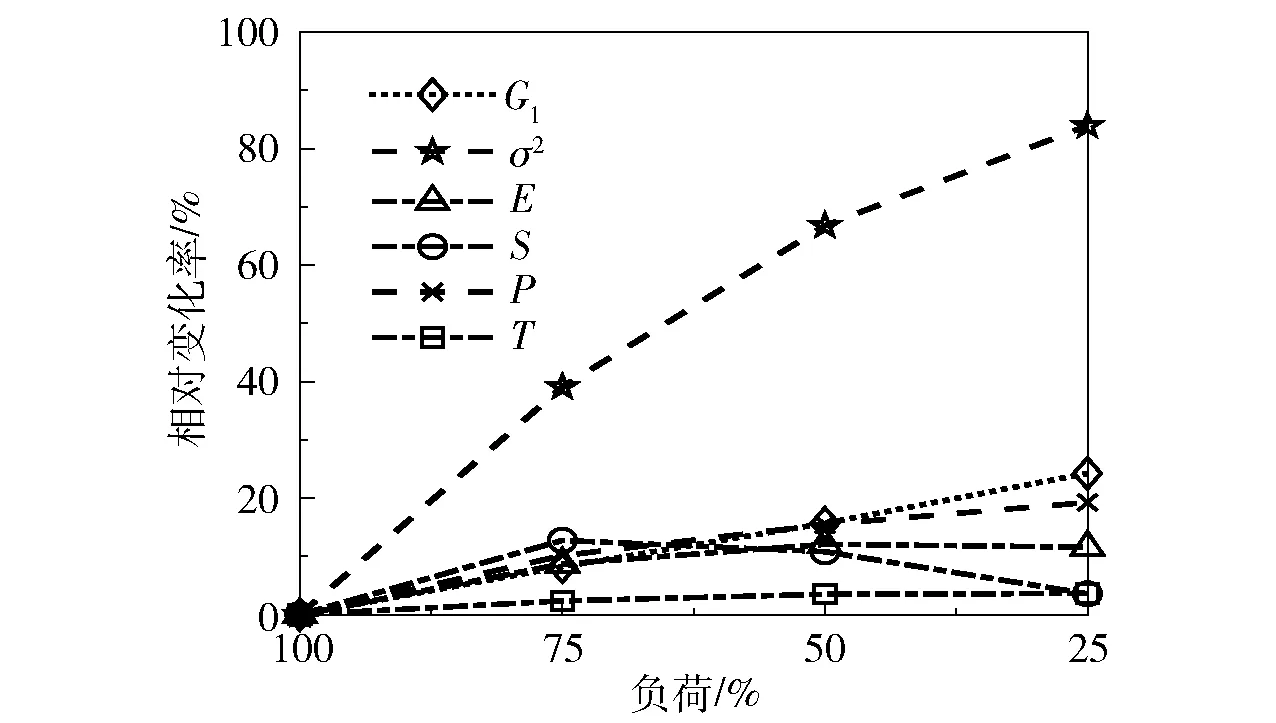
图5 灰度矩阵特征值随负荷的变化Fig.5 Variation of gray matrix eigenvalues with load
由以上分析可知,示功图的x轴形心和膨胀过程斜率k为气阀泄漏的敏感特征值,示功图的x轴形心、面积、形心主惯性矩及卸荷器回撤点为变负荷的敏感特征值;灰度矩阵的σ2、S、G1为气阀泄漏的敏感特征值,灰度矩阵的σ2、G1、P为变负荷的敏感特征值。因此,变负荷和气阀泄漏对示功图及灰度矩阵特征值有耦合影响,且变负荷工况的影响较大,因此首先对压缩机进行负荷的判断会降低其对气阀故障识别的影响,故本文将先进行压缩机负荷的判断,并将负荷值也作为一个特征值再用于气阀故障诊断。
3 基于神经网络及加权证据理论的气阀故障诊断
3.1 BP神经网络
BP神经网络结构简单、自学习能力强、可有效解决非线性函数问题,目前已在多个学科和研究领域中获得广泛应用[14]。BP神经网络的结构如图6所示。一般BP神经网络由多层神经元组成,其中,第一层为输入层,最后一层为输出层,其他各层均为隐含层。目前最常用的为三层神经网络,即包括一个输入层、一个输出层和一个隐含层。理论上已经证明,三层神经网络只要隐含层节点数足够多,就具有模拟任意复杂的非线性映射的能力[15]。

图6 神经网络结构Fig.6 Neural network structure
本文提取示功图的几何特征以及灰度矩阵的统计特征,使用BP神经网络作为分类器,分别将几何特征以及灰度矩阵特征作为BP神经网络的输入,用于负荷预测和故障识别。其中,示功图的形心、面积、形心主惯性矩、卸荷器回撤点及灰度矩阵的σ2、G1、P为负荷识别神经网络的输入值,示功图的x轴形心、膨胀过程斜率k及灰度矩阵的σ2、G1、S作为故障识别神经网络的输入值,将负荷预测值和故障分类作为输出。
3.2 加权证据理论
由于在变负荷工况下,气阀故障和变负荷工况对特征值的影响会发生耦合,故分别通过示功图的几何特征和灰度矩阵特征进行故障识别,并通过加权证据理论对输出进行融合以提高准确度。加权证据理论是基于Dempster-Shafer(D-S)证据理论发展起来的,每组证据的权重系数根据与其他证据体的冲突程度决定[16]。加权证据理论可以根据不同证据体间的冲突程度来分配权值以对各证据体进行融合,提高结果可信度。
将BP神经网络的训练误差En作为不确定度,其计算公式如式(19)所示,则准确度为1-En。

式中tnj、ynj分别表示第j个神经元的期望输出值和实际值。使用BP神经网络的输出计算各证据的基本概率赋值m,如式(20)所示。
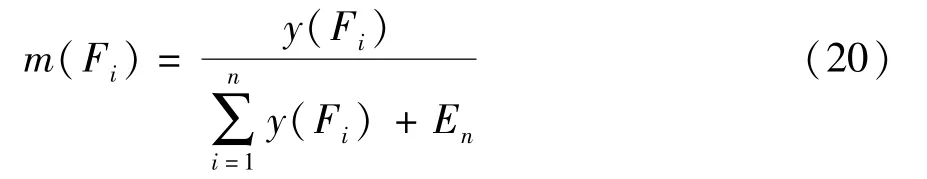
式中,Fi为故障模式;y(Fi)为BP神经网络的输出结果。
3.3 变负荷工况下气阀泄漏实验
采用DW-12/2型往复式压缩机作为实验台,如图7所示。该压缩机为双缸双作用,基本参数见表2。

图7 往复式压缩机实验台Fig.7 Reciprocating compressor test stand

表2 往复式压缩机性能参数Table 2 Performance parameters of the recipr ocating compressor
实验分为4个工况,分别为正常工况以及吸气阀分别有8个、12个和16个泄漏孔的泄漏工况,将这4种工况依次命名为F1、F2、F3、F4,在每种工况下运行一段时间,并进行负荷调节,监测压缩机运行状态,记录压缩机运行时的动态压力。实验中气阀阀片上每个泄漏孔直径d=5 mm。设阀片开孔面积与流通面积比值为阀片开孔面积占比K(即泄漏率),本文实验中4种工况的阀片开孔面积占比如表3所示。

表3 4种工况的泄漏率Table 3 Leakage rate for four working conditions
分别在这4种工况下进行实验,实验过程中调节负荷大小,记录负荷值分别为100%、90%、80%、70%、60%、50%、40%、30%、20%等时的动态压力,采集到有效样本共760个用于示功图分析。本文中BP神经网络训练共使用481个样本,分别为20%、40%、60%、80%、100%负荷工况下的样本数据;测试共使用279个样本,分别为30%、50%、70%、90%负荷工况下的样本数据。
3.4 变负荷工况下气阀故障的识别
对3.3节实验数据进行处理后,提取示功图的几何特征、灰度矩阵统计特征的特征值,并利用BP神经网络对负荷大小进行预测,结果如图8所示。本文中,测试样本共279个,其中调节精度误差小于10%的样本为272个,准确率为97.5%。

图8 负荷预测结果Fig.8 Final calculation results of load prediction
在变负荷工况下,由于负荷变化和泄漏故障的耦合会使得负荷的变化在很大程度上影响泄漏信息,因此首先判断出负荷大小,再利用示功图的几何特征和灰度矩阵统计特征对故障类型进行分类,同时也对初步分类结果进行加权证据融合。预测流程如图9所示,其中神经网络1用于负荷预测,神经网络2使用灰度矩阵特征进行故障分类,神经网络3使用几何特征进行故障分类。最终结果如图10所示。

图9 预测流程图Fig.9 Prediction flow chart
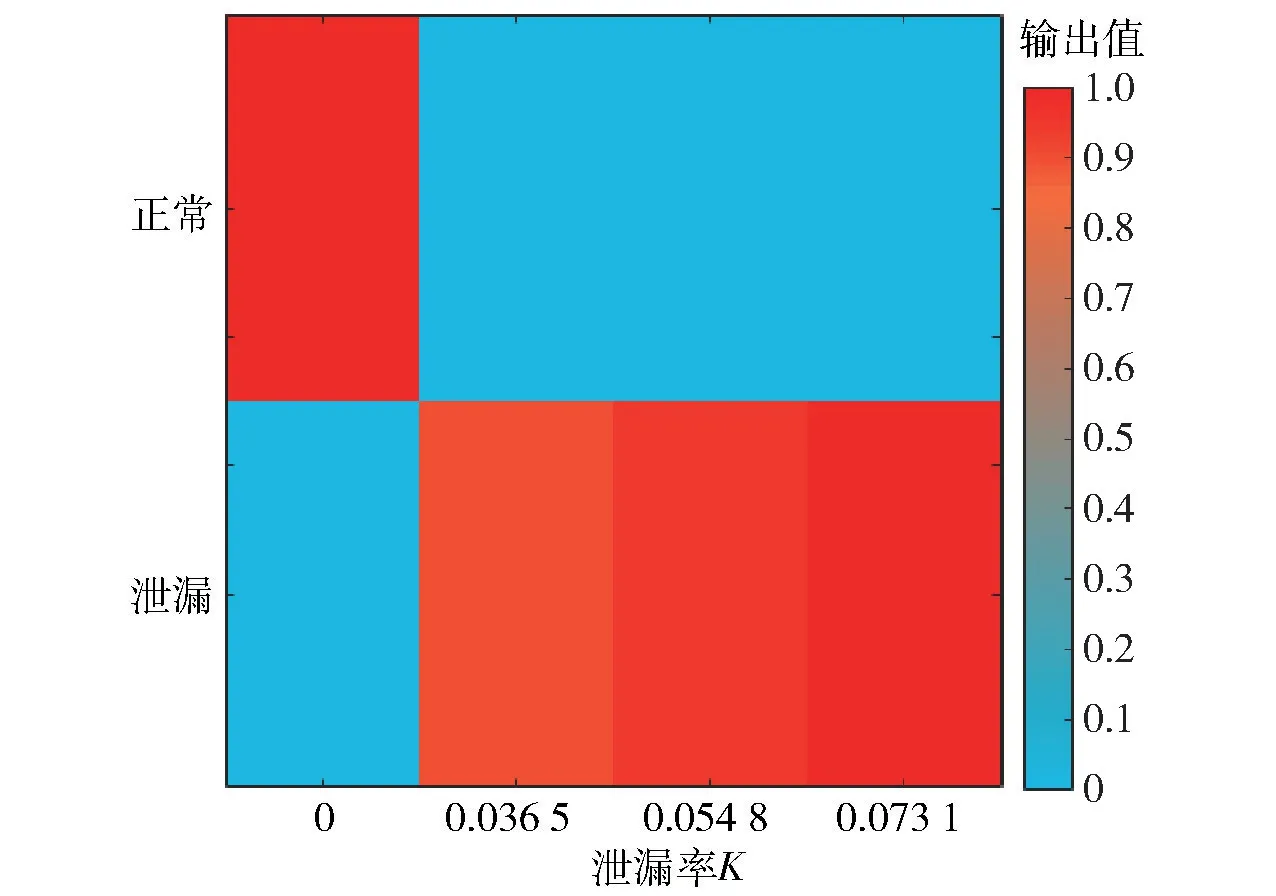
图10 故障预测最终计算结果Fig.10 Final calculation results of fault prediction
从表4和图10中可以看出,将示功图的几何特征与灰度矩阵特征两种信息数据融合后可以明显提高故障识别的准确度,其不确定度接近于0。用不同气阀泄漏工况的共279个测试样本对该方法的准确率进行测试,共识别出268个样本,准确率达到96.1%。
4 结论
本文通过提取示功图的几何特征和灰度矩阵特征,来分析不同特征值对负荷和气阀泄漏的敏感程度,并在压缩机变负荷及气阀泄漏耦合工况下应用加权理论进行故障诊断。研究结果表明神经网络对负荷值和气阀泄漏的识别率较高,且加权理论进一步降低了识别结果的不确定度,对于实际的实验数据,所提方法故障识别的准确率达到96.1%,验证了该方法的可行性。

