一种新型多弹编队控制器设计方法研究

魏诗卉，杨春伟，刘炳琪，王继平，张振林

(1 96901部队, 北京 100096; 2 西北工业大学航天学院, 西安 710072)

0 引言

随着信息化战争的一体化进程不断加快，单枚导弹的作战模式的弊端越来越明显，很多学者致力于研究多弹编队协同作战。多弹编队协同作战，可以提高发现目标的概率，提高导弹的突防能力，提高导弹的毁伤能力，所以很多学者致力于研究编队控制方法。

近年来，无人机的应用日趋广泛。为了提高无人机执行任务的成功率，众多学者提出了多无人机协同完成任务的思想，致力于无人机的编队控制器设计研究。该方法能够在现有无人机功能下提高任务执行成功率。李炳乾等采用领从式无人机编队策略，针对系统中存在气动参数的不确定性以及扰动等问题，采用反步法设计了一种编队控制器。魏扬等在旋转坐标系下建立了无人机编队飞行的数学模型，并采用自适应控制设计了编队保持控制器。张友安等基于人工势场法，给出了无人机编队内部的人工势场函数，并用模型预测控制方法进行优化得到编队控制器。施书成等采用领从式编队策略，借助人工势场法，引入相对速度矢量，给出无人机的引力函数和斥力函数，在速度矢量场作用下，无人机可以实现编队的队形保持。刘小雄等采用混合控制结构对编队飞机进行控制，利用神经网络自适应控制技术使僚机实现良好的跟踪，保持编队之间的相对距离，同时设计三通道神经网络混合PID控制器使得飞行控制系统快速跟踪指令，保持编队队形。林伟利用无人机的目标不同将编队队形控制问题转化为微分博弈问题，针对每个无人机，通过估计其终端状态，利用开环纳什策略进行控制器设计。邵壮等采用虚拟智能体组成编队结构进行控制器设计，采用李雅普诺夫第二稳定性理论加模型预测控制设计了非线性编队控制器。上述无人机编队控制器设计虽不能直接应用于导弹编队控制器设计，但是带来了设计思路。

彭明星等针对反舰导弹协同编队飞行问题，设计了两种基于领弹-从弹法的多导弹编队飞行控制方法。第一种是在惯性系下进行建模，进行编队控制器设计；第二种是根据领弹、从弹及目标的位置关系，设计了编队控制器。马培蓓等利用多智能体系统技术针对编队飞行研究从弹的控制律和实现算法，利用误差的动力学特性设计三维条件下基于从弹的编队控制器。韦常柱等采用最优性理论推导设计了编队飞行控制器，并采用PI最优控制理论，设计了鲁棒性较强的最优编队控制器。张磊等采用微分几何理论建立从弹跟踪误差和相对速度误差，利用黎卡提方程求解的方法设计了从弹的编队跟踪控制器。杜阳等考虑多弹编队碰撞冲突问题，设计了基于局部模型预测的编队防碰控制器。谷逸宇基于领弹从弹模型，针对机动目标，利用编队误差的动力学特性，设计了多弹编队飞行的导引律。

现有文献多集中于领弹-从弹相对系和惯性系下的编队控制器设计。文中将领弹看作虚拟目标，在现有弹目相对运动方程的基础上进行控制器设计，简化了在领弹-从弹相对系下编队控制器的建模过程。首先，将领弹看作虚拟目标，建立了三维空间中的弹目相对运动方程；紧接着，将弹目距离、视线倾角和视线偏角看作状态变量，采用滑模控制进行编队控制器设计；最后，经过仿真，验证了文中方法的可行性和有效性。

1 编队控制器设计基础

编队控制器的设计思路是将领弹看作虚拟目标，在从弹和领弹的视线系下进行编队控制器设计，所以首先建立弹目相对运动方程。下面给出从弹的三维攻击几何如图1所示。

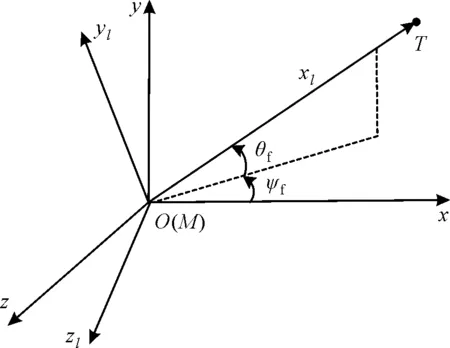
图1 从弹三维攻击几何

如图1所示，代表从弹；代表目标；代表惯性坐标系；代表弹目视线坐标系；为视线倾角；为视线偏角。

导弹与目标相对运动方程为:

(1)

2 编队控制器模型

编队控制器设计思路来源于多弹协同攻击。视线系下编队形式如图2所示。

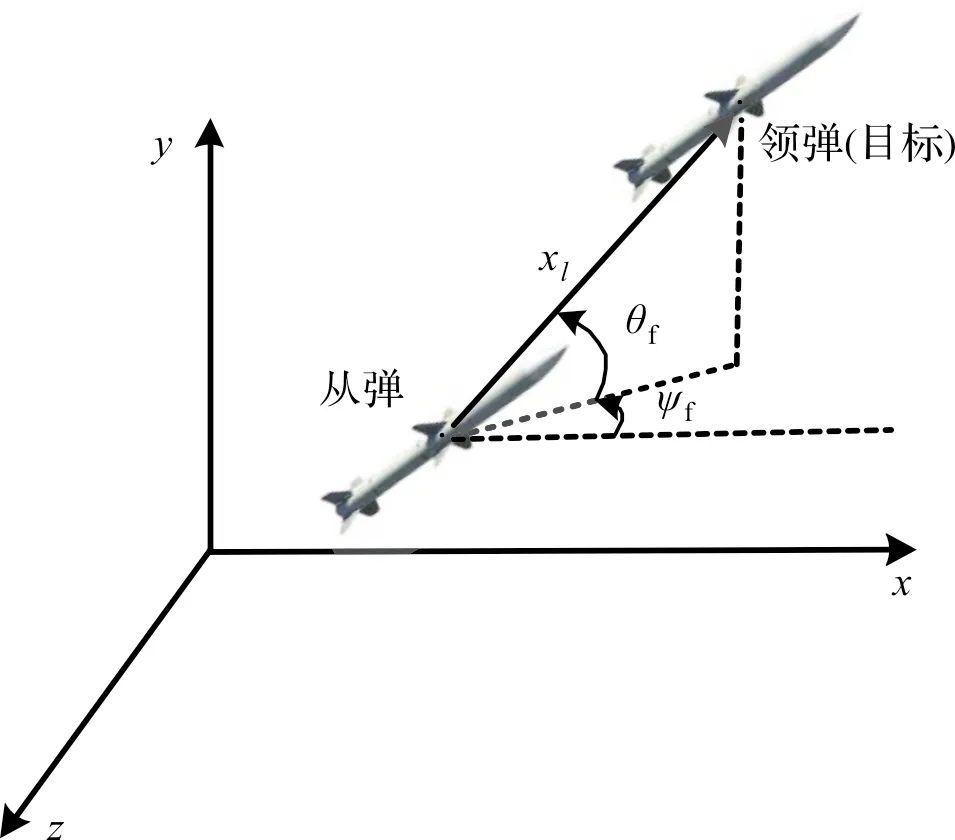
图2 视线系下编队形式示意图

如图2所示，我们将领弹视作目标，两枚从弹视为攻击导弹，编队目标是使两枚从弹与领弹保持一定的相对位置，形成编队队形，并保持下去。

在视线系下，需要对弹目距离、视线倾角和视线偏角进行控制，才可以保证两枚从弹与领弹保持期望相对位置。

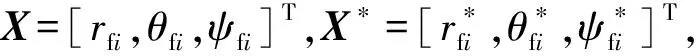
令误差=-，可以得到误差的具体表达式：

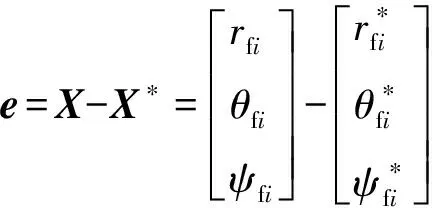
(2)

假设给定的期望值均为常值，所以对式(2)求导，得到误差的一阶导数为：

(3)

式(2)和式(3)中的未知变量为：

(4)

式中：f=-f;f=-f;f=-f。

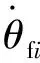
(5)

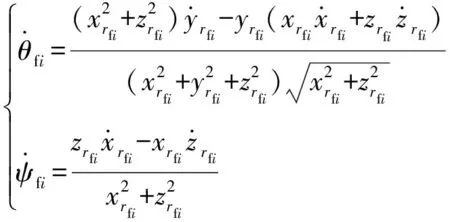
(6)

对式(6)进行求导，得到误差的二阶导数的过程较为麻烦，为了减小计算量，由式(1)可得弹目距离、视线倾角和视线偏角的二阶导数。

(7)

即编队跟踪位置误差的二阶导数为：

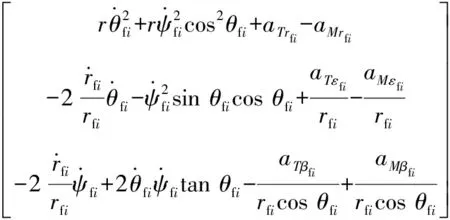
(8)

令

(9)

式中：

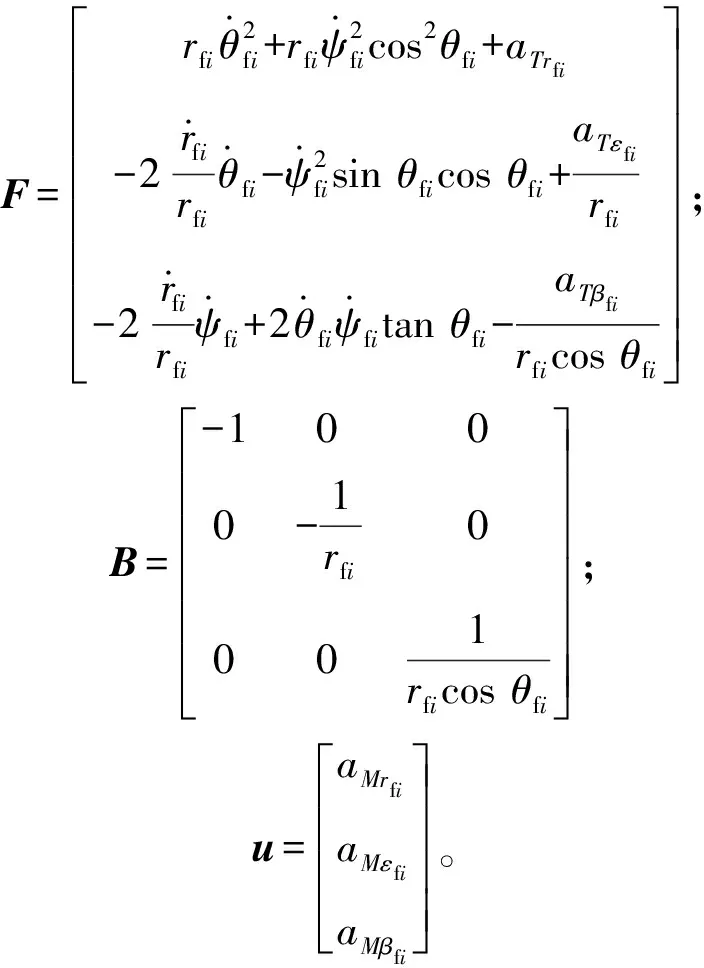
其中，为控制量。

因此，控制系统可以写作:

(10)

3 控制器设计

采用滑模变结构控制对编队控制系统进行控制器设计。

选用非奇异终端滑模面：

=sig()+

(11)

式中:=diag(,,)，>0,∈1,2,3;∈(1,2);对于向量=[]，有sig()=[||sign() ||sign() ||sign()]。

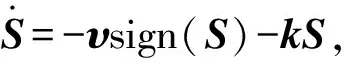
对式(11)求导，得

(12)

式中，=1,2,3。结合滑模面，可得:

(13)

得控制量的表达式为：

(14)

4 稳定性分析

(15)

为了证明式(14)为渐近稳定，采用引理进行说明。

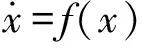
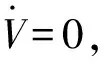
5 仿真分析

采用3枚导弹进行编队仿真，领弹按照自己的轨迹飞行，两枚从弹在视线系下进行控制，实现期望的编队队形并保持下去。编队控制器中的参数值设置为=diag(12,12,12)，=diag(1,11,08)，=diag(182,182,182)，=15，仿真步长=0.01 s，领弹的初始位置为(0 m,10 000 m,0 m)，初始速度为1 000 m/s，视线系下的过载提前给定：=sin(0.3)m/s，=5sin(0.3)m/s，=0 m/s。两枚从弹的具体初始信息如表1所示。

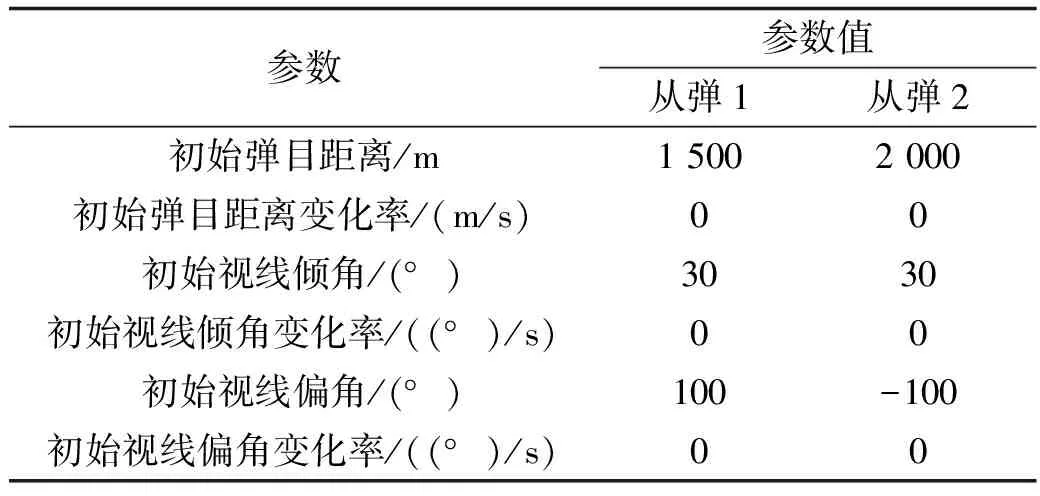
表1 从弹的初始条件

按上述仿真条件进行仿真，可以得到领弹和两枚从弹的仿真如图3～图8所示，编队误差如表2所示。

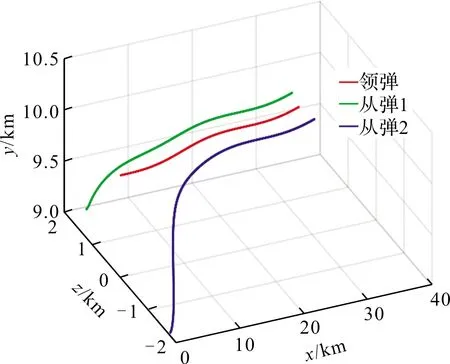
图3 编队轨迹曲线

图4 两枚从弹的弹目距离与期望弹目距离的误差曲线

图5 两枚从弹的视线倾角与期望视线倾角的误差曲线

图6 两枚从弹的视线偏角与期望视线偏角的误差曲线

图7 从弹1过载曲线

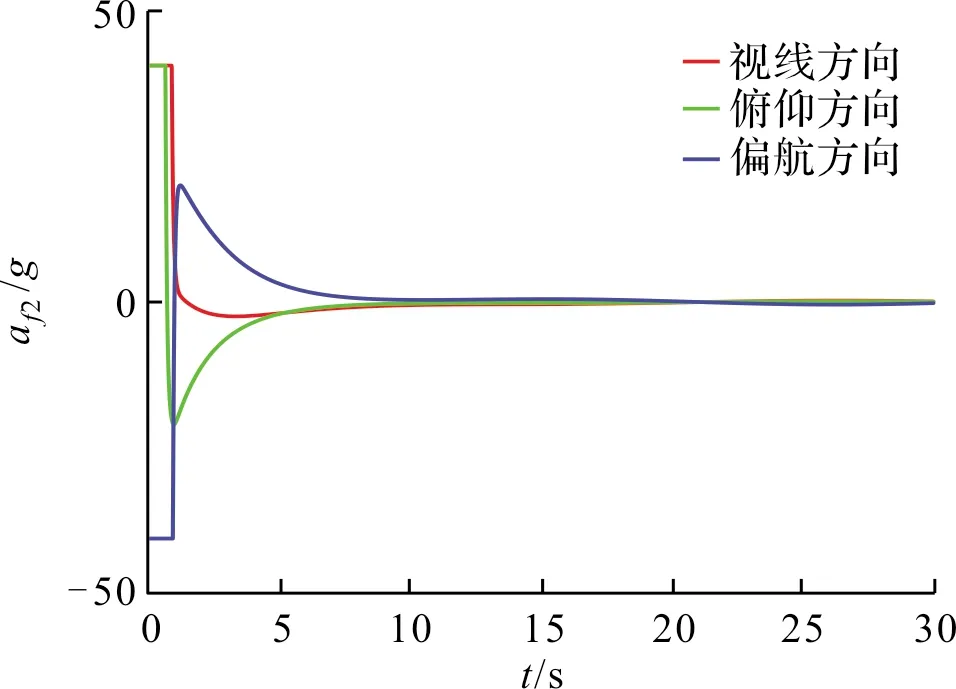
图8 从弹2过载曲线

如图3所示为一枚领弹和两枚从弹的三维编队轨迹曲线，观察该图，可以发现两枚从弹在初始阶段进行调整，最终能够达到我们预先设定的编队队形，并保持下去。

如图4～图6分别为两枚从弹的弹目距离、视线倾角和视线偏角与期望值的误差，可以在图中看出，两枚从弹能够在弹目距离、视线倾角和视线偏角这3个状态变量上实现很好的跟踪。反映到表2中，弹目剩余距离的最大误差为0.05 m，视线倾角和视线偏角的误差在0.005°之内，这对于编队来说，效果非常好。

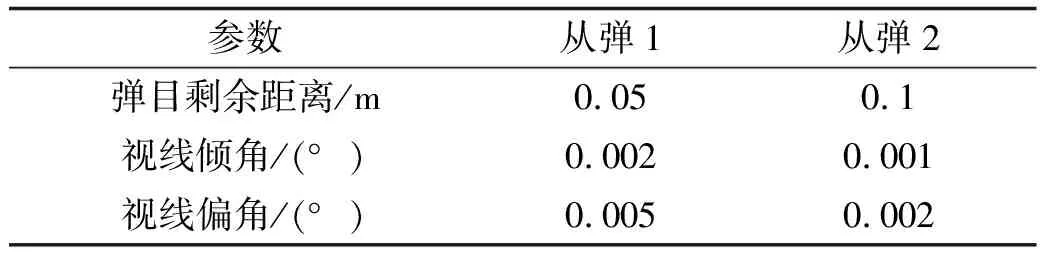
表2 两枚从弹的编队误差

图7～图8分别为两枚从弹的过载曲线，可以看出，两枚从弹的过载曲线较为平滑，对执行机构的损伤较小，更符合实际应用。另外，根据仿真结果可以看出，设计的编队控制器的收敛时间约为10 s，相比现有文献，收敛时间略有提高。

6 结论

重点研究了视线系下的多弹编队控制器设计方法，主要思想是将领弹当作目标，然后采用从弹攻击领弹的思想，使弹目距离、视线倾角和视线偏角能够达到给定的期望值。首先，推导出了视线系下的弹目相对运动方程，为后续的编队控制器设计提供研究基础；然后，将弹目距离、视线倾角和视线偏角视为状态变量，求出这3个变量的实际值与期望值的偏差，偏差的一阶导数和二阶导数，然后利用滑模控制求得编队控制器；最后，进行了仿真，验证了设计的编队控制器能够实现并保持编队，而且效果较好。