反辐射导弹的角度型制导方法研究

唐道光，张 意，刘叙含，王 乔，李 涛，杨 丹

(1 中北大学电气与控制工程学院，太原 030051; 2 西安现代控制技术研究所, 西安 710065;3 西南计算机有限责任公司技术中心，重庆 400060)

0 引言

在战术导弹自动导引、无人飞行器进场着陆、航天器交汇对接以及行星探测器自主着陆等方面，制导律起到了不可替代的作用。根据不同的导引目的、不同的交汇场景，已衍生出形式多样的制导律种类，如比例导引、增强型比例导引、偏置比例导引、带终端角度约束的制导律、时间协同制导律等。这些制导律既可能是基于线性模型，也可能是基于非线性模型的。总体而言，根据所采用的制导信息类型，可分为角速率型制导律和角度型制导律两类。前者需要视线角速率信息，而后者所用的是角度相关信息。尤其对视线角速率信息获取困难或精度不理想的情况，如低成本制导弹药、捷联制导弹药、雷达反辐射导弹，准确的视线角速率信号获取没有硬件支持或获取代价较高，这种情况下应用角度制导律就很有意义。

基于不同的终端约束，各类制导律的研究已经较为广泛和深入。Zarchan, Garnell等在经典著作中对比例导引、弹道成型等进行了深度分析；Wang等在多约束最优制导律的解析研究方面取得了一定成果；Ryoo, Lee等在多约束最优制导方向开展了系统的研究，提出了角度最优制导、多项式制导等一系列显著成果。此外，协同制导、三维制导、多约束优化等也是近些年的热点研究课题。

通过建立相对于终端弹目连线的导弹运动方程，得到以角度形式表示的比例导引，并推导了基于传统比例导引的积分型比例导引、速度追踪。基于不同的动力学模型和制导误差，对比分析了其性能差别。

1 反辐射导弹的制导需求

空射反辐射导弹通常划分为四代，分别以AGM-45“百舌鸟”、AGM-78“标准”、AGM-88“哈姆”、AGM-88E等为典型代表，制导方式历经被动雷达、宽频带被动雷达、惯性+被动雷达、卫星/惯性+主被动复合等。当末制导采用被动雷达制导时，被动雷达导引头往往并不能直接测得弹目视线角速率，直接的测量值是目标相对被动雷达导引头的误差角，误差角与导弹惯导的弹体姿态角或速度矢量角组合后，才可能得到可用的弹目视线角。相对而言，处理得到的弹目视线角速率信号噪声会比较大，运用比例导引的效果并不总是很好。研究表明，利用弹目视线角信号，采用角度型制导的方式，对降低信号噪声引起的脱靶量是有益的。

2 无动力学滞后的最优制导律

2.1 数学模型

对地面固定目标，导弹和目标的几何关系如图1所示，LOS表示当前弹目视线(line of sight);(,)表示导弹的位置;(,)表示目标的位置;表示导弹速度;表示导弹加速度指令;为弹道倾角；为弹目相对速度。根据图1的几何关系，为简化起见，定义:

图1 弹目运动几何关系图

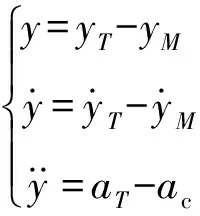
(1)

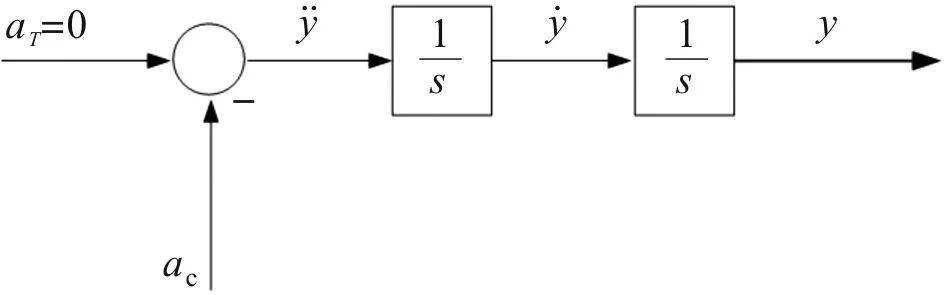
图2 弹目运动几何关系框图

将式(1)写成系统状态方程的形式:

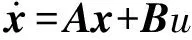
(2)

2.2 基于最优控制理论的制导律

将目标函数定义为：

(3)

根据式(2)，将终端约束表示成矩阵形式:

()=

(4)

若仅约束()==0，则矩阵、为:

(5)

根据最优控制理论，上述最优问题的解可表示为:

()=[()-]

(6)

式中:

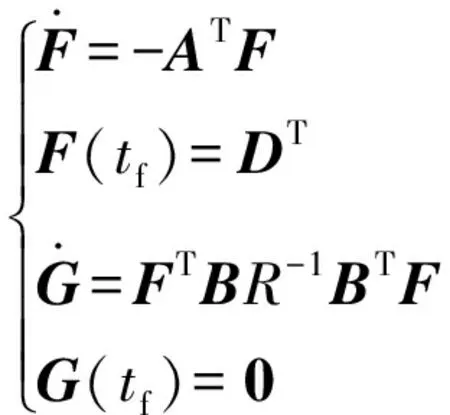
(7)

将矩阵、带入式(6)、式(7)，则最优制导律的表达式为：

(8)

其中，定义=+3为导航比。

3 比例导引、积分比例导引、速度追踪的角度表示

3.1 比例导引的两种表达形式

基于小角度假设，认为弹目视线角为小角。根据图1的几何关系，有

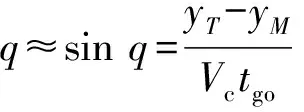
(9)

微分后得到:

(10)

将式(9)、式(10)代入式(8)中，得到：

(11)

(12)

将式(9)、式(12)代入式(8)，得到：

(13)

令

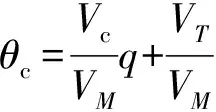
(14)

则得到:

(15)

若目标为固定的，则

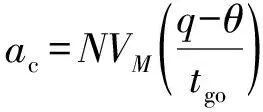
(16)

式(11)、式(15)和式(16)为比例导引的两种不同形式，其中后者为比例导引的角度表示形式。

3.2 积分型比例导引和速度追踪的角度表示

不考虑弹体动力学，则=，其中为弹体的加速度响应。根据弹体动力学，有

(17)

联立式(11)和式(17)，两边同时积分，得到:

(18)

若仅针对固定目标，则=1,式(18)可简化后写成加速度的形式:

=[(-)+(-)]

(19)

若暂不考虑积分初值，且取1，则上述积分比例导引退化为速度追踪，如式(20)所示：

=(-)

(20)

对比式(16)的比例导引和式(20)的速度追踪，可以发现，比例导引相对于速度追踪引入了时变的导航增益。

为简化起见，假设目标为固定的，不考虑积分初值，则上述3种基于角度的制导律表达式如表1所示。

表1 3种基于角度的制导律

4 基于高阶动力学的积分比例导引、速度追踪制导模型

不考虑积分比例导引的积分初值，假设系统具有初始方向误差输入，则系统的通用化制导框图如图3所示。

图3 通用化制导框图

其中:表示制导时间；导航增益可能为或1，分别表示积分比例导引和速度追踪。图3通过等价变换后，得到图4。

图4 等价变换后的模型

根据图4，假设高阶动力学为1(+1)，根据动力学阶数的不同将分母展开，如表2所示。由此可见，不管如何取值，这种模型能够保证一阶环节的时间常数为。

表2 高阶动力学模型分母展开

图4可具体表示为图5。

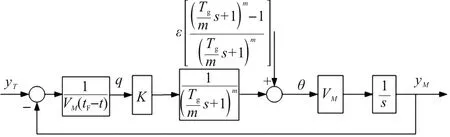
图5 速度追踪高阶动力学制导模型

比例导引的制导模型研究较多，此处不再赘述。观察可以发现，假设制导动力学完全一致，则比例导引和积分比例导引的区别在于，积分比例导引需考虑积分初值和的影响；在比例导引的方向误差输入为，而积分比例导引或速度追踪的方向误差输入为:

(21)

5 积分比例导引、速度追踪与比例导引的脱靶量对比研究

5.1 积分比例导引和比例导引在初始方向误差作用下的脱靶量对比分析

为简化分析，仅考虑目标固定的情况，即=。根据第4节的动力学模型，假设比例导引也引入同样的高阶制导动力学1(+1)，初始指向误差为误差输入。在不同动力学阶数下的脱靶量仿真结果如图6所示。由此可见，对同样的高阶动力学系统，在上述的初始方向误差输入条件下，比例导引(proportion navigation, PN)和积分比例导引(integral proportion navigation, IPN)的脱靶量没有明显区别。

图6 积分比例导引和比例导引脱靶量对比

5.2 积分初值对积分比例导引的脱靶量影响

对积分比例导引，引入积初值和，则制导框图如图7所示。

图7 IPN 制导系统

图8、图9的仿真结果表明，对不同的动力学阶数，只要导航系数≥2且无量刚末导时间>10，则IPN系统的积分初值引起的脱靶量都会趋近于0。

图8 积分初值θ0作用下的积分比例导引脱靶量

图9 积分初值q0作用下的积分比例导引脱靶量

5.3 速度追踪和比例导引在初始方向误差作用下的脱靶量对比分析

速度追踪的制导框图如图10所示，仿真结果如图11、图12所示。

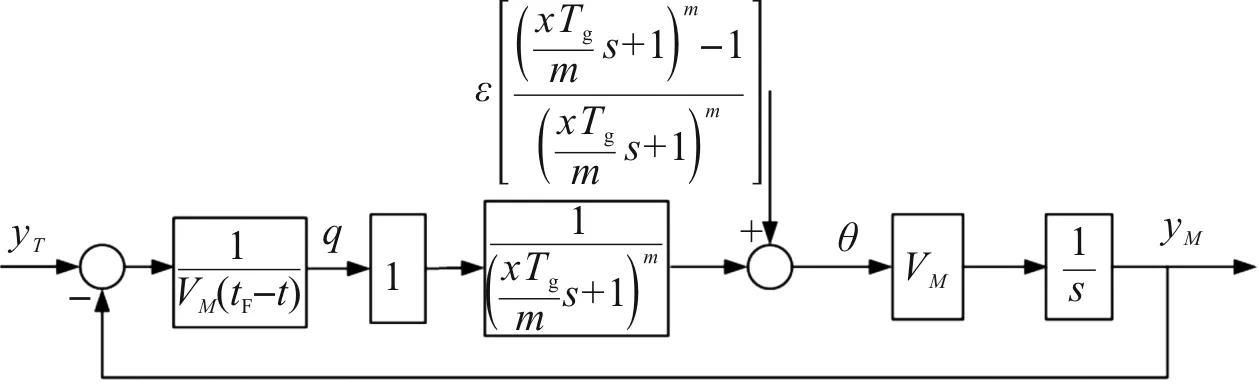
图10 速度追踪制导模型

图11 动力学阶数对初始方向误差作用下的速度追踪制导系统脱靶量影响(从1阶到5阶)

图12 速度追踪和比例导引脱靶量对比

速度追踪和比例导引的仿真结果表明，在实际制导系统中，速度追踪随的增大有较大的脱靶距离，这表明在同一导弹特征控制点，速度矢量驾驶仪比过载驾驶仪慢，因此在实际制导系统中，速度追踪可能有较大的脱靶量。

6 结论

在最优比例导引的基础上，基于弹目视线角和弹道倾角，推导了比例导引、积分比例导引和速度追踪的角度型表达式。针对积分比例导引和速度追踪的高阶动力学系统，建立了具有初始指向误差的制导模型。通过脱靶量的仿真对比分析，说明了比例导引、积分比例导引和速度追踪的制导性能差异。从制导律结构角度分析，传统的比例导引与过载驾驶仪相匹配；而积分比例导引、速度追踪与速度矢量驾驶仪相匹配。对同样的制导动力学和导航系数，初始方向误差引起的积分比例导引和比例导引脱靶量基本一致。在初始方向误差作用下，要达到相同的脱靶量，速度追踪要求的末导时间大于比例导引。此外，虽然角度型制导律更适用于攻击固定或慢速移动目标，但工程上对视线角量测精度要求较高，弹载测量硬件的量测精度对角度型制导律影响较大。

比例导引法的优点是可以通过恰当的参数组合实现全向攻击且弹道较平直，缺点是命中时的需用法向过载受命中点的导弹速度和攻击方向影响较大。早期战术导弹受硬件水平限制，视线角速度难以直接测量，因而多采用积分比例导引。速度追踪技术上易实现，但是绕后攻击导致弹道弯曲，对导弹机动性提出较高要求。在选择导引方法时，需综合考虑导弹的飞行性能、作战空域、技术实施、战术使用、制导设备与精度等方面的需求。