变步长采集的外弹道试验历史数据处理方法

魏雪梅，黄建忠，刘保炜，韦 卓，李晓哲

(中国兵器工业试验测试研究院，陕西 华阴 714200)

0 引言

在远程制导火箭外弹道试验数据抢救过程中，由于当时试验测试未要求或者设备失效等，导致大量外弹道试验速度和加速度数据的缺失，需要通过对历史保存的外弹道试验位置数据分析处理，支撑数据关联展示和数据挖掘等。传统采用GJB2234A—2014进行外弹道试验数据处理，该标准给出了等步长时间间隔下，速度分量和加速度分量的处理方法。在实际数据处理应用中，对于等步长间隔数据采集的测试设备，可以直接采用该标准计算得到外弹道速度和加速度。然而，对于变步长间隔数据采集的测试设备，则无法使用该标准进行速度和加速度分量的计算。文中针对这一问题，对GJB2234A—2014中的计算速度分量、加速度分量公式进行了分析，给出一定误差范围内不等步长速度、加速度计算新公式，基于新公式采用Matlab建模并计算验证。

1 数据收集方法

在远程制导火箭试验时，一般通过光电经纬仪和雷达跟踪，得到目标运动过程的外弹道参数。对于光电经纬仪设备以及雷达采集的外弹道试验数据，通常可直接采用GJB2234A—2014中的算式，根据设备所测外弹道位置参数、、计算，可得到目标沿、、方向的运动速度和加速度；然而，对于相控阵雷达采集的数据，由于其外弹道位置参数、、并未按照等时间间隔采样，其数据时间序列的随机性强，导致了速度和加速度分量计算的困难。

2 速度、加速度求解函数

2.1 函数定义

GJB2234A—2014“光电经纬仪事后数据处理方法”中定义速度分量和加速度分量的计算公式为：

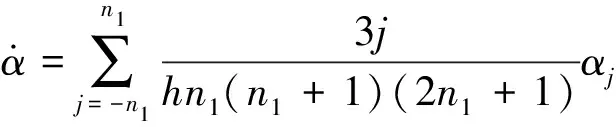
(1)

(2)

式中：为速度平滑半点数；为加速度平滑半点数；为数据采样时间间隔；为弹道位置参数、、。

2.2 数学模型应用

将光电经纬仪或雷达采集的外弹道位置数据代入式(1)和式(2)，通常在平滑点处前后共选取7个点做平滑处理，以某次试验中雷达的测试结果为例，弹道位置参数、、由雷达测试所得，如图1所示。

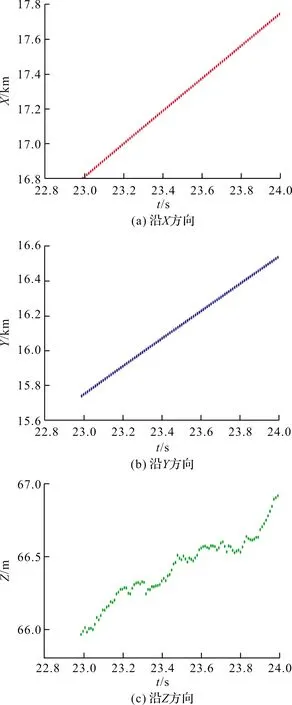
图1 WEIBEL雷达测试的外弹道位移

将位移数据代入式(1)得到沿、、方向的弹道速度曲线，如图2所示。

图2 计算的外弹道速度曲线图

将相关参数代入式(2)得到沿、、方向的弹道加速度曲线，如图3所示。

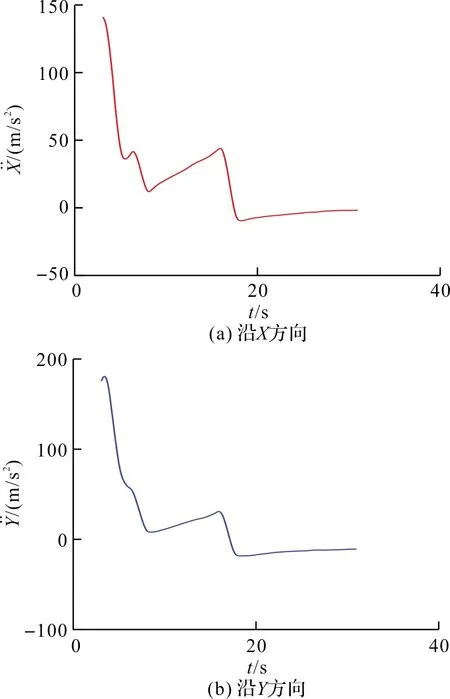
图3 计算的外弹道加速度曲线图

3 改进的速度、加速度求解函数

3.1 变步长采集的函数定义

将式(1)中的采样间隔变为，可得：

(3)

同理，对式(2)中的变为，可得：

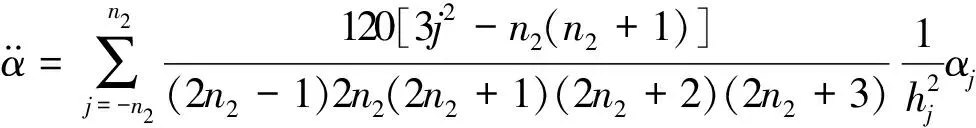
(4)

3.2 生成不等间隔时间序列

以相控阵雷达跟踪某远程制导火箭试验为例，已知雷达所测的外弹道位置参数为()、()、()，其时间序列为(,,,…,)，其中，为采样最大个数。不等时间间隔序列可表示为：

=+1-

(5)

式中：=1,2,3,…,-1。

3.3 循环迭代

以射程()为例，记全弹道过程中，射程序列为(),(),(),…,()，假设以某点为例，求解该点处的平滑曲线，则取该点处前后各个点做数据平滑处理，并将式(5)代入式(3)，可得()点处平滑速度为：

(6)

将式(5)代入式(4)，取该点处前后各个点做数据平滑处理，可得()点处平滑加速度为：

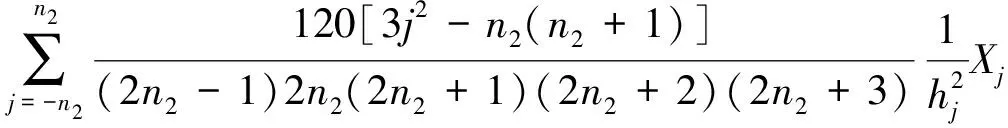
(7)

4 数据分析处理

以某型制导火箭弹外弹道试验数据为例，在本次试验中测试所得弹道飞行过程中沿、、三个方向的位移，如图4所示。

图4 相控阵雷达测试的某型外弹道位移

将位移矩阵代入式(6)，得到平滑的合成速度如图5所示。

图5 计算的速度曲线

已知相控阵雷达所测的速度文件，将计算结果与之进行比较，结果如图6所示。

由图6可见：相对误差基本保持在5%以下，最小误差可达0.047%，最大误差为5.52%。则证明该算式的正确性，使用该方法计算变步长采样的外弹道试验数据速度分量是可行的。

图6 速度比较及相对误差

5 结束语

在实际的弹道跟踪试验测试数据处理中，测试数据出现采样间隔不规律的现象时有发生。文中通过改进GJB2234A—2014的速度、加速度求解算式，采用时间序列代替原有常数时间间隔，试验测试数据平滑处理更加方便，既可用于等步长采样测试数据处理，又能够应用于变步长采样测试数据处理。然而，该算法在平滑过程中并未考虑平滑点两侧步长相差过大的问题，后续还需要进一步修正以减小平滑误差。