基于卡尔曼滤波器的激光驾束制导导弹制导方法研究

吴光辉，方东洋，陈意芬，许新鹏，张 迪

(上海机电工程研究所，上海 201109)

0 引言

激光驾束制导体制导弹以其制导精度高，抗干扰能力强，弹上结构简单，成本较低等优点，在防空导弹、反坦克导弹等领域具有广泛的应用。比较有代表性的激光驾束制导防空导弹有瑞典的RBS70导弹和英国的“吹管”导弹，激光驾束反坦克导弹有南非的“猎豹”反坦克导弹和俄罗斯的“短号”反坦克导弹和“漩涡”空地导弹。

激光驾束制导导弹根据与激光驾束中心的位置偏差形成制导指令，王狂飙等将线偏差乘以比例系数后经过一个超前滞后校正网络得到制导指令。王婷等针对驾束制导导弹,运用超扭曲二阶滑模控制理论,提出了一种一体化制导控制系统设计方法。通过选择线偏差、线偏差导数、过载及角速率作为状态变量,建立了描述制导控制回路的一体化状态方程组，将状态量进行组合设计滑模面，从而达到控制线偏差的目的。李召等为解决激光驾束制导体制下，导弹攻击运动目标存在滞后的问题，采用卡尔曼滤波器对瞄准线的角速率进行估计，并生成一个与瞄准线转动角速度有关的附加补偿加速度指令，提高了驾束制导的位置控制精度。蒋军等针对激光驾束制导体制，推导了驾束制导各个环节误差到脱靶量误差的传递函数，并通过蒙特卡洛仿真对推导结果的合理性进行了验证。Ratnoo采用三点法导引导弹对抗正弦机动目标，其中对位置误差采用超前校正方法，同时对目标运动引起的加速度进行补偿，取得了较好的制导精度。虽然目标引起的加速度补偿为理论值，但是为三点法导引提高制导精度提供了思路。为了增大驾束制导导弹的有效射程，周军等提出将低成本红外导引头与激光驾束相结合的复合制导方案。在近距离采用驾束制导，超出驾束制导距离后切换为红外导引头制导，增大导弹有效射程。张翔等对激光驾束导弹的半实物仿真环境搭建进行详细的描述，采用二轴转台模拟激光驾束场的角运动。赵辉等对存在侧风条件下的驾束制导导弹控制方法进行研究，通过采用卡尔曼滤波器对导弹侧滑角进行实时估计，并在驾驶仪中进行前馈校正，提高了驾束制导导弹抗侧风能力。

由于导弹只能测量相对于驾束中心的位置偏差，当应用PID控制器时，差分求解位置偏差的变化率会引入较大的噪声。采用最速微分器对位置偏差进行跟踪提取位置偏差的变化率，以位置偏差、位置偏差变化率、目标运动引起的加速度为状态量，根据常值加速度运动模型，采用卡尔曼滤波器对系统状态进行滤波。数值仿真结果表明，基于卡尔曼滤波器的PID控制器控制效果较好，当引入目标引起的加速度补偿后，制导精度得到了提高。

1 相对运动方程

导弹与目标的相对运动关系如图1所示，以地面制导站为原点，在导航坐标系下，先后旋转视线方位角和视线高低角，得到视线坐标系。与目标质心重合，指向目标，为制导站到导弹的距离。导弹加速度在视线系的投影为

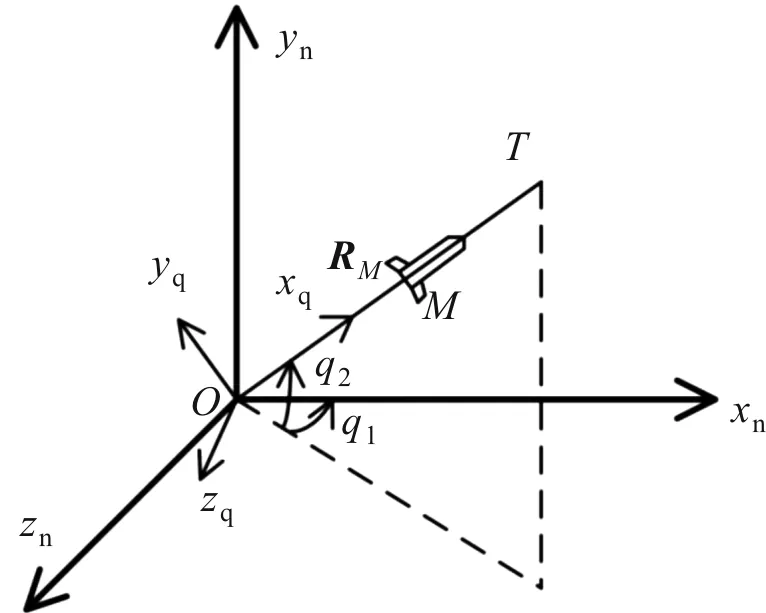
图1 相对运动关系示意图

q，目标加速度在视线系的投影为q。视线坐标系相对于导航坐标系的转动角速度在视线系的投影为，视线系角速度与欧拉角速度之间的关系为:

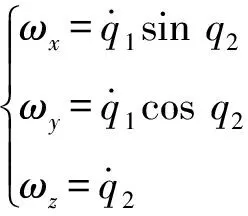
(1)

其中，，，是视线角速度的三轴分量。

导弹位置在视线系的投影为q，对位置矢量采用绝对导数和相对导数的关系进行推导，得到导弹速度在视线系的投影为:

(2)

对速度矢量q采用绝对导数和相对导数的关系进行推导，得到导弹加速度在视线系的投影为:

(3)

进行展开可以得到三维空间下弹目相对运动方程为：

(4)

其中：，，是导弹位置q的三轴分量；x，y，z为加速度q的三轴分量。

以纵向平面为例对方程进行简化，得到：

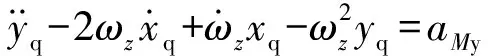
(5)

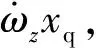
2 最速跟踪微分器

对导弹的相对位置进行控制时，需要引入相对位置的变化率作为阻尼信号。由于相对位置的测量信号易受到噪声污染，采用差分算法会使噪声放大。韩京清提出利用二阶最速开关系统构造出非线性跟踪微分器概念，最速跟踪微分器在对输入信号进行跟踪滤波的同时，输出跟踪信号的近似微分信号。因此采用最速微分器对测量的相对位置进行跟踪，得到相对位置的变化率。

建立最速微分器跟踪模型：

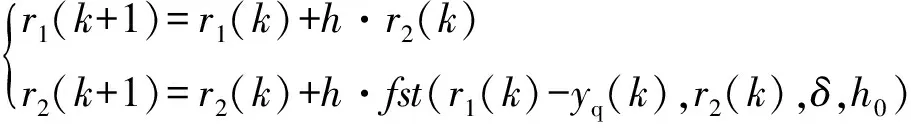
(6)

其中：()，(+1)分别为测量位置信息在时刻和(+1)时刻的滤波值；()，(+1)分别为位置变化速率在时刻和(+1)时刻的滤波值；，分别为采样步长和滤波因子，滤波因子取采样步长的整数倍；()为时刻测量得到的位置信息；为决定跟踪快慢的参数；(·)函数为最速控制综合函数。

(7)

(8)

以()和()为测量信息，采用卡尔曼滤波器对目标引起的加速度状态进行估计，同时对()和()进行滤波，将经过卡尔曼滤波后的信号应用到位置控制的PID控制器中，使控制指令更加平滑。

3 卡尔曼滤波器

从式(5)可以看出，由目标运动所引起的需用加速度与视线角速度和视线角加速度相关。视线角速度与视线角加速度可以在地面测量后通过无线信息传递到弹上计算机，但是这样会增加成本以及降低抗干扰能力。通过直接测量的位置信息和跟踪微分器得到的位置速率信息对目标加速度进行滤波处理和目标加速度指令补偿，可以减小对硬件平台的依赖。

将目标运动引起的加速度统一表示为，重写式(5)为：

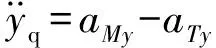
(9)

采用常值加速度模型对目标运动引起的加速度进行建模，得到系统的状态方程为：

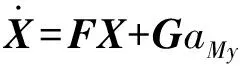
(10)

其中，状态量、系数和表示为：

(11)

对状态方程进行离散化，取转移矩阵的一阶表达形式：

-1=+T

(12)

其中为采样周期。给出离散状态下卡尔曼滤波的基本方程为：

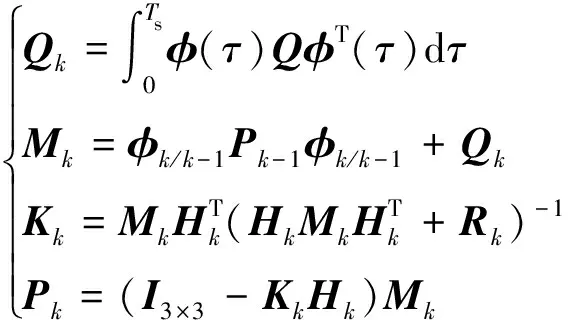
(13)

其中：为预测协方差矩阵；为卡尔曼滤波增益；为量测矩阵；为系统噪声矩阵；为测量噪声矩阵；为状态误差协方差矩阵。

状态方程的预测值为：

-1=-1-1+y,-1

(14)

校正值为：

=-1+(--1)

(15)

其中，=[(),()]为测量值。根据以上卡尔曼滤波器对相对运动状态进行滤波，将滤波后的状态应用到位置PID控制器中。

4 数值仿真

如图2所示，采用位置PID控制器对激光驾束导弹进行位置控制，保证导弹始终位于激光驾束场中心，位置控制指令置为零。激光驾束测量位置为，形成负反馈信号，经过PID控制器得到制导指令，PID信号与目标加速度补偿形成制导指令c。假设驾驶仪为二阶环节，自然频率为20 rad/s，阻尼为0.7。设计控制器时，以相位裕度大于50°设计PID控制参数，，分别为8，5，5。

图2 PID位置控制器结构框图

得到制导指令表达式为：

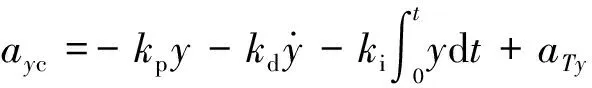
(16)

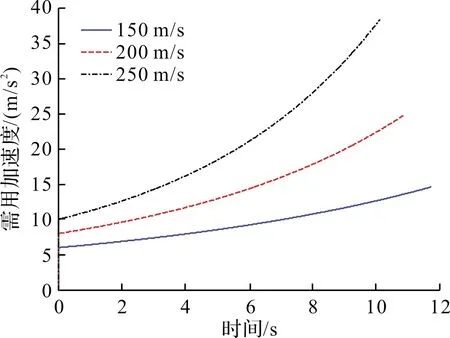
图3 不同目标速度需用加速度曲线

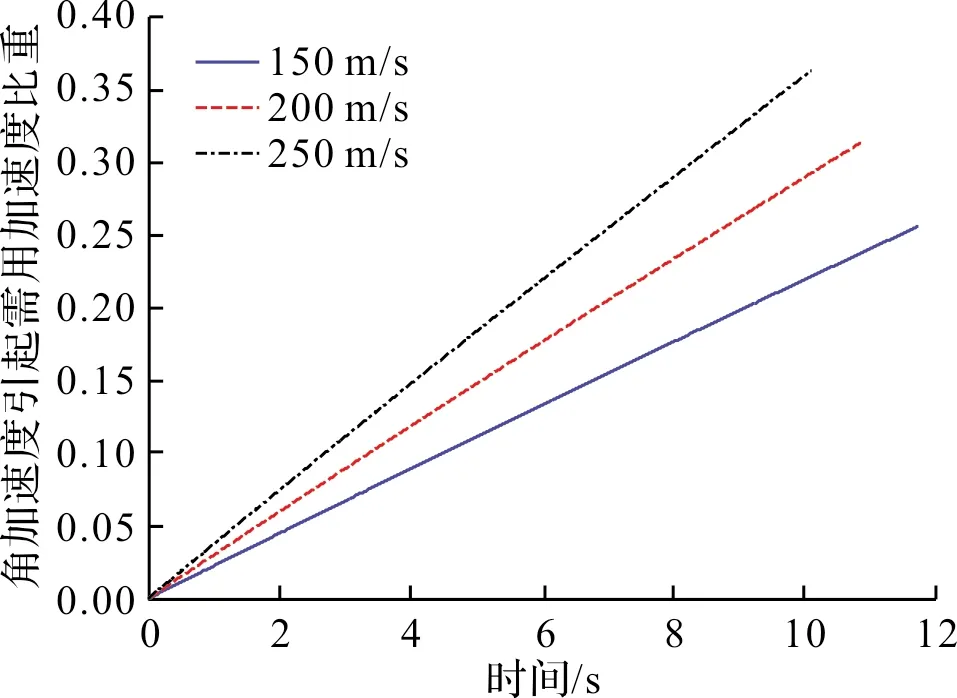
图4 不同目标速度角加速度引起的需用加速度分量

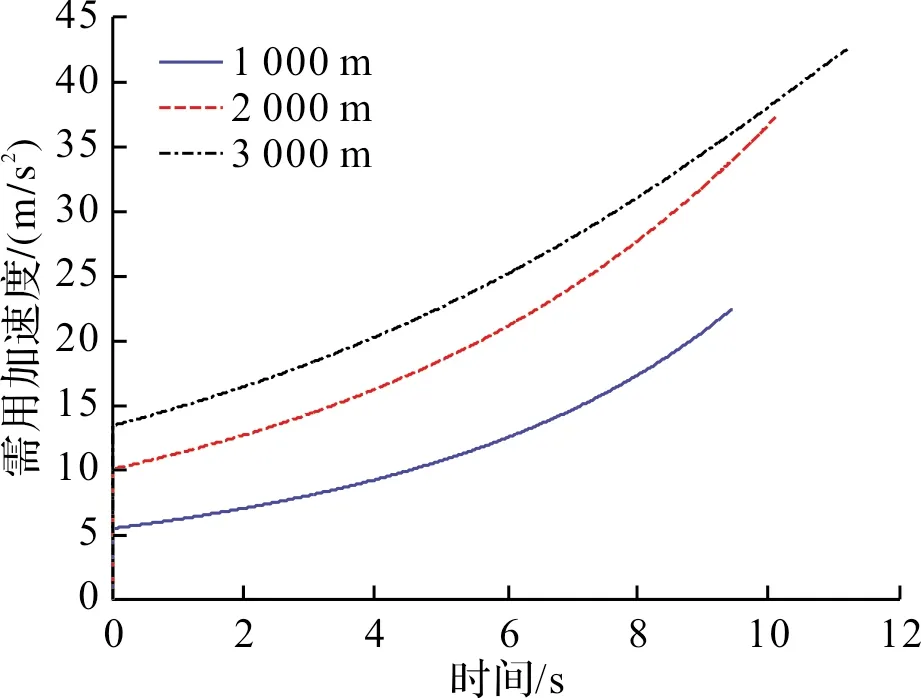
图5 不同目标高度需用加速度曲线

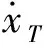
从图6可以看出，采用PID控制器加目标加速度补偿方法时，末端脱靶量为0.32 m，仅采用PID控制器时，末端脱靶量为1.02 m，采用目标加速度补偿方法时，控制效果较好。从图7可以看出，对跟踪微分器提取的微分信号进行滤波，得到卡尔曼滤波后的位置速率曲线，滤波效果比较平滑。从图8可以看出，采用常值加速度模型时，对目标加速度的滤波曲线比较平滑，趋势跟踪效果较好，由于目标运动模型存在偏差，滤波后的目标加速度与真实目标加速度存在常值差值。由于采用了PID控制器，目标加速度滤波值存在一定的偏差时，也能取得较好的制导效果。

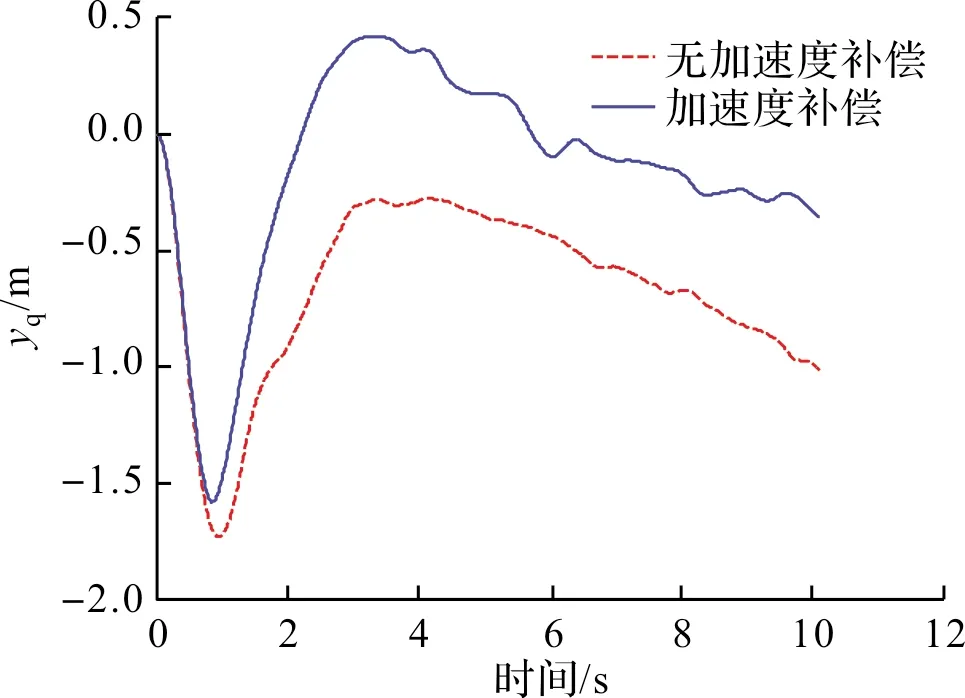
图6 线偏差响应曲线

图7 线偏差速率响应曲线

图8 目标加速度滤波响应曲线

5 结论

提出了一种基于卡尔曼滤波器的PID位置控制方法，针对激光驾束制导导弹取得了较好的控制效果。通过对相对运动关系进行推导，得到需用加速度表达式。目标需用加速度由两部分组成，其中与视线角速度有关的部分占主要因素。采用激光驾束体制的三点法导引，目标高度越高，速度越快，需用加速度越大。因此，采用激光驾束制导体制的防空武器主要针对低空近程防空。在不增加硬件的情况下，采用卡尔曼滤波器对目标引起的加速度进行估计，通过对位置和位置速率进行滤波，使制导指令更加平稳。采用三点法导引时，目标加速度处于不断增大的趋势，因此下一步工作中，研究在保证指令平稳的同时使得目标加速度的估计精度得到提高。