基于学生经验的小学数学概念教学对策

【摘要】本文论述小学数学概念教学应基于学生已有的隐性经验、生活经验、点状经验等，提出教学时应采取激活学生的隐性经验让学生经历概念形成的过程、沟通全面经验理解概念的本质、挖掘生活经验内化概念、整合点状经验拓展概念外延等策略。

【关键词】小学数学 数学概念 学生经验

【中图分类号】G62 【文献标识码】A

【文章编号】0450-9889（2022）16-0056-03

概念教学是小学数学教学的重要内容，也是学生深入学习数学知识的基础。当前小学数学概念教学中存在着直接给学生呈现概念，让学生记概念、背概念、用概念的现象，导致学生对数学概念的理解不深、把握不准。那么，教师怎样引入数学概念、如何设计概念课教学，才能让学生经历数学概念的形成过程，深刻理解数学概念的内涵与外延呢？笔者认为，教师作为课堂教学的组织者与实施者，需要精心设计数学概念的问题背景和学习情境，将数学概念教学与学生的隐性经验、生活经验、点状经验等有机结合起来，才能避免学生在学习数学概念时感觉突兀。一般而言，小学生的经验有隐性经验、生活经验、点状经验等。教师可以利用学生已有的经验，通过类比、辨析等方法開展数学概念教学，将抽象概念形象化、复杂问题简单化，才能有利于促进学生对数学概念本质的理解。

一、激活隐性经验，经历概念形成的过程

隐性经验是指学生内化于心，在缺乏契机的情况下无法直接运用的经验。学生在学习新的数学概念之前，都具有一定的隐性经验。教师要善于激活学生的隐性经验，促进学生认知的正向迁移，助力学生完成数学概念的探究。在数学概念教学中，教师可以将数学概念与学生的直接经验结合起来，激活学生的隐性经验，帮助学生厘清思路，提炼数学概念的本质。

以人教版数学五年级下册“真分数和假分数”教学为例。本课要求学生认识真分数和假分数，了解它们之间的联系和区别，掌握真分数和假分数的概念及其特征。要达成教学目标，教师可以结合学生已有的知识和等分经验（分数的意义）展开教学，设计“分饼”活动，引导学生将已有的知识和新知识进行类比，让学生在类比活动中掌握真分数和假分数的概念。

第一，激活学生的等分经验。教师给学生出示一块圆形饼干，请学生思考：如果将这块圆形饼干分给4个小朋友，怎样分才能使每个小朋友得到的饼干一样多？学生利用等分经验，将一块圆形饼干平均分成4份，4个小朋友得到的饼干就一样多。“分饼”活动激活了学生已有的等分经验，将等分经验与分数建立起了联系。

第二，关联隐性的分数经验。学生利用“等分法”分饼干之后，教师再请学生说一说每个小朋友分得多少饼干？分得的每一份，用除法算式如何表示？用分数如何表示？完整的计算过程是什么？学生回忆分数的意义，明确：一个圆形饼干等分成4份，每一份就是1÷4，用分数表示就是[14];两份就是1÷4×2，用分数表示就是[24]，代表2个[14];3份就是1÷4×3，用分数表示就是[34]，代表3个[14];4份就是1÷4×4，用分数表示就是[44]，代表4个[14]，也就是一个圆形饼干。在这个教学环节，教师引导学生说一说分饼干和计算的过程，利用学生已有的生活经验和隐性经验（分数的意义）展开教学，自然过渡到真分数和假分数的概念教学。

第三，提炼概念的本质。在此基础上，教师请学生思考：如果将这个圆形饼干分成5份该怎么分，分成6份怎么分、分成7份怎么分……分成n份，又怎么分？用分数如何表示？学生结合分数的意义分析得出：4份就是4个[14]，用分数表示就是[14];5份就是5个[14]，用分数表示就是[54];6份就是6个[14]，用分数表示就是[64];7份就是7个[14]，用分数表示就是[74]……如果分成n份，就是n个[14]，用分数表示就是[n4]。

将一个圆形饼干平均分成4份用分数如何表示，扩展到分成5份、6份、7份，用分数如何表示，目的是激活学生的隐性经验，让学生经历假分数概念的形成过程，认同假分数产生和存在的合理性，明确假分数的概念，即分子比分母大或者分子和分母相等的分数就是假分数。

第四，区别真分数和假分数。经过比较和分析，学生发现，真分数和假分数都是一个分数单位，它们的区别在于，真分数的分子小于分母，假分数的分子大于或者等于分母，并且真分数小于1，假分数等于或者大于1。

以上四个教学环节，教师基于学生已有的等分经验、分数经验等隐性经验，通过开展“分饼干”活动，引导学生将除法和分数建立起联系，让学生经历假分数概念的形成过程，在此基础上提炼真分数和假分数的概念，掌握真分数和假分数的特征。

二、沟通全面经验，正确理解概念的本质

小学生学习数学概念，容易受到片面经验的影响，分析问题时往往以偏概全，“想当然”地解决问题，造成思维受阻，出现混淆概念的现象。教学中，教师要认真对待学生的片面经验，运用辨析策略，引导学生发现自己的错误，寻找出错的原因，沟通全面经验，正确理解数学概念的本质，完善数学认知结构。

以人教版数学三年级上册“分数的初步认识”为例，大部分学生有这样一个片面的认知，认为在分东西的时候一定要平均分、等分。这样的片面经验不利于学生学习分数的概念，会影响学生对分数概念的正确认知和对分数概念的意义建构。因此，教学时教师可以创设“分东西”活动情境，引导学生辨析等分和不等分两种情形。

首先，教师创设“分东西”活动情境：有8根胡萝卜，分给2只小白兔和2只小灰兔，要让小白兔比小灰兔多吃4根胡萝卜，怎么分？学生动手操作，列出算式，很快得出答案：小白兔吃6根胡萝卜，小灰兔吃2根胡萝卜。接着，教师设计“寻找彩带的二分之一”学习活动，出示一根彩带，要求学生找出彩带的二分之一。学生知道将一根完整的彩带当作单位“1”，将它平均分成两份，每一份就是二分之一。此时教师提问学生：“二分之一是什么意思？”学生思考后认为：分数二分之一实际上是建立在“平均分”的基础上，它不仅表示分的过程，还表示分得的结果。在这两个学习活动中，学生通过“分胡萝卜”认识到分东西可以有多有少，并非一定要平均分，通过“找出彩带的二分之一”认识到分数[12]是基于“平均分”得到的。

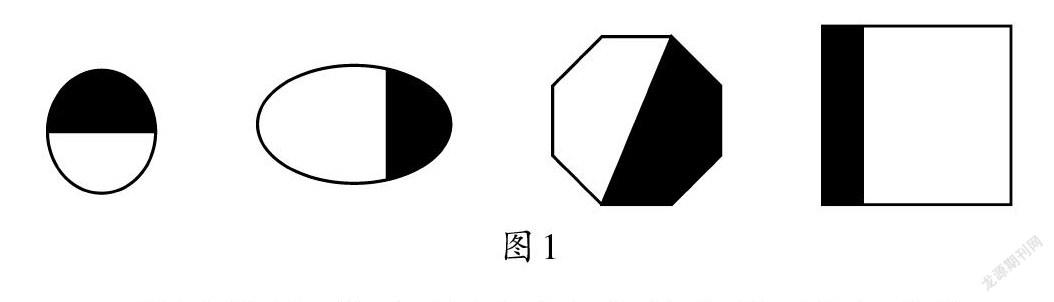
其次，辨析分数的“等分”本质。为了让学生对“等分”具有更深入的理解，教师可以给学生设计折纸涂色活动。首先给学生发放一张正方形白纸，让学生将白纸对折：对折一次后打开，纸被折成两个部分;对折两次后打开，纸被折成4个部分，同时在折痕处画上虚线。然后请学生思考会产生哪些分数？通过3次对折，学生意识到每一次对折都是将单位“1”等分成2份，两次对折就是等分成4份，3次对折就是等分成8份，由此可知，对应的每一份分别是分数[12]，[14]，[18]。最后，教师给学生出示图1，请学生判断图中涂色的部分能不能用分数[12]表示？

经过辨析，学生理解了分数的本质：只有平均分才能用分数来表示。教师让学生辨析问题，打破了片面经验“分东西就要等分”的思维定式，使学生从固化的思维经验中走出来，形成了“分东西可以等分，也可以不等分的”全面经验，确保学生全面把握数学概念。

三、挖掘生活经验，内化概念的内涵

生活经验是指学生在学习过程中将数学概念与生活常识进行同化或顺应，促进对数学概念本质的理解。小学生具有一定的生活经验，这些生活经验能够促进学生对数学概念的理解。教师要善于发掘学生的生活经验，引导学生将生活经验上升为策略经验，使其成为学生内化数学概念的抓手。

以教学人教版数学五年级上册“解方程”为例。为帮助学生掌握方程的概念，教师可以通过“猜数”游戏挖掘学生的生活经验，促使学生内化方程这一概念，具体做法如下。

首先，挖掘生活经验，建立联系。开始“猜数字”游戏之前，教师先请学生在心里默念一个数字，然后将这个数字翻一倍后加上20，求出得数。学生说出结果后，教师再说出学生心里默念的那个数字，学生判断教师说出的数字是否正确。最后，学生猜一猜教师是如何猜出这个数字的？小学生喜欢玩游戏，教师利用“猜数字”游戏诱发学生的生活经验，使学生积极参与到猜数字游戏中。学生猜测数字的过程，就是一个将未知数和已知数建立联系的过程，这正是学习方程的关键，也是学生将生活经验与方程建立联系的契机。

其次，运用生活经验，厘清思路。教师向学生提出问题：“小明心里想着一个数字，这个数字翻倍后加上20，得数为60。请你猜一猜小明心里想的这个数字是多少？你是怎么猜出来的？”学生经过思考和分析，认为可以使用“逆推法”计算，先用60-20=40，再用40÷2=20，20就是小明心里想的数字。学生运用生活中常见的逆向推理经验进行计算，很快得出结果，解题思路清晰，无形中将已知数和未知数建立起了联系，也就是建立了方程模型。

最后，拓展生活经验，自主解题。学生学会了运用逆向推理的经验解决问题，教师可以趁机给学生出示练习题：4x+6=30，4x-20=60，同时告知学生x代表教师心里想的数字，请学生结合已有的经验说一说如何解答题目。从“猜数字”游戏到具体的算式解答，学生的解题思路会越来越清晰。经过计算，得出4x+6=30中的x=6，4x-20=60中的x=20。实际上，学生解答题目的过程，也就是解方程的过程，这是对逆向推理经验的拓展和运用，无形中内化了方程的概念。

教学数学概念时，教师要善于挖掘学生已有的生活经验，引导学生利用生活经验尝试解决数学问题，学会将生活经验上升为策略经验，使其成为解决问题的方法，更好地内化数学概念。

四、整合点状经验，拓展概念的外延

点状经验是指基于不同的知识点而生发出来的经验，它具有不稳固的特点，偏于表象化，不能成为普适性的经验。很多时候，学生对数学概念的认识和理解往往是感性的，而这感性的认识就是点状经验。教学数学概念时，教师要让学生稳固点状经验，基于点状经验展开思考和反思，引导学生梳理已有的知识经验，整合点状经验，使学生形成理性化的思维表达和抽象思维，加深对数学概念的理解，适时拓展数学概念的外延，完善知识结构。

学习人教版数学四年级下册“三角形的内角和”之后，学生可以获得三角形内角和的推导经验，如测量法、剪拼法、折叠法、作辅助线法等。为了稳固学生的点状经验，教师请学生自主探索多边形的内角和，并思考问题：可以用三角形的内角和推导多边形的内角和吗？学生利用三角形的内角和推导方法，结合已有的经验，思考后认为可以将多边形分割成若干个三角形，再将分割出来的三角形的内角和相加。那么，如何分割多边形呢？学生观察发现，可以将多边形的一个顶点作为出发点，把这个点与各顶点连线，就可以将多边形分割成若干个三角形，这样可以确保分割的有序性和科学性。利用这个方法，学生发现规律：四边形可以分割成两个三角形，五边形可以分割为3个三角形，六边形可以分割为4个三角形，而多边形的内角和就是分割成的三角形的个数乘以180°。

学生利用三角形内角和的学习经验探究四边形、五边形、六边形的内角和，并将这些点状经验进行联系与整合，理解了三角形的内角和这一概念，并将其与多边形的内角和进行关联，从而完成了三角形内角和这一概念的拓展学习。

在实际教学中，隐性经验、生活经验、点状经验并没有明显的界限，各种学习经验往往是互相交融和促进的。在小学数学概念教学中，教师要以学生为主体，引导学生弄清楚数学概念的来龙去脉，经历数学概念形成的过程，深入理解数学概念的本质及其特征，适当进行拓展和训练，以提高數学概念教学实效。

参考文献

[1]张文文.以学生经验为基础的小学数学教学策略探究[J].新智慧，2021（25）：65-66.

[2]陆佳.基于学生生活经验的小学数学教学思考[J].数学大世界，2020（10）：92.

[3]杨汉英.基于学生经验培养的小学数学课堂教学分析[J].数学大世界，2019（8）：98-99.

[4]吴琴.学生经验及其在小学数学教学中的利用研究[D].武汉：华中师范大学，2019.

[5]杨德乌.基于生活经验的小学数学教学策略实践与研究[J].新校园，2015（12）：81.

[6]林炳良.基于学生经验展开教学：小学数学“时分认识”教学案例与思考[J].内蒙古教育，2013（10）：52-53.

作者简介：李小燕，广西浦北人，一级教师，研究方向为小学数学教学。

（责编 欧孔群）