怎样求解立体几何最值问题

田利剑

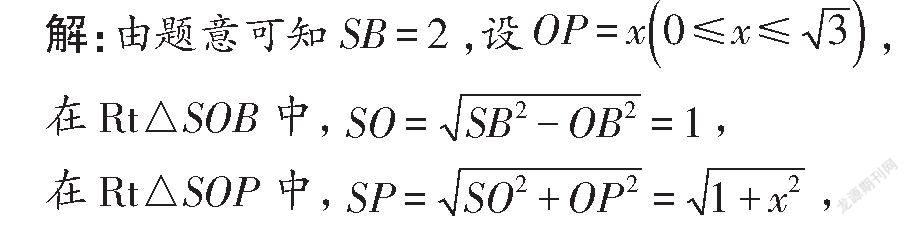
立体几何中的最值问题具有较强的综合性，对同学们的空间想象能力和运算能力有较高的要求.常见的立体几何最值问题有线段最值问题、面积最值问题以及体积最值问题.下面结合实例来谈一谈这三类立体几何最值问题的解法.

一、线段最值问题

立体几何中的线段最值问题比较常见，通常要求某条线段的最大值或最小值.求解立体几何中的线段最值问题，需先将该线段视为平面几何图形的一条边，然后根据平面几何图形的性质，如平行四边形的性质、等腰三角形的性质、直角三角形的性质，确定该条边的最大、小值，或根据勾股定理、正余弦定理求得该线段的表达式，运用函数的性质、基本不等式求得最值.

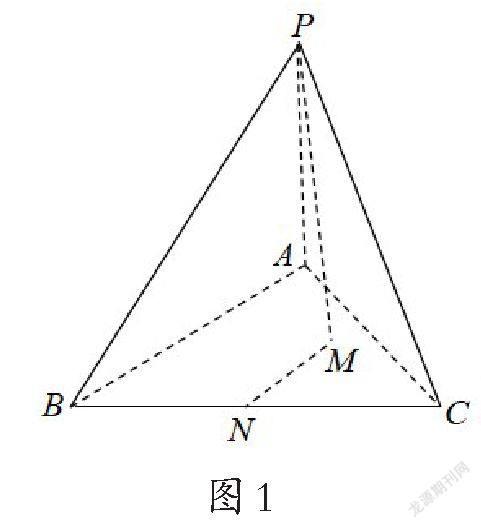
例1.如图1，在三棱锥P-ABC中，PA⊥底面ABC，△ABC为等边三角形，PA=AB=2，点N为BC的中点.若点M为△ABC内一点，且∠MPA=30°，则MN的最小值为________.

分析：由于点A为定点，点M为动点，且∠MPA=30°，故AM为定值，则可推断出点M的轨迹为一段圆弧. 将求的最值问题转化為圆上的点到圆心的距离问题，根据圆的性质即可求出最值.

解：如图2，连接AM，AN，

∵PA⊥底面ABC，∴PA⊥AM，

∴点M的轨迹在以A为圆心，AM为半径的圆弧，

∵△ABC为等边三角形，AB=2，点N为BC的中点，

将点M视为圆弧上的一点，将MN看作圆内的一条线段，便可将立体几何中的线段问题转化为平面内的距离问题，利用平面几何图形的性质来解题.

二、面积最值问题

立体几何中的面积最值问题往往和截面有关，这类问题的求解思路为：①将已知的线段、角及其关系转化到截面上;②利用勾股定理、正余弦定理，求得在截面上的各条线段、角的大小;③根据平面几何图形的面积公式求得几何图形面积的表达式;④利用函数的性质、基本不等式等求得最值

分析：首先作出截面△AMN，如图3所示，然后对未知变量做出假设，设OP=x，再根据三角形的面积公式求出截面的面积，利用二次函数的性质即可求得最值.

连接OM，如图3，

因此，当x=1时，△SMN的面积最大，其值为2.

三、体积最值问题

立体几何中的体积最值问题较为复杂.要求得最值，需先根据题意确定变化的量，如动点、动直线、动平面，然后设出相应的参数，将其视为自变量，求出几何体体积的表达式，再根据函数的性质、基本不等式求得最值.还可以通过分析几何图形，找到几何体的体积取得最值时的情形，根据简单几何体的体积公式求得最值.

例3.如图4所示，在三棱锥P-ABC中，BC⊥平面PAC，PA⊥AB，PA=AB=4，且E为PB的中点，AF⊥PC于F.当AC变化时，三棱锥P-AEF体积的最大值是________.

解：在三棱锥P-ABC中，由BC⊥平面PAC，得BC⊥AC，

∵AB=4，∴AC+BC=AB=16，

易知△PAF∽△PCA，

设AC=a，0

令m=a+16，易知16<m<32，

由于AC为动直线，故三棱锥P-AEF体积也随之发生变化.需首先设出参数，根据已知条件和三棱锥的体积公式得到三棱锥P-AEF的表达式，然后根据相似三角形的性质求出S的表达式，再根据二次函数的性质求得最值.

通过上述分析不难发现，大部分的立体几何最值问题都需借助平面几何知识来求解.因此求解立体几何最值问题时，可根据题意和几何图形的特点，将点、线、面及其关系转化到同一个平面内，然后利用平面几何知识列出关系式，再根据函数的性质、基本不等式求得最值.