点云自适应精简算法在钢轨廓形三维结构光检测中的应用
税 文,王培俊,屈仁飞,赵 瑞,赖宸宇,罗 鑫
(西南交通大学机械工程学院,成都 610031)
近年来,我国高铁在路网建设、科技创新、产业化能力等方面取得了巨大的成就。铁路提速的同时,对安全性的要求也日益严格,钢轨廓形参数和磨耗参数的精准检测成为铁路日常维护的重要工作之一[1]。
目前,我国的轨道检测方式仍以传统的手工检测为主,检测参数单一、检测精度与效率较低,检测结果不便于数字化管理,同时检测劳动强度大,难以满足轨道检测多参数、高精度、高效率的要求。结构光三维成像技术是一种非接触式的轮廓点云获取技术[2],它能够快速、精确、完整地采集钢轨表面轮廓点云,单幅点云采集幅面宽,能够同时检测多种钢轨参数,极大地提升了钢轨检测的精度与效率。
三维结构光扫描幅面宽以及鱼尾板、扣件、连接螺栓等铁路现场轨道连接件的存在,导致现场扫描获得的原始钢轨点云除目标点云外,还存在大量噪声点与离群点。这些杂点的存在极大地影响后续点云处理的精度与效率,因此必须对原始点云进行精简滤波。目前常见的点云滤波算法有直通滤波、体素滤波、统计滤波、条件滤波和半径滤波等[3]。郭进[4]提出了基于密度k-means和改进双边滤波相结合的点云去噪算法。柳赟[5]采用基于主成分分析与曲面拟合对点云进行去噪,曲面拟合的精度对滤波的结果影响较大。周煜[6]在不借助任何拟合曲面的前提下,提出一种基于递归分层聚类的线扫描点云采样算法。针对含边界的噪声点云,李国俊[7]提出了一种基于Delaunay三角化的噪声点云非均匀采样算法。肖俊[8]提出通过密度聚类的方法去除原始点云中的离群点,但是主要依据最小聚类点数进行去噪,当离群点云和目标点云的聚类规模一致时,该方法的滤波效果不佳。除此之外,还有基于曲率[9]、法矢[10-11]等点云特征的滤波算法,但是计算较为复杂。
针对铁路现场点云中杂点的多样性与不确定性,综合利用钢轨点云的几何特征与分布特征对其滤波,有效地去除噪声点与离群点,同时自适应精简点云,为后续的点云处理奠定基础。
1 点距自适应及点云摆正的算法实现
1.1 点距自适应的实现
点云精简中采用的常规算法如密度聚类算法、平面分割算法与体素滤波中的相关参数均需人为设定,降低了检测效率。为了提升算法的鲁棒性,排除人为因素的影响,满足不同分辨率下点云的处理需求,本文实现了相关参数的设定与点距自适应。在点云均匀分布的情况下,计算每一个点和距它最近点之间的距离作为该点的点距,然后对所有点的点距求均值作为整个点云的点距,如图1(a)所示。铁路现场扫描的点云分布并不均匀,如图1(b)所示,如果仍采用最近点距作为整个点云点距的计算基础,将会导致点距计算结果偏小。
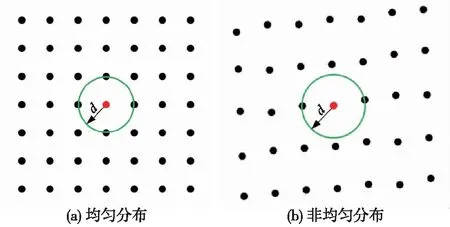
图1 点云分布
为了保证点距计算更加符合实际,取每个点和距它最近的4个点之间的距离均值作为该点的点距,保证每个点四周的临近点均参与点距计算,然后以该点距作为基础计算整个点云的点距。首先对整个点云建立k-d搜索树,该数据结构能够对每个点的邻近点进行快速搜索,查询出最近的4个点后,求出查询点与它们之间的距离均值,计算公式如下
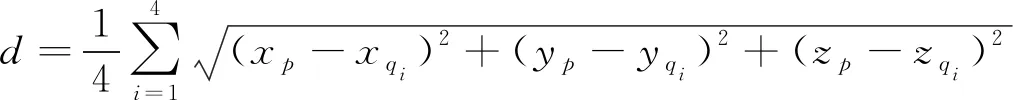
(1)
式中,p为查询点;qi(i=1,2,3,4)为p的4个最邻近点。
然后对所有点的平均点距求均值,得到整个点云的点距,计算如下
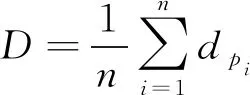
(2)
1.2 点云摆正
1.2.1 密度聚类算法
具有噪声的基于密度的聚类(Density-Based Spatial Clustering of Applications with Noise,简称DBSCAN)方法是一种经典的密度聚类算法[12],该算法基于一组邻域参数(ε,MinPts)来描述样本分布的紧密程度,其中ε描述了某一样本的邻域距离阈值,MinPts描述了某一样本的距离为ε的邻域中样本个数的阈值[13]。DBSCAN算法将簇定义为密度相连的样本的最大集合,能够将密度足够高的区域划分为簇,不需要提前给定簇的数目,并可在有噪声的空间数据集中发现任意形状的簇,同时对样本的输入顺序不敏感。
如图2所示,设MinPts=4,红色的点在ε邻域内的点数均≥MinPts,称为核心点。图中用绿色箭头连起来的核心点组成了密度可达的样本序列。
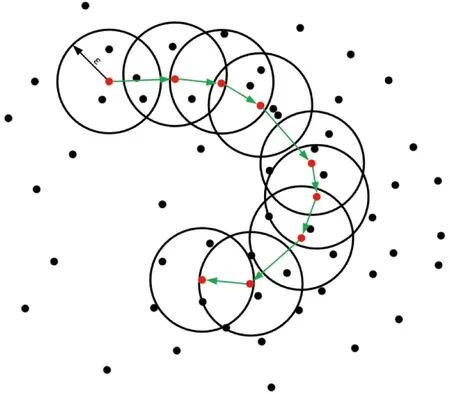
图2 密度聚类示意
1.2.2 平面分割算法
随机采样一致性(Random Sample Consensus,简称RANSAC)算法是一种用于数据处理的经典方法[14],将该算法运用于平面分割中,其基本思想是从一组给定的包含噪声点和外点的点云中,估计出点云的平面模型参数[15]。该算法主要有τ和max两个输入参数,τ是判断某个点是否为内点的误差阈值,该参数对平面点云数据的波动性具有较大影响;max是平面迭代的最大次数,作为终止条件,该参数直接影响RANSAN算法参与模型参数的检验次数,从而影响算法的效率。
1.2.3 钢轨点云摆正算法设计
铁路现场扫描钢轨点云时,三维结构光扫描仪拍摄角度的不同以及是否使用全局坐标点进行拼接等,都会影响原始点云的空间位姿。为了使原始点云的空间位姿明晰,需要将其按照统一的标准进行摆正,便于后续进行除杂等操作。
点云摆正就是使全局坐标轴在点云中的位置和姿态明晰,结合钢轨的布置方向与钢轨点云的几何特征和分布特征,可将点云摆正。
(1)将坐标原点移至轨顶平面点云中心点处。
(2)使Z轴正方向与轨顶平面点云的最大主成分方向一致。
(3)使Y轴正方向与轨顶平面点云中心点的法线方向一致。
(4)使点云质心的x坐标为正值,以固定X轴正方向。
上述摆正方法的前提是找出轨头平面点云,在原始点云空间位姿不明晰的情况下,无法提取出轨头平面点云,因此需要对原始点云进行密度聚类,确保轨头点云单独聚成一类。对每一片聚类点云单独摆正,提取聚类点云摆正后的z=0截面,与标准钢轨轨头截面点云进行相似度评价,找出轨头点云。
截面点云的相似度评价可以用Hausdorff距离衡量,Hausdorff距离是描述两组点集之间相似程度的一种量度[16],给定欧式空间中的两点集A={a1,a2,…},B={b1,b2,…},定义公式如下
H(A,B)=max[h(A,B),h(B,A)]
(3)
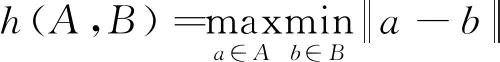
(4)
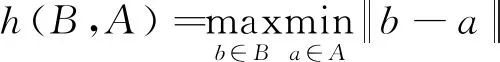
(5)
式中,‖ · ‖为点集A和点集B之间的距离范式;h(A,B)为从点集A到点集B的单向Hausdorff距离,描述了点集A中的点到点集B中点最小距离的最大值,h(B,A)同理。H(A,B)为单向距离h(A,B)和h(B,A)两者中的最大值,称为双向Hausdorff距离,它度量了两个点集间的最大不匹配程度,该值越小,表明两个点集越相似[17]。因此,计算聚类点云截面与标准轨头截面之间的Hausdorff距离,找出其中的最小值,便可提取出轨头平面点云。
将各聚类点云截面与标准轨头截面之间的Hausdorff距离升序排列,依次对原始点云进行摆正,具体摆正流程见图3。摆正效果如图4所示。
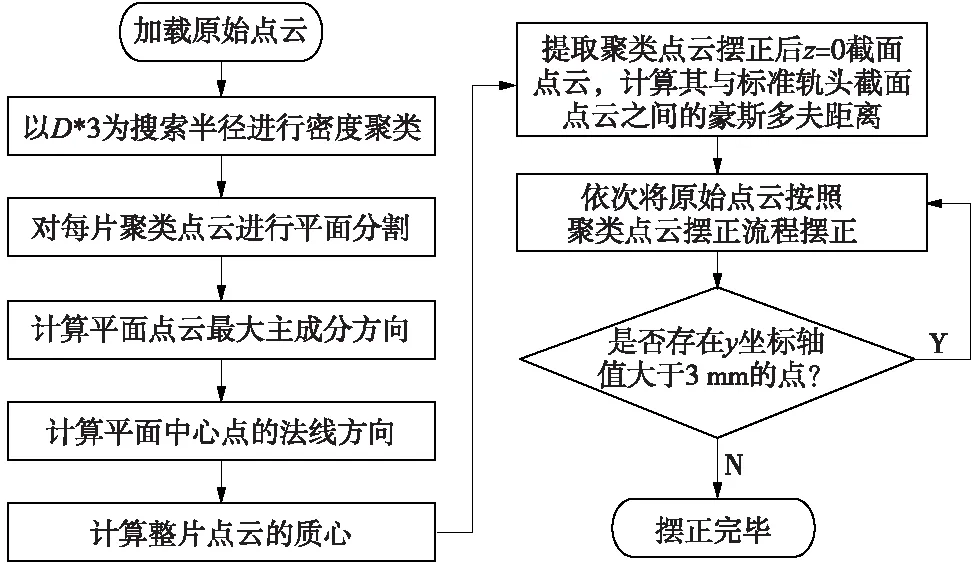
图3 钢轨点云摆正流程
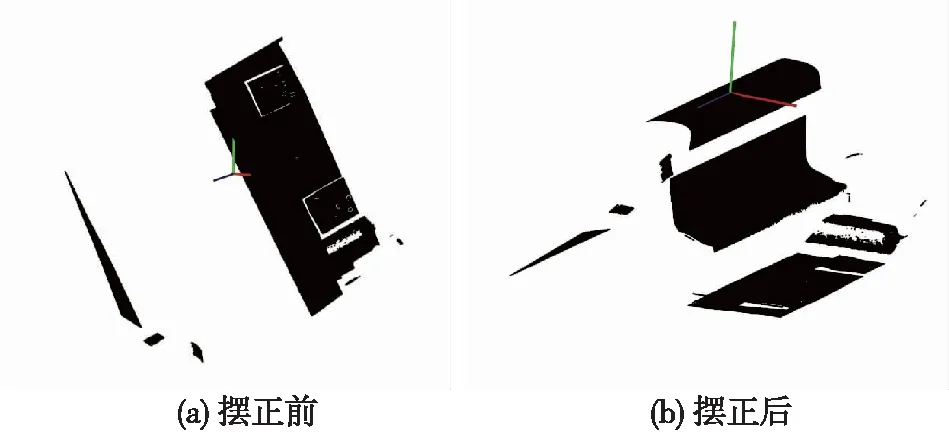
图4 钢轨点云摆正效果
2 点云精简
2.1 密度聚类去除离群点
由铁路现场钢轨点云采集环境和采集设备的放置位置及角度可知,原始钢轨点云中的离群点全部位于轨底附近,其聚类点云的最大y坐标值均不超过轨头聚类点云和轨腰聚类点云的最大y坐标值,因此可以按照空间位置去除离群点。对摆正后的原始点云进行欧式聚类分割,将分割后的点云按最大y坐标值由大到小排序,保留最大y坐标值前两片聚类点云,即可完成离群点的去除。
2.2 直通滤波去除噪声点
直通滤波器可以根据实际需求,在X、Y、Z三个方向维度上设置一个阈值范围,快速裁剪掉阈值范围以内或者以外的点[18]。该滤波器对原始点云的位姿要求较高,如果原始点云的位姿不明确或者不规则,将导致滤波效果不明显,甚至将所需要的点云滤掉。钢轨点云在摆正后,其位姿已经明确,故而可以采用直通滤波器。铁路现场采集的钢轨点云中,除了可以分割出来的离群点,还存在与轨腰聚类点云底部粘连的噪声点,针对此类噪声点,无法通过欧密度聚类分割将其去除。根据图5所示的60 kg/m钢轨的截面尺寸,可以利用直通滤波器,以轨腰侧面为基准,滤掉x坐标值大于66.75 mm的点。

图5 60 kg/m钢轨截面尺寸(单位:mm)
2.3 体素滤波
原始钢轨点云在完成杂点去除后,仍然存在点云数据量庞大的问题,需要对点云进行精简。为了保证点云最终检测结果的真实性,精简后的点云应该与原始点云保持一致的形貌特征及重要细节信息,同时数据规模有所精简。体素滤波是点云处理中一种常见的滤波方法,该方法通过AABB包围盒对点云进行网格化处理,将整个点云划分为一个个的三维体素栅格,然后将每个体素栅格内的所有点都用它们的重心点表示,大大降低了原始点云的数据规模,同时保留了原始的形貌特征[19]。
2.3.1 位姿对滤波结果的影响
针对铁路现场点云的不同位姿,使用相同的三维体素栅格对其滤波。从图6及表1可以看出,在不同的位姿下,精简后点云的数量和分布情况都有较大不同。分析原因得知,三维体素栅格的每一条边都和坐标轴平行,点云的位姿不同,其在不同坐标轴方向上的分布情况不一致,导致每个包围盒中的点数不一样,影响滤波的效果。
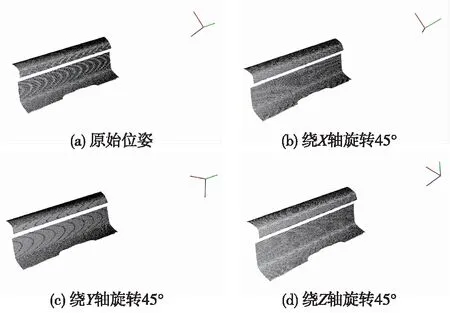
图6 不同位姿下相同三维体素栅格的滤波效果
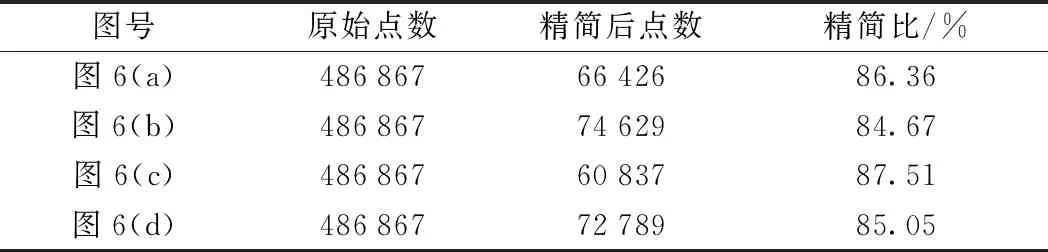
表1 不同位姿下点云滤波精简比
2.3.2 分层滤波
摆正后的点云位姿以及其在各个坐标轴方向上的分布情况已经明确,因此可以很好的规避点云位姿对滤波结果造成的影响。将摆正点云分成三部分:主要分布在X轴和Z轴两个维度的红色水平平面点云,主要分布在Y轴和Z轴两个维度的绿色竖直平面点云以及在X、Y、Z三个维度上均匀分布的黑色曲面点云,如图7(a)所示。分层滤波后的结果如图7(b)所示,点云分布较均匀,曲面点云的细节信息也保留更加完整,点云数量由486 867精简至86 654,精简比为82.2%,耗时低于1 s。
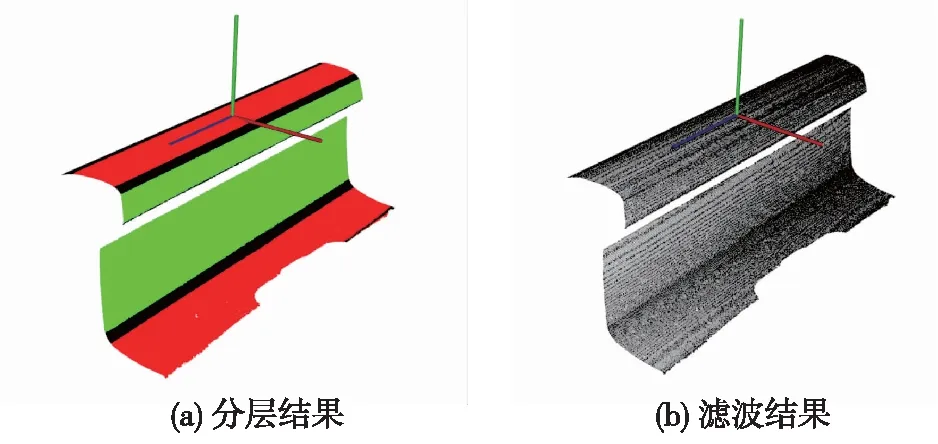
图7 点云分层滤波
3 现场试验与数据处理
铁路现场环境复杂多变,钢轨点云中的杂点形式也多种多样,为了测试上述点云精简方法在铁路现场条件下的有效性与普适性,在成都铁路局工务大型养路机械运用检修段进行了现场试验。
3.1 现场试验
使用自制的轨道测量平台对现场钢轨进行扫描,如图8所示。测量平台包括轨道检测小车、集成了4台相机和1台蓝光投影仪的结构光扫描系统、笔记本电脑以及自行研发的检测软件。

图8 铁路现场试验
将扫描得到的钢轨点云导入检测软件进行数据精简,精简结果如图9所示。

图9 铁路现场条件下的钢轨点云精简情况
3.2 精度分析
点云配准的目的是找出源点云和目标点云之间的旋转平移矩阵,将其统一到相同的坐标系下,方便源点云和目标点云之间的评估。采用Besl等[20]提出的迭代最近点算法(Iterative Closest Point,简称ICP)对点云进行精确配准,但是该算法对两片点云的初始位姿要求较高,否则很容易陷入局部最优,导致配准失败[21]。在点云摆正的基础上,只需将检测点云轨头质心与标准点云轨头质心重合,即可为ICP配准提供一个良好的初始位置,然后提取检测点云的轨腰点云和标准模型点云完成精配。在配置为Intel Core i5-9300H,CPU主频2.40 GHz,内存32 G的计算机上,在Window10系统下编写C++程序进行配准测试。
计算两片轨腰点云之间的点对均方根误差,可以表示配准效果的好坏,但是无法衡量ICP配准的精度。为了分析配准精度,需要对轨腰点云进行平面拟合,分别拟合出轨道竖直平面和轨底平面,然后计算出检测点云和模型点云中对应点云到这两个平面的平均距离。为了消除平面拟合误差,将检测点云与模型点云对应的平均距离相减,以该差值作为点云的配准精度,如表2所示。
滤波后的点云与滤波前相比,在配准效果方面没有明显差距,两者点对均方根误差约为0.4 mm,配准精度约为0.1 mm,但是滤波后的点云配准时间更短,处理效率提高了近4倍。

表2 配准精度分析
钢轨点云配准完毕后,可根据检测需求,提取出测量截面,检测软件通过测量截面与标准钢轨截面的对比,即可计算出该截面的侧磨值、垂磨值以及总磨值。选取其中两个截面,将软件测量结果与接触式JTMH-B钢轨磨耗尺手工测量结果进行对比,如表3所示。
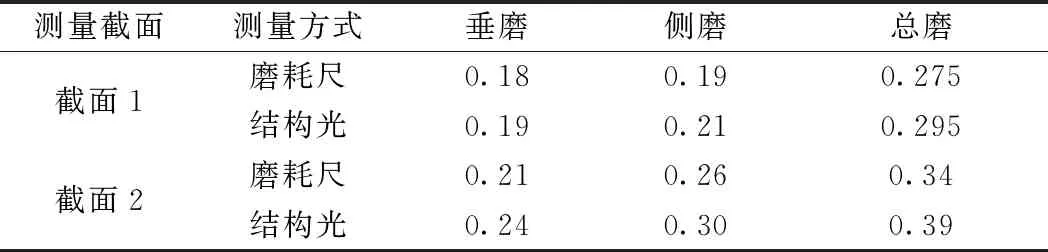
表3 钢轨磨耗测量结果 mm
从表3可以看出,结构光与磨耗尺的测量结果基本相近,均满足《铁路线路修理规则》[22]中对钢轨伤损程度的检测要求。
4 结语
(1)根据钢轨点云的几何特征和分布特征对钢轨点云进行摆正,消除了原始点云的位姿对点云除杂、滤波的影响。在此基础上采用密度聚类和直通滤波实现了对杂点的完全去除,针对不同部位的点云实现了分层滤波,在精简点云的同时,最大程度地保留了点云的重要细节特征。上述处理算法的相关参数均实现了点距自适应,提高了算法的鲁棒性。
(2)现场试验结果表明,本文的点云精简算法,在复杂多变的铁路现场环境下具有普遍适用性;精简后的点云在数据规模降低的同时,也为精确配准提供了良好的初始位置,提高了处理效率。

