月球探测器着陆过程羽流热效应数值模拟研究

张 熇，吴成赓，刘立辉，孙 洁，贺碧蛟，蔡国飙

(1. 北京航空航天大学宇航学院，北京 102206；2. 北京空间飞行器总体设计部，北京 100094；3. 探月与航天工程中心，北京 100086)

0 引 言

月球作为距离地球最近的自然天体，因其独特的空间位置以及丰富的科学信息，具有极高的探测价值，实现月球表面软着陆是探月工程的重要目标之一。月球探测器月面着陆过程需要变推力发动机进行减速，发动机工作产生的高温高压燃气进入真空环境迅速膨胀扩散形成羽流。着陆过程中探测器与月面距离不断减小，发动机羽流与月面相互作用，不仅直接冲击着陆缓冲机构与探测器底板，还会引发复杂的激波-边界层干扰以及涡现象，恶化探测器下方热环境，产生极大的羽流气动热效应，破坏探测器的正常结构，严重时甚至会导致着陆任务失败。

为确保月球探测器月面安全稳定着陆，必须精准评估发动机羽流的热效应，分析不同状态下羽流对不同部位的热影响，以此为探测器着陆过程的关机策略制定提供支撑，为探测器关键部位的热防护设计提供输入。月球探测器发动机羽流场主要分为连续流区与稀薄流区两部分，具体包括连续介质流、过渡领域流和自由分子流三种流态，涉及到连续流与稀薄流耦合，研究难度大。自20世纪50年代以来，计算流体力学的发展为连续流求解提供了较为完善的方法。在稀薄气体动力学研究方面，国外基于直接模拟蒙特卡洛(DSMC)方法开发了一批通用的计算软件，并针对探测器月面着陆过程的羽流效应分析进行了诸多应用，主要包括：美国约翰逊航天中心的DAC(DSMC Analysis Code)软件、美国康奈尔大学的MONACO计算软件、俄罗斯理论与应用机械研究所的SMILE(Statistical Modeling In Low-density Environment)软件等，国内北京航空航天大学、上海交通大学、中国空气动力研究与发展中心、中国航天空气动力技术研究院等单位基于DSMC方法针对羽流的气动作用特性也开展了一系列数值模拟研究。

月面着陆过程是一个复杂的高度非定常瞬态问题，需要量化评估探测器在距离月面不同高度下发动机羽流的热效应，分析月面坡度的存在对羽流热效应的附加影响。在探测器的触月缓冲过程中，因为惯性发动机出口可能与月面逼近至更小距离而恶化底部热环境，同时发动机若出现延时关机或拖尾效应，所产生的羽流热影响也需要加以研判。因而有必要开展探测器高度、月面坡度和发动机状态对羽流热效应的影响研究。本文基于差分求解N-S方程与DSMC耦合的方法，数值模拟不同条件下的发动机羽流场，获取探测器表面受羽流气动作用后的热流密度分布，研究探测器高度、月面坡度和发动机状态对热流密度分布的影响规律，最终评估月球探测器着陆过程的羽流热效应。

1 数值模拟方法

流场的稀薄程度可由宏观Knudsen () 数描述，=/，其中是平均分子自由程，为流场特征长度。当< 0.01时，流场可视为连续流，数越大则流场稀薄程度越高，基于连续介质假说的N-S方程将失效。月球探测器发动机羽流同时包含连续流与稀薄流的跨流域流动，且还需考虑羽流与月面的相互作用状态，因此目前最为高效与实用的数值模拟方法是根据流场稀薄程度不同，对流场进行合理分区以及正确设置分界面，进而基于不同适配的数学物理模型分别求解。本文通过差分求解N-S方程计算探测器与月面特定相对高度、角度状态下的发动机喷管内流场与近月面流场，在N-S方程求解结果的基础上使用DSMC方法对外围羽流场完成进一步计算。

1.1 差分求解N-S方程

采用有限差分、有限体积方法对N-S方程进行求解，控制方程主要包括：

连续方程：

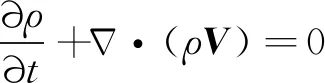
(1)

动量方程：

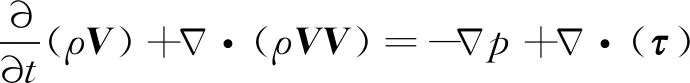
(2)

能量方程：

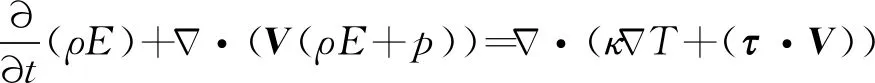
(3)

式中：为密度，为时间，为速度矢量，为压强，为黏性应力张量，为总能量，为热传导系数。

湍流模型选用适应性较好的二方程模型中的SST-湍流模型，以有限体积方法离散微分方程组。时间推进采用LU-SGS隐式方法，每一单元采用局部时间步长。空间推进采用AUSMP迎风格式。

1.2 DSMC方法

DSMC方法直接从物理实际出发，利用少量的模拟分子代替真实流场内数目众多的气体分子模拟计算物理过程，经统计平均获得宏观流动参数，达到求解稀薄气体问题的目的。

基于DSMC方法针对稀薄流区进行求解时，因为流场密度、温度相对较低的特点，可作如下假设：流场中分子的碰撞均为二体碰撞；仅考虑分子转动内能，忽略分子振动内能和分子化学非平衡效应；气体流动为定常流动；分子统一视为变径硬球分子(VHS)。DSMC方法以跟踪统计粒子、实现粒子相对时间的随机演化为特征，具有继承性强、可靠性高、通用性好等诸多优点，是解决稀薄气体流动问题的有效方法，目前已经广泛应用于工程实践。

北京航空航天大学基于DSMC方法自主研发了羽流效应计算软件PWS，软件设计过程中依据模块化原则引入面向对象的编程思想，创新性地提出了流场与边界解耦的高精度网格处理方法、区分粒子碰撞和运动的可变时间步长方法、针对多组分气体的可变粒子权重方法，有效解决了常规DSMC方法在复杂边界描述困难、计算量大等方面的一系列难题，成功实现了PWS软件在羽流效应数值模拟上的通用化应用。

1.3 数值模拟校验

基于美国卡尔斯本大学巴法罗研究中心(CUBRC)在高能激波风洞中试车的实验数据,校验PWS软件的数值模拟精度。CUBRC实验测量了稀薄超声速来流对双圆锥体的气动力热数值，其中来流工质为氮气，来流压强为2.23 Pa。

图1为PWS数值模拟得到的双圆锥体流场马赫数和流线分布图。结果显示，超声速来流在双圆锥体前形成了多道斜激波，激波的交汇处(即双圆锥面的交接处附近)流动较为复杂且形成了明显涡流，气动热影响较为严重。

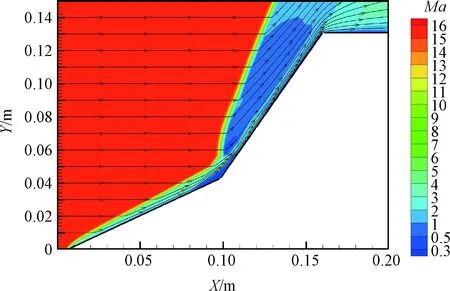
图1 数值模拟校验马赫数及流线分布图

PWS数值模拟得到的双圆锥体表面热流密度数值结果与CUBRC实验结果如图2所示。对比可得，数值模拟与实验结果变化趋势一致、大小基本相符，偏差在-26%～+10%范围内，在流动复杂的涡流区域符合较好。因此，本文认为PWS软件的羽流热效应数值模拟结果具有较高的精度。

图2 双圆锥体表面热流密度数值模拟结果与实验数据

2 探测器羽流热效应数值模拟

2.1 连续流区数值模拟

连续流区包括发动机喷管内流场及近月面流场，数值模拟结果主要用于截取粒子入口截面，以作为稀薄流区的粒子布入条件。本文以某型月球探测器为参考，设定探测器在着陆过程中主要采用变推力发动机的2500 N工作模式进行减速，发动机混合比为1.572，燃烧室总压为0.267 MPa。通过热力计算确定总温为2836.5 K，获得燃烧产物的组分质量分数列于表1。

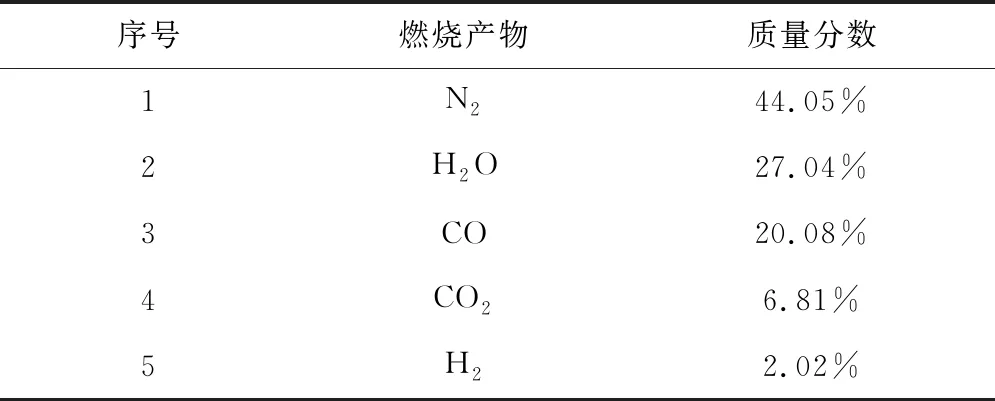
表1 发动机2500 N工作模式主要燃烧产物质量分数

综合以上条件作为连续流区数值模拟的压强入口，发动机内壁面属性设置为无滑移绝热壁面，其余边界设置为压强大小为0的压强出口，通过差分求解N-S方程得到包括发动机喷管内流场与喷流近月面流场的连续流区数值模拟结果，其中探测器相对月面无偏角工况采用二维轴对称计算模型，有偏角工况采用三维计算模型，图3为典型高度连续流区的求解结果示例。

图3 典型高度连续流区求解结果马赫数分布图

在连续流区设置分界面截取入口条件时，为确保流场计算结果有效，同时避免受到下游流场干扰，分界面所在位置流场需满足<0.01以及>1，并且尽量避开发动机喷管下方核心区的复杂波系。

对于发动机喷管出口与月面间距离较小工况，为避免月面反射羽流对入口条件产生影响，分界面选取为喷管出口向轴线方向延伸至月面所得的一个母线倾角为30°的圆台侧面(图3中右侧的深色虚线)。对于发动机喷管出口与月面间距离较大工况，出口位置基本不受月面反射羽流的影响，分界面可直接选取为喷管出口。

2.2 稀薄流区数值模拟

稀薄流区数值模拟采用PWS软件三维计算完成。DSMC计算域以粒子入口截面为起始面，沿粒子主流扩散方向进行扩展设置。经进一步添加探测器几何模型和流场空间体网格，即可完成发动机羽流场的求解，最终获得羽流与月面、探测器相互作用后探测器表面的热流密度分布。

探测器几何模型包括探测器主体、着陆缓冲机构与发动机，在仿真中作为几何包络边界模拟探测器的真实表面。几何模型表面主体采用结构化的直角面网格，物面边界连接区域采用非结构化的三角面网格。面网格主要参与同模拟羽流分子的相互作用计算过程，并记录存储产生的热流密度，以此分析着陆过程中探测器重点位置受羽流气动热效应后的具体影响。

流场空间计算体网格配置以涵盖探测器主要关注部位以及控制计算量为原则，体网格类型选择正交化直角网格，结构划分以粒子分布密度为标准，在数密度大的区域进行合理加密。对于无偏角的对称工况，计算域可结合探测器主体的对称特性，单独划分探测器的1/4区域进行数值模拟。图4为网格划分及入口截面的示意图，该工况下发动机喷管出口与月面间距离较小，在连续流区设置分界面截取得到的粒子入口条件即为图中右侧的深色表面。进行1/4对称设置后的计算域大小为(1.53 m×2.47 m×2.47 m)，流场体网格尺寸与附近探测器面网格尺寸基本保持一致，在DSMC入口截面和月面附近进行了适当加密，最小网格尺度为5 mm。

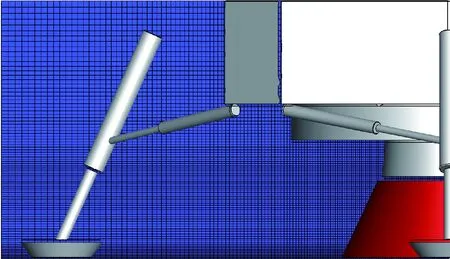
图4 数值模拟网格划分及入口条件示意图

2.3 典型数值模拟结果

根据上述数值模拟结果获取着陆缓冲机构与探测器底板的热流密度数值，进而分析探测器着陆过程羽流气动热效应的影响。

图5为发动机出口中心距离月面0.434 m时，在发动机2500 N工作模式羽流影响下的探测器表面热流密度分布图。结果表明，着陆缓冲机构上受到的羽流气动热影响显著严重于探测器底板，且不同部位热流密度的分布特征区别明显。在此条件下，着陆缓冲机构上从支柱到足垫的热流密度总体呈逐渐减小的变化趋势，探测器底板上从中心到边缘的热流密度总体呈逐渐增大的变化趋势。

图5 探测器表面气动热流密度分布

3 结果与讨论

3.1 着陆高度影响分析

为评估着陆过程中,不同时刻探测器受发动机羽流热效应的影响程度，设置8个工况数值模拟并对比着陆缓冲机构与探测器底板的热流密度数值。本节8个工况发动机出口中心与月面间距离分别为3.08 m,2.68 m,2.28 m,1.88 m,1.48 m,1.08 m,0.757 m与0.434 m；发动机工作模式为2500 N；月面无坡度；月面温度为300 K。

着陆缓冲机构主要分为支柱与足垫两部分，如图6所示。在支柱上重点关注关键点P,P,P,P,P，在足垫上设置关键点P,P,P。

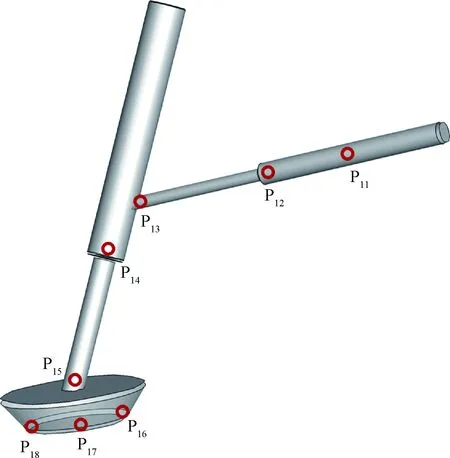
图6 着陆缓冲机构关键点分布示意图

图7为发动机以2500 N模式在不同高度工作时，着陆缓冲机构上各关键点的热流密度随发动机出口与月面间距离的变化关系。当发动机出口中心距离月面在2.28 m以上时，着陆缓冲机构上的热流密度均在10 kW/m以下。当距离减小到1.48 m时，着陆缓冲机构上的热流密度开始突破100 kW/m。

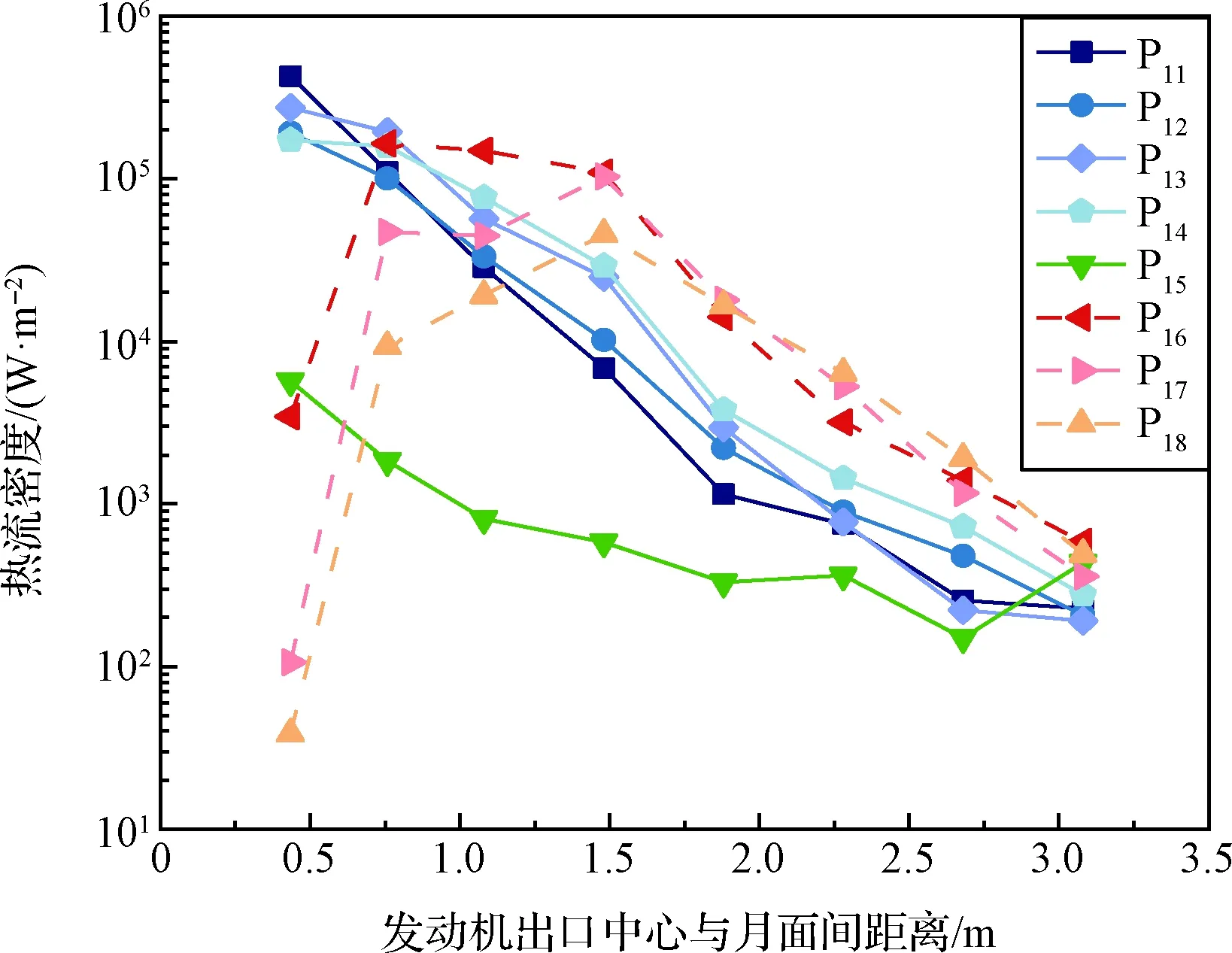
图7 着陆缓冲机构关键点气动热流密度随距离变化关系

在探测器下降过程中,随着距离减小，支柱表面(P～P)的热流密度近似呈指数增加，当发动机出口中心距离月面0.434 m时，支柱上热流密度达到最大值，约为429 kW/m。在探测器下降过程中随着距离减小至1.48 m，足垫表面(P～P)的热流密度增加规律与支柱相似，但随着距离进一步减小，呈现出减小的趋势。当发动机出口中心距离月面在0.757 m～1.48 m时，足垫表面各点热流密度相继达到最大水平，其中最大值约为165 kW/m。

在探测器底板上设置关键点P,P,P,P,P,P,P，分布图如图8所示。

图8 探测器底板关键点分布示意图

图9为发动机以2500 N模式在不同高度工作时，探测器底板上各关键点的热流密度随发动机出口与月面间距离的变化关系。当发动机出口中心距离月面在2.28 m以上时，探测器底板上的热流密度均在1 kW/m以下。当距离减小到1.48 m时，底板上的热流密度开始突破10 kW/m。

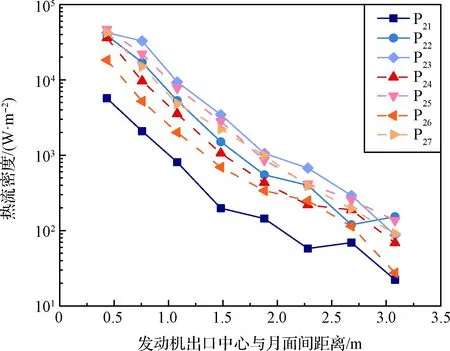
图9 探测器底板关键点气动热流密度随距离变化关系

在探测器下降过程中,随着距离减小，探测器底板上各关键点的热流密度变化趋势基本一致，总体上近似呈指数增加，当发动机出口中心距离月面0.434 m时，热流密度达到最大值，约为47 kW/m。在相同高度下，探测器底板边缘位置关键点的热流密度相比靠近中央位置的关键点更大。针对所取关键点按P～P,P～P,P～P三组分别进行对比，结果显示越接近探测器底板边缘的关键点热流密度更高。

为探究随着陆高度减小,探测器不同位置受发动机羽流热效应影响程度的变化规律，需结合流场图进一步分析，图10为探测器在三个典型高度下的羽流场压强分布图。

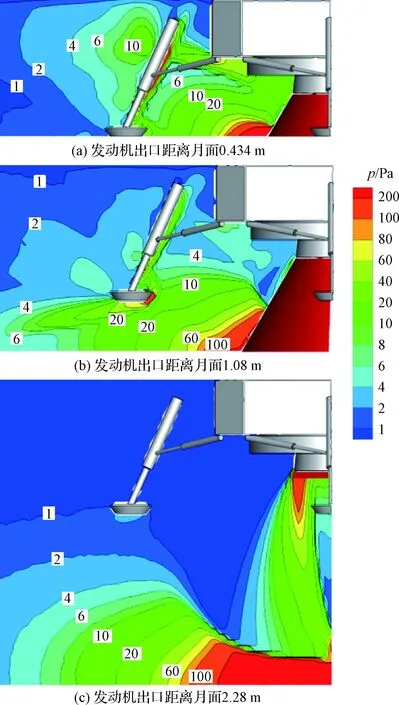
图10 不同着陆高度下探测器羽流场压强分布图

不同着陆高度下的流场结果显示，在探测器下降过程中，随着发动机出口与月面间距离不断减小，羽流与月面作用反射产生的返流可逐渐扩散至着陆缓冲机构的支柱上，且作用强度不断增强，使得支柱上各关键点热流密度总体呈单调上升趋势。随着探测器高度不断减小，羽流相对足垫表面的入射角度和作用强度不断变化，当发动机出口距离月面在1.08 m左右时，羽流在足垫上的滞止作用最剧烈，而随着陆高度进一步减小，足垫周围羽流与月面更为接近，受到月面的冷却作用更强，羽流的能量特性进一步降低。综合以上原因，随着陆高度减小，足垫上关键点的热流密度变化呈现先增大后减小的趋势。

不同着陆高度下的流场结果表明，在探测器下降过程中，随着发动机出口与月面间距离不断减小，探测器底板下方羽流场压强逐渐增大，羽流作用强度不断增强，因此底板上各关键点的热流密度随距离减小总体上也呈单调增大趋势。由于探测器下方的中央位置靠近发动机为高压区，边缘位置因外部真空环境影响为低压区，结合流场图可以判断，羽流与月面作用后的向上反射过程具有强烈的向外扩散特征，底板边缘下方相对中央位置流场压强更大，因此受到的气动热效应影响也更为严重，印证了高度相同时底板上靠外侧关键点热流密度相比内侧更大的规律。

3.2 月面坡度影响分析

实际着陆过程中,落月位置可能存在坡度，为评估月面坡度对探测器着陆过程发动机羽流的热效应影响，在发动机出口轴线与月面有无偏角的两种状态下共设置8个工况，分析着陆缓冲机构与探测器底板上羽流气动热流密度的最大值大小。偏角大小由着陆过程中可能出现的极限角度确定为12°，考虑到发动机出口距离月面2.28 m以上时探测器受羽流热效应影响较小，因此只设置距离不大于2.28 m的工况，图11为有无偏角状态下着陆缓冲机构与探测器底板热流密度最大值随距离的变化关系。

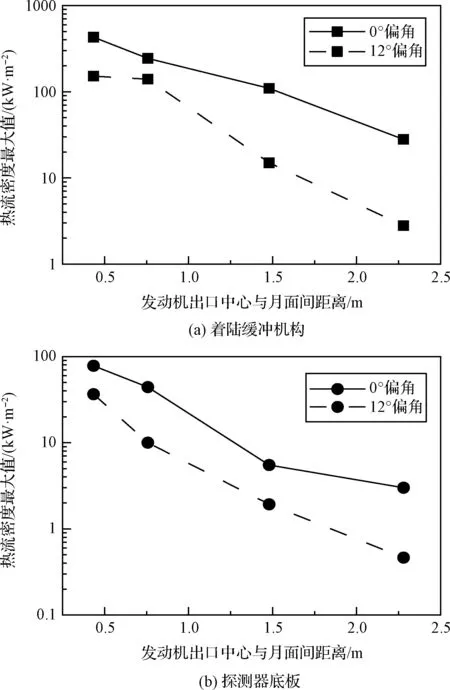
图11 探测器相对月面不同姿态着陆缓冲机构与底板热流密度最大值随距离变化关系

数值模拟结果显示，当发动机出口中心与月面间距离相同时，着陆缓冲机构与探测器底板上的热流密度最大值在有偏角状态下均小于无偏角状态。针对羽流的流动状态进行分析，当落月位置存在坡度时，探测器底板与月面不平行，探测器下方一侧区域空间更大，具有更强的导流作用，有利于羽流的扩散膨胀。存在坡度时，发动机羽流与月面的作用过程将由近似垂直正入射变为斜入射，有助于减弱羽流的压缩减速与滞止作用，减小羽流导致的气动热效应，最终改善探测器周围的流场热环境。

本文研究结果表明，月球探测器着陆过程中月面坡度的存在对羽流气动热效应无加剧作用，落月位置无坡度状态相对有坡度状态，发动机羽流对探测器的气动热更恶劣，因此可采用无坡度状态的气动热计算结果指导探测器的热防护设计。

3.3 缓冲过程惯性及延时拖尾效应影响分析

月球探测器着陆过程因落月惯性、关机信号延时、发动机拖尾等因素影响可能存在特殊工况，在羽流热效应数值模拟研究中，需要考虑的主要包括缓冲过程发动机出口与月面达到极限距离以及发动机关机的延时拖尾效应两类情况。为探究上述因素的影响程度，共设置12个工况。其中，选取发动机2500 N模式距离月面0.234 m条件下的工作状态研究落月惯性的影响，选取发动机1000 N, 500 N两种模式分别距离月面1.08 m, 0.757 m, 0.434 m与0.234 m条件下的工作状态研究发动机延时拖尾效应的影响。

发动机在2500 N, 1000 N与500 N工作模式下着陆缓冲机构与探测器底板热流密度的最大值随距离的变化曲线如图12所示。

图12 发动机不同工作模式探测器关键部位气动热流密度最大值随距离变化关系

数值模拟结果表明，随着发动机出口距离减小，着陆缓冲机构与探测器底板上热流密度最大值增加。当距离由0.434 m减小到0.234 m时，着陆缓冲机构上热流密度最大值急剧升高至888 kW/m，约为0.434 m状态下的两倍。探测器底板上热流密度最大值增幅较小，由0.434 m状态下的78 kW/m略微增长至81 kW/m。由此可见，探测器在触月缓冲过程中，若因惯性导致发动机出口与月面间距离减小至极限状态(0.234 m)后，着陆缓冲机构附近热环境将进一步恶化，而探测器底板受到的气动热效应变化较小。

数值模拟结果显示，当发动机处于1000 N工作状态时，于0.434 m高度在探测器上产生的最大热流密度为154 kW/m，于0.234 m高度产生的最大值为399 kW/m。相同高度下，发动机以1000 N工作模式在着陆缓冲机构与探测器底板上产生的热流密度最大值基本处于2500 N模式下的40～60%范围内。当发动机处于500 N工作状态时，于0.434 m高度在探测器上产生的最大热流密度为71 kW/m，于0.234 m高度产生的最大值为167 kW/m。相同高度下，发动机以500 N工作模式在着陆缓冲机构与探测器底板上产生的热流密度最大值约为2500 N模式下的20%。

综上所述，落月惯性导致探测器发动机出口与月面间距离逼近至0.234 m后，羽流与月面相互作用将进一步加剧探测器受到的气动热效应；发动机关机过程的延时及拖尾效应依然对探测器具有一定程度的热影响，但产生的热流密度最大值明显小于以2500 N模式工作时的对应数值，且大致比例与推力大小近似相关。

4 结 论

本文针对月球探测器着陆过程羽流热效应进行了数值模拟研究，通过差分求解N-S方程与DSMC耦合的方法完成了发动机喷管内流场、近月面流场与外围羽流场的数值模拟，获得了探测器表面不同条件下受羽流气动作用后的热流密度分布，研究结果表明：

1) 探测器受到的羽流气动热效应总体随着陆高度的减小急剧增强，在着陆高度为3.08 m至0.434 m范围内，着陆缓冲机构和探测器底板关键点的热流密度最大值分别为429 kW/m和47 kW/m；当着陆高度大于2.28 m时，着陆缓冲机构和探测器底板受羽流气动热效应的影响较小，热流密度均小于10 kW/m。

2) 当月面存在坡度时，因导流作用及羽流入射角度改变，探测器受羽流气动热效应影响相对同高度无坡度状态更小。

3) 因落月惯性导致探测器发动机出口与月面间距离逼近至0.234 m后，着陆缓冲机构与探测器底板热流密度最大值分别升至888 kW/m与81 kW/m；当发动机关机过程出现延时及拖尾效应时，探测器将受到一定程度热影响，但热流密度最大值明显小于同条件2500 N模式工作状态。