含模型不确定性和状态约束的航天器姿态鲁棒控制

林晓冬，张 锐

(1.中国科学院微小卫星创新研究院，上海 201203；2.中国科学院大学，北京 100049)

0 引 言

随着空间信息传输、科学探测和空间遥感的需求迅猛发展，航天器的构型日益复杂、功能日益全面、性能日益提高。在航天器指标提升和任务复杂度的促进下，高效抑制各种未知扰动并同时满足预设的约束条件成为航天器完成预期任务的前提保障，同时也是现阶段航天器姿态控制的研究热点。

航天器姿态控制方法已经被广泛研究，如滑模控制，自适应控制，最优控制，障碍函数控制和预设性能控制。文献[13]在理想情况下基于动态切换函数的方法设计了动态滑模控制器。文献[14]利用分段函数饱和补偿辅助系统和动态面设计了鲁棒姿态跟踪器。文献[15]结合模糊控制和自适应控制设计了鲁棒控制器，有效地抑制了外部扰动。文献[16]基于自适应神经网络控制设计了航天器姿态跟踪控器。文献[17]基于反步法进行控制器设计，利用势函数法构造约束条件有效地解决了规避多个禁止指向区域的姿态机动问题。文献[18]针对充液航天器提出了一种固定时间终端滑模控制策略，控制器设计过程中考虑了外部未知干扰、参数不确定性和输入饱和等因素的影响。文献[19]基于固定时间概念完成了终端滑模自适应控制器的设计，引入正弦函数切换项和双幂次项，有效地抑制外界扰动并提高了系统控制精度。文献[20]针对具有模型不确定性的刚性航天器输入受限时的姿态跟踪控制问题设计了鲁棒自适应状态反馈受限控制器。文献[21]针对刚性航天器姿态跟踪问题，提出了一种全状态约束输出反馈控制器，可以保证系统全状态约束性能和姿态跟踪精度。文献[22]设计了新型的快速鲁棒输入成型器和自适应连续终端滑模控制器，有效地抑制了各种外界扰动提高了控制精度和收敛速度。文献[23]针对航天器姿态控制系统存在系统不确定性的情况，基于两相幂次趋近律设计了鲁棒姿态控制器。文献[24]针对航天器全状态约束问题，基于障碍李雅普诺夫函数设计了状态反馈控制器。文献[25]针对航天器姿态约束问题，采用预设性能函数和误差变换方法，完成包含预设性能边界的控制器设计。但上述文献并未同时处理航天器存在模型不确定性、未知外部扰动、时延和状态约束等情况。本文将结合工程实际经验，设计鲁棒控制器有效地解决系统存在的各种扰动问题。

本文创新之处为：(1)利用反步法和障碍李雅普诺夫方法设计了鲁棒控制器，解决了姿态角和角速度的约束问题；(2)基于自适应神经网络方法，解决了系统模型不确定性和未知扰动对姿态控制系统的影响；(3)结合工程实际，采用前馈补偿方法解决了航天器控制系统时延对系统性能的影响；最后根据李雅普诺夫稳定性理论证明了系统状态是最终一致有界的。

1 航天器姿态模型及问题描述

航天器全方位姿态运动可以通过四元数无奇异的表述，且实际工程中高精度定姿敏感器为恒星敏感器，其输出为姿态四元数。综合考虑以上两方面因素，本文采用四元数描述航天器姿态运动并建立误差运动学和动力学模型。

1.1 航天器四元数姿态模型

四元数描述的刚体航天器运动学和动力学模型为：

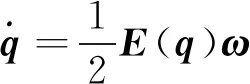
(1)

(2)

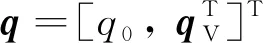
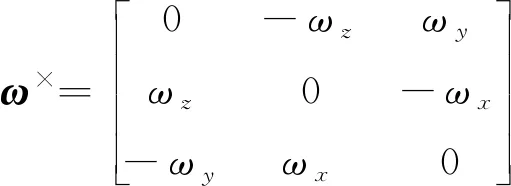
(3)

式(1)中：

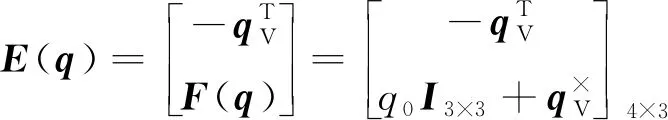
(4)

本体坐标系相对于惯性坐标系的旋转矩阵()形式如下：

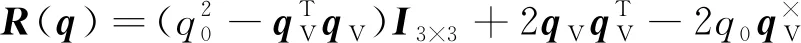
(5)

1.2 航天器误差四元数姿态模型

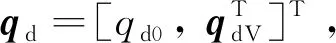
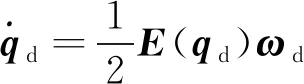
(6)

航天器本体坐标系相对于期望坐标系的误差四元数和误差角速度定义为：

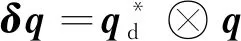
(7)

=-()

(8)

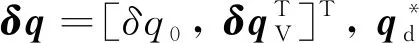
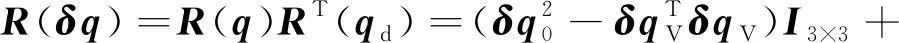
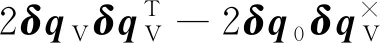
(9)

则姿态误差运动学和动力学方程为：

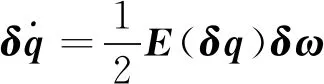
(10)

()++

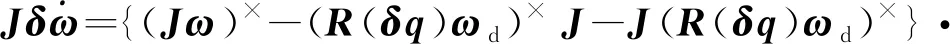
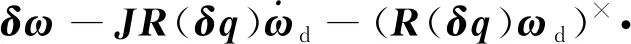
(11)

航天器转动惯量矩阵为=+，其中为标称惯量矩阵，为未知惯量矩阵。

1.3 本文目的

航天器姿态误差运动学和动力学方程如式(10)和式(11)所示，本文在充分考虑航天器姿态控制系统存在时延、模型不确定性和未知干扰的情况下，设计控制器使得航天器姿态控制闭环系统满足以下条件：

1)对各种扰动具有鲁棒性且能够进行有效抑制；

2)跟踪误差和可以满足预设的约束条件，并最终收敛到原点的一个小邻域内。

2 鲁棒控制器设计

2.1 引理及假设

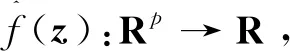
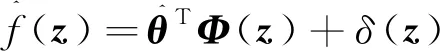
(12)

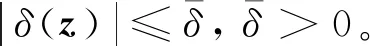
()=()+, ∀∈Ω∈

(13)

式中：为径向基函数神经网络最优权重，其形式如下：

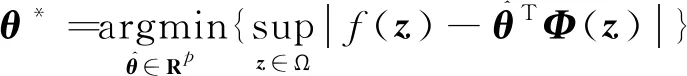
(14)

式中：Ω为状态向量的一个可接受域。

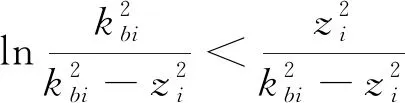
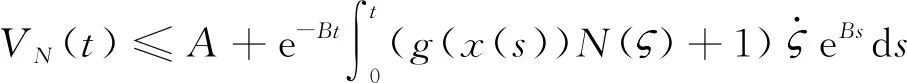
(15)

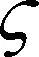
航天器姿态测量系统和控制系统存在有界时延。

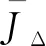
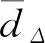
期望角速度和角加速度有界。

实际工程中期望姿态和角速度一般都会预先进行规划处理，这样可以保证角速度和角加速度的有界性，同时也可以保证航天器的安全性。

上述假设在理论和实际工程中都是合理可行的。

2.2 反步法控制器设计

选取变量为：

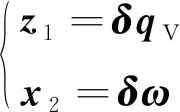
(16)

选取虚拟控制器，形式如式(17)所示，则可以保证误差四元数满足预设的约束条件。

设计虚拟控制器为：

=-

(17)

式中：=diag(,,),1>0,=1,2,3。

由式(10)和式(16)推导整理得：

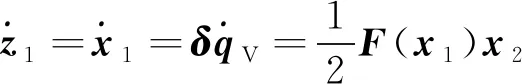
(18)

选取障碍李雅普诺夫函数，形式如下：

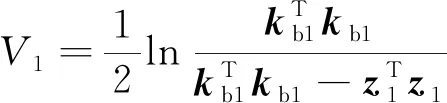
(19)

式中：=[,,],b1>0。

对沿闭环轨迹求导可得：

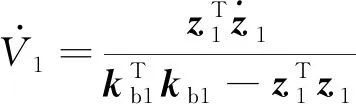
(20)

将式(18)代入式(20)得：

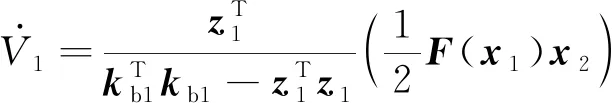
(21)

将虚拟控制器代入上式则有：

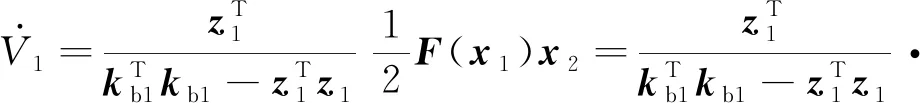
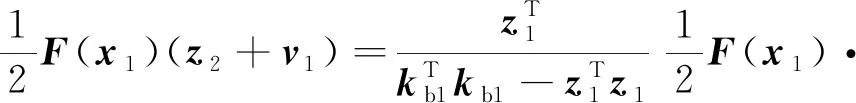
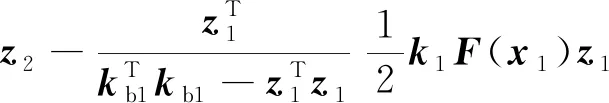
(22)

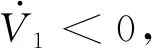
证毕。

基于反步法设计思想，设计变量如下：

=-=-

(23)

针对航天器姿态误差模型(10)～(11)，基于假设1～4，利用自适应控制器(24)和自适应神经网络权重更新律(27)，可以实现如下目标：

1)所有闭环系统信号有界；

2)跟踪角度和角速度误差满足预设的状态约束。

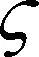
(24)

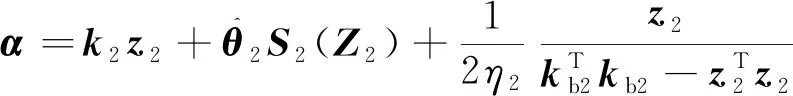
(25)

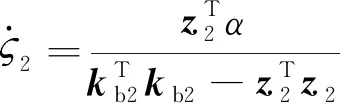
(26)

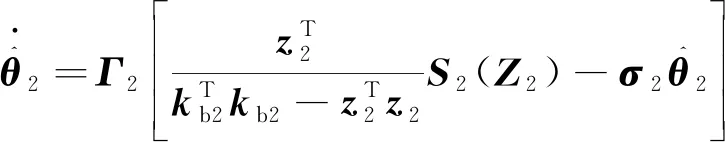
(27)

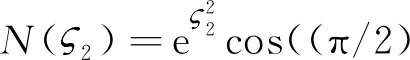
(28)

对求导得：

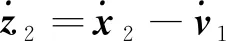
(29)

式(29)中：

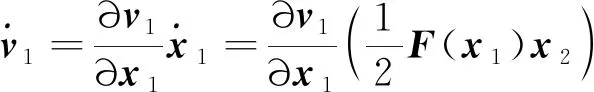
(30)

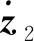
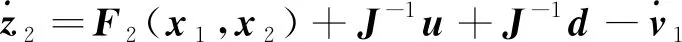
(31)

其中：

(,)={()-(())-

(())()

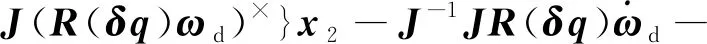
(32)

选取障碍李雅普诺夫函数：

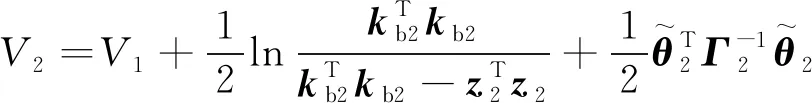
(33)

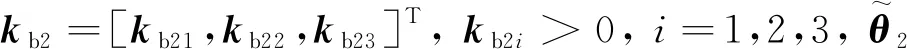
则沿闭环轨迹求导可得：

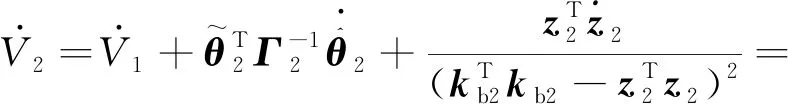
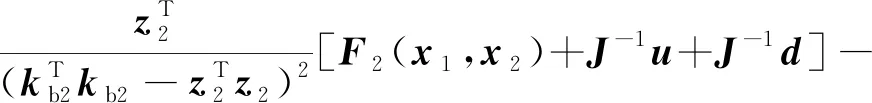
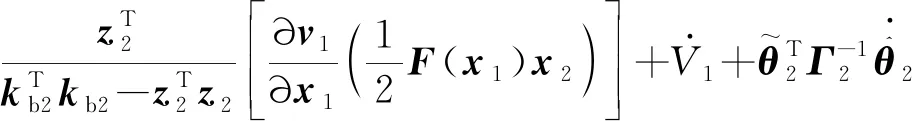
(34)

利用杨氏不等式：

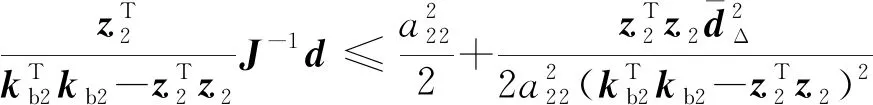
(35)

代入式(34)，整理得：

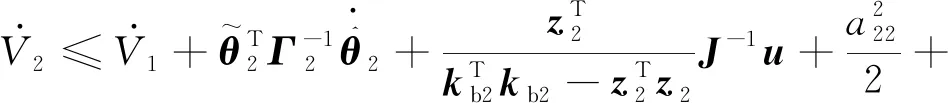
(36)

式中：

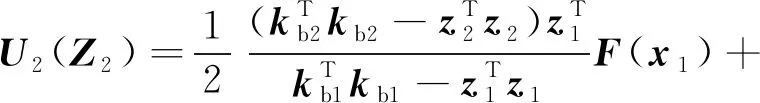
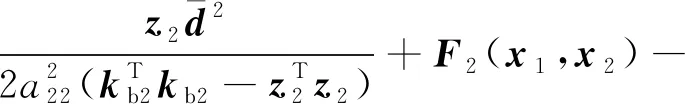
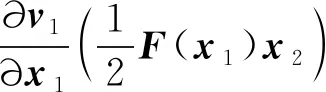
(37)

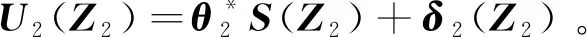
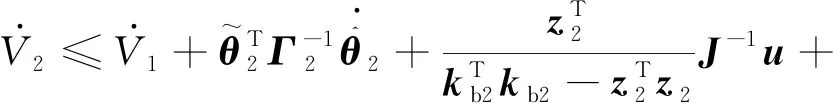
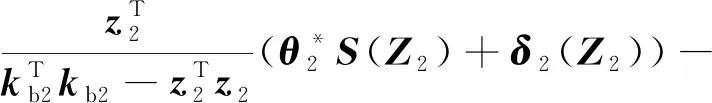
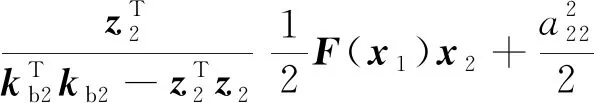
(38)

将式(24)和式(27)代入上式，可得：

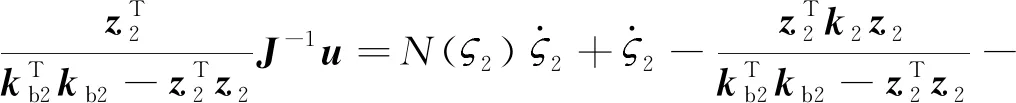
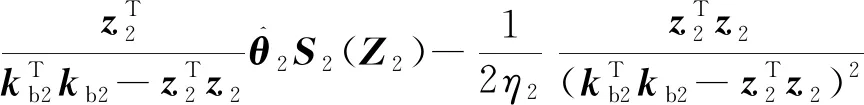
(39)

将式(39)代入式(38)中，整理得：

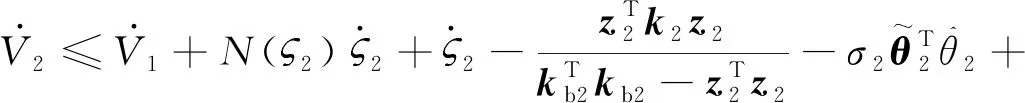
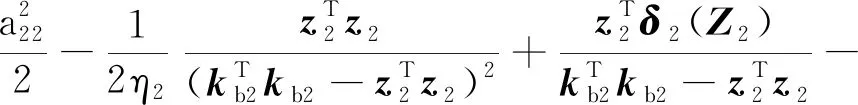
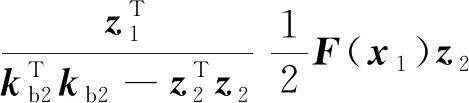
(40)

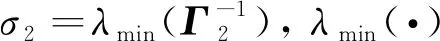
利用如下杨氏不等式：

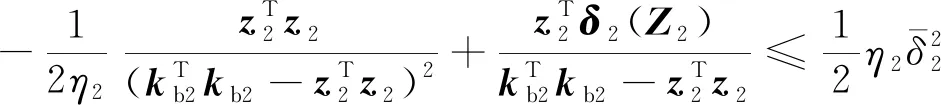
(41)

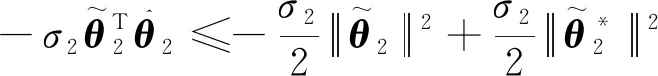
(42)

将式(41)、(42)和(35)代入式(40)可得：

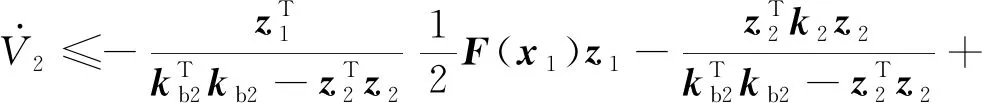
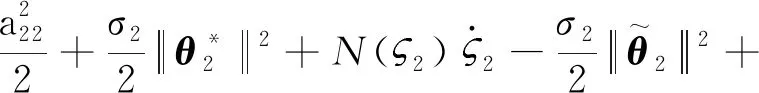
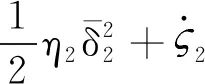
(43)

最终选取李雅普诺夫函数为：

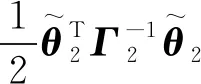
(44)

对求导可得：

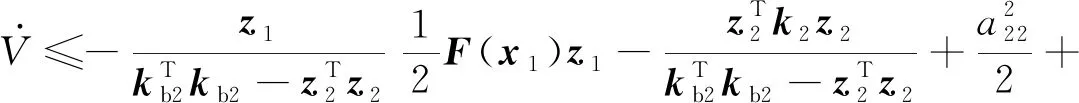
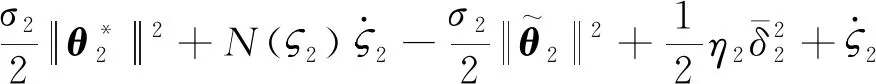
(45)

根据引理2可得：

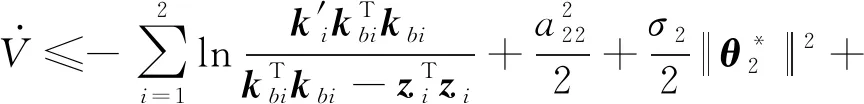
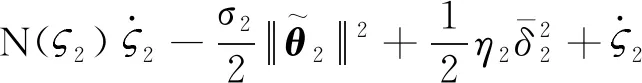
(46)

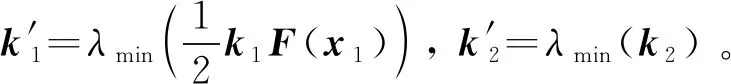
进而式(40)变为：

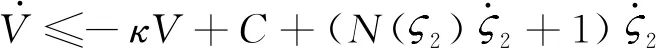
(47)

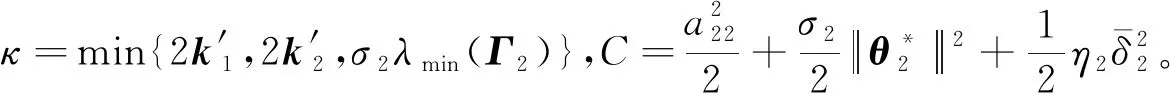
式(47)两边同时乘以exp()，并积分得：

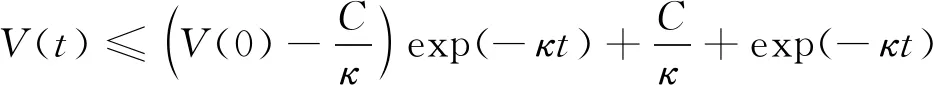
(48)

根据定义可得：

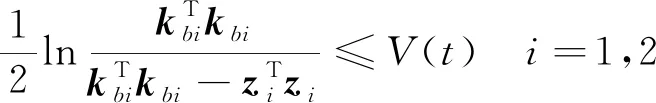
(49)

则可以推导出：

≤·

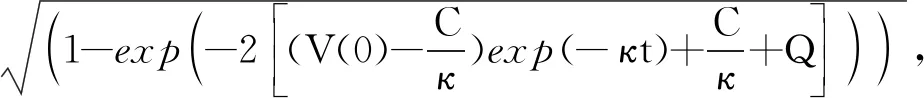
=1,2

(50)

根据式(50)可知，通过本文所设计的鲁棒控制器可以保证闭环系统信号约束条件不被违反，且跟踪误差最终收敛到原点的一个小邻域内。

证毕。

2.3 已知时延前馈修正

本节对航天器控制系统中存在的时延进行前馈补偿修正，一方面消除时延对控制器鲁棒性的影响，另一方面可以提高系统的控制精度。

从工程实际出发，对机理清晰的标称延时，可以采用前馈补偿的方式对其进行预处理。对测量四元数、测量角速度、误差四元数和误差角速度进行处理，处理具体形式如式(51)所示，并将处理后的数据用于控制器时对位置时延的修正。

(51)

式中：为星敏测量得到的惯性系四元数，为陀螺测量得到的本体系四元数，和分别表示星敏感器接收到指令信号后完成曝光获得姿态信息和陀螺单机获得角速度信息到星上定姿程序输出姿态信息的时间间隔；表示星上完成姿态确定到误差计算的时间间隔；表示误差计算完成后星上根据各执行机构状态计算实际控制指令输出的时间间隔。

3 仿真校验

卫星在轨运行时，二维帆板驱动机构摆动角为36°，滚转角以轨道角速度约0.06(°)/s连续转动，保证能源供给。随着帆板的转动，卫星转动惯量及惯量积变化明显。在轨环境干扰力矩主要是由于质量特性变化而引起的重力梯度干扰力矩。

仿真条件：

1) 仿真环境

本仿真采用成熟的半物理仿真平台，框架如图1所示，该平台已在多型号上得以应用和验证。主要组成如下：

图1 半物理仿真平台框架

① 动力学实时仿真系统：用于模拟卫星轨道模型、姿态动力学模型、卫星在轨运行环境模型；

② 星务计算机：定制化，用以运行星载软件，控制频率4 Hz；

③ 姿态敏感器：星敏感器+光纤陀螺；

④ 执行机构：45 N·m·s/0.075 N·m反作用轮+200 Am磁力矩器；

⑤ 敏感器激励：星图模拟器+高精度三轴转台。

2) 初始条件

航天器三轴稳态对地定向模式。

3) 期望跟踪目标四元数和角速度

航天器初始状态为稳态对地定向模式，8000 s时航天器绕Y轴姿态跟踪控制，角速度最大为0.5(°)/s。

4) 未知扰动

=0001[sin(01),cos(02),sin(02)]N·m，

模型参数不确定性：=10%。

5) 控制参数选取

仿真结果：

图2为误差角速度仿真曲线，从图中可以看出，当航天器加速和减速过程中，跟踪误差明显比稳速过程中偏差大，这是由于执行机构输出需要一定的响应时间。图3为执行机构输出力矩曲线。从图4中可以看出，跟踪姿态角速度误差始终在预设的约束范围内，验证了控制器设计的有效性。

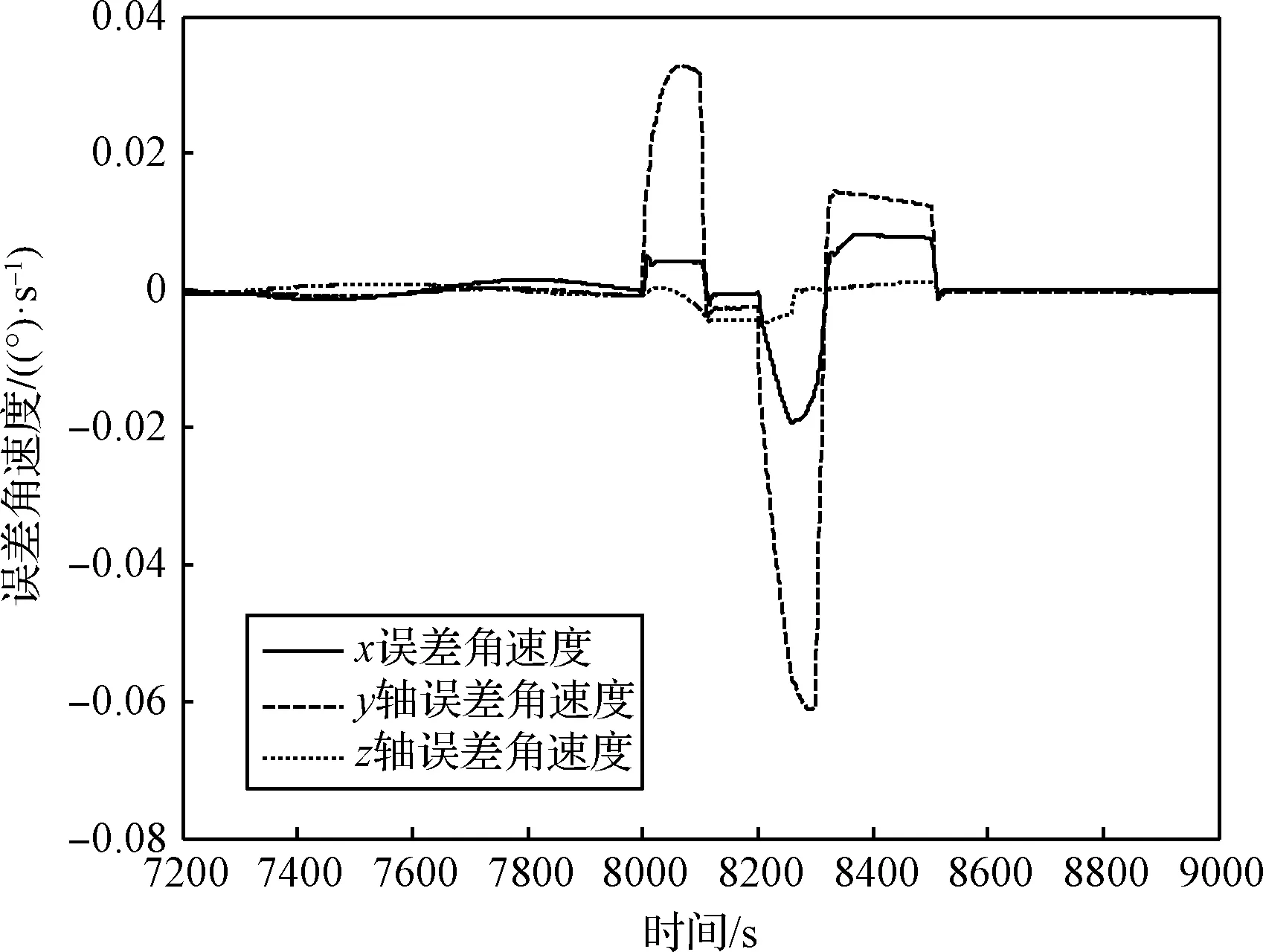
图2 误差角速度曲线

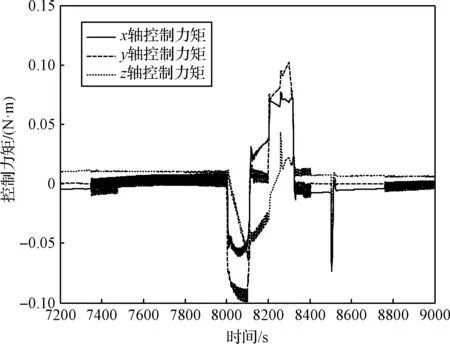
图3 执行机构输出力矩曲线

图4 δω模值与预设约束条件曲线

4 结 论

本文考虑航天器存在各种扰动和状态约束条件下的姿态控制问题。首先结合神经网络和障碍李雅普诺夫函数方法对模型参数不确定性、未知扰动和状态约束进行处理，然后利用反步法设计一种鲁棒自适应姿态控制器，最后结合工程实际经验对已知时延进行前馈补偿。通过理论证明和整星半物理环境下的实际测试表明了本文所提出的控制器设计方法的有效性。