滑道入水流致噪声数值模拟及抑制措施研究
黄黎慧 赵永振 宁小深 李福庚 王子斌 杨 衡*
(武汉交通职业学院船舶与航运学院1) 武汉 430065) (中国舰船研究设计中心2) 武汉 430064)
(哈尔滨工程大学船舶工程学院3) 哈尔滨 150001)
0 引 言
科考平台[1]既可以用于海洋资源勘探,又能进行海洋项目开发,是近年来海洋科学研究的重要助手.但考虑到海洋环境的复杂性,科考平台往往需要借助水下机器人[2]等物体完成信息采集等特殊任务.而物体入水抨击必然会产生流致噪声,影响信息收集的精确性.
针对水下流致噪声的预报和控制,何祚镛[3]介绍了船舶行业水下噪声研究进展概况,包括水下噪声形成机理和预报方法,并提出将有源控制和复合有源结构的理论用于大型结构噪声控制研究.李清等[4]基于URANS方法建立了舰船结构有限元-流体声学间接边界元(FEM-IBEM)声振耦合计算模型,分析了各类噪声源辐射噪声的指向特性和频谱特性,证明了耦合声场计算方法效率和精度更高.李生等[5]采用大涡模拟(LES)方法计算了表面开孔的非定常流场,分析了流场的非定常流频谱特性,分析了增装导流体和圆形挡板对噪声的控制效果.耿冬寒等[6]利用LES计算空腔非定常流动的流场结果,基于FEM利用Lighthill声类比方程进行声场求解,结果表明基频值的预报结果与文献基本一致.刘波等[7]结合FW-H方程,利用VOF方法与SST k-omega湍流模型,对不同球鼻首船型的噪声进行了预报,对船体流噪声的空间指向性、近远场分布特性进行分析.结果表明:CFD技术可以用于模拟分析船舶的绕流场和流致发声问题,能够为低噪声船体线型设计提供参考.王超等[8]为提高水下声学滑翔机水下目标检测能力,定量分析了四种工况下的噪声特性,并从优化转向调节机构与控制策略、阻断噪声传播途径、电磁兼容性和声学系统工作模式优化5个方面进行减振降噪,结果表明,对中高频段噪声降噪效果良好.
物体入水产生的流致噪声具有非线性和瞬时性的特点,如何构建质量良好的声学网格,准确捕捉物体从科考平台入水时的瞬时噪声特性是研究的难点所在.文中基于DES建立了物体由滑道滑动入水的数值模型,结合FW-H模块进行声场求解,分析了物体由滑道入水时的噪声特性,并给出了滑道截面面积优化和增加空腔的抑噪措施.
1 数值原理
1.1 流体湍流模型
流体求解基于分离涡模拟(DES),采用精度较高的SST k-omega二方程湍流模型,其基本方程为
Pk-β′ρkω
(1)
(2)
式中:ρ为流体密度;k为湍流动能;ω为湍流比耗散率;U为流速;F1为混合函数;μ为黏性系数;μt为涡黏性系数;Pk为湍流生成项.
1.2 声学控制方程
Lighthill考虑的模型为:在无限大的均匀、静态声介质中包含一个有限的湍流运动区域V,因此与流动有关的声源都集中在该区域内.在区域V外,远离湍流区域的流体中密度的波动和声波相似,因此整理连续方程和动量方程,简化得到远离湍流区域流体中的匀质声学波动方程:
(3)
式中:c0为等熵条件下的声速值;ρ′=ρ-ρ0,ρ与ρ′分别是扰动与未扰动时的流体密度.
Curle在Lighthill声学类比理论的基础上考虑了一个自由空间V内存在有表面积的固壁面的情况,类似Lighthill的做法,现考虑一外体积为V(τ),包围体积的表面积为S(τ)且运动速度为V的运动物体的发声问题.为
(4)
式(4)多了压力项的影响,利用积分及格林函数的性质,可以消去中括号中的几项.于是得到
(5)
对上式做紧致声源等一系列假定,可以去掉时间项 的影响,于是上式可以整理为一个更为普遍的解
(6)
式中:x和y分别为接收点和声源点的坐标向量;|r|=|x-y|为两点之间的距离向量;|r|/c0为迟滞时间;t为声音从源点辐射到接收点的时间;nj为固体边界表面向外的方向余弦.
2 计算域设置
2.1 几何与边界
滑道几何模型见图1,物体模型置于滑道正中央,模型前端与滑道前端对齐,固定滑道角度为45°.定义特征长度L=100 mm,滑道内径宽度为4.4L、高度为5.6L,滑块为长方体,截面尺寸为3L×3L.

图1 滑道模型
模型的运动为整体的沿着滑道向下滑动,针对模型的运动设置计算域,计算域选择长方体,计算域长50L、宽40L、高35L.计算域划分结果见图2,计算域包括滑道在内的流体域、包括入水模型在内的运动域以及远场域.流体入口和出口分别设置为速度入口和压力出口;周向四个流场界面均为对称平面.

图2 计算域划分
2.2 网格划分
水动噪声计算网格设置与声波波长尺度相关,通常设置一个声波波长包含6个网格长度时可以满足对声波的计算.声波频率越高波长越小,所需的网格尺度越小.本文网格模型选择切割体网格生成器、棱柱层网格生成器和表面重构,整个流体域分成两个部分,一部分是静止的流体域,一部分是运动区域,整体网格采用重叠网格方法,对运动的处理选择滑移网格,网格基础尺度设置为0.012 5 m,壁面Y+取值在10~30之间.网格分布见表1,静止域网格数为475万,运动域网格数为44万.网格划分见图3~4.

表1 网格分布

图3 计算域网格
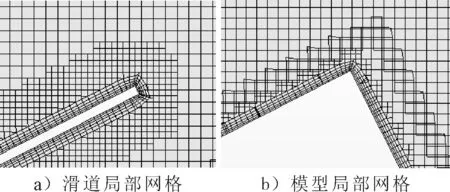
图4 滑道及入水模型局部网格
时间步长通过最大声波求解频率确定:
(7)
当最大求解频率为5 000 Hz时,可求得时间步长为1×10-4s.因此本文噪声求解的时间步长为1×10-4s,对1~5 000 Hz范围内的声波捕获较为精准.
3 物体入水噪声特性
3.1 零流速下物体入水的噪声特性
零流速工况指的是科考平台不动时物体由滑道滑入静水中.在流体域外设置24个监测点,接收点位于平面y=0上,接收点1~24逆时针分布于半径为10 m的圆周上,相邻之间的角度为15°,编号顺序见图5.接收点6为船尾方向,接收点18为船首方向,用于噪声测量.
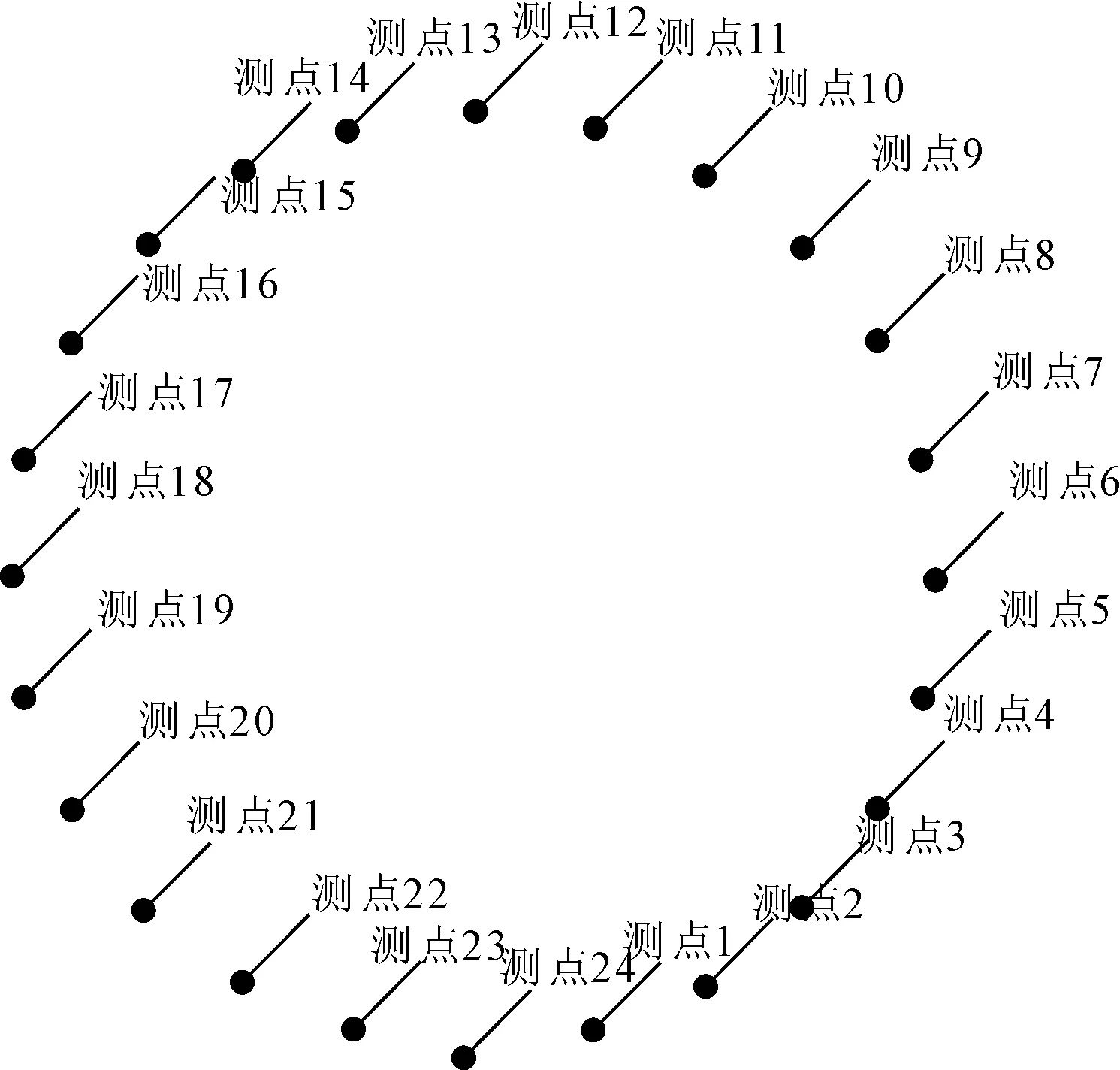
图5 监测点设置
选择入水速度3 m/s模拟滑块滑动入水,得到自由液面变化和滑块受力曲线见图6~7.由图6~7可知:滑块沿着滑道下滑的过程中,滑道液面保持水平,滑道内的液面发生明显下降,且在滑块尾部产生了空泡.从滑块的水动力载荷可以看出,随着时间的增长,滑块的受力逐渐增大,这是由于滑块在做加速运动,速度越来越大,直至滑块完全入水,只受到流体阻尼作用,受力开始减小.
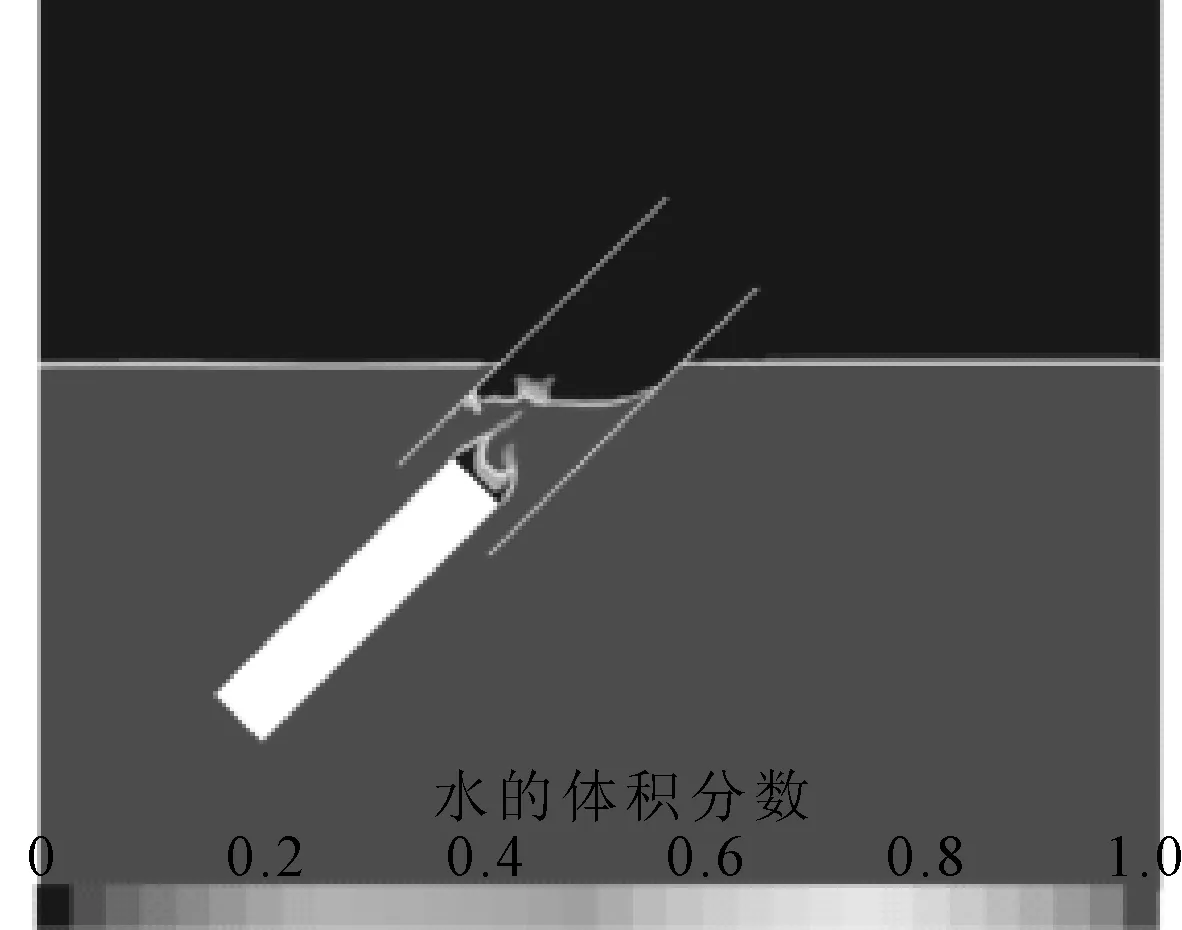
图6 自由液面

图7 水动力载荷及下沉量
待流场发展充分后,添加FW-H声学模块进行噪声计算,噪声源主要为滑块与滑道摩擦产生的机械噪声和滑块入水产生的流噪声.计算稳定后,读取监测点的声压数据,得到噪声时域曲线见图8,将声压转换成声压级,然后进行傅里叶变换,将噪声时域信号转换为频域信号,再根据噪声频域值计算1/3倍频程带级,见图9.1/3倍频程谱级是在每1/3个倍频程内,噪声的声压谱级,其中心频率f0按ISO推荐频率为(1.0 1.2 5 1.6 2.0 2.5 3.1 5 4.0 5.0 6.3 8.0) ×10 m Hz.由声压谱级计算1/3倍频程谱级为

图8 噪声时域曲线,监测点(-9.659 260-2.588 19)
(8)

总声级是指整个频带范围内的声压级,用来表征整个频带内的噪声水平,其表达式为
(9)
式中:f1、fh分别为频率范围上、下限频率.
由式(7)计算得到总声压,制成各监测点总声级见表2,再借助origin软件处理得到噪声指向性图,见图9~10.刚开始监测点压力波动很小,随时间增加压力波动逐渐增大,这是因为滑块在做加速运动,速度越来越大.由图9可知:物体入水过程的噪声能量集中于低频段,位于500~1 000 Hz,之后随着频率的增加,噪声级逐渐减小.图11为滑块的噪声指向性图,其中90°是尾部方向,270°是首部方向,可以看到科考平台左舷和右舷方向噪声较大,与潜艇噪声[9]计算得出的8子型声指向性规律类似,噪声计算结果具有可信度.
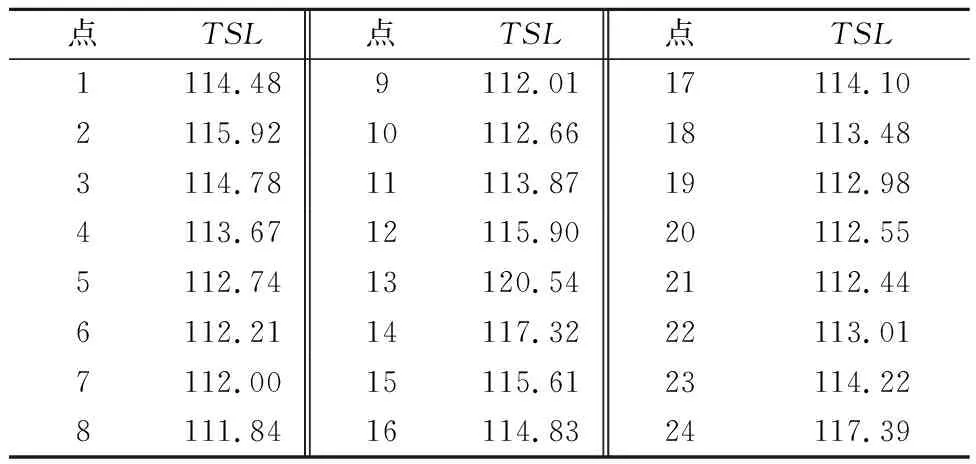
表2 监测点总声级 单位:dB

图9 噪声频域曲线
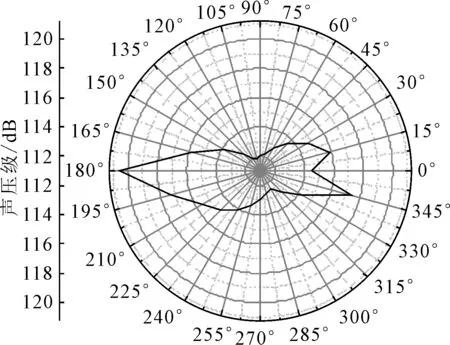
图11 噪声指向性
对物体入水噪声结果进行进一步细化处理,选择若干个典型的时刻进行分析,根据滑块的入水情况将这个过程分为:①头部到达滑道口之前(某一时刻);②头部到达滑道口时刻(特定时刻);③头部脱离滑道口,尾部还未入水(某一时刻);④尾部入水时刻(特定时刻);⑤尾部已入水,但尾部到达滑道口之前(某一时刻);⑥尾部到达滑道口(特定时刻);⑦尾部脱离滑道口后(某一时刻).计算得到不同时刻典型监测点处的噪声级见图12.头部到达滑道口之前的噪声最小,这是由于在此阶段滑块速度较小,在后面的阶段,速度较大,导致噪声较大.

图12 不同时刻典型监测点总声级
3.2 有流速时物体入水的噪声特性
有流速工况指科考平台不动时物体由滑道滑入具有一定流速的水流中,文中模拟了水流流速为0.651 m/s时物体滑动入水的过程.计算得到滑块下滑入水过程的自由液面变化和受力曲线见图13~14.由图13可知:当水流具有一定速度时,滑块滑动入水过程,滑道内自由液面明显下降,滑块尾部形成空泡,并且在滑道外气液交界处自由液面发生振荡.由图14可知:滑块运动初始会因为水流运动影响受到一个较大的力,在短时间内恢复正常,受力逐渐增大至滑块完全入水,然后受力开始减小.

图13 自由液面
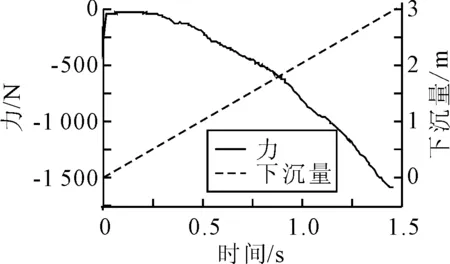
图14 水动力载荷
入水过程的典型时刻见表3,待流场发展充分后,添加FW-H声学模块进行噪声计算,监测远场中时域脉动压力,并通过傅里叶变换分析噪声频域特性和噪声指向性,结果见图15.由图15可知:模型头部完全入水和尾部刚入水时刻其脉动压力均产生较大波动,但头部完全入水导致压力增大,而尾部刚入水则是其所受压力减小.产生噪声峰值在255度左右即平台首部附近.因此,产生较大噪声和较大压力波动的首部结构需要重点考虑.

表3 运动时刻表

图15 有流速物体入水噪声结果分析
4 噪声抑制方法研究
4.1 截面面积优化
为分析滑道截面面积对物体入水噪声的影响,应当保持滑块尺寸不变,选择不同滑道尺寸进行模拟.考虑到后续实际试验的影响,文中数值模拟保持滑道尺寸不变,只改变滑块尺寸,进行滑道截面面积变化对物体入水噪声影响的等价分析.定义特征长度L=100 mm,初始工况case1滑块截面为3L×3L,创建新工况case2,其滑块截面为2.5L×2.5L,对应滑道截面为5.28L×6.72L;新工况case3,其滑块截面为2L×2L,对应滑道截面最大为6.6L×8.4L.噪声监测点设置不变,得到不同工况下典型监测点6(尾部,迎着入水物体)、12(右舷)、18(首部,远离入水物体)和24(左舷)的总声级见图16.

图16 不同工况典型监测点总声级
由图16可知:4个噪声监测点的计算结果都是中截面积(case 2)的噪声最小.这意味着对于相同尺度的入水物体,滑道存在一个噪声最低的最佳截面积.对于本文所采用的三个滑道面积,当物体尺寸统一转换为模型一(3L×3L)时,滑道截面积为case 2(5.28L×6.72L)时噪声最小,可以认为此时的滑道截面积为最佳截面积.此时,在右舷侧监测点(位置12),噪声降低最大幅值可达约9 dB.在其他监测点,最佳截面积(case 2,5.28L×6.72L)比初始截面积(case1,4.4L×5.6L)和最大截面积(case3,6.6L×8.4L)降幅约为2 dB.
4.2 空腔消除
数值仿真为无空腔的长方体模型,中间没有掏空.为分析空腔对物体滑动入水噪声的影响,创建空腔模型,将长方体模型中间掏空两个小长方体,两小长方体之间间隔100 mm,小长方体与大长方体边界距离为50 mm,空腔模型和打孔尺寸分别见图17.

图17 空腔模型示意图和打孔尺寸
比较滑道有空腔和无空腔时物体滑动入水产生噪声的指向性情况见图18.由图18可知,增加空腔虽然没有改变噪声的指向性,但噪声总声级明显降低.进一步对比典型监测点6、12、18和24有空腔和无空腔时产生噪声级的情况,见图19.由图19可知:采用平滑腔体可以有效抑制噪声,在监测点12处噪声抑制的效果最好,最大噪声降幅约为8 dB,最小噪声降幅为0.9 dB,空腔消除的噪声抑制效果平均约为3 dB.

图18 有无空腔噪声指向性对比

图19 有无空腔典型监测点总声级
5 结 束 语
文中建立了物体由滑道入水的数值模型,计算并分析了物体滑动入水时产生的噪声大小和噪声指向性情况,给出并分析了噪声抑制措施及其效果,对于完善水下噪声抑制理论体系和提高实际科考平台作业时信息收集的精确性具有重要意义.结果表明:物体由滑道滑动入水时产生的噪声能量集中在低频段;有流速噪声级普遍大于零流速噪声级,且有流速工况噪声在平台左舷和右舷方向较大,零流速工况噪声在平台首部右侧附近较大;滑道截面面积优化和增加空腔均能有效抑制物体入水产生的噪声,前者降噪最大幅值约9 dB,后者降噪最大幅值约8 dB,且最佳降噪效果均位于平台右舷方向.

