准零刚度隔振系统吸引子迁移控制优化研究

陈旭超 刁爱民 杨庆超* 柴 凯

(海军工程大学动力工程学院1) 武汉 430033) (海军工程大学舰船与海洋学院2) 武汉 430033)

0 引 言

准零刚度隔振系统在平衡位置能提供较高的静刚度和较低的动刚度，使其在低频隔振方面效果显著，在振动控制领域有着广泛的应用前景．然而，由于非线性因素的影响，系统中可能存在多个稳定的吸引子，且不同的初始条件有可能对应不同振幅的吸引子，如果没有受到扰动，系统的运动状态不会发生改变，而当初始条件改变时，系统有可能跃迁到大振幅吸引子上，影响设备的正常工作，降低设备使用寿命．

在多吸引子系统中，通过施加吸引子迁移控制可以实现不同运动状态之间的转换．迁移控制算法由最早的开环控制，发展到开环控制和线性反馈控制相结合的 (open plus closed loop，OPCL)控制[1]，并经进一步优化，实现开环加非线性闭环(open plus nonlinear closed loop，OPNCL)的控制[2]．在实际应用方面，韩清凯等[3]对OPCL控制方法进行改进，实现了连杆机构的同步运动．沈建和等[4-5]进一步验证了OPCL控制方法的全局性．赵建学等[6]利用开环加闭环的方法实现周期吸引子之间的迁移控制．柴凯等[7-8]利用OPCL控制和OPNCL控制等算法实现了周期吸引子之间、周期和混沌吸引子之间的迁移控制，并结合ADAMS仿真软件验证了OPCL控制方法的可行性．杨庆超等[9]使用OPNCL控制方法使两自由度非线性系统在不同参数下始终处于小振幅持续混沌运动，能实现隐匿线谱信息和保持隔振性能的双重功能．左兆伦等[10]将OPNCL控制算法应用于同步系统混沌吸引子控制，仿真结果显示特征线谱强度明显下降．

综上所述，针对准零刚度隔振系统多吸引子共存且振幅相差较大的特点，文中以两自由度准零刚度隔振系统为研究对象，分析了非线性系统的多吸引子共存现象以及不同吸引子对应的时间历程图和相图，对OPNCL迁移控制算法进行优化设计，实现在任意初始条件下，系统最终都能运行于振幅最小、隔振效果最好的运动状态．

1 两自由度准零刚度隔振系统动力学分析

引用如下两自由度准零刚度隔振系统的一阶形式量纲-的量动力学微分方程.

γ(x1-x2)2-(x1-x2)3+fcos (ωt)

w(x1-x2)-wγ(x1-x2)2+w(x1-x2)3

(1)

式中：x=[x1,y1,x2,y2]为状态变量；γ、f、ω、w、ξi、k2为系统参数．该系统为具有平方项和立方项的非自治耦合微分方程组，产生的输出信号取决于系统的初始状态变量．当参数取定为γ=2，w=0.5，k2=1，ω=1.6，f=6.8，ξi=0.1，i=1,2，第一组初始状态向量取(0，0，-4，0.5)和(0，0，0，0)，系统(1)经历瞬态并最终稳定于状态A，时间历程图见图1a)，取稳态后的相图见图1b)．第二组初始状态向量取(0，0，0，3)和(0，0，-2，4)，系统(1)经历瞬态后稳定于状态B，时间历程图见图2a)，显然A的振幅小于B的振幅，则记状态A为运行于小振幅吸引子上，状态B为运行于大振幅吸引子上，取稳态后的相图见图2b)．

图1 小振幅吸引子时域和相图

图2 大振幅吸引子时域和相图

由图2可知：大振幅吸引子和小振幅吸引子为两种不同的形状，小振幅吸引子类似于环状，与大振幅子吸引子明显不同．图3为不同吸引子对应的功率谱图，由图3可知：大振幅吸引子对应的功率谱比小振幅吸引子对应的功率谱大0.99 dB，显然处于小振幅吸引子更有利于设备的正常工作．

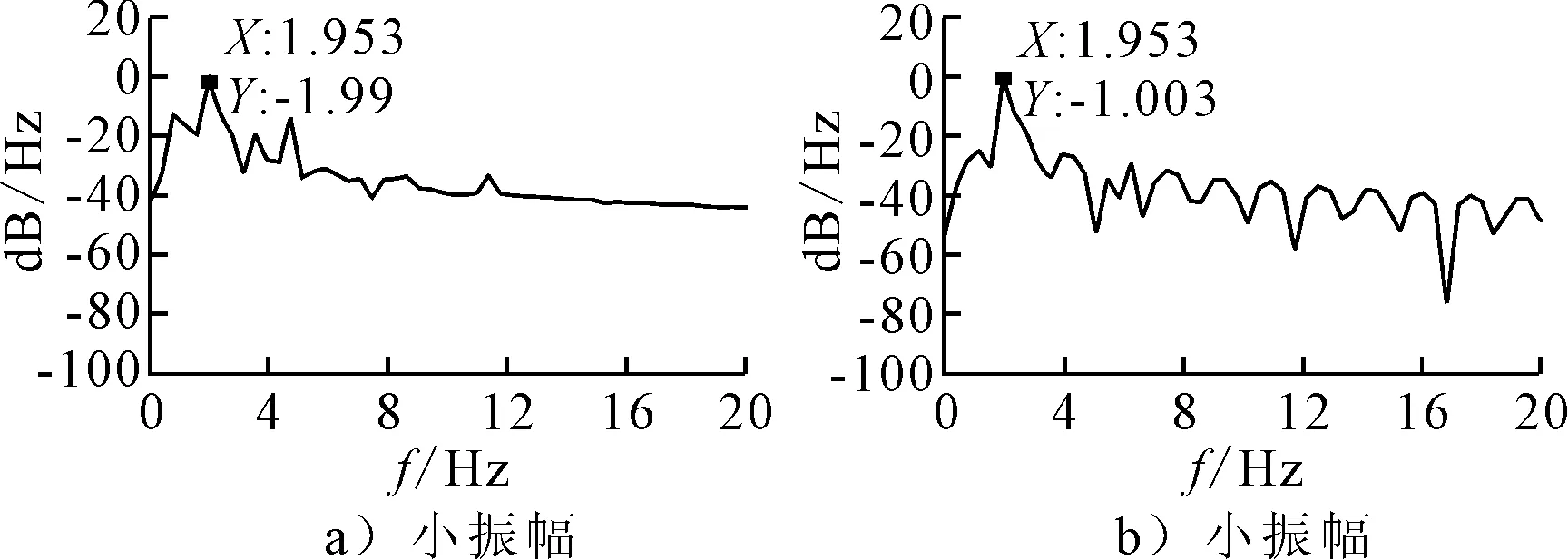
图3 不同初始条件下共存吸引子功率谱图

保留系统参数设置，设置初始条件(x1,y1)=(0,0)，以-6≤x2≤6,-10≤y2≤10为分析平面，利用胞参考点映射法得到两个共存吸引子对应的吸引域分布图，见图4．结合图1～2可知：黑色区域和红色区域分别为大振幅吸引子B和小振幅吸引子A的吸引域．在具有初值敏感性的非线性系统中，两个吸引子都有其对应的吸引域，即从同一吸引域出发的相轨迹都将渐进稳定于该点所属的吸引子，从不同吸引域出发的相轨迹将运行于不同的吸引子，说明共存吸引子具有渐进稳定性．

图4 共存吸引子吸引域分布图

2 共存吸引子迁移控制优化

2.1 迁移控制

吸引子迁移控制的基本原则是对原系统施加控制，使得受控系统的目标轨道存在局部稳定区域与共存吸引子的吸引域部分重叠，当原系统运行到重叠部分时，启动控制，这样受控系统就可沿着该稳定轨道运行[11-12]．当该轨道的起点在一个吸引子上，终点在另一个吸引子的吸引域时，则可以实现从一个吸引子到另一个吸引子的迁移控制．在两自由度准零刚度隔振系统上添加控制器U=(u1，u2，u3，u4)T，得到如下受控系统：

(2)

若将系统(1)控制到目标轨道g=(g1，g2，g3，g4)上，定义误差信号为ei=xi-gi,i=1,2,3,4．将误差变量代入受控系统(2)得到误差系统.

(3)

选用OPNCL控制算法中的控制项.

(4)

式中：

γ(g1-g3)2-(g1-g3)3+fcos(ωt)

wξ1(g2-g4)+w(g1-g3)-

wγ(g1-g3)2+w(g1-g3)3

(5)

(6)

(7)

其中：Δ1=g1-g3，Δ2=e1-e3．

2.2 迁移控制优化

(8)

式中：ε为实数．控制流程图见图5．

图5 优化后的迁移控制系统结构

3 数值仿真

设置激励力幅值为6.8，取ε=0.6，目标函数g1=g3=1.5+sin(0.5t)，g2=g4=0.5cos(0.5t)，输入初始条件xp=[0,0,-1.98,-6.5]，基座的相轨迹和时间历程图见图6．由图6可知：系统经历瞬态并最终运行于小振幅吸引子．输入初始条件xp=[0,0,-1.02,3.1]，基座的相轨迹和时间历程图见图7．由图7可知：系统刚开始运行于大振幅吸引子，当系统运行至大振幅吸引子与目标轨道g(t)邻域的重叠区域时启动了迁移控制，系统迅速迁移至目标轨道g(t)或g(t)的邻域；当系统运行至目标轨道g(t)邻域与小振幅吸引子对应吸引域的重叠区域时，关闭控制，系统逐渐迁移并最终稳定运行于小振幅吸引子．由第二节所述胞映射的分析结果可知两个初始条件分别对应不同的吸引子，验证了仿真结果的正确性．

图6 xp=[0,0,-1.98,-6.5]时基座的相轨迹和时间历程图

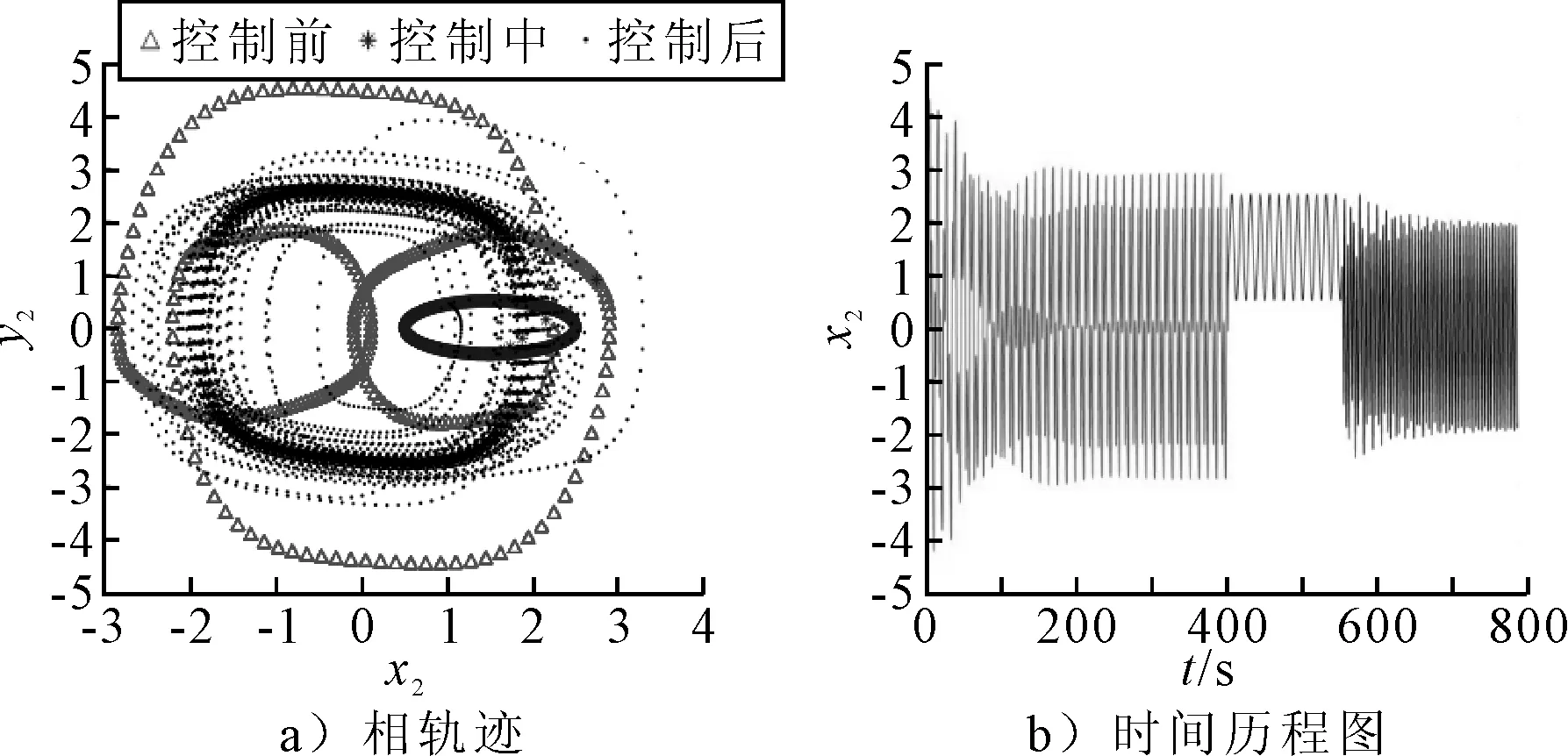
图7 xp=[0,0,-1.02,3.1]时基座的相轨迹和时间历程图

在胞映射分析平面之外取点，输入初始条件xp=[0,0,-10,-10]，取稳态之后基座的相轨迹见图8a)．由图8a)可知：系统始终运行于小振幅吸引子．输入初始条件xp=[0,0,-10,-5]，基座的相轨迹见图8b)．由图8b)可知：系统刚开始运行于大振幅吸引子，但是经过自适应控制之后最终稳定运行于小振幅吸引子．

对比以上结果可知系统从大振幅吸引子自动迁移到了小振幅子吸引子上，系统的振幅降低，达到了小振幅吸引子自适应迁移控制的目的．此外，在迁移过程结束后，控制函数s为0，意味着不需要持续施加控制能量，满足实际工程应用中的低能耗需求．

4 结 论

1) 两自由度准零刚度隔振系统存在多吸引子共存的现象，初始条件的改变会使系统由小振幅吸引子迁移到大振幅吸引子上．

2) 优化后的迁移控制方法能够在任意初始条件下使系统最终稳定在小振幅吸引子上，从而降低基座的振幅，提升隔振性能，并且该方法具有稳定性强、能耗低的特点．